绳结涡旋对绳索抗拉性能的影响

王哲 , ，赵海涛，刘扬，陈吉安

（1.上海交通大学 航空航天学院，上海 200240；2.上海航天技术研究院 上海宇航系统工程研究所, 上海 201109）

聚对苯撑苯并双噁唑（PBO）绳索自20 世纪80 年代以来，其优异的性能使其得到迅速发展和广泛应用。航空、航天等高端领域对绳索的需求越来越迫切，而对绳索打结的研究却非常少，但计算机仿真分析对研究PBO 绳索打结的力学性能提供了有力的支持。

PBO 纤维是一种高性能有机纤维，许多学者对其展开了研究。刘姝瑞等通过实验测试了PBO 纤维紫外性能、耐酸碱性等性能，并观察了纤维表面形态的变化[1]。王宁等研究了PBO 纤维抗紫外老化改性，根据抗紫外线整理剂与PBO 纤维不同的结合方式，将其抗紫外改性方法分类，总结了各种方法的特征和优缺点[2]。赵婷玉等研究了PBO 纤维增强有机硅压敏胶的制备，并采用射线辐照的方法对其性能进行了研究，结果表明辐照原位改性可以提升压敏胶的耐热性和高低温力学性能[3]。 Zhang 等从PBO 纤维分布情况方面对纤维束强度进行了研究，假设单根纤维强度的分布函数符合矩形分布或正态分布，预测了纤维束的断裂过程，还利用威布尔分布对PBO 纤维束的断裂过程进行了预测，并与矩形分布和正态分布进行了比较[4]。刘亦冰等研究了3 种不同PBO 纤维在不同高温处理后力学性能的变化，得到了PBO-HM 纤维的力学稳定性更好的结论[5]。陆瑶等开展了PAN 纳米纤维膜对 PBO 织物影响的研究，采用静电纺丝的方法，结合实验分析发现表面覆膜可提高 PBO 纤维增强复合材料的层间剪切强度[6]。王虹等采用扫描电镜对PBO 纤维增强复合材料展开研究，测试了导热系数、氧指数等指标，得出的复合材料兼具了 PBO 纤维毡和气凝胶二者的优异特性[7]。

绳索打结的力学分析也取得了不错的进展。刘香园等就绳结打法展开研究，运用MATLAB 软件，主要构建了绳结交叉点数与其松脱时所承受负荷大小的拟合模型，得出了绳结半径越大，其结点处的极限强度越强，半径越小，结点处的极限强度越小的结论[8]。吴昊等采用Verlet 法数值求解模型动力学方程，提出一种基于层次包围球的模拟受力方法，增加了缝合线运动模拟的逼真度和实时性，提高了仿真效率[9]。Qwam 等对不同的拓扑结构的手术结展开研究，进行了绳结拉伸实验，并通过仿真模拟的方法验证了其力学性能[10]。Baek 等提出了一种利用几何非线性、全三维仿真分析来模拟弹性杆中结的方法，考虑了完整的三维变形得出紧弹性结的三维变形是其力学响应的核心[11]。赵文锐等研究了纱线不同结头形式打结拓扑结构的稳定性，经对比分析，得出盘头结的断裂强力较高，适合在生产中使用[12]。Jawed 等通过实验和理论结合的方式，研究了长横向弹性结的摩擦响应，建立了一个基于薄弹性棒非线性理论的解析模型[13]。狄剑锋分析了转杯纺纱接头打结关键技术，并且研究了自动接头工艺的关键技术[14]。朱阳就绳结能量展开分析，针对拎手绳打结进行研究，利用悬链线理论建立拎手绳的二维数学模型，得到了能量越小绳子就越趋于稳定，打结成功率越高的结论[15]。

综上，国内外均有学者对PBO 纤维性能进行研究，但对PBO 纤维绳结的抗拉性能的研究较少。绳结方面，国内学者没有对绳结结构进行深入研究，国外学者研究的绳结较为细致，但均为单根绳索所形成的绳结。本文深入绳结结构，从绳结涡旋方面对两根绳索对接而成的绳结展开研究，通过绳结拉伸实验，探究了绳结涡旋对绳结抗拉性能的影响，提出了一种新的评估绳结抗拉性能的方法，能根据涡旋的数量和绳结的等效长度，实现各种绳结的抗拉性能的评估。

1 绳索和绳结

1.1 实际绳索尺寸测量

本文采用的绳索是由PBO 纤维编织而成，且绳索中无基体材料。PBO 纤维是一种高性能有机纤维，绳索横截面近似为圆形。为了便于建立绳结模型，假设绳索的横截面为圆形，本文采用直径d为3.1 mm 的绳索，如图1 所示。

图1 绳索直径示意图Fig.1 Diameter of a rope

1.2 绳结的等效长度

绳结的等效长度是指绳结部分所占用绳索的长度。同等粗细绳索的不同绳结占用的绳索长度不同，本节采用了多根相同的PBO 绳索，每两根绳索打一个绳结，研究了金钱结、渔夫结、外科结和飞艇结这4 种绳结，照片如图2 所示。

图2 各绳结照片Fig.2 Various rope knots

对不同绳结施加拉力，随着拉力的增大，绳结逐渐变小至基本不变。当绳结并未拉断且收紧形成体积无明显变小的稳定状态后，切去绳结之外的绳索部分，然后解开绳结，测量绳结所占用的绳索的长度（用L表示），每种绳结取3 个试件测量3 次，取平均值，测量结果如表1 所示。

表1 各绳结的等效长度Tab.1 Equivolent lengths of various rope knots

2 绳结和绳索拉伸实验

不同的绳结能承受的最大拉伸载荷不同，根据绳结的用途不同可以把绳结分为固定绳结、接绳绳结、保护绳结和操作绳结等类型。本节研究两根绳索进行对接的接绳绳结。

2.1 绳结拉伸实验

对于不同种类的绳结，绳结中受力情况均十分复杂，从直观上去判断其抗拉性能较为困难，对多组不同的绳结做缠绕式拉伸实验，实验仪器为SUNS单轴拉伸试验机及缠绕式夹具，如图3 所示。将绳索的下端缠绕在固定不动的拉伸机上，上端与拉伸机夹具连接，拉伸时随夹具向上运动，受到的拉力逐渐增大，直到绳结被拉断，拉伸机实时记录此拉力的变化过程。

图3 SUNS 单轴拉伸试验机及缠绕式夹具Fig.3 SUNS single-axial tensile experiment device

在以上绳结拉伸实验过程中，采用了高速摄像机，拍摄了各绳结的拉断过程，拍摄结果如图4所示。

图4 高速摄像机记录的各绳结断裂结果Fig.4 Rope knot breakage results recorded by high-speed video camera

通过用高速摄像机来精确定位打结的宏观断裂的位置。在加载过程中，绳结大小先不断缩小，然后基本不变，直至断裂。在拉伸过程中，绳结绕着拉伸方向缓慢自转，该自转现象是绳结中涡旋的复杂作用过程的综合效应产生的。每种绳结都重复3 次实验，实验结果如图5 所示。

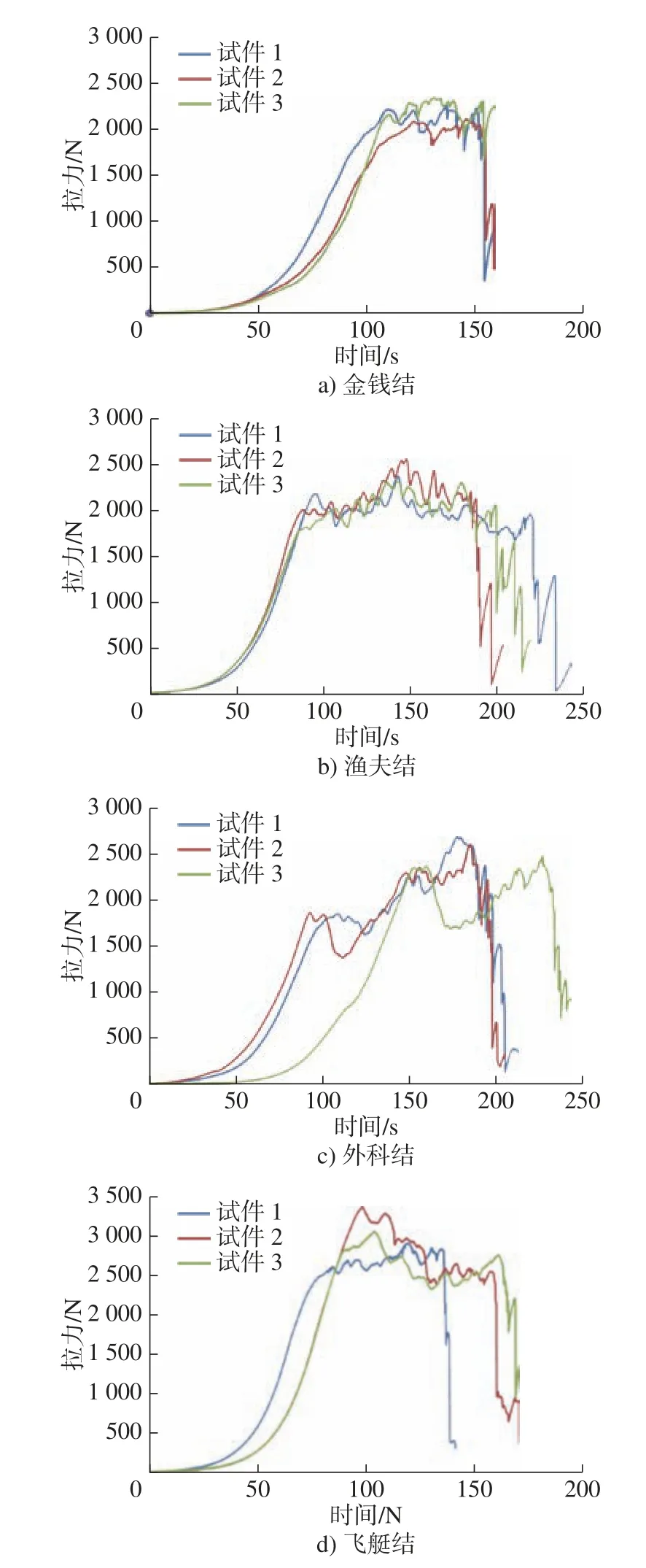
图5 绳结拉伸实验结果Fig.5 Knot tensile test results

本节实验结果中，绳结拉伸实验获得的各绳结能承受的最大拉力，将各绳结得到的实验结果求平均值，如表2 所示。

表2 绳结能承受的最大拉力实验结果Tab.2 Maximum tensile forces bearable by rope knots

从表2 可以看出：根据承受的最大拉力从小到大给绳结排序依次为：金钱结 ＜ 渔夫结 ＜ 外科结 ＜飞艇结。

打结对绳索抗拉性能的影响因素包括拉伸载荷和绳结中的摩擦。以金钱结拉伸实验为例，绳结随着拉力逐渐增大、绳结逐渐破坏的过程如图6 所示。

图6 金钱结的拉伸实验过程Fig.6 Tensile experimental process of the money knot

图6a）和图6b）阶段：绳结明显在缩小，由于纤维材料抗拉却不耐磨，破坏形式主要是绳结内绳索的外围纤维相互摩擦而破坏，原本在绳结中的一部分绳索被拉到绳结外，此部分被拉出来的绳索由于外围纤维已磨损，所以比完好的绳索更细、抗拉性能更弱。

图6c）和图6d）阶段：绳结缩小逐渐减缓，此时既存在绳结内纤维的磨损，也存在绳结外纤维的拉断，绳结外的绳索进一步变细，破坏形式逐渐偏向于绳结外的绳索纤维的拉断。

图6e）和图6f）阶段：绳结大小基本不变，由于绳结外的绳索已经很细，此时破坏形式主要是绳结外的纤维被拉断，直至被完全拉断。

2.2 绳索拉伸实验

为了分析打结对绳索抗拉性能的影响，需要对未打结的绳索进行研究。采用与2.1 节相同的绳索、实验装置和方法，通过拉伸实验测量未打结的绳索能承受的最大拉力，选取3 根相同的PBO 绳索做与2.1 节相同的缠绕式拉伸实验，同样采用SUNS 单轴拉伸试验机及缠绕式夹具，重复3 组实验，将得到的实验结果求平均值，如表3 所示。

表3 绳索的拉伸实验结果Tab.3 Tensile forces of rope knots

未打结绳索的拉伸实验结果表明其能够承受的最大拉力平均值为16 439.833 N。绳结和未打结绳索拉伸实验采用的绳索相同，从打结绳索和未打结绳索的实验结果表明，绳结大大减低了绳索能够承受的最大拉力。用两根绳索打了一个绳结后，由于绳结涡旋位置的缠绕相互摩擦，将使绳结位置成为整根绳子的一个薄弱点。

3 涡旋对绳结抗拉性能的影响

影响绳结抗拉性能的因素有许多，摩擦是影响因素之一，由于摩擦主要存在于绳结涡旋处，从而可以研究绳结涡旋来评估绳结的抗拉性能，本节研究绳结的涡旋对绳结抗拉性能的影响，不同绳结的涡旋数不同，绳结复杂程度与涡旋数量有一定的关系，且在拉伸过程中，绳结不断缩小，在收缩到一定程度之后大小基本不变，所以绳结抗拉性能与绳结涡旋和绳结的等效长度有关。

3.1 绳结模型

本节采用UG 建立了各绳结模型，首先建立绳结模型的中心线轨迹，假设绳索横截面为圆形，采用第一节对绳索直径的测量结果，然后对中心线轨迹使用“管”命令，得到绳结模型，如图7 所示。

图7 各绳结模型Fig.7 Models of each knot

3.2 绳结的涡旋

绳结中绳索会围成数个空白区域，当绳结两端受到拉力时，绳索各部分都会运动，用箭头表示绳索的运动方向，以金钱结为例，当围成某个空白区域的绳索的运动方向可以组成一个顺时针或者逆时针的循环，则称此空白区域为一个涡旋，如图8 所示。金钱结中共有7 个空白区，而中间空白区的周围绳索的箭头方向正好组成一个顺时针的循环，则该空白区为一个涡旋，该涡旋由4 条边围成，绳结涡旋的总边数为4。

图8 金钱结涡旋示意图Fig.8 Schematic diagram of the money knot vortex

3.3 抗拉性能的影响评估

当绳结两端受到拉力时，如图9 所示，拉力与蓝色椭圆虚线中的绳结部分的绳索之间的摩擦力的合力平衡，根据库仑摩擦定律：摩擦力跟作用在摩擦面上的挤压力成正比，跟外表的接触面积无关。

图9 绳结两端受拉力示意图Fig.9 Schematic diagram of tension at both ends of knot

采用相同粗细绳索的绳结，绳结越小说明绳结收缩越紧，绳结中的挤压力则越大，绳索之间的摩擦力更大，从而使得绳结能够承受的拉力越大。而绳结的紧凑程度可以用平均每个涡旋的每个边所占用的绳索长度来评估，所占用的长度越短，则说明绳结越紧凑。

涡旋中绳索相互切向滑动，绳索之间相互摩擦，能促进绳结收缩，从而形成更加紧凑的结构，绳结更加紧凑则能够承受的摩擦力更大，一定程度上能提高绳结的抗拉性能。为了说明绳结涡旋评估法，选取了金钱结、渔夫结、外科结、飞艇结作为研究对象，各绳结涡旋如图10 所示。

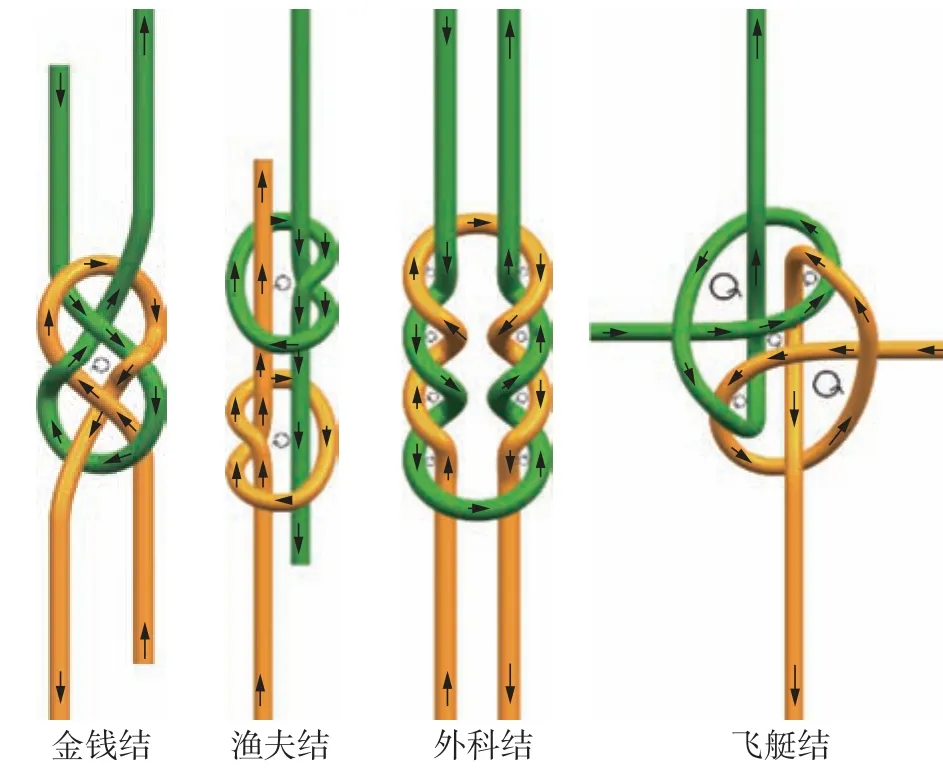
图10 各绳结涡旋示意图Fig.10 Schematic diagram of each knot vortex

绳结的涡旋总数用n表示，而各涡旋由多条边围成，其总边数用N表示。引入绳结的等效长度与涡旋总边数的比值作为评估参数，表示平均每个涡旋的每个边所占用的绳索长度，该值越小说明绳结收缩得越紧凑。各绳结的涡旋统计结果以及实验获得最大拉力的平均值如表4 所示。

表4 各绳结涡旋评估结果Tab.4 Evaluating vortices of rope knots

从表4 中可以看出：等效长度与总边数的比值越小，绳结抗拉性能越好。因为等效长度与总边数的比值越小说明绳结越紧，绳结受摩擦力相对会更大，使得绳结的抗拉性能更好。

4 涡旋判定方法的验证

本节以金钱结为例，验证涡旋的评估方法的有效性，首先对金钱结进行改进，如图11 所示，改进前为α-金钱结，绳结A、B 两端受拉；改进后为β-金钱结，绳结C、D 两端受拉，使绳结中涡旋数和总边数增多，得出了两种金钱结。

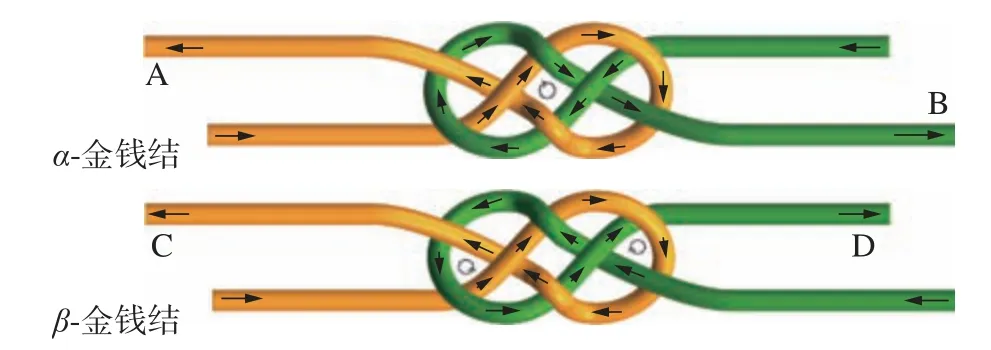
图11 两种金钱结模型Fig.11 Two golden rope knot models

对两种金钱结做拉伸实验，每种绳结取3 个试件做实验，然后对实验结果求平均值，获得能够承受的最大拉力的实验结果如表5 所示。

表5 两种金钱结的拉伸实验结果Tab.5 Tensile results of two types of money knots

对两种金钱结进行涡旋评估，验证绳结涡旋评估方法的有效性，评估结果和能够实验承受的最大拉力的平均值如表6 所示。

表6 两种金钱结的评估Tab.6 Evaluating two golden rope knots

通过以上实验验证结果可以看出，β-金钱结比α-金钱结的等效长度与总边数的比值更小、抗拉性能更好，说明了涡旋判断绳结抗拉性能的方法的有效性，验证了评估法可用于改良绳结抗拉性能的可行性。

5 总结

本文研究PBO 绳索和绳结，通过绳结拉伸实验和未打结绳索拉伸实验对比得出，发现绳索打结会极大降低绳索抗拉性能。

绳结受力非常复杂，但绳结受拉时绕着拉伸方向缓慢自转是绳结中的涡旋作用的综合效应，导致绳结各部分受力不均从而抗拉性能降低，因为绳结是在涡旋处收紧并缩小，所以绳结受摩擦力的大小与涡旋处的紧凑程度有关；然后从涡旋的角度深入研究，结合绳结的等效长度，提出了一种评估绳结抗拉能力的方法，该方法能根据绳结等效长度和涡旋的总边数的比值，实现对各种绳结的抗拉性能的评估，也可用于改良绳结抗拉性能，也为新绳结的设计及评估提供参考。