应力-强度干涉模型下的滚动轴承可靠性评估与设计方法
李燕科,邱明 , ,李军星,牛凯岑,许艳雷
(1.河南科技大学 机电工程学院,河南 洛阳 471003;2.河南科技大学 机械装备先进制造河南省协同创新中心,河南 洛阳 471003)
滚动轴承广泛应用于旋转机械中,是决定机械设备安全可靠运行的关键部件之一,一旦发生失效,设备无法正常工作,甚至会造成巨大的经济损失和人员伤亡。对滚动轴承进行可靠性设计,对于保证机械设备安全可靠运行、提高设备的生产效率具有重要的意义[1-2]。
应力-强度干涉模型是根据应力分布和强度分布的干涉程度来确定可靠性的方法,基于应力强度干涉模型的设计方法是可靠性设计中的常用方法[3]。唐继秋等[4]将应力-强度干涉模型应用在电子产品高温工作的的裕度分析当中。根据产品的可靠度要求,结合安全系数分布曲线来调整高温工作裕度值,有效地指导高温试验中所发现的故障整改范围,实现高温裕度值的定量计算。伊枭剑等[5]提出了基于应力-强度干涉模型的火工品可靠性设计方法。将可靠性指标通过应力-强度干涉模型转换为火工品感度分布参数,通过感度分布参数的合理取值实现火工品发火可靠性与安全可靠性的兼容设计。Zhang 等[6]针对隧道掘进机主传动系统的关键部件TBM 主轴承。基于应力-强度干涉模型,研究了滚子-滚道接触残余强度,考虑了材料的非线性强度退化和弥散,计算了主轴承结构的可靠性。
可靠性指产品在运动或振动状况下的可靠性,强调机械产品中所包含的特性由于机械产品的特性及参数具有固有的随机性,同时机械产品运行是典型的过程,载荷、工况、应力等工作环境及参数都是随时间变化的随机变量,必须将其处理为随机过程[7]。曹汝男等[8]等结合Kriging 模型和Monte Carlo方法提出一种可靠性分析方法AK-MCS-T。拥有拟静态法计算量小的优点又可以给出失效概率随时间变化情况。高宁等[9]利用有限差分法和有限元法相结合对航空齿轮泵弹流润滑数学模型进行耦合求解。采用重要抽样法与自适应 Kriging 相结合的AK-IS 方法进行了航空齿轮泵滑动轴承的可靠性和可靠性灵敏度分析,研究高转速、低介质粘度运行的航空齿轮泵滑动轴承动压润滑可靠性。Wang 等[10]提出了一种基于PID 控制器的振动主动控制系统风险评估的区间可靠性计算方法。Zhang 等[11]求解了经典的滚动轴承系统的随机动力学方程,并对滚子定位精度的可靠性进行了检验。刘国[12]以实际工作过程中的可靠度为约束条件,针对试验得出的无失效数据,改变贝叶斯估计的先验分布区间大小,进行传统贝叶斯可靠性估计,为火车轴承的可靠性预测提供理论参考。王瑞祥等[13]针对小样本无失效寿命试验数据,基于Bayes 理论建立可靠性评估模型,有效提高了小样本无失效数据可靠性评估精度。高攀东等[14]在对轴承寿命分布进行分析的基础上,根据多层Bayes 法,研究了无失效可靠性试验中的试验分组问题,通过对比分析给出了较适合于航空轴承无失效数据分析时超先验分布中参数c的参数值。
利用威布尔比例风险模型(WPHM),通过提取轴承全寿命周期数据的时域、频域和时频域特征,Wang 等[15]提出了一种基于核主成分分析(KPCA)和威布尔比例风险模型(WPHM)的滚动轴承可靠性评估方法。刘晓飞[16]提出基于威布尔比例故障率模型和长短期记忆网络(Long short-term memory,LSTM)的滚动轴承可靠性评估及预测方法。刘璐等[17]提出了一种基于局部切空间排列(LTSA)和威布尔比例故障率模型(WPHM)的滚动轴承可靠性评估方法。叶亮等[18]提出用振动瞬时值的波动范围、振动平均值的波动范围、振动序列对应时间段内的平均波动范围3 个指标来综合表征在轴承服役过程中其振动性能的不确定性,并定量分析3 个不确定性指标与振动性能保持可靠性的内在具体关系。运用最大熵法和泊松过程理论,计算轴承的振动性能保持可靠度。许凌天等[19]针对部分数据缺失的小样本无失效轴承试验问题,通过数据模拟法和Bootstrap自助法处理样本退化量,根据基于性能退化轨迹的补充信息方法进行可靠性评估。陈潇贤[20]针对轴承从正常到失效的退化过程是一个缓变趋势特性,提出利用长相关模型——广义柯西(GC)过程模型进行轴承的剩余使用寿命(RUL)预测。推导出GC 过程的随机微分方程,建立了基于GC 过程的退化模型,并采用极大似然法来估计模型中的参数。确定的模型在规定阈值下求出模型在当前时刻的概率密度函数(PDF)用于预测剩余使用寿命(RUL)。
基于上述情况,只有极少研究考虑实际工况及轴承的动力学行为对轴承寿命与可靠性的影响。本文提出一种应力-强度干涉模型下的滚动轴承可靠性评估与设计方法,考虑轴承的动力学行为,将载荷处理为随机过程,基于应力-强度干涉模型,将可靠性指标转化为滚动轴承当量动载荷许用范围,再根据当量动载荷许用范围的合理取值,结合轴承设计公式,对轴承参数进行优化,从而使轴承满足该工况下目标寿命和目标可靠度。最后,通过寿命仿真,对本文方法进行验证和对比分析。
1 滚动轴承可靠性评估与设计模型
1.1 应力强度干涉理论
应力-强度干涉模型是根据应力分布和强度分布的干涉程度来确定可靠性的方法,是一种常见的机械可靠性设计方法。本文将它引入到滚动轴承可靠性设计当中。滚动轴承对应可靠寿命下的当量动载荷是随机的,外部施加载荷也是随机的。滚动轴承能否满足对应可靠度下的寿命取决于轴承当量动载荷的计算值和外部施加载荷所合成的当量动载荷的相互作用。
假设:1) 外部施加载荷所合成的当量动载荷X的概率密度函数为f(x);2)滚动轴承对应可靠寿命下的当量动载荷Y的概率密度函数为g(y);3)X和Y相互独立。根据应力-强度干涉模型的性质,X<Y的概率为滚动轴承可以满足对应可靠性寿命,用R表示,则
对应的计算式为
式(3)为采用应力-强度干涉模型计算滚动轴承满足对应可靠性寿命的一般公式,其中X和Y服从不同分布时可推导出不同的计算公式。
同理,可以得到采用应力-强度干涉模型计算滚动轴承无法满足对应可靠性寿命的一般公式为
1.2 轴承可靠性评估与设计模型
外部施加载荷和当量动载荷都是随机变量,二者都服从一定的分布。外界施加载荷服从的分布,可通过影响因素分析和试验测试数据的拟合得到,一般服从正态分布、对数正态分布。而当量动载荷一般服从正态分布、对数正态分布和对数逻辑分布等。本文对“外部施加载荷-当量动载荷”对应分布分别为对数正态分布-对数正态分布情形下的可靠性评估与设计方法进行了推导。
从式(2)和式(3)可知,如果知道外部施加载荷所合成的当量动载荷X和滚动轴承对应可靠性寿命下的当量动载荷Y的分布,就可以计算相应的可靠度。而对滚动轴承的可靠性设计则是一个逆推的过程,先给出希望达到的目标可靠度和目标寿命,再根据式(2)和式(3)来确定轴承的额定动载荷,进而对轴承参数进行优化。
外部施加载荷所合成的当量动载荷X和滚动轴承对应可靠寿命下的当量动载荷Y都是随机变量,一般都服从正态分布、对数正态分布等。本文对对数正态分布下的滚动轴承可靠性评估与设计方法进行了推导。
假设实际工况的外部施加载荷所合成的当量动载荷X服从对数正态分布ln(µx1,) , µx1和σx1分别是X的对数均值和对数标准差;滚动轴承对应可靠寿命下的当量动载荷Y服从对数正态分布ln(µy1,) , µy1和σy1分别是Y的对数均值和对数标准差;可靠度Rf, µx1和σx1已知, µy1和 σy1未知。
则由式(1)可得
由式(4)可得
式中uRf为Rf标准正态分位数。
令变差系数为k,则根据对数正态分布变差系数的定义可得
把滚动轴承对应可靠性寿命下的当量动载荷Y分布的对数值 µy1和 σy1转化为非对数值,则可得滚动轴承可靠性评估与设计的当量动载荷许用上限为
对于滚动轴承可靠性设计来说,滚动轴承无法满足对应可靠性寿命的公式为
假设滚动轴承无法满足对应可靠性寿命时,实际工况的外部施加载荷所合成的当量动载荷X服从对数正态分布ln(µx2,),滚动轴承对应可靠性寿命下的当量动载荷Y服从对数正态分布ln(µy2,),无法满足对应可靠性寿命的可靠度Rs, µx2和σx2已知,µy2和σy2未知,变差系数同样设为k。同理可得,滚动轴承可靠性评估与设计的当量动载荷许用下限为
式中uRs为Rs标准正态分位数。
基于应力-强度干涉模型进行滚动轴承可靠性评估与设计,根据计算出的当量动载荷的波动区间(µys,µyf),结合轴承寿命公式可以对滚动轴承进行可靠性评估,选取区间中值为当量动载荷的计算值,可以得到轴承在该工况下的可靠性寿命;同理,考虑可靠性寿命的满足与否,令滚动轴承可靠性设计的当量动载荷 µy满足:µys<µy<µyf,取(µys,µyf)区间中值作为当量动载荷设计均值,使滚动轴承在满足该工况下的目标可靠度寿命的同时不会溢出过多的轴承性能。
2 轴承可靠性评估与设计
轴承可靠性设计基于应力-强度干涉模型,利用对数正态分布处理轴承施加载荷范围,结合轴承设计公式可以实现对轴承的可靠性评估与可靠性设计。可靠性评估可以评估轴承在当前工况下的可靠性寿命。可靠性设计可以对轴承进行参数优化,使轴承满足该工况下目标可靠度寿命。
滚动轴承可靠性评估流程如图1 所示。

图1 滚动轴承可靠性评估流程图Fig.1 Flow chart of rolling bearing reliability evaluation
2.1 可靠性评估
根据对数正态分布下的轴承可靠性评估与设计模型,输入轴承实际工况下所承受的载荷范围,根据式(7)和式(9)可以计算出当量动载荷的波动区间(µys,µyf)。在保持较高裕度的同时,利用(µys,µyf)区间中值作为当量动载荷的计算值,利用轴承寿命公式可以对滚动轴承进行可靠性评估,得到轴承在该工况下的可靠性寿命。轴承寿命公式为
式中Ln为目标寿命。
当可靠度为0.9 时,即寿命公式L10为
2.2 可靠性设计
可靠性评估可以对实际工作中的滚动轴承计算可靠性寿命,选择更加安全可靠的轴承进行工作。同理,根据对数正态分布下的轴承可靠性评估与设计模型,可以依据目标可靠度和目标寿命对滚动轴承进行可靠性设计,具体步骤如下:
1)对进行可靠性设计的轴承,根据目标寿命Ln,目标可靠度S,额定动载荷Cr,利用式(10)可计算出当量动载荷P0。
2)对实际工况下轴承施加的载荷范围,根据对数正态分布下的轴承可靠性评估与设计模型的式(7)和式(9),计算得到当量动载荷许用范围(µys,µyf)。
3)取当量动载荷许用范围(µys,µyf)的中值P1对滚动轴承进行可靠性设计。将目标寿命Ln,目标可靠度S,当量动载荷许用范围中值P1,代入式(10),计算出可以满足当前工况下目标可靠度寿命的轴承额定动载荷Cr1。
4)比较滚动轴承原有的额定动载荷Cr与新设计的额定动载荷Cr1,根据滚动轴承额定动载荷的与轴承参数的公式,对接触角,滚动体个数,滚动体球径,内外圈沟曲率系数等轴承相关参数进行多决策变量优化,使优化后的轴承可以在该工况下满足目标可靠性寿命,以此来达到对滚动轴承进行可靠性设计的目的。
滚动轴承可靠性设计流程如图2 所示。
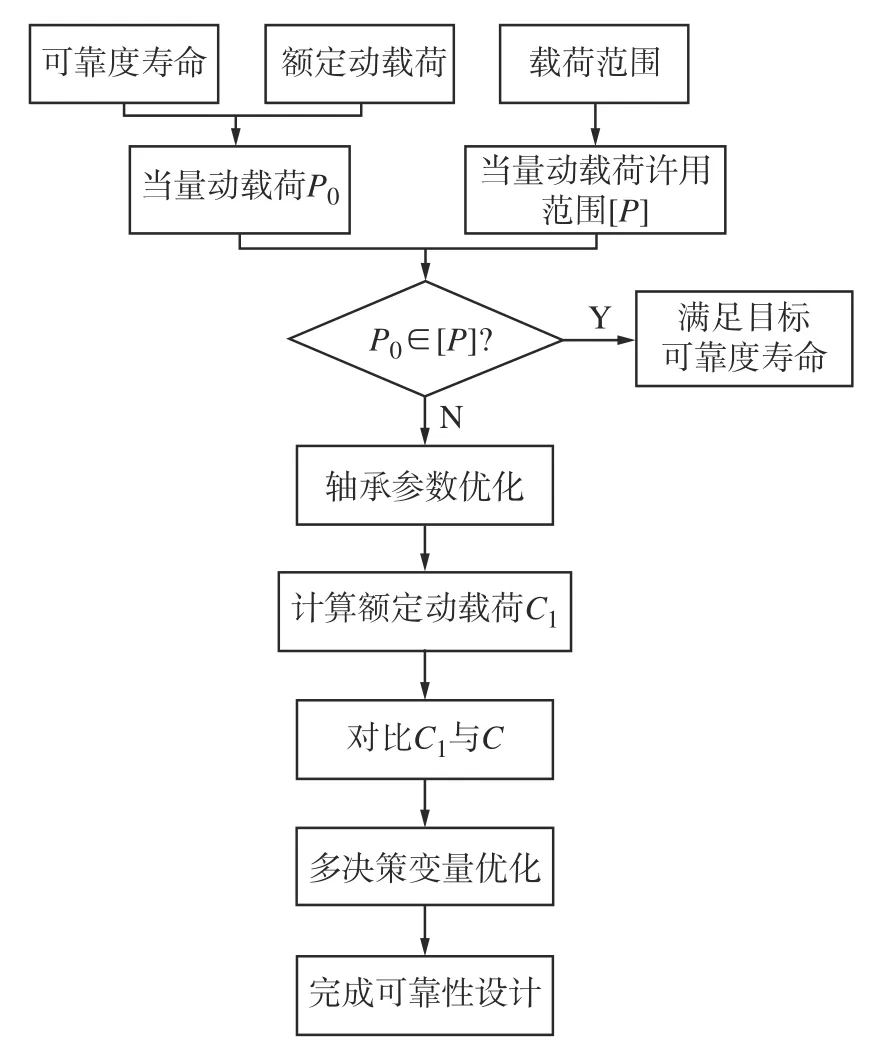
图2 滚动轴承可靠性设计流程图Fig.2 Flow chart of rolling bearing reliability design
3 仿真验证分析
3.1 滚动轴承型号和工况的选取
利用Romax 建立滚动轴承仿真模型,选取6 类深沟球轴承和7 类角接触球轴承进行仿真,具体型号如表1 所示。

表1 滚动轴承仿真型号Tab.1 Rolling bearing simulation model numbers
对表1 的6 种不同型号的的滚动轴承,每种滚动轴承在3 种工况条件下进行仿真,工况如表2 所示。
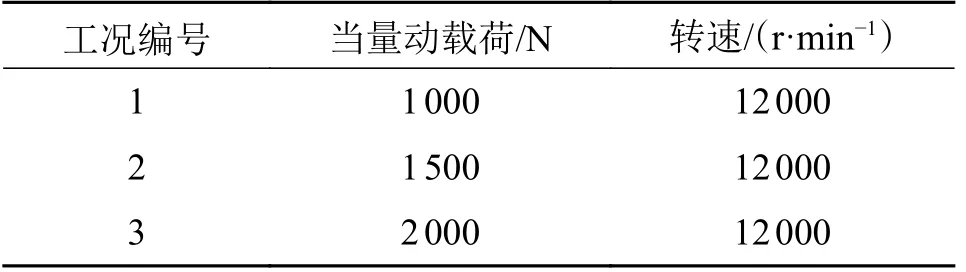
表2 滚动轴承仿真工况Tab.2 Rolling bearing simulation working conditions
3.2 仿真结果
6 类深沟球轴承,所施加的径向载荷就是轴承的当量动载荷。对3 种深沟球轴承进行3 种工况条件下的仿真,所得仿真寿命如表3 所示。
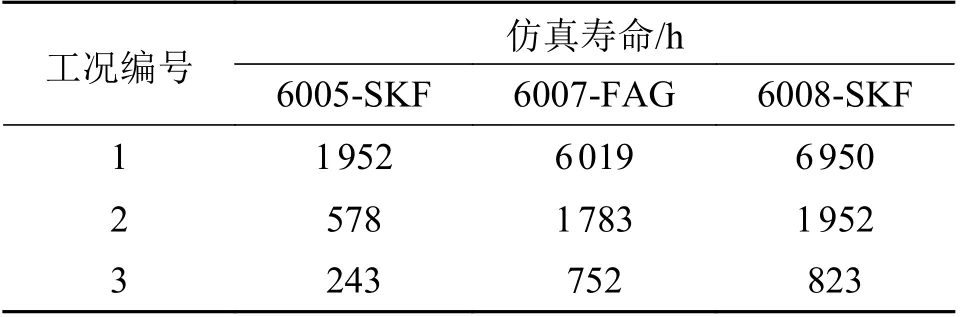
表3 深沟球轴承仿真寿命Tab.3 Deep groove ball bearing simulation life
7 类角接触球轴承,可以承受轴向力和径向力,轴承的当量动载荷由轴向载荷、径向载荷和接触角计算可得,公式为
式中:fp为载荷系数;k1为径向载荷系数;k2为轴向载荷系数。
对3 种角接触球轴承施加不同的轴向载荷,使轴承所承受的当量动载荷与工况1 ~ 工况3 中当量动载荷保持一致,轴向载荷大小如表4 所示。
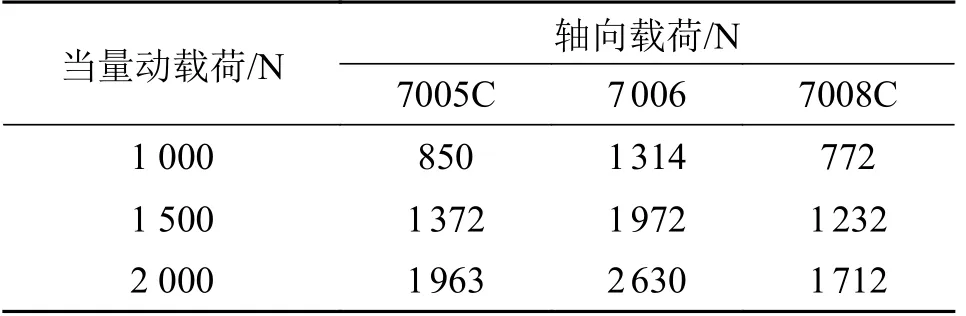
表4 角接触球轴承仿真载荷Tab.4 Angular contact ball bearing simulation loads
对3 种角接触球轴承在3 种工况条件下进行仿真,所得仿真寿命如表5 所示。
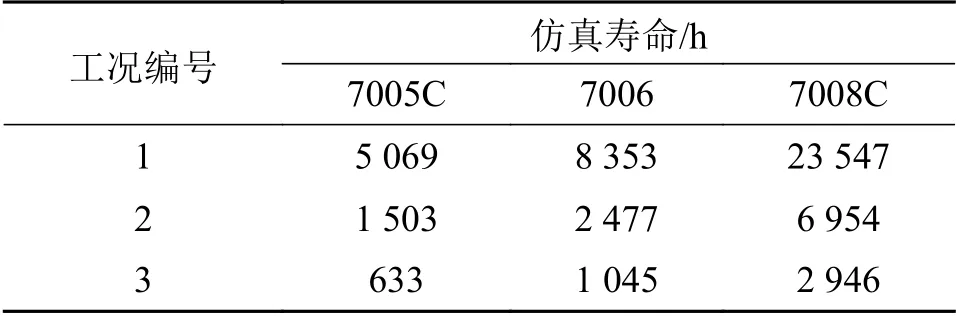
表5 角接触球轴承仿真寿命Tab.5 Angular contact ball bearing simulation life
3.3 轴承可靠性评估
以L10为例进行轴承寿命数据分析,实际工况:轴承转速为12 000 r/min,承受的当量动载荷为1 000~2 000 N 之间的滚动轴承进行可靠性评估,计算轴承的L10寿命。同时利用不同轴承在3 种工况条件下的仿真寿命数据,以平均值的形式表示轴承在该实际工况下的寿命数据。深沟球轴承寿命分析如表6所示,角接触球轴承进行寿命分析如表7 所示。
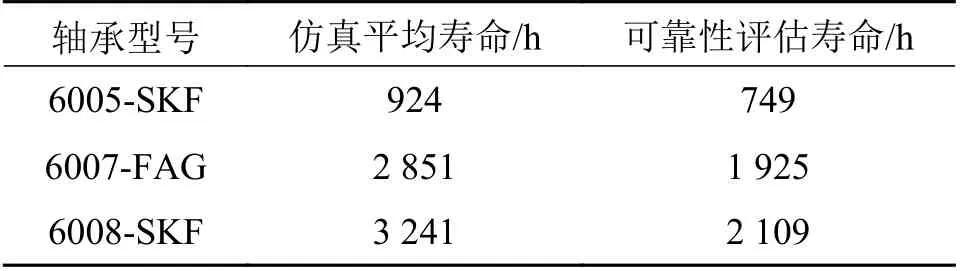
表6 深沟球轴承寿命分析Tab.6 Deep groove ball bearing life analysis
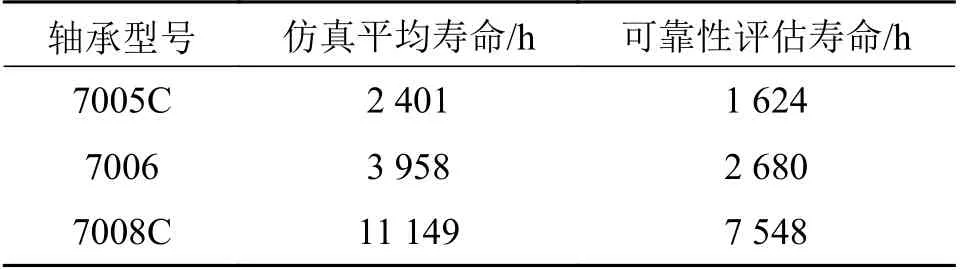
表7 角接触球轴承寿命分析Tab.7 Angular contact ball bearing life analysis
轴承转速为12 000 r/min,承受的当量动载荷为1 000 ~ 2 000 N 下的滚动轴承寿命分析 ,如图3 所示。由图3 可知:仿真平均寿命和可靠性评估寿命具有相似的趋势,说明根据对数正态分布下的轴承可靠性评估与设计模型进行的滚动轴承可靠性评估,所计算出的可靠性评估寿命可以准确反映轴承寿命情况。
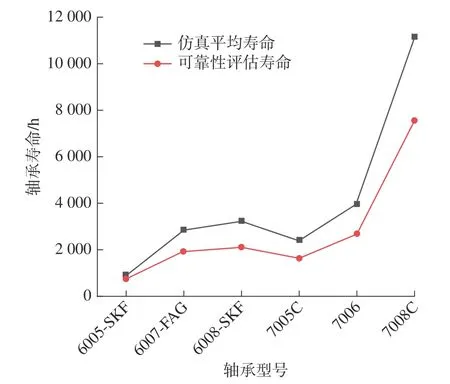
图3 滚动轴承寿命分析Fig.3 Life analysis of rolling bearing
由图3 知:可靠性评估寿命普遍低于仿真平均寿命。因为在考虑施加载荷的波动性的情况下,轴承受交变载荷作用,更易疲劳失效,故而寿命会降低。由此证明可靠性评估寿命更具有安全性,利用计算出的当量动载荷的波动区间(µys,µyf)区间中值进行可靠性评估具有更高的裕度。在滚动轴承应用选取方面可以更加安全有效。
3.4 轴承可靠性设计
以6005-SKF 为例对轴承进行参数优化设计,由寿命数据可知,当实际工况为[1 000~2 000] N-12 000 r/min 时,6005-SKF 的仿真平均寿命为924 h,可靠性评估寿命为749 h。以目标寿命为1 000 h,可靠度为0.9,对6005-SKF 轴承进行可靠性设计。
1)6005-SKF 轴承的额定动载荷Cr=11 200 N,利用式(10)可计算出当量动载荷P0=1 249 N。
2)实际工况下施加的载荷范围[1 000~2 000] N,根据对数正态分布下的轴承可靠性评估与设计模型的式(7)和式(9),计算得到当量动载荷许用范围(1 159,1 764) N。
3)取当量动载荷许用范围的中值P1=1 461.5 N结合目标可靠度寿命L10=1 000 h,代入式(10),计算出可以满足当前工况下目标可靠度寿命的轴承额定动载荷Cr1=13 099 N。
4)以球轴承为例,额定动载荷与轴承参数的设计公式为:
对轴承参数进行优化,要提高Cr可以:减小接触角 α,增大滚动体数Z,增大滚动体球径,改变内外圈沟曲率系数fi,fe,增大系数fc。具体参数优化数值,可对轴承参数进行多决策变量优化得到。
4 结论
本文提出一种应力-强度干涉模型下的滚动轴承可靠性评估与设计方法,可以有效地对轴承进行可靠性评估以及可靠性设计,具体结论如下:
1)考虑滚动轴承的动力学行为,将载荷处理为随机过程,利用对数正态分布模拟载荷分布。基于应力-强度干涉模型将可靠性指标转化为滚动轴承当量动载荷许用范围,考虑滚动轴承的特性可以使得滚动轴承可靠性评估与设计方法更加准确有效。
2)通过对可靠性评估寿命与仿真平均寿命的分析,说明根据应力-强度干涉模型的滚动轴承可靠性评估与设计方法进行的可靠性评估可以准确反映轴承寿命情况,并且具有更高的裕度,可以使滚动轴承应用选取更加安全有效。
3)应力-强度干涉模型下的滚动轴承可靠性评估与设计方法,通过对当量动载荷许用范围的合理取值,结合轴承设计公式,对轴承参数进行优化,使优化后的轴承可以在该工况下满足目标寿命和可靠度的要求,实现滚动轴承的可靠性设计。

