小曲率路面车辆差动转向与横摆稳定性集成控制研究

王重磊 , ，刘珣 , ，黄元毅，张成才 , ，汪怡平 ,

（1.武汉理工大学 汽车工程学院，武汉 430070；2.武汉理工大学 现代汽车零部件技术湖北省重点实验室，武汉 430070；3.上汽通用五菱汽车股份有限公司，广西 柳州 545007）

为减少环境污染、节约能源，电动汽车技术得到快速发展[1]。而分布式驱动电动汽车由于其具有更加灵活的动力分配方式，所以得到更多关注[2-4]。通过控制驱动电机可以有效提高车辆的安全性和稳定性。

目前差动转向控制已有较多学者进行研究，并取得许多有价值的研究成果。如文献[5]针对后轮轮毂驱动车辆的稳定性控制问题,提出了基于分层结构的稳定性控制器，最终实现在整个控制过程中，车轮的滑转率始终保持在最佳滑转率附近，保证车辆获得较大的附着力。耿聪等[6]设计了基于非线性轮胎模型的等效线性观测器，有效的提高了车辆状态观测精度，并在此基础上有效控制车辆处于稳定状态。付翔等[7]结合主动后轮转向技术与四轮转矩分配技术，有效提高了四轮转向车辆瞬态控制性能。Hu 等[8]设计了抗扰动H∞反馈控制器，在很大程度上提高车辆差动助力转向过程中的轨迹跟踪控制能力。王庆年等[9]基于理想差动助力转向模型，以参考方向盘转角与实际方向盘转角偏差作为控制反馈变量，控制前轮毂电机输出横摆力矩，帮助驾驶员进行转向，使得转向更加轻便。Yan 等[10]设计自适应控制器，优化各个轮毂电机之间转矩转速分配，进而提高车辆转向稳定性。文献[11-12]通过实验验证差动助力转向的可行性。但是，以上研究均将差动转向作为辅助转向系统，用以辅助驾驶员完成转向。而实际上，当车辆丧失转向功能时，差动转向系统能够作为唯一的动力源进行转向。而在车辆完全丧失转向能力的情况下，对如何保证车辆轨迹跟踪性能与稳定性的研究较少。

针对无转向能力或转向能力失效的分布式驱动车辆，提出了一种差动转向与横摆稳定性集成控制方法，该方法包括两个控制回路：基于LQR 最有控制算法的差动转向控制回路，用以实现车辆轨迹跟踪控制；基于模糊PID 控制算法的车辆稳定性控制回路。仿真结果验证了所涉及方法的有效性，可以在实现轨迹跟踪的同时提高车辆横向稳定性。

1 差动转向车辆模型

车辆由4 个轮毂电机驱动，为保证车辆在控制时的稳定性以及实时性，需要模型能够同时满足描述准确性要求以及简洁性要求，所以在此基础上做出以下假设：1）车辆在平坦无障碍工况下行驶，忽略车辆由于路面影响产生的垂向运动；2）忽略悬架系统的影响；3）忽略车辆在外力作用下产生的载荷转移；4）忽略车辆纵向以及横向空气动力学；5）前轮转向角度足够小[13]；6）轮胎工作在线性区。基于以上理想假设，构建二自由度自行车模型，如图1 所示。

图1 二自由度车辆动力学模型Fig.1 Two-degree-of-freedom vehicle dynamics model

车辆横摆运动的动力学方程为

式中：Iz为车辆绕z轴的转动惯量； ω˙z为车辆横摆角速度；lf和lr分别为前后轴到车辆质心CG的距离；ΔM1为由左右前轮由于不同纵向轮胎力产生的横摆力矩；Fyf和Fyr分别为前后轮胎横向轮胎力，Fyf =Fyfl+Fyfr，Fyr=Fyrl+Fyrr，Fyi为第i个轮胎的横向轮胎力，其中i=fl,fr,rl,rr。基于前轮转角足够小假设，ΔM1可以表示为

式中：Fxi为第i个轮胎的纵向轮胎力；ls为轮距的一半； δf为前轮转向角。

基于轮胎工作在线性区域假设，则此时横向轮胎力与轮胎侧偏角成线性关系，车辆横摆运动的动力学方程（1）可以改写为

式中：cf和cr分别为前轮和后轮的轮胎侧偏刚度；vx和vy分别为车辆纵向速度和横向速度。

2 转向系统模型

电动线控转向系统结构如图2 所示。当转向系统中转向电机完全失效，此时转向电机不受电子控制单元（Electronic control unit，ECU）控制，由于前轮与方向盘之间结构上并无连接，因此没有外力作用于前轮，最终前轮会停止转向。为了避免因转向系统故障导致的车辆失去转向能力，可由整车控制器（Vehicle control unit，VCU）直接控制左右前轮轮毂电机驱动、制动，从而产生横摆力矩协助驾驶员在转向系统完全失效的情况下完成转向。

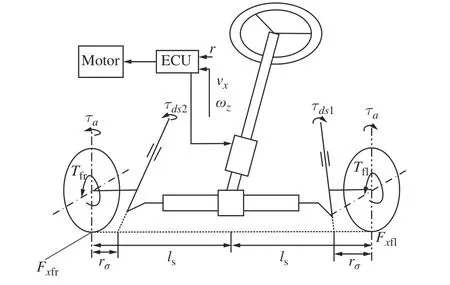
图2 电动汽车转向系统模型Fig.2 Electric vehicle steering system model

如图2 所示，左右前轮的纵向轮胎力Fxfr和Fxfl将分别生成扭矩τds1和τds2，可表示为：

式中rσ为主销接地点与轮胎接地点的正视距离，假设rσ变化足够小，其变化率可以忽略不计。在此假设条件下，当差动转向功能启动时，由左前轮与右前轮之间不同的轮胎力产生的横摆力矩为

车辆在此横摆力矩的影响下产生差动转角，转向系统动态方程为

式中：Jeff为有效惯性力矩；beff为有效转向阻尼；τa为轮胎回正力矩； τf为转向电机、齿轮和齿条摩擦力矩。

本文采用刷子轮胎模型[14]来数学描述轮胎，基于小侧偏角假设， τa可以表示为：

式中： αf为前轮侧偏角；l为轮胎接地印迹长度的一半。

由式（10）可得

整理式（4）～式（11）可得

控制输入量u表示为

整理可得差动转向车辆动力学模型为：

令

整理可得

车辆参考横摆角速度为

式中：kus为车辆稳定性因子； δh为车辆参考前轮转角；lv为车辆前轴与后轴距离。

3 差动转向控制与横摆稳定性集成控制系统研究

基于车辆动力学模型，本文设计了基于差动转向控制器和稳定性控制器的双闭环控制结构如图3 所示。

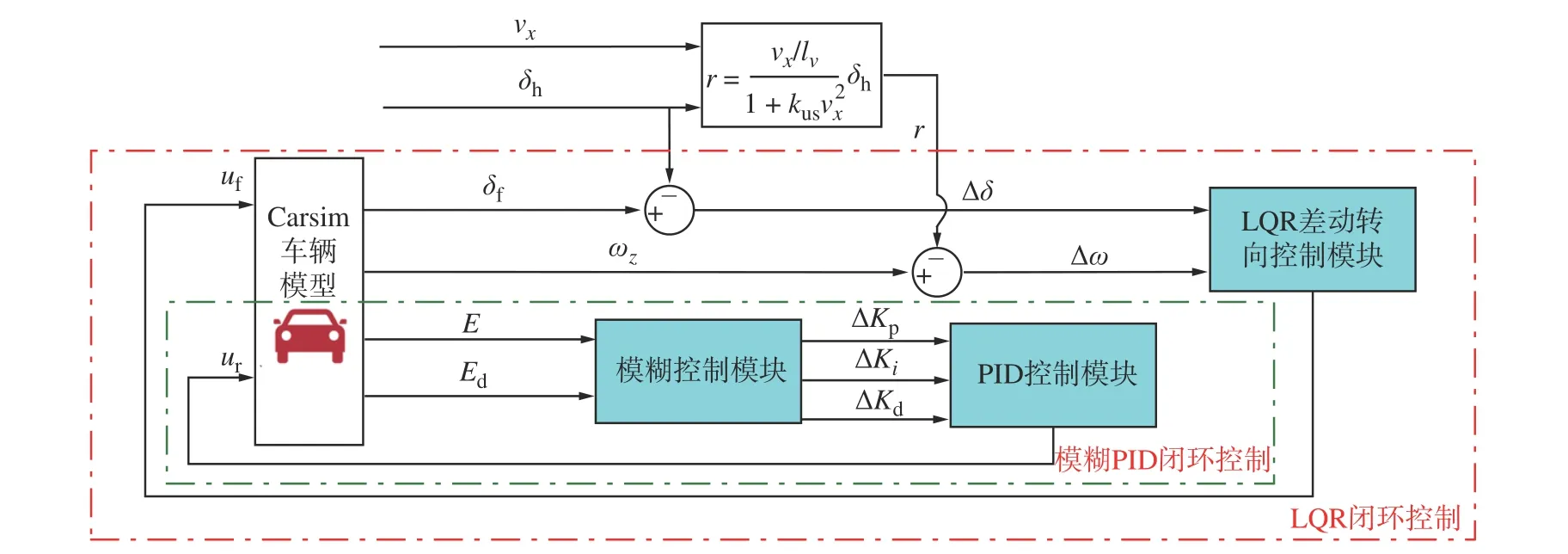
图3 控制系统流程图Fig.3 Control system flowchart

如图3 所示，集成控制系统包括4 部分：基于LQR的差动转向控制器、基于模糊PID 的横向稳定性控制器、车辆模型、二自由度参考模型。系统包括两个控制回路：LQR 车辆控制回路和Fuzzy-PID 控制回路。

LQR 车辆控制回路基于LQR 设计车辆差动转向控制器，控制左右前轮驱动，制动产生横摆力矩，实现车辆在转向系统完全失效时进行转向。控制器以实际前轮转角、实际横摆角速度与参考前轮转角、参考横摆角速度的差为反馈控制变量，产生前轴横摆力矩，实现差动转向的作用。

Fuzzy-PID 控制回路采用模糊PID 控制方法设计车辆横摆稳定性控制器，以提高车辆横摆稳定性。控制器以实际质心侧偏角与参考质心侧偏角的差为反馈控制量，产生后轴横摆力矩，提高车辆横摆稳定性。

3.1 差动转向控制器

在理想假设条件下，车辆系统特性矩阵依然是A和B，此时无直接横摆力矩作用下的系统模型为

式（15）减去式（18）可得

令

式（19）可改写为更一般的形式，即

为了求解车辆直接横摆力矩与系统状态偏差之间的关系，定义如式（21）差动转向系统代价函数，求解在无限时间条件下的直接横摆力矩最优解[15]。

式中：Q和R均为对称正定矩阵，Q∈R2×2，R∈R1×1。

根据最优控制理论可得

式中K为系数矩阵。

式中P为代数黎卡提方程的解。

对于LQR 的差动转向控制器而言，其性能的优劣在于权重系数矩阵Q与R。鉴于差动转向系统的功能需求，取R=1，矩阵Q可表示为

代价函数的表达式为

式中：Q1为差动转向控制系统对横摆角速度偏差的权重；Q2为差动转向控制系统对前轮转角偏差的权重。在车速以及参考前轮转角已知的条件下即可确定系统特性矩阵，通过求解代数黎卡提方程就可以得到最优控制量uf。

令

则

3.2 横摆稳定性控制器

为了实现车辆差动转向过程中横向稳定性控制，定义系统的质心侧偏角偏差为

式中 βr为参考质心侧偏角，βr=0。

输入与输出表达式为

式中：ur(t)为模糊PID 控制器的输出；Kp，Ki，Kd分别为模糊PID 控制器中的比例参数、积分参数、微分参数。ΔKp，ΔKi，ΔKd分别为输入量经模糊规则推导后的比例参数、积分参数、微分参数的增量。模糊PID 控制器输入输出参数如表1 所示。

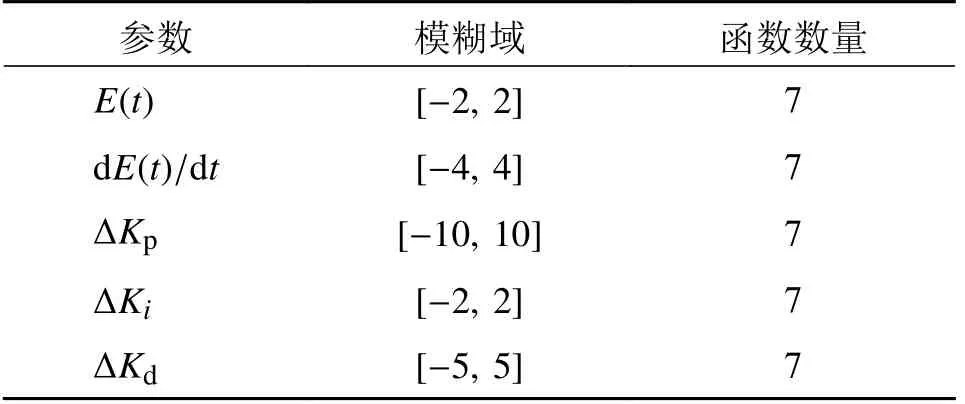
表1 模糊PID 控制器输入输出参数Tab.1 Fuzzy PID controller input and output parameters

确定输入输出变量模糊域后，需要对其进行模糊化处理。通过隶属度函数将精确输入量转化为模糊输出量。一般情况下，一个模糊控制器的模糊语言库可以定义为负大，负中，负小，零，正小，正中，正大；分别以NB,NM,NS,ZO,PS,PM,PB表示。输入量为高斯型隶属度函数，输出量为三角型隶属度函数，隶属度函数曲线如图4 和图5 所示。

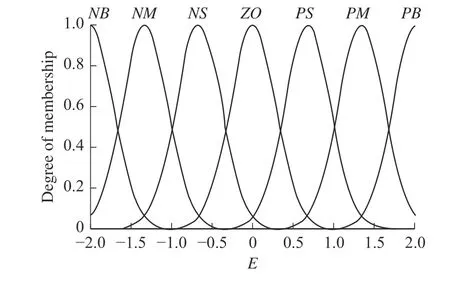
图4 高斯型隶属度函数Fig.4 Gaussian affiliation function

图5 三角型隶属度函数Fig.5 Triangular affiliation function

定义各个变量的隶属度函数后，需要确定模糊控制规则，模糊控制规则是一种基于专家经验的推理规则，而模糊PID 控制器各参数由以下规则确定：

1）当系统偏差E(t)较大时，为保证系统较好的跟踪控制性能，此时Kp应当设定较大值，Kd应当设定较小值，以保证系统能较快响应系统误差。

2）当系统偏差E(t)较小时，为了避免系统达到稳定后出现的震荡，此时Kp，Ki应当设定较大值，Kd应当设定较小值。

3）当系统偏差E(t)介于两者之间时，为了避免系统出现超调现象，此时Kp应当设定较小值，Kp，Ki应当设定合适值。

基于以上参数设定规则建立模糊控制推理机制。令E=E(t)，Ed=dE(t)/dt，模糊推理机制如表2～表4 所示[16]。

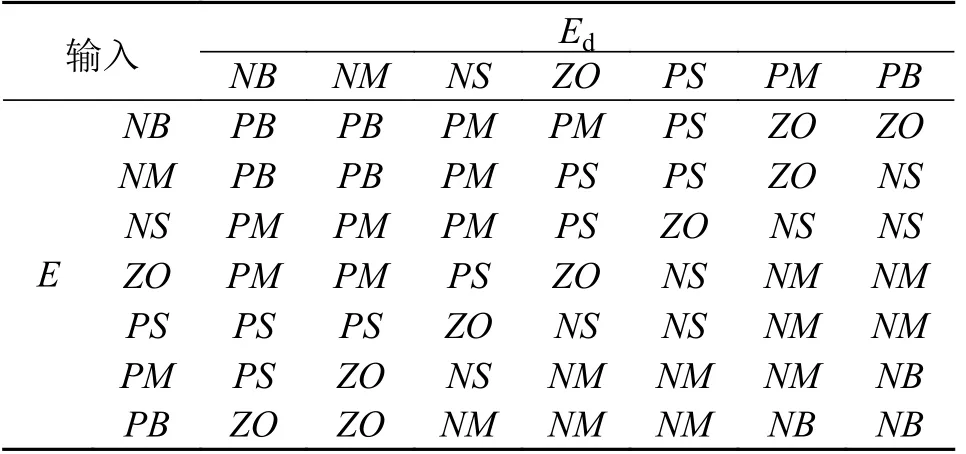
表2 ΔKp 模糊控制规则Tab.2 ΔKp Fuzzy control rules

表3 ΔKi 模糊控制规则Tab.3 ΔKi Fuzzy control rules

表4 ΔKd 模糊控制规则Tab.4 ΔKd Fuzzy control rules

4 仿真分析

为验证本文提出的差动转向控制以及横向稳定性控制方法，本文采用Simulink-Carsim 联合仿真的方法对控制算法进行验证分析。仿真过程中模型参数如表5 所示。仿真输入如图6 所示，车辆在高附路面上（u=0.85）以初始速度10 m/s 行驶，前轮转角以正弦变化，在此输入条件下车辆进行连续转向。转向系统在2 s 时刻失效，仿真结果如图7 所示，无差动转向系统车辆沿失效时刻速度方向偏离参考轨迹，失去控制。在差动转向控制器作用下，车辆具备较好轨迹跟踪能力且轨迹跟踪误差较小。

表5 仿真采用的整车参数Tab.5 Vehicle parameters used for simulation

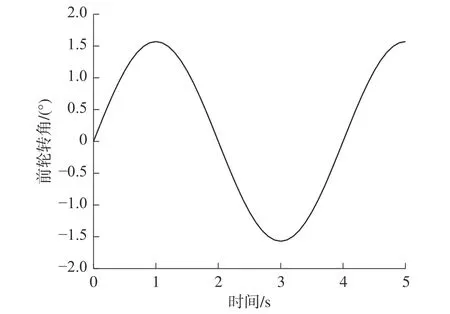
图6 参考前轮转角Fig.6 Reference front wheel turning angle

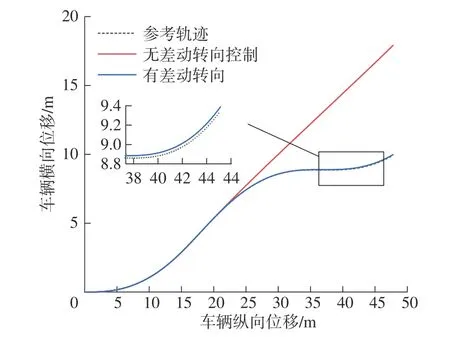
图7 车辆行驶轨迹（2 s）Fig.7 Vehicle movement trajectory (2 s)

如图8 所示，转向系统在0 s 时刻失效，两种控制方法在连续转向工况下都具备良好的路径跟踪能力，差动转向系统的最大路径跟踪误差为0.42 m，跟踪误差呈上升趋势；带有横向稳定性控制系统的车辆路径跟踪能力较好，最大路径跟踪误差为0.21 m。仅由差动转向系统控制的车辆在面对连续转向工况时，路径跟踪能力逐渐下降。这是由于在横向稳定性控制系统的作用下，车辆在连续转向工况，能够较快响应随时间变化较快的前轮转角，以保证其路径跟踪性能。

图8 车辆行驶轨迹（0 s）Fig.8 Vehicle movement trajectory (0 s)

图9 为在连续转向过程中，质心侧偏角随时间的变化情况。其结果说明，在连续转向过程中，横向稳定性控制系统能够有效地抑制逐渐变大的质心侧偏角，抑制车辆在连续转向过程中失稳趋势。这是因为模糊PID 控制器能够快速响应较大的误差变化率，调节控制参数，使得控制器对偏差微分量更灵敏，从而降低跟踪误差。

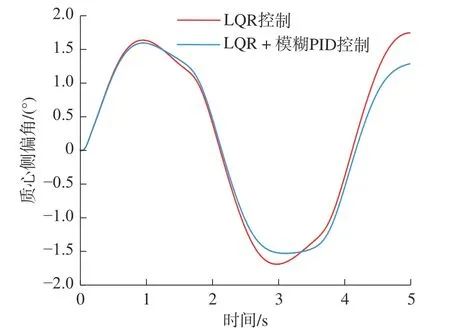
图9 车辆质心侧偏角Fig.9 Vehicle center-of-mass lateral deflection angle

图10 为车辆差动转向过程中前轮电机驱动转矩输出情况，转矩输出仿真结果同车辆前轮转角输入变化趋势相同，由于本文采用左右电机平均分配转矩方式，因此前轴左右电机驱动转矩方向相反，大小相同，与实际情况相符。

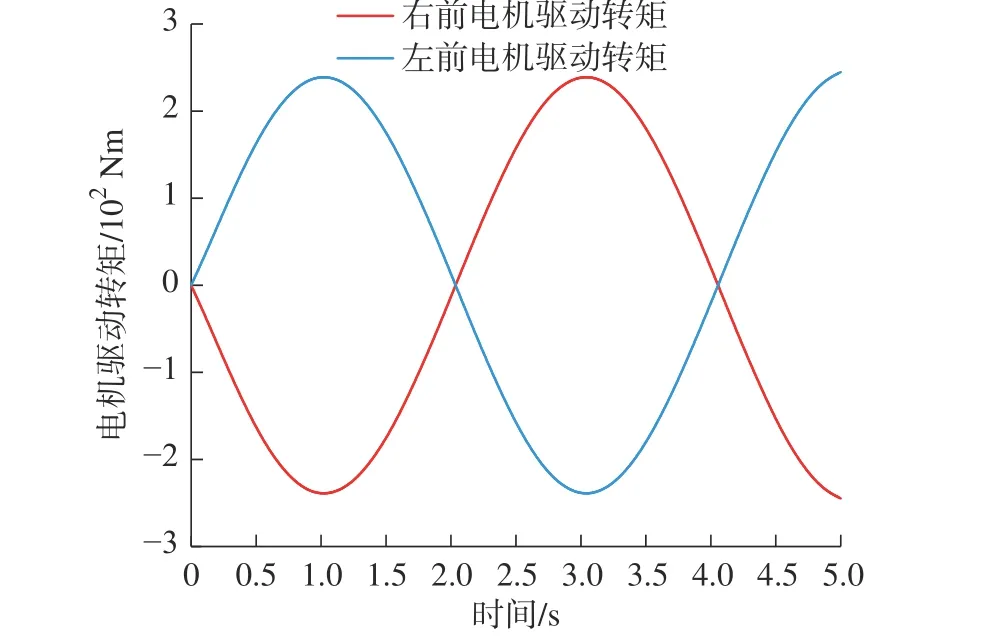
图10 电机驱动转矩Fig.10 Motor drive torque

该仿真结果说明了差动转向系统与横向稳定性控制系统在连续转向工况下的有效性。仅差动转向系统控制使得车辆累计误差逐渐变大，导致其轨迹跟踪能力逐渐下降。横向稳定性控制系统能有效抑制车辆在连续转向过程中的失稳趋势，进而提高轨迹跟踪能力以及横向稳定性。

5 结论

本文针对分布式驱动车辆，设计了基于LQR 最优控制原理的差动转向控制器以及基于模糊PID 的横向稳定性控制器。该控制器能够根据模糊控制规则动态调整PID 控制器控制参数，在差动转向过程中提升车辆稳定性。基于Carsim-Simulink 搭建仿真模型与场景进行仿真实验，仿真结果表明，在连续转向工况下，基于LQR 最优控制原理的差动转向控制器轨迹跟踪性能较差，轨迹跟踪误差逐渐上升；而双闭环结构控制器的适应性较好，能够有效降低连续转向过程中车辆的偏航趋势，进一步提高车辆轨迹跟踪能力、转向稳定性。