飞行器机翼变形驱动机构研究

郭广宇，陈青山，高宏

（北京信息科技大学 仪器科学与光电工程学院, 北京 100192）

飞行器在军事领域中有着举足轻重的作用。为了在复杂多变的战场中灵活地穿梭，飞行器需要根据实时飞行环境调整自身飞行状态，传统机翼已经难以满足需求[1]。而变形机翼综合应用了新材料和运动驱动机构，可以通过内部驱动机构柔顺、平滑地自主改变整体或局部外形，以此适应复杂多变的外部环境，保持优秀高效的飞行性能[2-3]。在众多变形机翼方案中，变弯度机翼通过改变机翼前后缘弯度提高飞行器升力，可以显著改善飞行器气动特性、提升飞行效率，因而成为了变形机翼领域研究的热点[4-7]。

1985—1988 年期间，美国任务自适应机翼项目，通过光滑连续的变弯度后缘提升了飞机的巡航和机动性能[8]。但受限于当时的材料技术水平，变弯度机翼重量过大，实用性不强。2003 年，Elzey 等利用记忆金属设计了一款记忆合金材料控制的铰链变弯度机翼[9]，由于形状记忆合金的变形受温度的影响，且变形速度慢，其工作频率和控制精度难以满足现实环境需求，可靠性有待提高。2010 年，杨媛等设计了分段式变后缘变弯度机翼结构，后缘最大变形12°[10]。2016 年，Previtali 等研究了一款可代替副翼的“增强褶皱蒙皮”机翼，在通电后，后缘的褶皱蒙皮可进行伸缩变形并推动尾部弯度变化，但弯度变化范围较小，升力改进有限[11]。

因此，变弯度机翼技术尚未在飞行器上得到真正的推广使用。本文研究了一种机翼后缘变形方案，采用多级连杆串联驱动结构实现机翼的大角度变形。连杆机构相比于柔性结构有更高的结构强度和系统可靠性，可以实现大角度变形。该方案可以实现机翼后缘±25°的偏转，满足大型飞行器对升力的需求。采用有限元分析验证这种机翼的结构完整性，采用运动学分析和样机实验验证了变形方案的角度变化范围。

1 变弯度机翼构成及原理

变弯度机翼主要通过驱动机构带动蒙皮弯曲偏转实现机翼外形的变化，基本结构如图1 所示。机翼前缘或后缘的箱体内配置有驱动机构，通过改变驱动机构的形态或相对位置可使机翼前缘或后缘变形[12]。机翼外表面覆有柔性材料构成的蒙皮，可随驱动机构的形态拉伸弯曲，以此实现形态的改变。

图1 变弯度机翼构成Fig.1 Composition of variable camber wing

蒙皮影响机翼的变形能力。优质的蒙皮在保证自己法向刚度的同时也要兼具纵向的韧性，可以随机翼的外形发生光滑的大角度变形。在飞行器工作过程中，蒙皮需要强大的承载能力以承受气动载荷，通过调整蒙皮的材料和结构可以有效地提升蒙皮刚度。常用的变形机翼蒙皮材料包括硅橡胶材料、聚合碳纤维材料、聚合环氧树脂材料等，蒙皮结构包括波纹结构、蜂窝结构等[13-17]。聚合碳纤维材料具有更高的拉伸强度但是价格更加昂贵。蜂窝结构具有零泊松比的特点，但是加工工艺复杂。根据机翼性能指标，合理地选择蒙皮掺杂材料和结构铺层可以得到性价比更高的蒙皮。变形机翼蒙皮常见材料与结构性能参数如表1 所示。

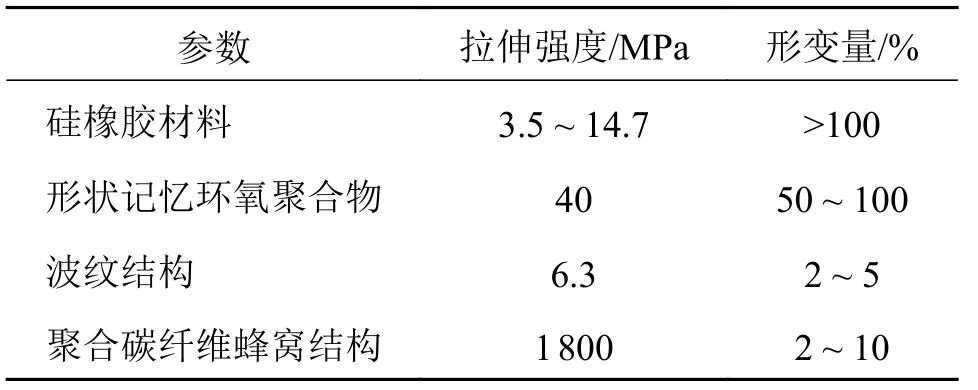
表1 变形机翼蒙皮常见材料与结构性能参数Tab.1 Common materials and structural performance parameters of deformed wing skin

驱动机构负责控制变弯度机翼的变形范围，可以是气囊加压驱动结构、柔性肋结构、鱼骨式弯曲结构、记忆合金结构、连杆驱动结构等[18-20]，对变弯度机翼的性能有最为直接的影响。例如，柔性肋结构产生的变形最为光滑连续，但机翼可弯曲角度范围偏小，多用于驱动机翼前缘变形；记忆合金材料和气囊加压结构的驱动速度相对较慢；鱼骨式结构与连杆结构可以完成大角度变形，但机翼变形曲线光滑度相对较差。选择变弯度机翼的驱动机构需要综合考虑飞行器的尺寸大小及飞行环境等因素。

变弯度机翼通过变化自身翼型控制机翼上下表面气流动压以获得升力。当机翼发生弯曲变形时，其获得的升力也随之增大，飞行器的飞行性能也将得到显著提升。通常用升力系数（CL）表达升力，气流动压和机翼面积之间的关系CL可表示为

式中： ρ为气体密度；V为气体流速；l为机翼表面尺寸特征；L为升力，其表达式为

式中Г为环量，其表达式为

将速度V沿坐标轴分解为3 个方向的分量u、v和w，则升力系数表达式可化简为

变弯度机翼应用于中大型飞行器，旨在为飞行器起降或应对特殊工况时提供必要的升力支持。为提高飞行性能，变弯度机翼CL≥1.2。为达到这一指标，机翼弯曲角度应不小于25°。同时，制定变形机翼方案时需考虑机翼的极限载荷，并保证驱动机构在极限载荷条件下不产生影响飞行安全的有害变形，变形机翼的参数指标如表2 所示。

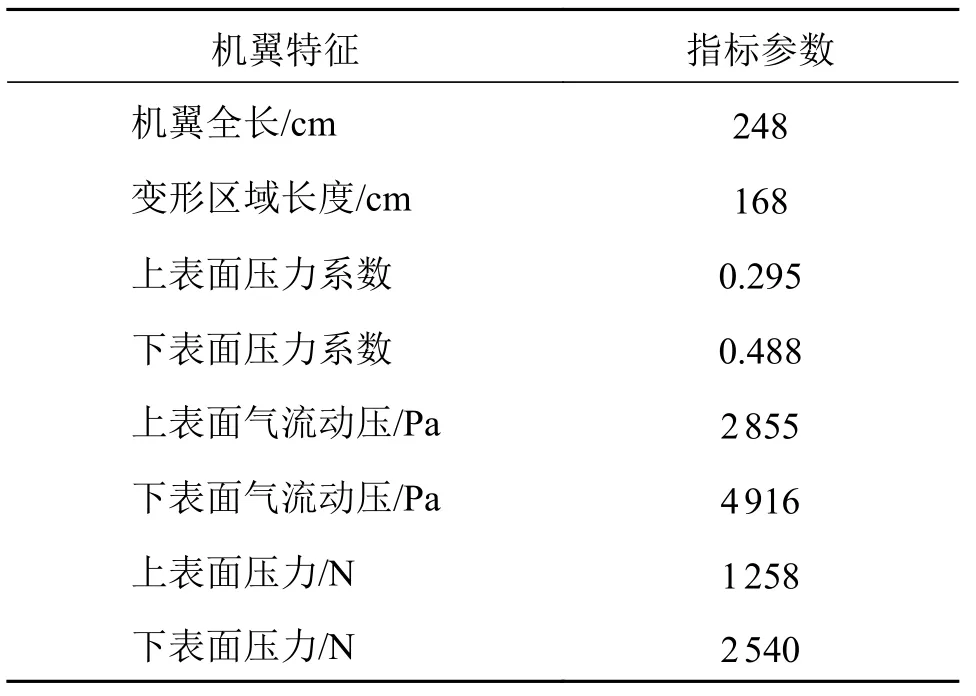
表2 机翼极限载荷条件及几何参数Tab.2 Limit load conditions and geometric parameters of wing

考虑飞行器整体尺寸和载荷，为满足最大CL的需要，结合表1 数据，可选择蜂窝结构的聚合碳纤维材料作为机翼的蒙皮。这种材料在纵向有良好的形变量，满足飞行器蒙皮对延展性的需求。同时，该材料强度优秀，保证蒙皮在极限载荷下不会发生塑性形变。为使机翼后缘角度满足弯曲范围，同时保证驱动机构整体强度，研究了基于多级连杆串联驱动机构控制机翼实现变形。

2 变弯度机翼驱动结构

为使机翼可在±25°范围内光滑、连续地弯曲变形，沿垂直于翼梁方向将部分机翼中段不变形区域和后缘变形区域分为两个单元，如图2 所示，这两单元的内部驱动机构拥有相同的运动原理。通过两组电机分别控制第一和第二单元弯曲变形，可实现机翼后缘的光滑弯曲变形。

图2 机翼驱动机构Fig.2 Driving mechanisms of wing

第一驱动单元内部结构的布置主要考虑曲柄与连杆之间的几何尺寸关系对机翼运动学性能的影响。通过控制各个连杆机构的长度和相对位置关系，获得满足方案要求的输出角度。

第二驱动单元内部结构的布置主要考虑机翼后缘内部可供使用空间大小，根据翼展方向最小截面尺寸对驱动结构进行优化。为了保证机翼运动的同步性，第二驱动单元各个部件的长度比例与第一驱动单元相应部件相同。

机翼的弯度变化通过机构综合的方式实现，驱动机构中各个连杆的关系如图3 所示。通过步进电机控制曲柄转动，带动连杆和摇杆依次传动，将运动和力传递给输出摇杆，实现输出摇杆绕基座输出轴运动。

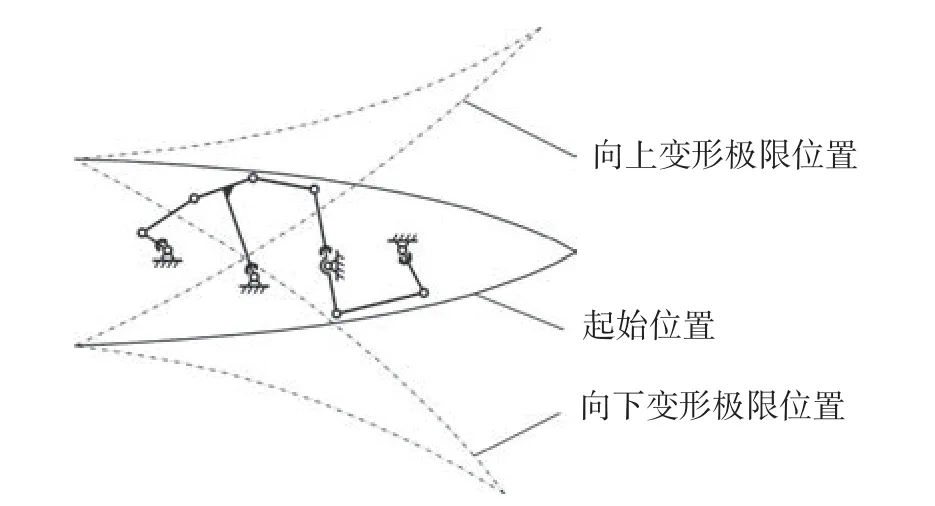
图3 驱动机构原理Fig.3 Principle of driving mechanisms

第一单元中作为机构骨架的机架部分与不变形的机翼中段相连，第二单元的机架与第一单元的输出摇杆相连。曲柄、丁字摇杆、叉形摇杆和输出摇杆约束在机架中的相应位置，通过一字左连杆，一字右连杆和双向连杆相互连接，如图4 所示。曲柄与连杆机构通过销轴彼此连接并固定在机架的指定位置上。这种设计可以有效减少系统运动时轴向受力，并提高致动器力矩沿机构运动方向的传递效率。

图4 驱动机构Fig.4 Driving mechanisms

驱动机构的布置需要考虑机翼本身的几何尺寸和空间结构，尽可能地利用机翼内部有限的空间。根据已知的机翼参数，合理利用机翼中段及后缘空间，研究的机翼驱动机构排布方式如图5 所示。

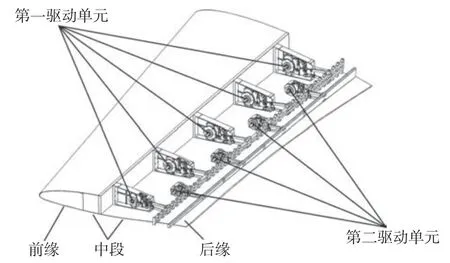
图5 驱动机构整体布局Fig.5 Overall layout of a driving mechanism

3 变弯度机翼完整性分析

变弯度机翼需要适应各种复杂的工况，在飞行过程中展示出良好的气动性能和稳定性。为了验证方案中机翼的完整性，分别对机翼的空气动力学性能、静力学性能和运动学性能进行精确可靠的仿真分析。

3.1 流体力学分析

用Ansys Work Bench 的Fluent 模块对变弯度机翼的空气动力学性能进行仿真分析。设空气为流速0.25 Ma，密度1.225 kg/m3的不可压缩气体，大气压强1.013 25×105Pa，气体黏稠度1.789 4×10-5kg/（m·s），用基于RNGκ-ε模型的压力求解器对机翼进行求解，计算过程忽略热传递。

对变弯度机翼极限弯曲角度情况进行压力仿真分析，图6 为压力场分布。当机翼后缘向下弯曲达到25°时，机翼受到最大压力来自机翼后缘弯曲部分，达到1.078×103Pa，小于下表面最大压强4.916×103Pa。当机翼向下弯曲变形时，机翼上表面气流流速大于下表面流速，由伯努利原理可知，气流在机翼上下表面形成压力差，为机翼飞行提供升力。机翼在仿真环境中获得升力系数CL=1.4。

图6 变弯度机翼压力场分布Fig.6 Pressure field distribution of variable camber wing

仿真结果表明，变弯度机翼所获得的升力可以满足中大型飞行器在起降过程中的飞行需求，并在湍流等特殊环境中为飞行器安全平稳飞行提供升力支持。

3.2 静力学分析

变弯度机翼的驱动核心在于多级连杆串联机构。对驱动机构进行有限元分析，以验证极限载荷条件下各连杆的形变情况。用Ansys Work Bench中的静力学模块对机构进行有限元分析。在软件中生成驱动机构的3D 模型，用六面体单元和四面体单元对模型进行网格划分。采用非线性求解器SOL 400 Nastran 进行求解，其可以在计算大角度旋转时及时更新刚度矩阵。各连杆机构之间的连接关系定义为转动约束，机构7 与机架之间为固定约束，在曲柄机构1 施加200 Nm 的扭矩，并在机构7施加反向的位移以模拟极限载荷下驱动机构的受力情况。

极限载荷条件下驱动机构的应力分布如图7 所示。驱动机构所受应力最大值约为37.3 MPa，出现在叉形摇杆5 与机架的连接部分，小于该结构的屈服强度55.2 MPa。所有其他铝制部件所受应力均小于AL6061 铝合金的屈服强度。仿真结果证明了在极限载荷条件下，各个机构均未发生塑性形变。驱动机构可以支持极限载荷下变弯度机翼的安全飞行。

图7 驱动机构应力分布Fig.7 Stress distribution of a driving mechanism

3.3 运动学分析

驱动机构需要在曲柄旋转一周内实现机翼后缘±25°变形。用Creo Parametric 软件的机构分析功能对驱动机构的运动情况进行分析。各个机构之间，机构与机架之间的装配关系定义为销连接，在输入轴添加一个电动机，为曲柄提供10 rad/s 的输入角速度。用电机控制曲柄转动60 s（曲柄旋转一周），每2 s 采集一次数据，共采集30 组，仿真分析得到数据结果如图8 所示。在机翼曲柄绕输入轴旋转一周内，机翼驱动机构绕输出轴转动60.33°，其中向上极限弯曲角度为30.16°，向下极限弯曲角度为30.17°，输出曲线光滑连续，表明可以弯曲变形角度范围优于所需±25°。

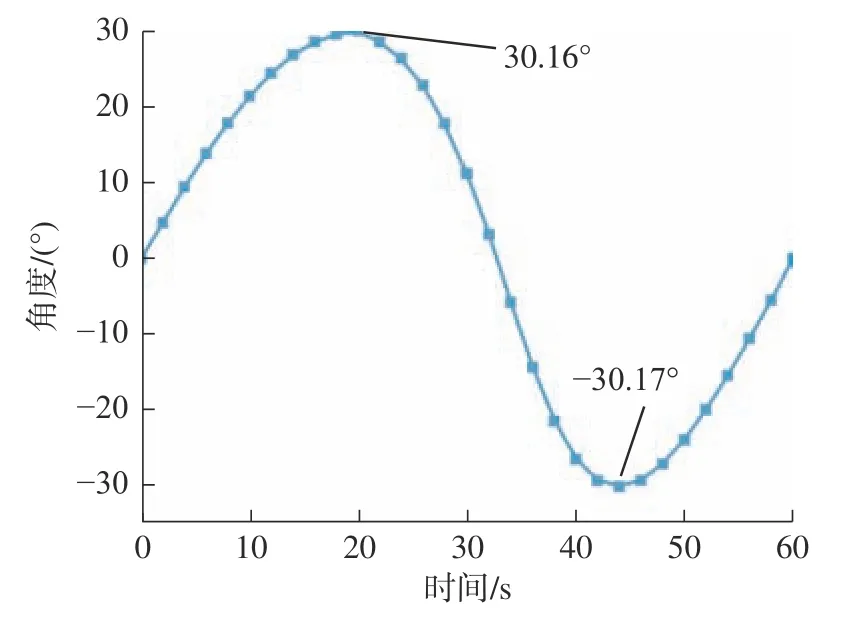
图8 输出轴转动角度Fig.8 Rotation angle of output shaft

4 变弯度机翼性能试验

依据方案设计并组装了试验用变弯度机翼样机，对方案中的机翼进行了运动学性能试验，实验样机如图9 所示。

图9 实验样机模型Fig.9 Experimental prototype model

上位机设定电机转速值并发送控制指令给ARM 处理器。经过功率驱动后，步进电机根据该指令驱动机构运动，实现机翼后缘弯曲变形，系统如图10 所示。

图10 变弯度机翼控制系统示意Fig.10 Schematic diagram of variable camber wing control system

样机可以实现60 s 内从初始位置到达最大外倾角位置的连续弯曲变形。如图11 所示，通过角度传感器采集机翼变形角度数据表明，机翼向下最大偏摆角为30.12°，向上最大偏摆角为30.06°。试验数据与仿真结果吻合良好，证明了变弯度机翼方案在实现机翼大角度变形的可行性。

图11 变弯度机翼偏转角度Fig.11 Deformation angle of variable camber wing

5 结论

研究用于飞行器连续变弯度机翼的多级连杆驱动机构，实现了机翼上下极限位置之间的弯度连续变化，可用于复杂的飞行环境。驱动机构具有可靠的结构强度，确保了飞行器工作安全。相比于传统固定翼机翼，变弯度机翼可以提供更大的升力。变弯度机翼系统可控性良好，在大型飞行器机翼设计制造领域有广阔的应用前景。