CEEMD-VMD 与参数优化SVM 结合的托辊轴承故障诊断
贺志军 , , ,李军霞 , , ,刘少伟 , , ,秦志祥 , ,
(1.太原理工大学 机械与运载工程学院,太原 030024;2.山西省矿山流体控制工程技术研究中心,太原 030024;3.矿山流体控制国家地方联合工程实验室,太原 030024)
托辊作为带式输送机的重要组成部分之一,其运行状态对输送机的安全运转有着重要意义。由于托辊故障造成的事故比比皆是[1-2],究其故障发生的原因主要表现在内部轴承上,例如托辊轴承失效时温度可急剧上升到700 ℃以上[3]。而轴承在发生早期故障时,故障信息中含有大量噪声导致特征提取困难。因此,对托辊轴承信号降噪是故障诊断的关键。
针对这一难题,学者们提出了许多解决方法。Huang 等[4]提出了经验模态分解(Empirical mode decomposition, EMD)的信号分解方法,EMD 将数据分解为数个本征模态分量,再从中提取故障特性,但该方法有着模态混叠和端点效应等问题,严重影响它的使用。在此基础上,集合经验模态分解(Ensemble empirical mode decomposition, EEMD)通过添加白噪声的方式解决了EMD 模态混叠的问题[5],但添加的白噪声对后续的处理有一定的干扰。随后,Yeh 等[6]提出了互补集合经验模态分解(Complementary ensemble empirical mode decomposition,CEEMD),他通过添加可以抵消的白噪声进行了优化。曹玲玲等[7]利用CEEMD 对轴承故障信号进行降噪后进行包络解调分析,结果表示可以有效地得到故障特征频率。但是在强噪声的背景下,从前期故障信息中提取微弱特征还存在一定的困难。因此,有必要对CEEMD 分解之后的信号进行进一步的降噪处理。Dragomiretskiy 等[8]提出的一种新的时频分析方法-变分模态分解(Variational mode decomposition, VMD),在处理非线性、非平稳信号上效果明显。任朝晖等[9]将VMD 与DBN 相结合对轴承故障信息进行处理取得了不错的效果。该方法一经提出便受到许多学者的关注,但其也存在对噪声敏感的特性。
支持向量机是一种适用于小样本机器学习故障分类方法[10]。杜占涛等[11]将小波变化和支持向量机相结合用于轴承故障诊断,结果表示可以有效识别故障位置。但其性能的优劣依赖于惩罚因子c和和参数g的选择。周建民等[12]采用遗传算法(Geneticalgorithm,GA)来优化参数,李怡等[13]采用麻雀算法(Sparrow search algorithm, SSA)来优化参数,但优化效果都存在着一定的不足。樽海鞘群算法[14]作为一种新的寻优算法,有着寻优能力强的优势。本文通过樽海鞘群算法优化支持向量机参数,用来提升SVM 的分类精度。
鉴于此,本文提出一种基于CEEMD-VMD 双重降噪的托辊轴承故障诊断方法。解决了单一降噪方法的弊端,采用寻优能力更强的优化算法来提升支持向量机的分类精度。通过测试数据集来验证该方法在实际生产中的应用,最后通过对比验证所提方法的可靠性和优越性。
1 基本原理
1.1 互补集合经验模态分解(CEEMD)
CEEMD 将可以相互抵消的白噪声加入原信号,利用白噪声频率均匀分布的统计特性,经过EMD 分解进而达到抑制模态混叠的目的。因本文篇幅有限,CEEMD 算法分解原理见参考文献[6]。
分解后模态分量的筛选是初步降噪的关键。合适的模态分量可以提高信号的信噪比。本文综合峭度和相关系数原则来进行选择IMF,之后将其进行重构,用来排除无关信号的干扰。
峭度因子K的定义为
式中: µ为故障信号x(t)的均值; σ为故障信号x(t)的标准差;E为数学期望。
相关系数R的定义为
式中:f和 µk分别为原始信号和分解后的模态分量;和分别为其均值。
轴承在发生故障时会伴随着冲击信号,相应的峭度也会增大,因此可以用峭度来表示轴承故障,但是峭度易受瞬时冲击的影响,为此引入相关系数来克服这一弊端。将峭度大于3 且相关系数大于0.1 的IMF 筛选出来进行信号重组,这些模态分量中包含着大量的故障信息,这样可以完成信号的初步降噪。
1.2 变分模态分解(VMD)
区别于传统方法,VMD 是一种完全非递归的信号处理方法。通过提前确定分解模态的个数,在分解过程中自适应地匹配每种模态的最佳中心频率和有限带宽的方法,从而达到对模态分量(IMF)的有效分离。VMD 方法具体如下:
1)构建变分问题,其约束条件为分解的各分量之和为原信号,约束表达式为
式中:K为需要提前确定的分解模态个数;{µk},{ωk}分别为分解之后第K个模态分量和中心频率;δ(t)为狄拉克函数; *为卷积运算符;f(t)为原信号。
2)求解变分问题,通过引入二次惩罚因子 α和Lagrange 乘法算子 λ的方法,将约束变分问题转变为非约束变分问题,得到增广Lagrange 表达式为
对式(4)采用交替乘子算法对其求最优解,运算如下:
式中 ψ为收敛精度,一般取1×10-7。
从VMD 分解得到的模态分量选取最优IMF 是降噪的最后一步,笔者选用包络熵和包络谱峭度相结合的复合指标(Composite impact index, CII)对IMF 进行选择。
唐贵基等指出如果IMF 包含故障特征较多时,当信号呈现的稀疏性越强,包络熵越小,反之包络熵值越大。因此可以用包络熵作为指标对IMF 进行筛选,包络熵Ep计算方法见参考文献[15]。但包络熵存在着一定的缺陷,为了弥补包络熵在表征冲击信号上的不足,引入对冲击信号敏感的峭度指标。峭度值越大代表冲击信号越丰富,包含的的故障信息越多,反之则越少。包络谱峭度Kv计算方法见参考文献[16]。结合包络熵和包络谱峭度指标,本文提出了复合指标C,计算公式如下:
1.3 樽海鞘群优化支持向量机(SSO-SVM)
樽海鞘优化算法作为较新的优化算法,在每次更新中,追随者在领导者的指导下,不断向食物逼近。领导者负责全局探索,追随者扮演局部探索的角色。因此具有较强的寻优能力。算法具体流程见参考文献[17]。
支持向量机性能的优劣主要取决于惩罚因子c和核函数参数g的选取,因此利用樽海鞘群算法较强的寻优能力来实现参数的自适应选取。樽海鞘群优化支持向量机的流程如图1 所示。
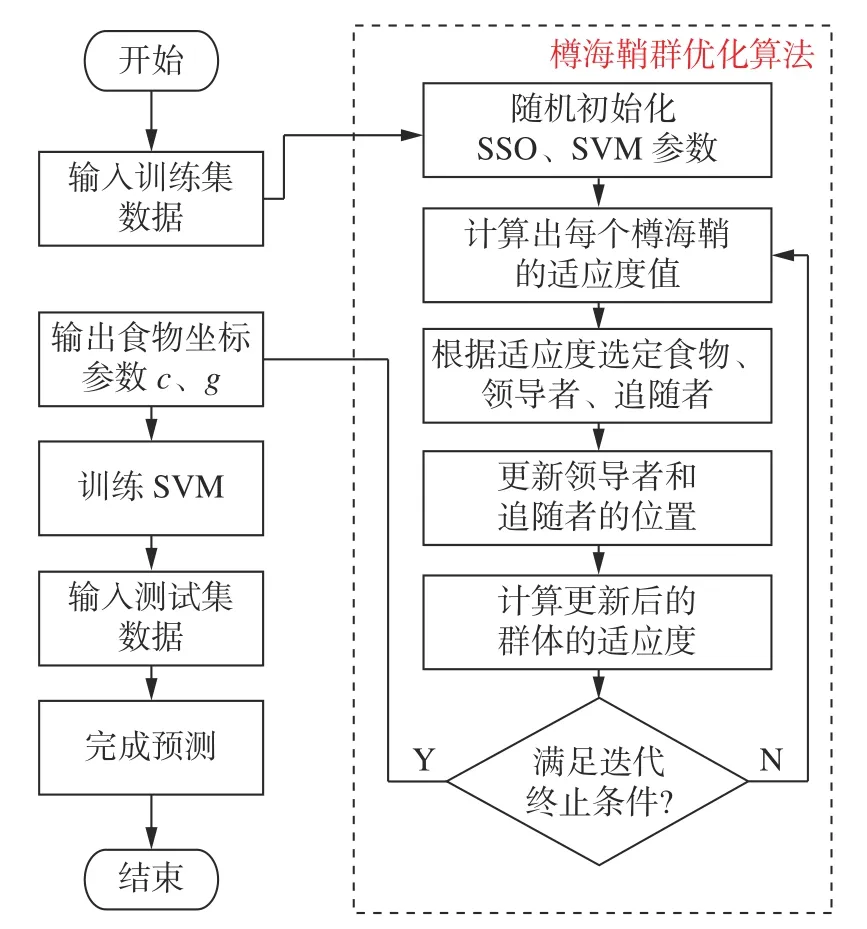
图1 SSO-SVM 流程Fig.1 SSO-SVM flow chart
具体步骤如下:
步骤1 将训练数据输入SVM。
步骤2 初始化SSO 参数,因为是两个参数的优化,所以空间上界设为[100,100],空间下界设为[0.01,0.01],种群规模设为20,迭代次数50。
步骤3 计算樽海鞘个体的适应度并进行排序,前一半视为领导者,后一半视为追随者。
步骤4 更新领导者与追随者的位置。
步骤5 计算更新后的个体适应度,与现阶段进行比较,择优保留。
步骤6 重复步骤3 ~ 步骤5,迭代更新直到满足终止条件输出食物位置参数,即SVM 所求参数,之后将测试数据输入SVM 验证其分类准确率。
2 诊断流程
基于CEEMD-VMD 双重降噪的托辊轴承故障诊断流程如下:
1)将轴承3 种工况数据分为训练样本和测试样本两类。将其由CEEMD 进行初步分解,通过计算峭度指标和相关系数进行初步筛选模态分量,达到初步降噪的目的。将筛选出的分量进行重构组成新的信号。
2)将重构信号由VMD 再次处理,并挑选出复合指标最大的模态分量作为最终处理完成的信号。
3)提取信号的排列熵、样本熵、包络熵、包络谱峭度和功率谱峭度5 种指标作为特征。
4)将训练样本输入SSO-SVM 模型用于模型的训练,之后把测试样本输入训练好的模型进行故障诊断。
托辊轴承故障诊断流程如图2 所示。
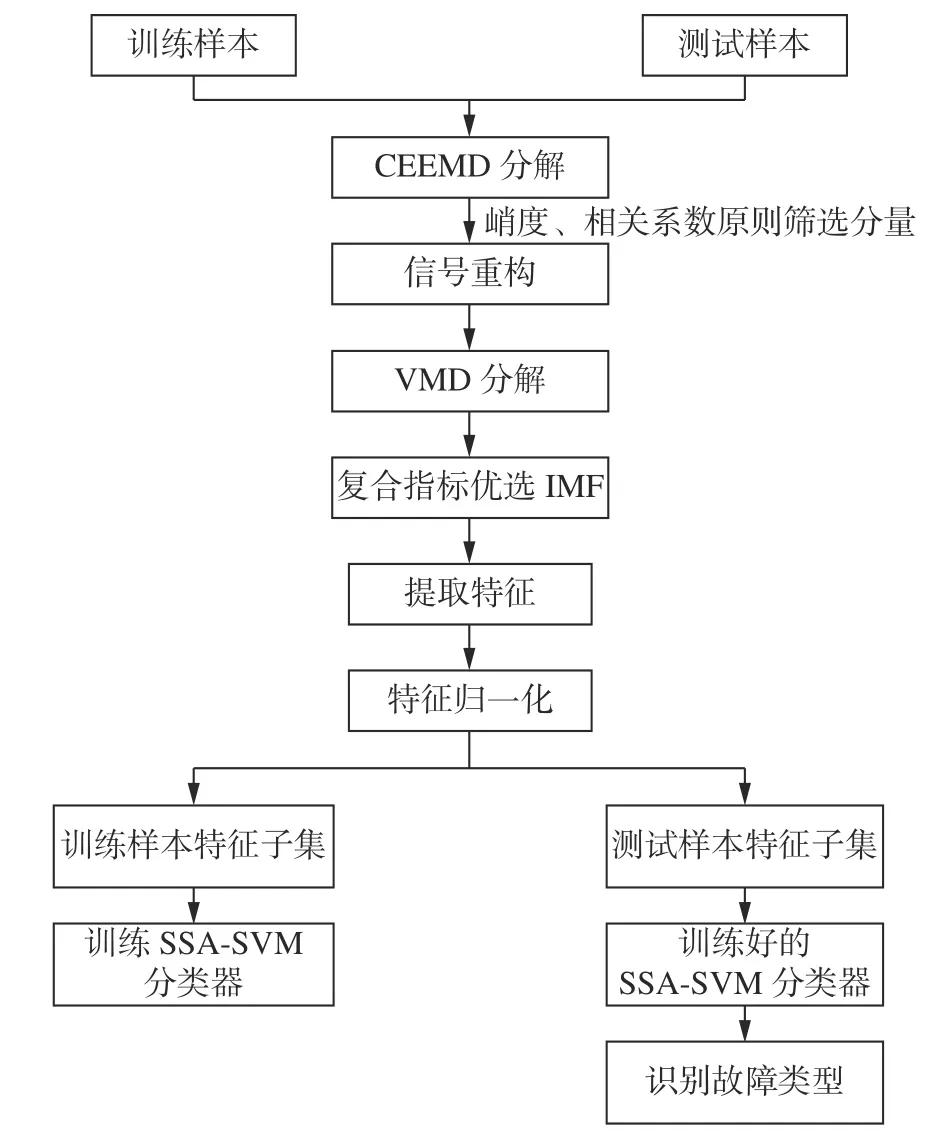
图2 诊断模型图Fig.2 Diagnostic model
3 实验分析
为验证本文所提方法的可行性,笔者使用线切割技术分别在轴承内外圈加工出裂纹,加上正常轴承共3 种工况。对其进行故障诊断分析,如图3所示。

图3 轴承工况图Fig.3 Bearing working conditions
在实验台进行正常托辊轴承、内圈故障、外圈故障3 种工况(标签信息分别定义为0,1,2)实验数据的采集,实验台如图4 所示。实验中,轴承型号为6204 深沟球轴承,其中带式输送机速度设为1 m/s,传感器采样频率为5 120 Hz,根据轴承型号和试验工况,计算可得托辊轴承外圈故障频率为fBPFO=10.9 Hz。数据通过滑动窗口(每个窗口为2 048 个数据点)取样获得3 种工况各50 组数组,共150 组样本数据。训练样本和测试样本按照7∶3 随机分配,其中训练样本共105 组,测试样本45 组。托辊轴承3 种工况时域波形图如图5 所示。

图4 托辊轴承实验台Fig.4 Idler bearing test bench
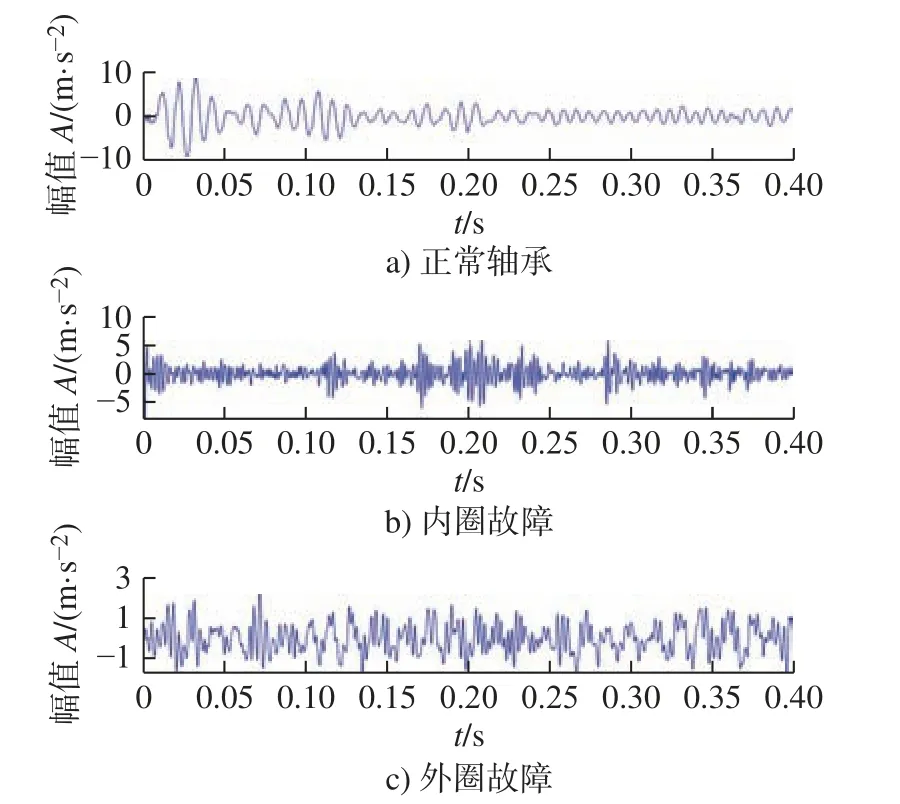
图5 托辊轴承3 种工况时域波形图Fig.5 Time domain waveform of three working conditions of an idler bearing
采用本文所提方法对外圈故障信号进行分解。首先对原信号进行CEEMD 分解,生成15 个IMF和一个余量。分别计算各分量的峭度值以及各分量与原信号之间的相关系数,分别如图6 和图7 所示。

图6 峭度值(经CEEMD 分解的外圈故障信号)Fig.6 Kurtosis values (outer ring fault signal decomposed by CEEMD)
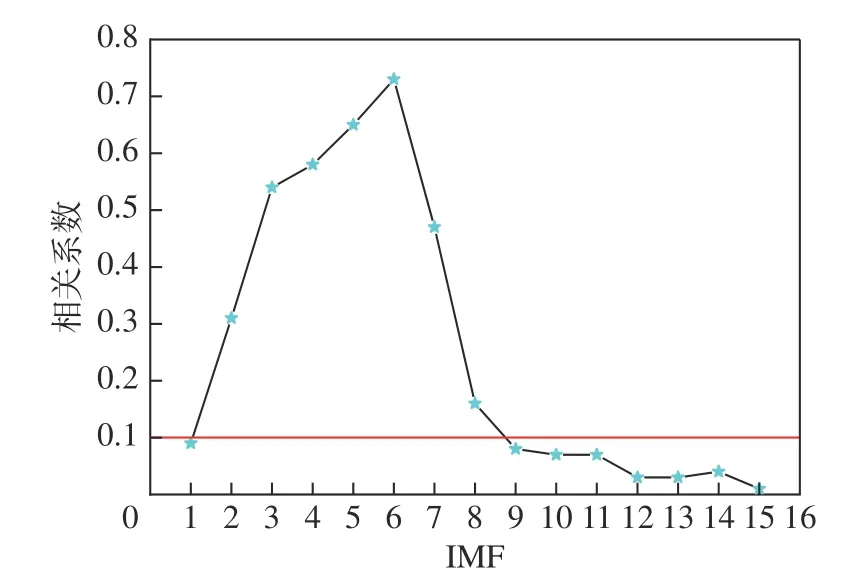
图7 相关系数(经CEEMD 分解的外圈故障信号)Fig.7 Correlation coefficients (outer ring fault signal decomposed by CEEMD)
由图6 和图7 可知:分量IMF2,IMF3,IMF4,IMF5,IMF6,IMF7峭度值大于3 且相关系数大于0.1,故选其进行重构信号,完成初步降噪。
对重构信号进行VMD 分解,在进行VMD 分解时,模态个数K的选取是最为关键的。为避免过分解,本文参考文献[18],通过对比各个模态的中心频率进而对K进行选取,最终将K值设为5,参数α为2 000。图8 为VMD 分解的5 个模态分量图。分别对其求复合指标如图9 所示,IMF3复合指标最大,选其为最终分解的信号进行特征采集。
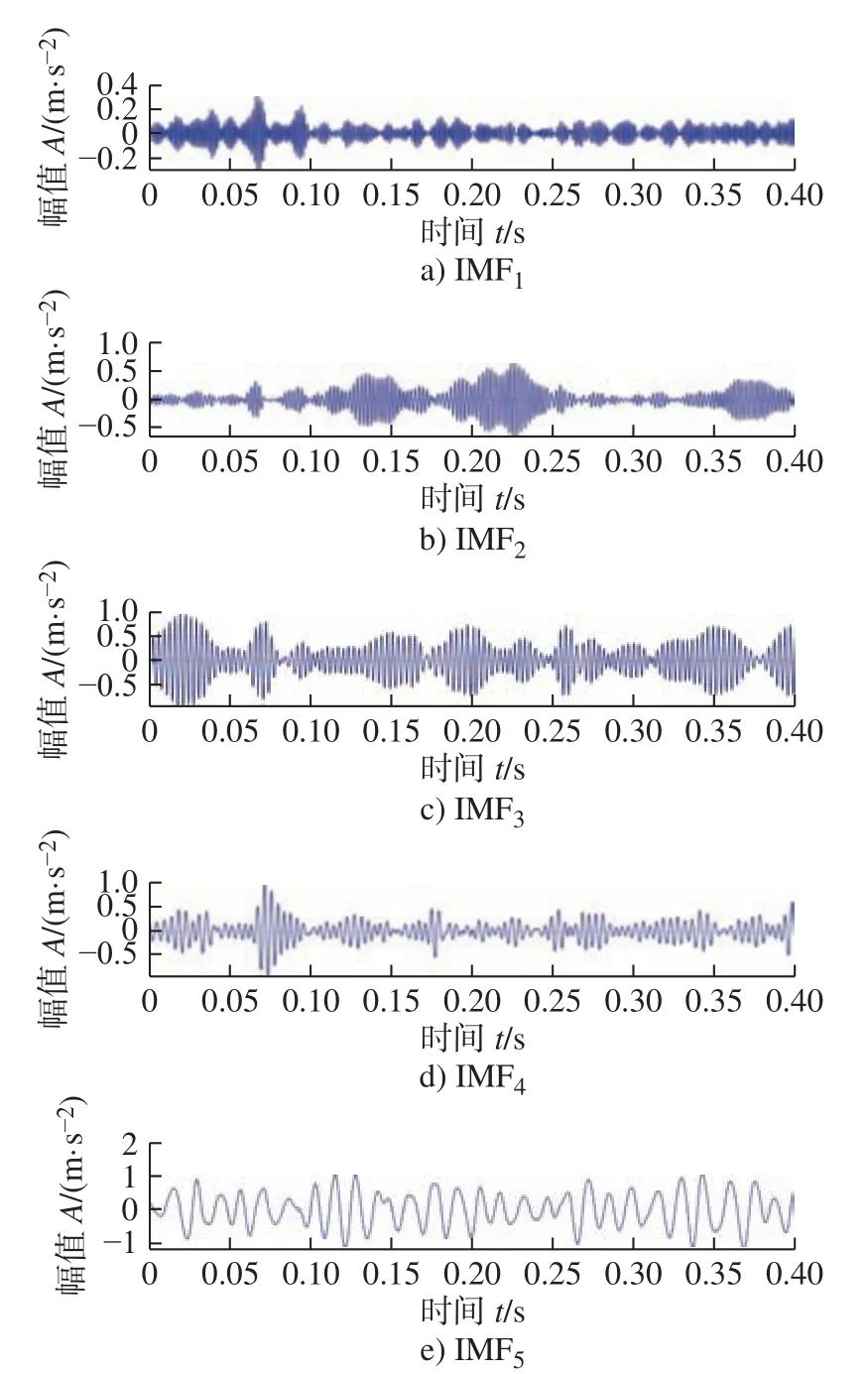
图8 VMD 各模态分量的波形图Fig.8 Waveform of each mode component of VMD

图9 IMF 复合指标评价图Fig.9 IMF composite index evaluation
将最终挑选出的IMF 分别对其求排列熵、样本熵、包络熵、包络谱峭度、功率谱峭度5 种特征组成特征集,之后输入SSO-SVM 模型完成分类识别,分类图如图10 所示。由图10 可知:45 个样本分类中只有一个外圈故障样本误判为内圈故障样本,分类准确率达97.78%,由此验证了所提方法的可行性与准确性。
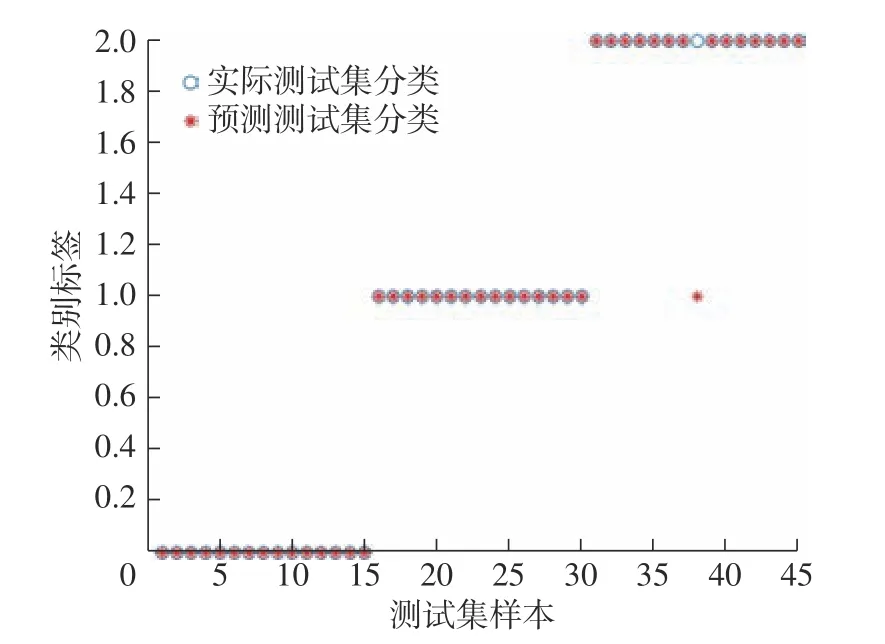
图10 SSO-SVM 分类模型图Fig.10 SSO-SVM classification model
为了验证CEEMD-VMD 方法的降噪效果,分别求取3 种方法降噪之后的信噪比SNR 和均方根误差RMSE 作为评价指标进行对比,结果如表1 所示。
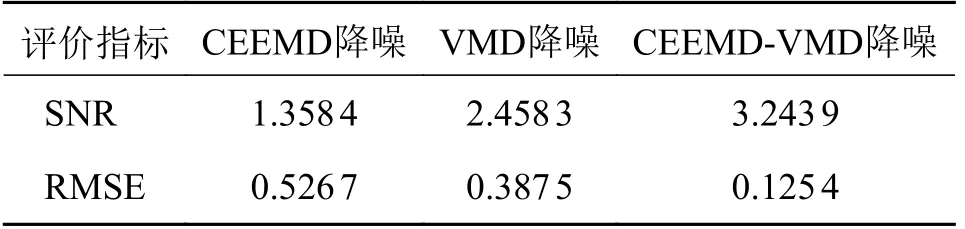
表1 外圈故障3 种降噪方法的评价指标Tab.1 Evaluation indexes of three noise reduction methods for outer ring faults
指标计算公式如下:
式中:x(t)为原信号;x′(t)为处理之后的信号;N为数据长度。
由表1 所示,本文所提方法信噪比更高,而且均方误差更小,相较传统方法有着明显优势,表明使用该方法降噪效果更加显著。
为了能够直观地对比本文所提方法的优越性,分别将外圈故障原始信号用上述所提的3 种降噪方法处理后,对处理之后的信号进行包络解调分析,3 种包络谱如图11 ~ 图13 所示。图11 为CEEMD方法处理的结果,从中可以看出由于受到噪声的干扰,故障特征频率被严重掩盖在故障频率之中。图12为VMD 方法处理的结果,较前者有了明显的改善,但是在故障特征频率周围依旧存在的干扰频率。图13 为本文所提方法处理的结果,从包络谱中可以清晰的看到故障特征频率,与理论计算的结果十分接近,而且从图中还可以找到多个倍频,能够清晰看到托辊轴承外圈故障频率。结果表明,本文所提方法能够有效地对故障信号进行降噪,准确提取到轴承的故障信息。
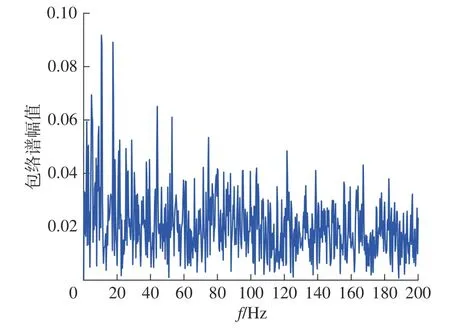
图11 CEEMD 处理信号的包络谱图Fig.11 Envelope spectrum of CEEMD processed signals
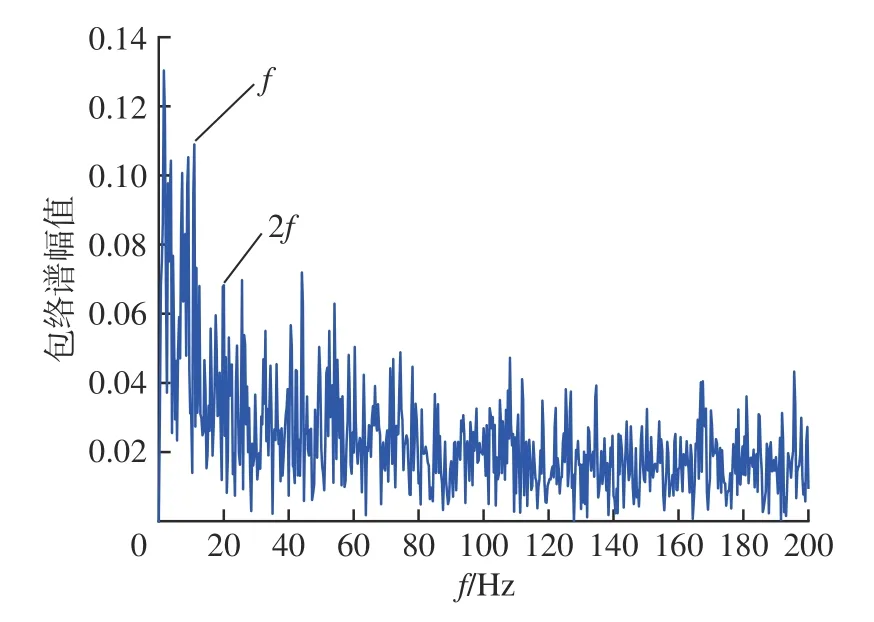
图12 VMD 处理信号的包络谱图Fig.12 Envelope spectrum of VMD processed signals
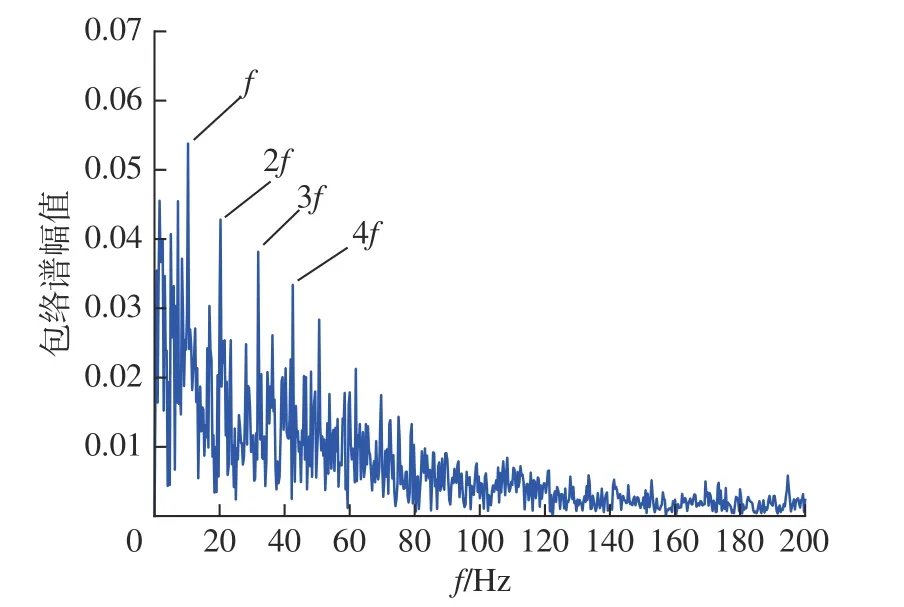
图13 本文方法处理的包络谱图Fig.13 Envelope spectra processed by this method
为了验证SSO 算法在优化SVM 模型上的优越性,分别采用经典遗传算法(GA)优化SVM 参数和麻雀算法(SSA)优化SVM 参数。之后分别将数据输入SSO-SVM 模型、GA-SVM 模型、SSA-SVM 模型进行分类准确率和运行时间的对比。为了防止偶然事件的干扰,分别进行10 次实验,取10 次实验的平均值进行对比,运行效果如表2 所示。从表2 中可以看出,无论是识别准确率还识别用时方面,本文所提方法都明显优于其他模型。
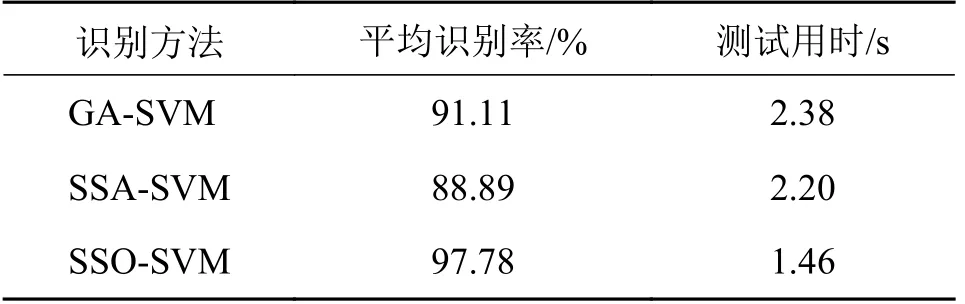
表2 不同分类器结果对比Tab.2 Comparison of results of different classifiers
4 结论
1)针对轴承早起故障信息易被噪声掩盖、难提取等问题,本文提出CEEMD-VMD 双重降噪处理。对比传统降噪方法,此方法降噪效果明显,处理之后的信号无论信噪比还是均方根误差均比传统方法有优势,为轴承故障诊断的降噪方法提供新参考。
2)在SVM 参数惩罚因子c和参数g优化上,本文采用樽海鞘群算法对其进行寻优操作,使得可以自适应确定参数,提升了支持向量机的分类精度,相较其他优化算法,从分类时间及分类准确率的对比中,可以明显看到SSO-SVM 模型有着明显的优势。

