改进粒子群算法的自动充电机械臂时间最优轨迹研究
朱浩,赵清海 , ,郑群锋,宁长久
(1.青岛大学 机电工程学院, 山东 青岛 266071;2.青岛大学 电动汽车智能化动力集成技术国家地方联合工程研究中心,山东 青岛 266071;3.北京理工大学 机械与车辆学院,北京 100081)
随着无人驾驶和5G 技术的大力发展,电动汽车自动充电这一领域成为研究大热,而以关节型机器人作为执行机构的自动充电装置由于小巧、灵活的特性在自动充电领域被广泛应用[1]。诸多研究与应用表明,关节型机器人的运动轨迹规划,不单是能够实现运动任务,还要考虑运动的平稳性、平滑性、电机能耗与工作效率,从而实现多维度的最优轨迹规划。国内外学者针对轨迹规划研究有时间最优、能量最优、冲击最优和综合最优几个方面[2],其中以时间最优研究最多。
时间最优的轨迹优化是指满足动力学或运动学约束条件,机械臂完成相同路径所用时间最短的轨迹[3]。对机械臂的运动轨迹进行时间优化的方法有多种[4],如灰狼算法[5]、遗传算法[6]、粒子群算法[7]、蚁群算法[8]等。田兴华等[9]对惯性权重因子实施双重选择策略,并在局部寻优中加入扰动算子,增强了粒子群算法的突跳能力,较之传统粒子群,寻优能力得到改善。陈波等[10]采用双种群粒子群算法,将种群分为随机群和跟随群,克服时间最优求解过程中易陷入局部寻优的缺点。随着智能算法的改进发展,智能算法凭借其求解优化问题效率高而被广泛应用于机械臂轨迹优化和智能驾驶路径规划中。巫光福等[11]在机器人路径规划中,对全局最优粒子速度更新进行干扰,提高了收敛速度,在避障的同时缩短了运动时间。李东洁等[12]通过引入三次多项式规划运动空间轨迹,最后基于遗传算法进行时间优化求解。邓伟等[13]通过引入五次多项式规划运动轨迹,针对运动轨迹时间最优问题,提出一种基于双种群遗传的混沌优化算法,提高了收敛速度与寻优能力。Jin 等[14]将蚁群算法和粒子群算法等多种智能算法混合,对机器人运动轨迹进行时间最优研究。臧继元等[15]首先采用高阶混合多项式插值进行轨迹拟合,获取插值路径点,然后采用动态学习因子的粒子群算法进行时间最优求解,优化了基本粒子群算法后期局部收敛的不足。
上述研究表明,遗传算法和粒子群算法等智能算法在机器人运动轨迹和智能驾驶路径规划中运用广泛。而传统的遗传算法交叉与变异具有随机性,求解效率相比于粒子群算法较低。粒子群算法求解具有方向性,在大多数情况下,其粒子的收敛速度快于遗传算法,粒子迭代更新后期易陷入局部收敛无法获得最优解。本文采用非线性动态改变学习因子的粒子群优化算法对桁架充电机械臂的运动轨迹最优时间问题进行研究,避免陷入局部寻优的同时进行桁架机械臂运动轨迹的时间优化。
1 改进D-H 法建模
1.1 改进D-H 坐标系建立
桁架充电机械臂的总体结构如图1 所示,是由移动桁架,伸缩机械臂,旋转关节等构成的一种5 自由度充电机械臂。理论上,其可覆盖桁架立方区域,并为充电口布置在车身不同位置的电动汽车进行充电。为了简化正逆运动学求解难度,采用改进D-H坐标系进行建模,基座标系与坐标系1 的原点重合。
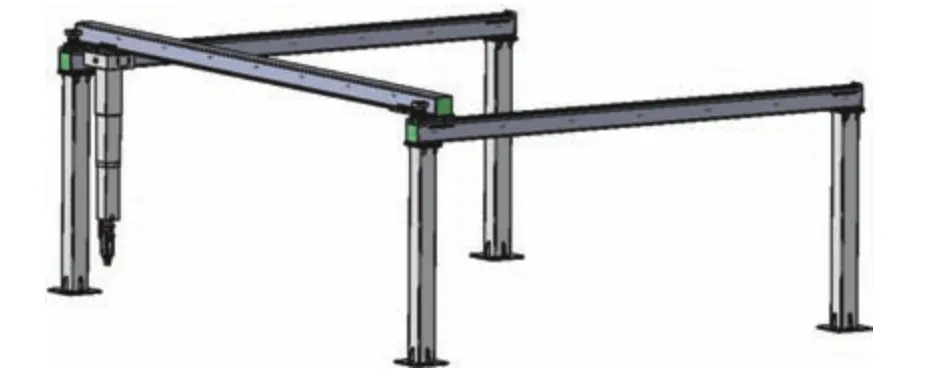
图1 桁架充电机械臂三维模型Fig.1 Three-dimensional model of truss charging arm
依据D-H 坐标系的建立原则,对桁架充电机械臂进行建模,其改进D-H 坐标系如图2 所示。

图2 桁架充电机器人改进D-H 坐标系Fig.2 Improved D-H coordinate system for trusscharging robot
1.2 D-H 参数表
对桁架自动充电机器人进行标准D-H 建模,获取运动学模型的D-H 参数, θ、d、a和 α分别代表关节转角、连杆偏移、连杆长度和连杆扭转角。以此为基础,生成的D-H 参数如表1 所示。

表1 D-H 参数表Tab.1 D-H parameters
1.3 运动学求解
关节角已知,求取桁架充电机器人末端的空间姿态和位置,这个过程就是正运动学求解。相邻两连杆的齐次变换矩阵为
式中:cqi=cosqi;sqi=sinqi。
相邻两连杆的变换矩阵由式(1)可以推导可得:
由相邻两连杆的其次变换矩阵可以推出桁架充电机器人执行端相对于基于的总齐次变换矩阵为
其中,桁架充电机器人末端姿态方程为:
1.4 解析法逆运动学求解
根据目标位置点的空间位置,求解关节1,关节2和关节3 的移动距离。
将式(5)化简可得
由式(6)可知:
解关节4 和关节5 的转动角度分别为:
1.5 工作区域分析
桁架充电机械臂的工作空间是指该装置正常运行时所能到达的空间范围,即末端关节坐标系的原点在空间活动的最大范围[15],如图3 所示。
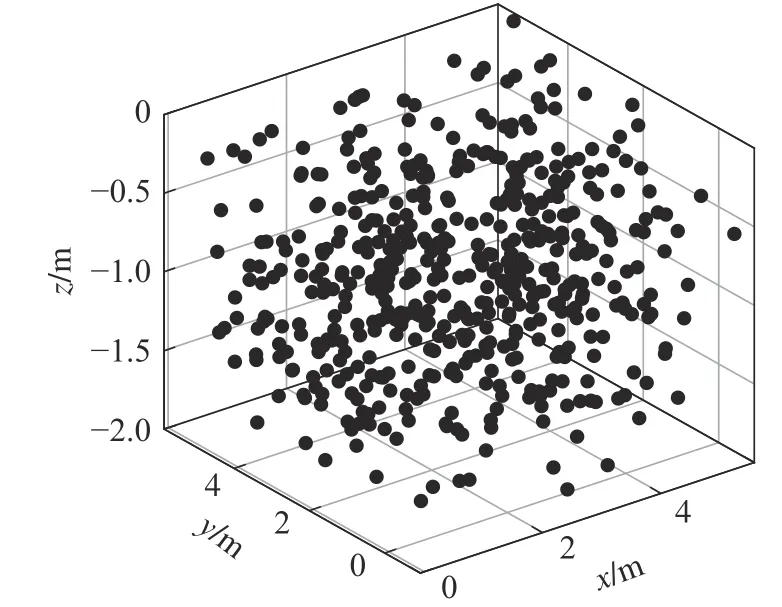
图3 桁架充电机机械臂工作区域分析Fig.3 Analysis of the working area of the truss charging arm
将桁架充电机械臂的工作空间记作W(P)。则关节的运动变化量和工作空间的关系可表示为
式中:W(P)为桁架机械臂的工作区域;Q为空间约束。
从图3 可知,桁架充电机械臂可以覆盖整个立方区域,使得各关节配合能到达工作区域的任意一点,x轴方向,机械臂的工作范围可达(0, 5.5) m;y轴方向,机械臂的工作范围可达(0, 5.5) m;z轴方向,机械臂的工作范围可达(-1.8, 0) m。根据运动工作域,可以更好的配置关节大小,并轨迹规划做准备。
2 充电机械臂轨迹优化
2.1 3-5-3 多项式运动轨迹插值模型
机械臂轨迹规划要考虑运动的平顺性,也就是说既要保证轨迹的平顺性还要考虑位移和加速度不发生突变,因此对运动过程中速度和加速度进行约束,低阶次多项式容易使加速度产生突变,高阶次多项式虽然可以保证加速度的平顺性,但计算量高且导致运动曲线凸包性变差,综上采用3-5-3 多项式插值进行轨迹规划。
当一个充电运动周期的轨迹由3-5-3 多项式插值时,其轨迹运动表达式为:
式中:L1(t),L2(t),L3(t)均为充电机械臂各关节3-5-3多项式插值的运动轨迹。
对3-5-3 多项式插值进行多项式系数求解,可得:
2.2 时间优化目标
针对桁架充电机械臂的运动轨迹时间优化,已知运动起点与终点的速度及其运动过程中的速度约束,适应度函数及其约束条件可表示为:
2.3 改进粒子群算法
基本粒子群算法是模仿鸟类觅食行为,采用速度-位置搜索模型迭代获取最优解的一种智能算法,其表达式为:
式中:w为惯性权重因子;m为粒子迭代次数;i为第i个粒子;c1,c2为学习因子;r1,r2为[0, 1]之间的任意值;xid为粒子的位置,满足空间位置约束;vid为粒子的速度,也满足速度约束条件。
惯性权重系数采用线性递减,Wmax= 0.9,Wmin=0.4,既可以保证有良好的全局搜索能力,又能兼顾其局部搜索能力。
在基本粒子群算法中学习因子一般取0 ~ 4 之间的定值,此处改进粒子群算法中的学习因子采用非线性动态学习因子,可以提高局部收敛的能力。
式中:n为当前粒子迭代次数;N为粒子最大迭代次数。
基于改进粒子群算法求解桁架充电机械臂最优时间优化流程如图4 所示。

图4 改进粒子群轨迹时间优化流程图Fig.4 Improved particle swarm trajectory time optimization flow chart
3 时间优化实验仿真分析
搭建的桁架充电机械臂时间优化实验平台如图5 所示,该平台由桁架充电机械臂、控制箱体、电动汽车、PC 端等构成。以该实验平台为基础进行运动轨迹时间优化实验。

图5 桁架充电机械臂时间优化实验平台Fig.5 Experimental platform for time optimization of truss charging robot arm
参照图5 搭建的实验平台构建桁架充电机器人运动仿真虚拟工作平台,将桁架充电机械臂简化为3 个移动自由度,2 个旋转自由度的串联机器人运动模型,如图6 所示。通过对比在真实与虚拟实验情况下改进粒子群与基本粒子群运动时间优化数据,来验证所提算法的有效性。

图6 桁架充电机械臂运动学三维模型Fig.6 Three dimensional kinematic model of truss charging robotic arm
以桁架充电机械臂为研究对象,根据正逆运动学求解获知运动的起始点和终止点的空间位置,并获取该位置点下关节的移动和旋转变化量。再调用机器人工具箱里的库函数得到该运动轨迹中的两个插值点,最后对4 个路径点所构成的3 段区间进行3-5-3 多项式插值规划,并基于改进和基本粒子群进行时间优化分析,如表2 所示。

表2 各关节空间运动变量插值点Tab.2 Interpolation points of motion variables in each joint space
图7 为关节1 ~ 关节5 位置迭代过程中3 段插值曲线进入收敛时的时间分布情况,随着粒子的更新迭代,3 段插值轨迹收敛所用迭代次数减少。在第一段插值曲线中可知关节1、关节3、关节4 和关节5 很快进入收敛,所用时间分别缩减至3.160 s、2.095 s、2.350 s 和2.000 s,关节2 由于速度处于临界速度,随迭代次数增加,时间不会进行优化,仍处于4 s。若对关节2 运动时间进行优化,需调高关节电机速度,更改速度约束。在第二段和第三段插值曲线中关节2 的情况类似。上述结果表明在3 段插值曲线中各关节所用的收敛时间都得到了优化与改善。

图7 关节1 ~ 5 最优粒子位置迭代各曲线时间分布Fig.7 Time distribution of the optimal particle position iteration curves for joints 1-5
图8 为关节1 ~ 关节5 在改进粒子群算法和基本粒子群算两种情况下的收敛过程对比,从图中可知,改进后的粒子群算法关节1 ~ 关节3 的总体收敛速度比基本粒子群算法的收敛速度要快,由于关节4 与关节5 为转动关节,是充电过程中的后置动作,比较容易陷入局部收敛,因此要达到收敛,所需要粒子的迭代更新次数更多,因此基本粒子群算法在关节4与关节5 收敛所用的迭代次数大于关节1 ~ 关节3,而采用非线性动态学习因子的粒子群算法在关节4与关节5 处的收敛速度也明显快于基本粒子群,提高了后期收敛的速度,进一步优化了运动时间。
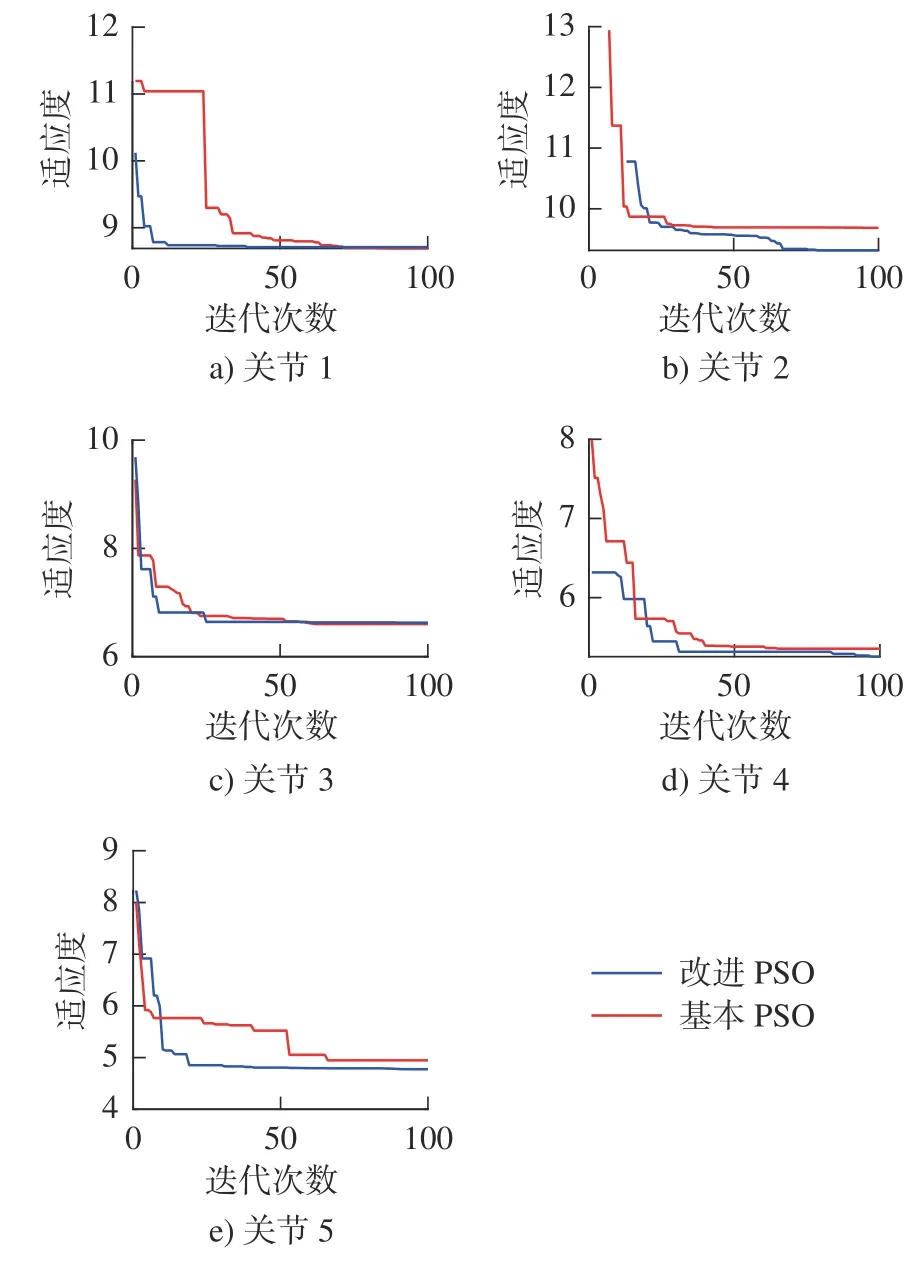
图8 关节1 ~ 5 的两种算法收敛过程对比图Fig.8 Comparison of convergence processes between two algorithms for joints 1-5
图9 为改进粒子群与基本粒子群算法的位置、速度和加速度对比图,结果表明:充电机械臂由起始点经过插值路径点到达终止点,充电机械臂规划的轨迹运动平滑,速度过渡平顺,运动时间有效减少。优化前,位置曲线呈现先上升后下降的趋势,说明关节1 ~ 5 运动过程中出现超出插值点又返回的现象,所以优化前的速度曲线的变化范围为-0.2 ~ 0.6 m/s,这也造成充电机械臂运动时间过长。优化后,关节1 ~ 5位置曲线呈现逐步上升的趋势,速度曲线由静止状态先增加0.7 m/s,然后在此速度附近波动运行一段时间后,最后下降至0,整体运动速度曲线呈现梯形样式。运动时间由运动距离最长的关节2 决定,运动时间由优化前的15 s 缩减到10 s。加速度曲线优化前后对比,优化后加速度曲线变化更为剧烈,但加速度小于1 m/s2,仍满足约束条件,运动时间优化得到预期仿真效果。为了验证仿真结果的真实性,采用图5 的桁架充电机械臂时间优化实验平台进行实验验证,分别测得10 次基于改进粒子群桁架充电机械臂运动时间,对比仿真模拟优化所得运动时间可知,改进粒子群算法优化时间基本与仿真结果相符合,波动范围未超过10%,如图10 所示,进而表明改进粒子群算法对桁架充电机械臂运动时间优化的适用性。
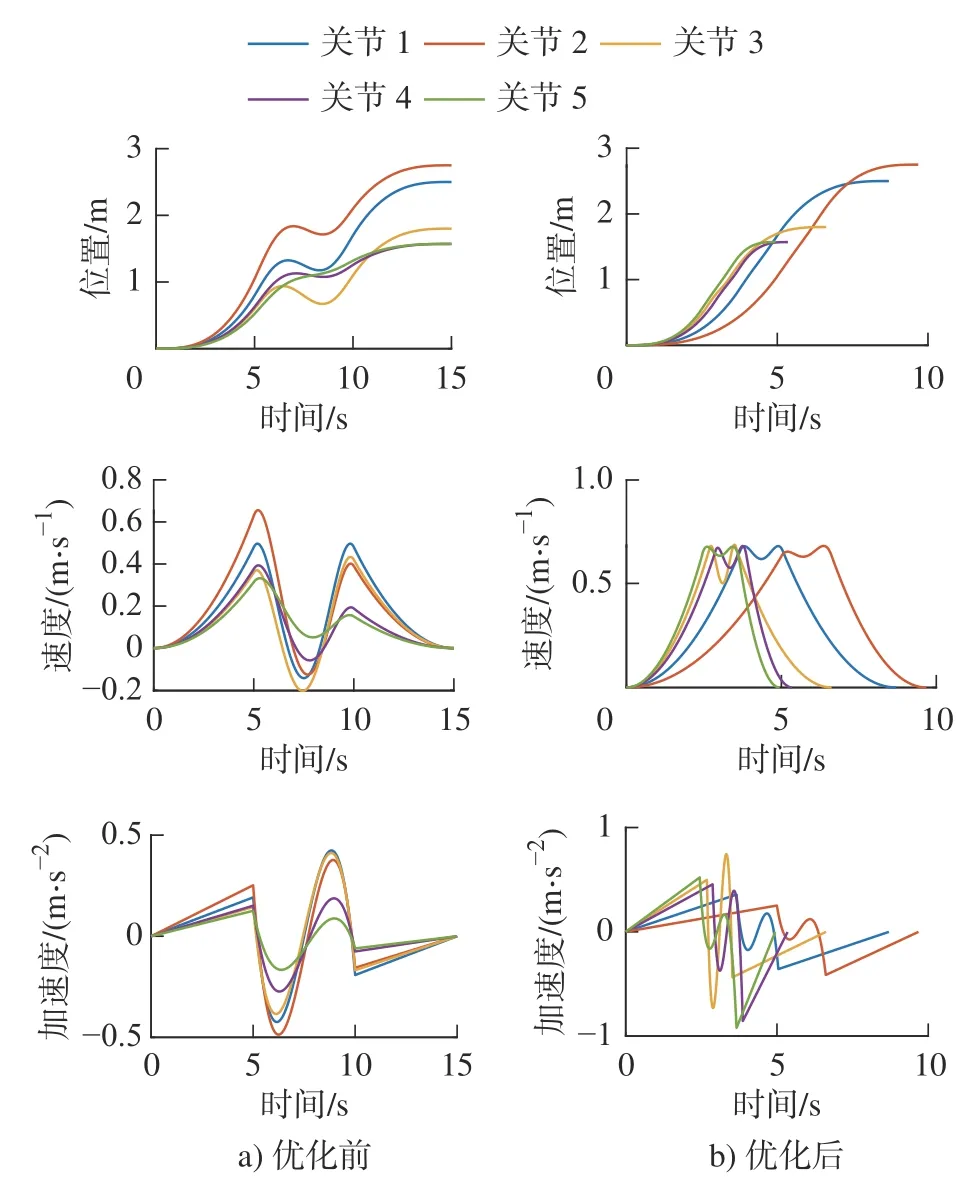
图9 优化前后位置、速度与加速度对比Fig.9 Comparison of position, velocity, and acceleration before and after optimization
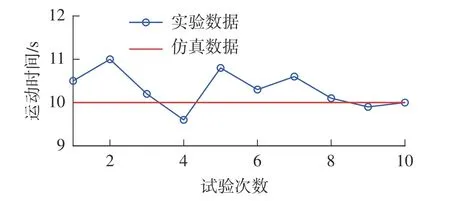
图10 实验与仿真时间优化结果对比图Fig.10 Comparison of experimental and simulation time optimization results
4 结论
仿真结果表明,采用非线性动态学习因子的改进粒子群算法在满足运动学约束条件下,可以寻找到时间最优路径。非线性动态学习因子,克服了基本粒子群算法在时间优化求解过程中易陷入局部收敛的问题,提高了全局搜索寻优的能力,加快了粒子的收敛速度,进而缩短了桁架充电机械臂轨迹运动时间。运动时间由15 s 变为10 s,缩短了33%,最后通过实验对比验证,证明了所提算法的有效性。

