枢轴量为单峰分布的最短区间估计

刘瑞香

数理统计是具有广泛应用的数学分支，而区间估计问题在其中占有很重要的地位。在固定的置信度下，一般认为置信区间的长度越短越好。而用传统方法得到的置信区间一般不是最短的。因此最短区间估计就成为文献中研究较多的问题之一。文[1]研究了正态总体方差的最短区间估计，文[2]研究了伽玛分布参数的最短置信区间。在区间估计问题中，常常构造的枢轴量是单峰分布，如正态分布，t分布，χ2分布，F分布等。文[3]研究了当未知参数的分布为单峰分布时的最短区间估计问题。本文在文[3]基础上用构造枢轴量的方法来讨论枢轴量为单峰分布的最短区间估计，证明了当未知参数分别在枢轴量的分子和分母上时最短置信区间是存在且唯一的；进一步给出了求参数最短区间估计需满足的条件。

定义1[3]设连续型随机变量X的概率密度为 f(x),在(-∞,+∞)(或(0,+∞))内有唯一极大值点 x0，则称X的分布为单峰分布，点x0称为其峰点。

从定义可以看出，若X为单峰分布的随机变量，其概率密度为 f(x)，x∈(-∞,+∞)(或(0,+∞))，x0为其峰点，则当 x＜x0时，f′(x)＞0; 当x＞x0时，

引理[4]若连续型随机变量X为单峰分布，x0为其峰点，其概率密度为 f(x)，x∈(-∞,+∞)(或(0,+∞))，且当x→±∞(或x→0+,+∞)时，f(x)→0，则对任意 b＞x0，必存在唯一的a＜x0,使 f(a)=f(b).

下面只讨论 f(x)定义在(0,+∞)内情况，在(-∞,+∞)内情况同样可以讨论。

设X1,X2,…,Xn是来自总体X的样本，总体X的分布函数为 F(x,θ)，其中

θ＞0,θ∈Θ为未知参数。

对θ进行区间估计，构造枢轴量T=T(X1,X2,…,Xn;θ)是样本 X1,X2,…,Xn和θ的函数，其分布密度为 g(x)，(g(x)与 θ无关)，分布函数。适当选择两个常数T1,T2，使对给定置信水平α(0＜α＜1)，有

假如能将T1≤T≤T2进行不等式等价变形化为a≤θ≤b，则

这时(a,b)就是未知参数θ的置信度为1-α的置信区间。

注意到满足（1）的T1,T2可以有很多，选择T1,T2的目的是希望（2）中的平均长度Eθ(b-a)尽可能短。

定义2使Eθ(b-a)达到最短时的参数θ的置信区间(a,b)称为θ的最短置信区间。

从定义可以看出，所谓最短置信区间就是寻找T1,T2，使Eθ(b-a)在满足（1）式条件下达到最小，属于条件极值问题。

定理1 若枢轴量T=T(X1,X2,…,Xn;θ)=Y(X1,X2,…,Xn)θ是单峰分布,x0为其峰点，且当x→0+,+∞时，g(x)→0，则参数θ的最短置信区间是存在且唯一的，且这时T1,T2满足：

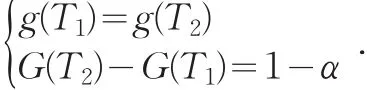
证明 因P(T1≤T≤T2)=1-α，所以

P(T1≤Yθ≤T2)=1-α，即

要使Eθ(b-a)最短，只要T2-T1最小。

又T=T(X1,X2,…,Xn;θ)的分布密度为 g(x)，分布函数为G(x)，所以

因此，最短置信区间问题就转化为条件极值：求T1,T2，使

成立。

利用Lagrange乘子法，令

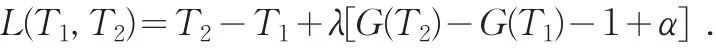
因为 T=T(X1,X2,…,Xn;θ)=Y(X1,X2,…,Xn)θ是单峰分布,x0为其峰点，且当x→0+,+∞时，g(x)→0，为保证T2＞T1且（3）式成立，必须

由引理，对任意满足（4）的T2，可以由（3）唯一地解出T1=u(T2),且T1是T2的单调减函数：

又注意到G(T2)-G(T1)=G(T2)-G(u(T2))是T2的单调增函数，且

故由中值定理，存在唯一的T2=T∗2,使G(T∗2)-G(u(T∗2))=1-α成立。

取T∗1=u(T∗2),则T∗1,T∗2是满足条件的T1,T2的唯一解。

定理2若枢轴量T=T(X1,X2,…,Xn;θ)=是单峰分布,函数x2g(x)在(0,+∞)内有唯一极大值点x0，且当x→0+,+∞时，x2g(x)→0，则参数θ的最短置信区间是存在且唯一的，且这时T1,T2满足：

类似定理1的证明。

对于常见分布，如正态分布，指数分布，伽玛分布等的参数的最短区间估计问题都可以由定理1,2找到相应的T1∗,T2∗及需满足的条件。

对于传统的置信区间，T1,T2的选取，只要满足

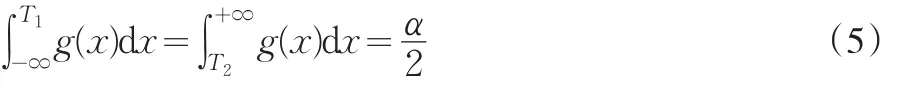
即按照概率对称的方式选取。由以上讨论可以看出，满足（5）的T1,T2一般不是达到最短置信区间的T∗1,T∗2；但是当枢轴量T的分布是正态分布，t分布等单峰对称分布，且未知参数θ位于枢轴量T的分子上时，二者是一致的。因为这时

是等价的。

实例 对正态总体N(μ,σ2)方差σ2进行区间估计。

所以x2g(x)在(0,+∞)内有唯一极大值点x0=n+1，且当x→0+,+∞时，x2g(x)→0。

因此，由定理2，参数θ的最短置信区间是存在且唯一的，且这时T1,T2满足：

这正是文[1]给出的结论。

鉴于解方程组(6)的复杂性，文[1]还制作了表格，找到T1,T2的近似值，方便查阅。并通过实例将最短区间与传统区间进行了比较，结果是对中小样本，二者差异显著；对大样本差异非常小。这是因为当样本容量n增大时，χ2(n)的分布密度关于其峰值的对称性在提高。所以，对于中小样本，研究未知参数的最短区间估计是很有必要的。

[1]王建华,张来成.正态总体方差的最短区间估计与最佳双边检验[J].数学的实践与认识,2003,33(2).

[2]袁长迎,徐明民.伽玛分布参数的最短置信区间[J].数理统计与管理,2006,25(4).

[3]钱瑛.单峰分布的置信区间[J].北京联合大学学报,1996,10(4).

[4]孙慧玲.取定统计量下的最优置信区间的估计[J].统计与决策,2009,(7).