可正定化矩阵的判别定理

陈恒新

(华侨大学数学科学学院,福建泉州 362021)

可正定化矩阵的判别定理

陈恒新

(华侨大学数学科学学院,福建泉州 362021)

对有关可正定化矩阵的理论做进一步的研究,给出有关可正定化矩阵的充分必要性定理.有关可正定化矩阵的主要判别定理是构造性的,即相关的对角阵D0,D＊是可由矩阵A的元素确定构造的.数值例子表明,定理具有较好的实用性.

可正定化矩阵;判别定理;充分必要性;构造性

对于解线性方程组Ax=f的许多迭代法,当系数矩阵A正定时的收敛性定理可直接推广到A为可正定化矩阵[1-4].关于可正定化矩阵,文献[1-2]从理论上进行研究,给出了一些相关定理及判定方法.然而,目前关于这一类问题的研究尚不够深入.为此本文对有关可正定化矩阵的理论做进一步的研究,给出了一些可正定化矩阵的充分必要性定理.

1 相关记号

为叙述简便,先引入如下记号.n阶实矩阵A=[ai,j];对角阵 D=diag(d1,d2,…,dn),若di>0,i= 1,2,…,n,则称D为正对角阵;集合N={1,2,…,n}.

2 可正定化矩阵的定义及判别定理

定义1 若存在对角阵 P和Q使PAQ为正定矩阵,则称A为可正定化矩阵.

由文献[1]的定理1,2可知有如下引理.

引理1n阶矩阵A是可正定化矩阵的充分必要条件是存在对角阵D,使DA为正定矩阵.

引理2n阶矩阵A是可正定化矩阵的充分必要条件是存在正对角阵D,使DA+为正定矩阵.

显然,由引理1,2可知有如下引理.

引理3n阶矩阵A是可正定化矩阵的充分必要条件是A+为可正定化矩阵.

由文献[3]的定理5,6可知有如下引理.

引理4 实对称矩阵A正定的充分必要条件是,它的所有顺序主子式det Ak>0,k=1,2,…,n.

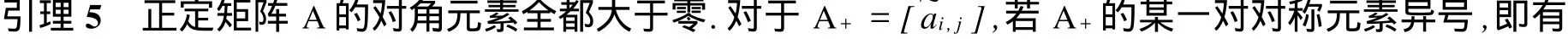
对任正对角阵D,DA+非对称;若不然,DA+为对称矩阵.因为 DA+=[di~ai,j],所以有=

显然,若的某一对对称元素不同时为零(即一个为零,另一个非零),则对任正对角阵D,DA+非对称.

若矩阵A有零对角元,则DA亦有零对角元.综上所述,由引理5及引理1,2可得如下定理.

定理1 若n阶矩阵A有零对角元或其A+的某一对对称元素异号或不同时为零,则A不是可正定化矩阵.

由引理3及定理1可知,判别n阶矩阵A是否为可正定化矩阵,只需考察相应的主对角元全为正的,且有如下所定义的矩阵.

定义2 若n阶矩阵A=[ai,j]的主对角元全为正,即ai,i>1,i=1,2,…,n,且A的对称元素ai,j与aj,i(i≠j),i,j=1,2,…,n同号或同时为零.即ai,j aj,i≥0且ai,j aj,i=0,当且仅当ai,j=aj,i=0,则记为A∈S+.

引理6 设n阶矩阵A=[ai,j]中存在某一个l∈N,使得al,j=aj,l≠0,j=1,2,…,l-1,l+1,…,n.若A不是对称矩阵,则对任非奇异对角阵D,DA不是对称矩阵.

证明 因为A是非对称矩阵,则必存在i0≠j0,使≠

于是有 D=diag(d,d,…,d),d≠0.因此,DA=[dai,j].由于 DA为对称阵,则有=故可得=与≠矛盾.

所以可知,不存在非奇异对角阵D,使DA为对称矩阵.证毕.又由已知有d1d2…dk>0,可知引理8成立.证毕.

定理2 设n阶矩阵A∈S+,且A=[ai,j]中存在al,j≠0,aj,l≠0,j=1,2,…,n(l为 N中的某一个数),则A为可正定化矩阵的充分必要条件是D0A为正定矩阵,而D0与引理7中 D0=diag(d1,d2,…, dn)所确定的对角阵相同.

证明 因A∈S+,可知D0为正对角阵,且矩阵A相应的A+=A.

充分性.若D0A为正定矩阵,由引理2可知A是可正定化矩阵.

必要性.若A是可正定化矩阵.

反证 假设D0A不是正定矩阵,则有下列2种情况.

(2)D0A为对称矩阵,但D0A不为正定矩阵.

由引理4可知,必存在某一个k,使det(D0A)k≤0,1,≤k≤n.因 D0为正对角阵,由引理8可知有det Ak≤0,1≤k≤n.但因A是可正定化矩阵,由引理2可知,必存在正对角阵D使DA+=DA为正定矩阵.于是,由引理4可知有det(DA)k>0,k=1,2,…,n.又由引理8可知有det Ak>0,k=1,2,…,n.这与det Ak≤0,1≤k≤n矛盾.即情况(2)亦不可能出现.因此,可知D0A为正定矩阵.证毕.

引理9 假设n阶矩阵A的三对角矩阵Atrd为两条斜对角线元素皆不为零的对称阵.即ai,i+1=ai+1,i≠0,i=1,2,…,n-1.若A不是对称矩阵,则对任非奇异对角阵D,DA不是对称矩阵.

证明 因A为非对称矩阵,则必存在i0≠j0,使ai0j0≠aj0i0.

于是有 D=diag(d,d,…,d),d≠0,故 DA=[dai,j].因为 DA为对称矩阵,则有dai0,j0=daj0,i0,由此可得ai0,j0=aj0,i0与ai0,j0≠aj0,i0矛盾.所以可知,不存在非奇异对角阵 D使DA为对称矩阵.证毕.

其次,若ai,i+1≠0,ai+1,i≠0,i=1,2,…,n-1中ai,i+1·ai+1,i>0,则 D＊为正对角阵.

据引理9,10及相关引理,完全类似定理2的证明,便有下列定理.

定理3 设n阶矩阵A∈S+,且A的三对角矩阵Atrd中两条斜对角线元素皆不为零,即ai,i+1≠0, ai+1,i≠0,i=1,2,…,n-1.则A是可正定化矩阵的充分必要条件,D＊A为正定矩阵.其中:D＊同引理10中 D＊=diag(d1,d2,…,dn)所确定的对角阵.

3 数值例子

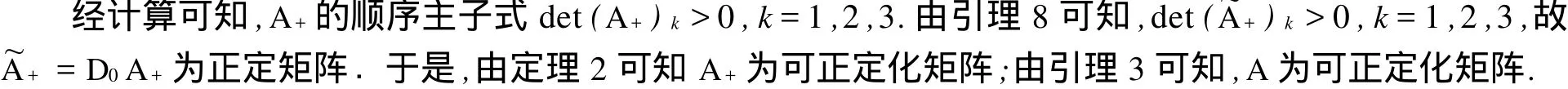
[1]王伟贤,王志伟.关于可正定化矩阵的判定[J].数值计算与计算机应用,1999,20(3):215-222.

[2]胡家赣,刘兴平.EPEk方法和可正定化矩阵[J].数值计算与计算机应用,1997,18(1):30-39.

[3]蒋尔雄,高坤敏,吴景琨.线性代数[M].北京:人民教育出版社,1978.

[4]陈恒新.关于非负矩阵Perron特征值的上、下界[J].应用数学与计算数学学报,2007,21(1):1-8

(责任编辑:陈志贤英文审校:张金顺,黄心中)

Criteria theorem of Positive-Definable Matrix

CHEN Heng-xin
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

Theory of the positive-definable matrix be further studied.The necessary and sufficient theo rem s for the positive-definable matrix are given in the paper.These theorem s have better uses than the present critical theorems,that is, the co rrelated diagonal matrix D0,D＊in our theorem s can be structured determinately by the elements of the matrix A. For this reason,it has good practical value.Four numericial examples are given here,that show s these theorems had better practical uses.

positive-definable matrix;critical theorem;necessity and sufficiency;structure

O 241.6

A

1000-5013(2011)03-0356-05

2009-12-16

陈恒新(1956-),男,副教授,主要从事计算数学和数值代数的研究.E-mail:chenhx@hqu.edu.cn.

福建省自然科学基金计划资助项目(S0650018)