计算非负不可约矩阵谱半径的新算法

宋海洲,徐强,田朝薇

(华侨大学数学科学学院,福建泉州 362021)

计算非负不可约矩阵谱半径的新算法

宋海洲,徐强,田朝薇

(华侨大学数学科学学院,福建泉州 362021)

设A=(ai,j)n×n为非负不可约矩阵,设计一种计算非负不可约矩阵谱半径ρ(A)的通用迭代算法,并证明算法的收敛性.数值实验表明,该算法比幂法迭代算法具有较快的收敛速度.

正矩阵;谱半径;迭代方法;收敛性

非负矩阵在数值分析、图论、计算机科学、控制论、管理科学等领域上有着极其重要的作用[1-4],而非负矩阵谱半径的计算又是其核心问题之一.计算非负矩阵的谱半径,通常采用幂法、正交三角矩阵(QR)算法,但这些算法迭代速度不快.本文设计一种计算非负不可约矩阵谱半径的通用迭代方法.

1 算法的设计

设A=(ai,j)n×n为非负不可约矩阵,则迭代计算谱半径ρ(A)的算法有如下4个步骤.

(4)若W2,k-W1,k>ε,更新R=maxiri(C),转步骤(3);否则,令(W1,k+W2,k)/2为矩阵 A的近似谱半径.

2 算法的收敛性

引理1[5]设B为正矩阵,X=(x1,x2,…,xn)T为 B对应ρ(B)的正特征向量,Y=(y1,y2,…, yn)T为BT对应ρ(B)的正特征向量.令c=(YTX)-1,则有

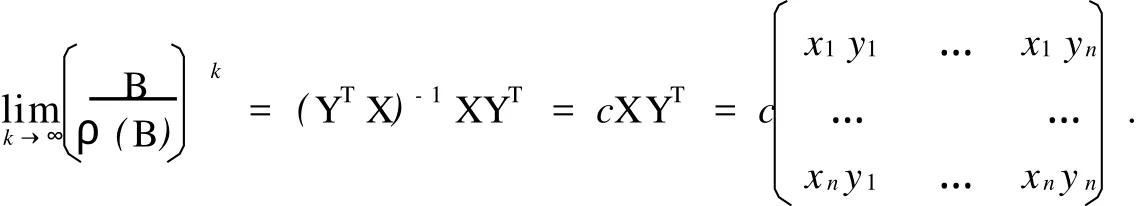
定理1 设B为n阶正矩阵,X=(x1,x2,…,xn)T为B对应ρ(B)的正特征向量,记为Bk的第i行行和(i=1,2,…,n),记u1=…,n,并且有

证明 设Y=(y1,y2,…,yn)T为BT对应ρ(BT)的正特征向量,记c=(YTX)-1.由引理1,有

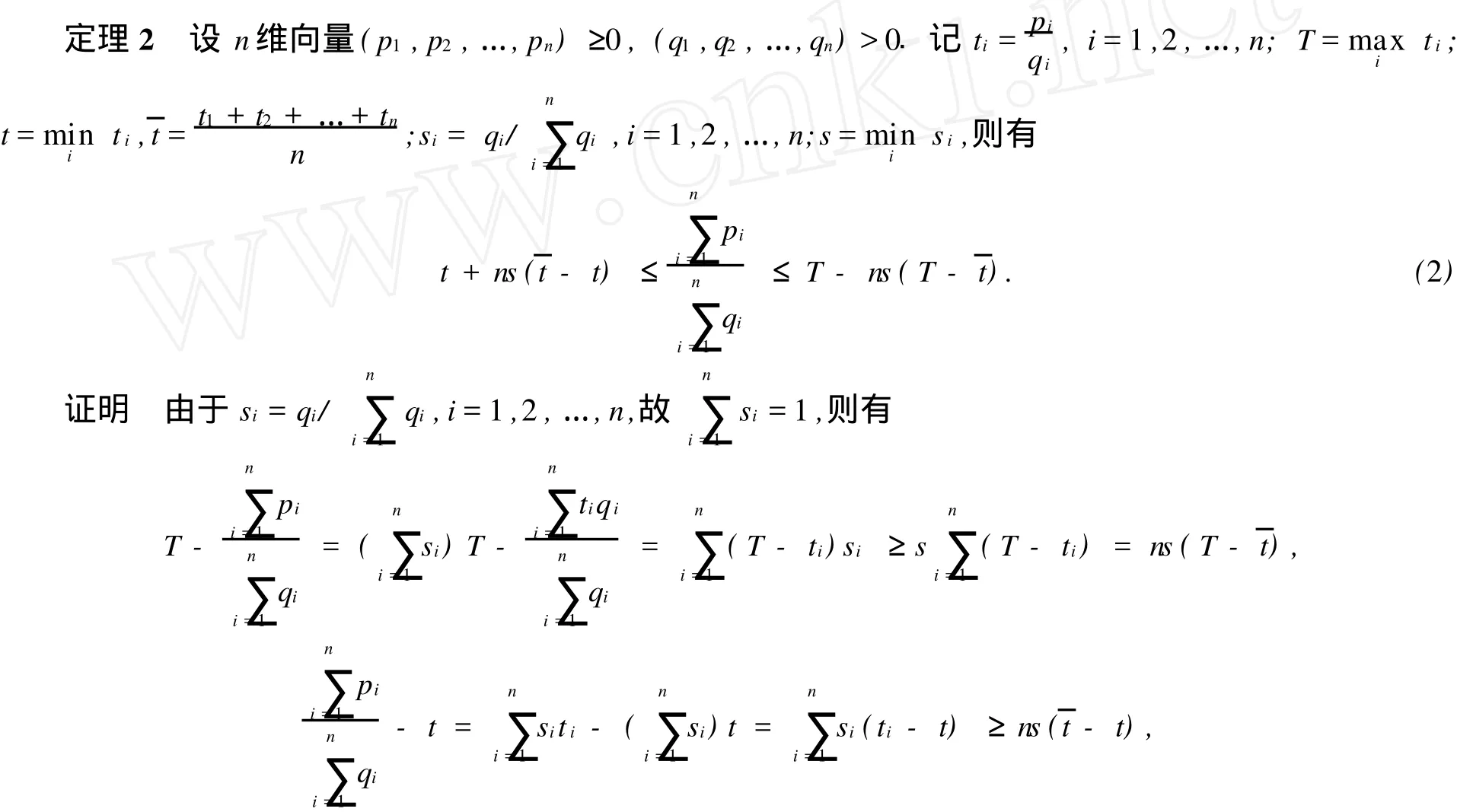
由此可证式(2)成立.证毕.

引理2[5]设A为n阶非负不可约矩阵,B=(A+I)n-1,则B为n阶正矩阵.

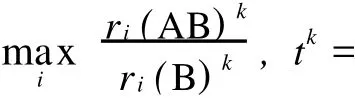
定理3 设B=(bi,j)是n阶正矩阵,记ri(Bk)表示Bk的第i行行和(i=1,2,…,n,k=0,1,…=bi,m rm(Bk)(i,m=1,2,…,n;k=0,1,…),

证明 假设 X=(x1,x2,…,xn)T为B对应ρ(B)的正特征向量,则由定理1可得,对于任意i,m= 1,2,…,n,有

又因为对于任意i,m=1,2,…,n,任意k=0,1,2,…,有>0,故s=inf|k=0,1,…,i;m= 1,2,…,n}>0.

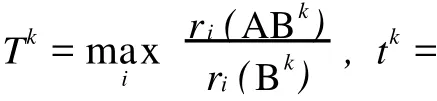
证明 易知AB=BA,故由Tk及tk的定义及引理4可得

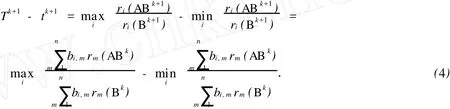
再利用定理3,可得

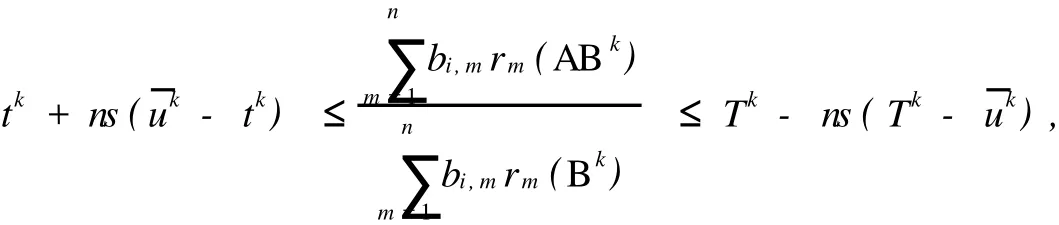
利用上式及式(4),可得

由定理3可知,1-ns<1,而1-ns≥0是显然的,故|1-ns|<1.利用上式递推,可得

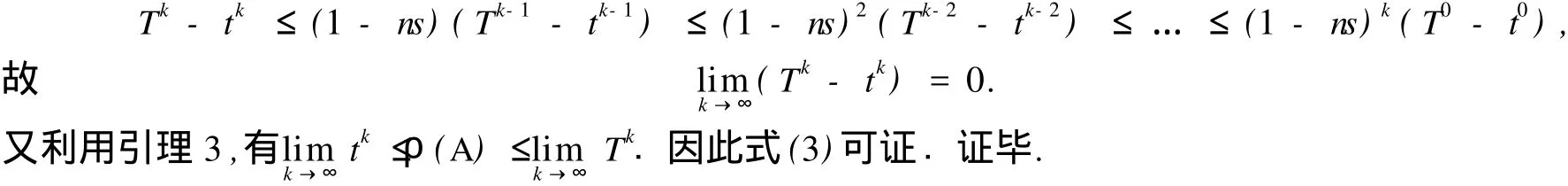
3 数值试验

由非负不可约矩阵的算法求得的结果,如表1所示.

表1 例1中矩阵A的谱半径表Tab.1 Table of matrix A′s spectral radius in examp le 1

对于例1中的矩阵A,采用幂法是求不出ρ(A)的.

采用幂法及非负不可约矩阵的算法,求A的谱半径在精度要求下所需的迭代次数,如表2所示.

表2 例2矩阵A的谱半径的收敛速度比较表Tab.2 Table for the convergence rate comparison of matrix A′s spectral radius in examp le 2

从表2可以看出,所设计求非负不可约矩阵的算法比幂法收敛速度要快.

[1]卢琳璋,马飞.非负矩阵perron根的上下界[J].计算数学,2003,25(2):58-64.

[2]殷剑宏.非负矩阵最大特征值的新界值[J].数值计算与计算机应用,2002,23(4):292-295.

[3]段复建,张可村.Z-矩阵最小特征值及特征向量的数值算法[J].2007,24(3):563-566.

[4]张凤祥.非负矩阵最大特征值的平滑算法[J].高等学校计算数学学报,2001,23(1):45-55.

[5]蒋正新,施国梁.矩阵理论及其应用[M].北京:北京航空学院出版社,1998.

(责任编辑:陈志贤英文审校:张金顺,黄心中)

A New Algorithm for the Spectral Radius of Non-Negative Irreducible Matrix

SONG Hai-zhou,XU Qiang,TIAN Zhao-w ei
(School of Mathematical Sciences,Huaqiao University,Quanzhou 362021,China)

Let A=(ai,j)n×nis a non-negative irreducible matrix,then a new algorithm for the spectral radiusρ(A)of the matrix A is designed in this paper.The convergence of the algorithm is also proved.It is show n that the algorithm has a rapid convergence rate by numerical experiment.

non-negative;irreducible;iterative method;convergence

O 241.6

A

1000-5013(2011)03-0348-04

2009-07-11

宋海洲(1971-),男,副教授,主要从事数学模型的研究.E-mail:hzsong@hqu.edu.cn.

福建省自然科学基金资助项目(Z0511028)