采用统一强度理论的锚喷支护围岩弹塑性统一解
郑强,林从谋,孟凡兵
(华侨大学岩土工程研究所,福建泉州 362021)
采用统一强度理论的锚喷支护围岩弹塑性统一解
郑强,林从谋,孟凡兵
(华侨大学岩土工程研究所,福建泉州 362021)
基于双剪统一强度理论,结合点锚式锚杆锚喷支护的力学机理,导出双向等地应力情况下无限均匀介质中锚喷支护圆形洞室围岩应力场、位移场及塑性区半径解析解.分析强度理论参数b值对弹性区和塑性区应力、位移的分布特点的影响,以及锚喷支护对塑性区半径影响的变化趋势.结果表明:与Morhr-Coulomb强度理论结果相比,隧道轴向应力和强度理论中的参数b对隧道围岩应力场、位移场、塑性区半径及支护反力等均有影响;围岩应力值在锚固区外端位置有一个跌落;锚固区外端在塑性区的围岩应力跌落比在弹性区时大,隧道围岩塑性区半径随着锚固区半径先增大而减小,最后趋于平缓.
弹塑性;锚喷支护;统一强度理论;围岩
在地下结构(如巷道、隧道)中,都存在围岩变形及围岩与支护结构相互作用问题.一方面,当洞室周围锚有均布的径向锚杆时,都能通过承拉限制围岩径向位移来改善围岩应力状态,而且通过锚杆承剪可改善锚固体力学参数,提高锚固体的强度,形成共同承载结构,充分发挥围岩自承能力[1].另一方面,岩石的强度及破坏不仅与最大主应力、最小主应力有关,还与中间主应力密切相关,实验证实中间主应力可使岩石的强度增大30%左右[2].目前,在隧道等地下结构的弹塑性分析中,通常采用Mohr-Coulom b强度理论、Hoek-B row n强度理论等单剪强度理论[3-4].然而,该强度理论忽略了中间主应力的作用,只考虑最大和最小主应力对材料强度的贡献,导致分析结果普遍偏于保守.双剪统一强度理论[5-7]是一种对于拉压同性和异性,不同中间主应力效应情况下都可以适用的强度理论,并可以退化成或线性逼近于其他的各种强度理论.本文基于考虑中间主应力影响的统一强度理论,结合隧道锚喷支护对围岩稳定性的影响,推导围岩中基于统一强度理论锚喷支护的统一解.
1 双剪统一强度理论
双剪统一强度理论的表达式[5-7]为
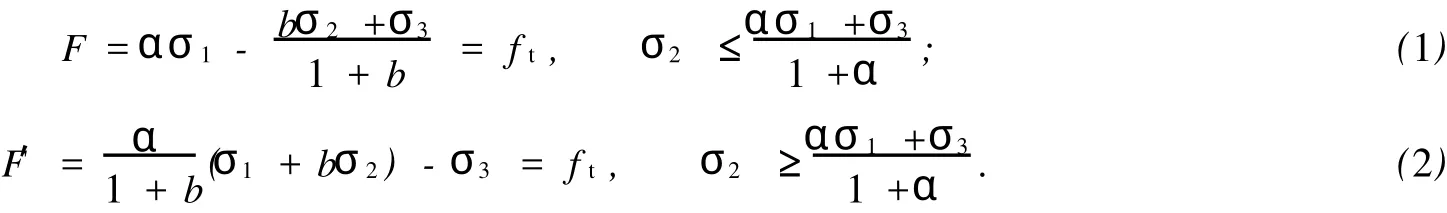
式(1),(2)中:b为强度理论参数;α为材料单轴强度抗压比;ft为材料的单轴抗拉强度.
从上两式可看出,统一强度理论融现有的各种强度理论于一体,已不是传统意义上的,只适用于某一类材料的单一强度理论.如果采用单剪强度理论,就只能考虑到隧道断面上径向应力和切向应力的作用;而采用统一强度理论,不仅可以考虑到上述两个应力,还可考虑到隧道轴向应力的作用[6-8].
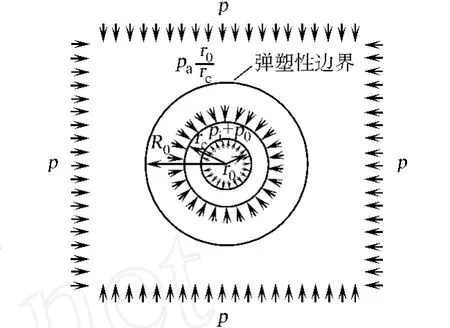
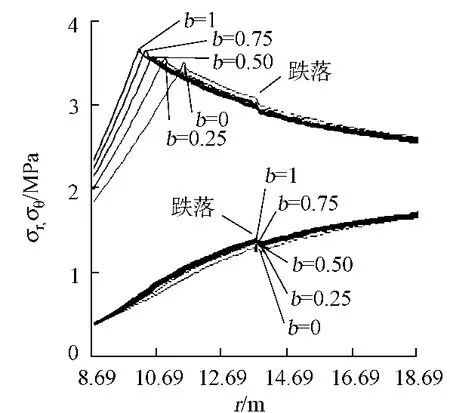
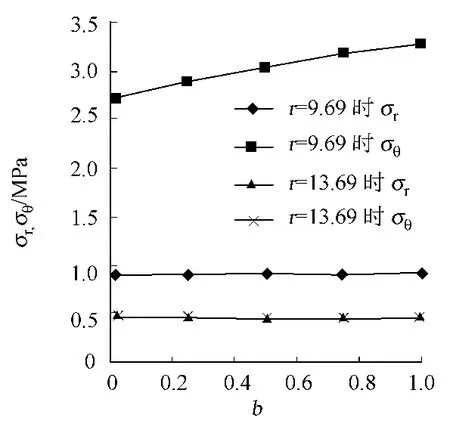
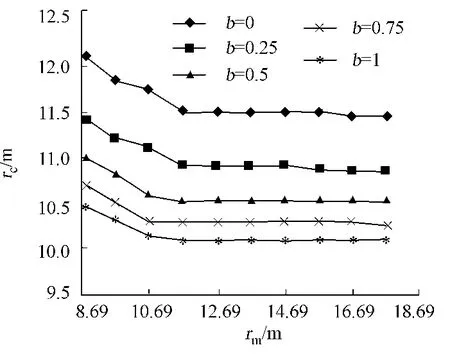
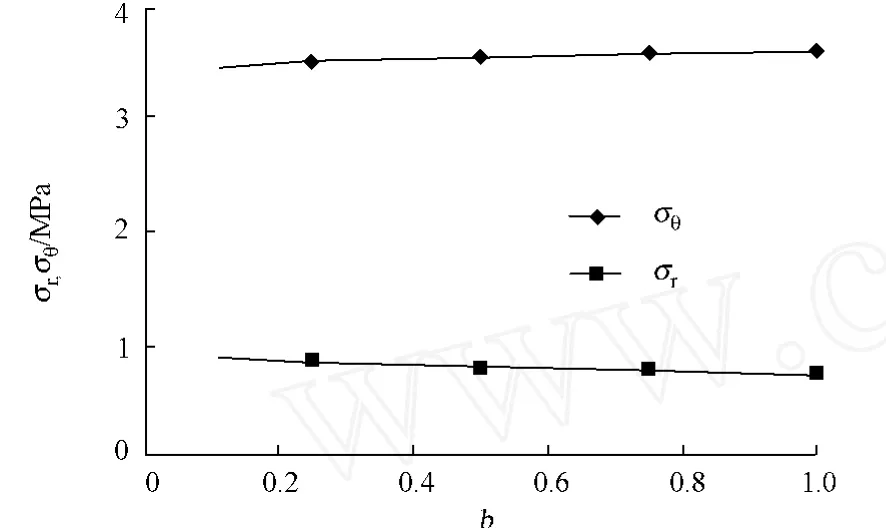
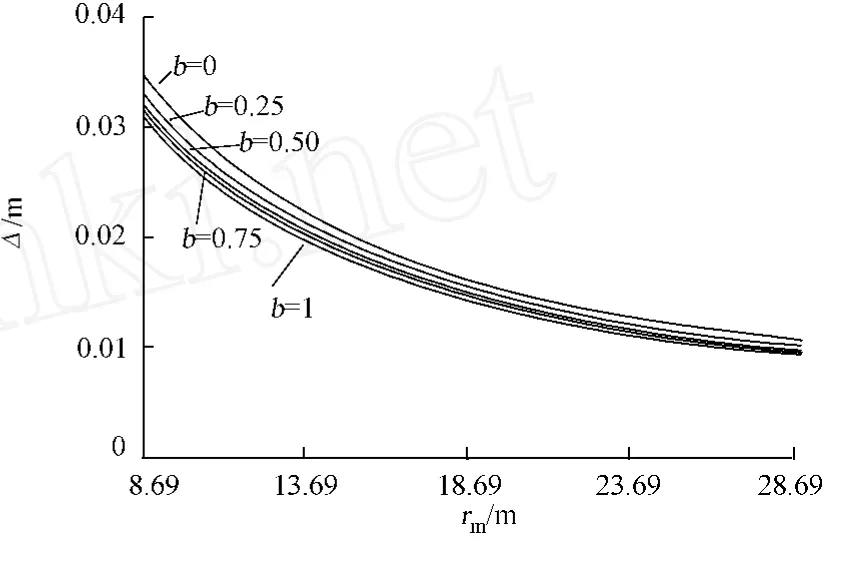
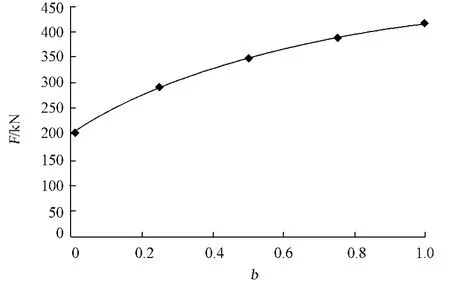
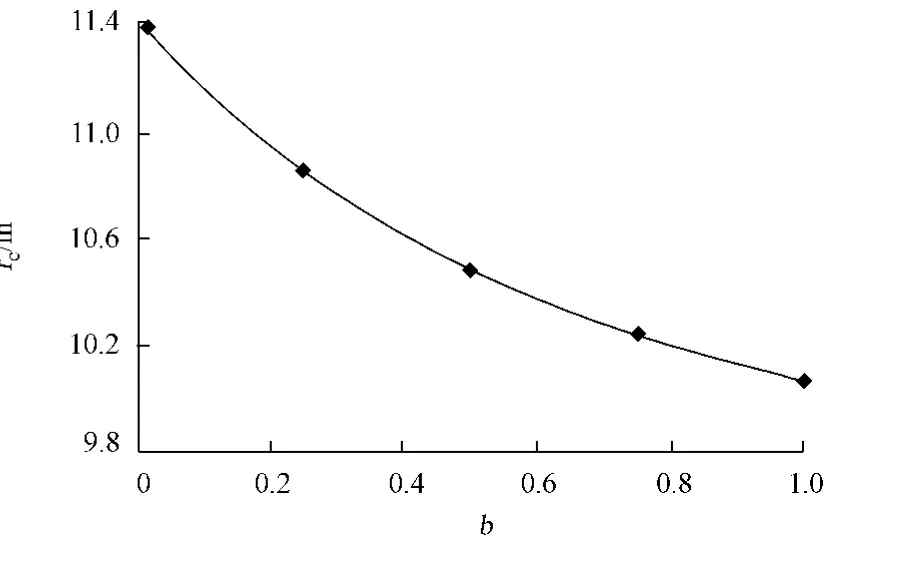
对于外凸型强度理论而言,b的取值范围为[0,1].当b=0时,统一强度理论退化成 Mohr-Coulomb强度理论,它界定了统一强度理论的下限;当b=1时,统一强度理论退化成双剪强度准则,它界定了统一强度理论的上限;当0 图1 力学计算模型Fig.1 Mechanical model 静水压力条件下,圆形断面隧道围岩的弹塑性力学分析可以看成是平面应变问题,并可以认为是主应力.塑性区内的径向应力、切向应力和轴向应力的关系为 不考虑体积力时,平面应变问题的平衡方程为 当边界条件r=r0时,锚杆在洞壁上产生支护的附加抗力=pa+pi,将式(4)代入式(5),可得 式(6)中:rc为有锚杆时的塑性区半径. 塑性区边界r=rc处的应力与原岩应力p的关系为 将式(7)代入塑性条件式(4),经整理后即可得r=rc处的应力为 式(8)表明:弹塑性界面的应力是一个取决于p,C1,φ1的函数,与支护抗力pa,pi无关. 令锚杆内端点的径向应力为σm并位于塑性区内,则在弹塑性界面上的径向应力为 由此可得 此外,由式(4)并考虑锚杆内端的分布力,有 联立式(10),(11),可得有锚杆时的塑性区半径rc,即 将式(12)代入式(6),(7),可得洞壁到锚杆内端区域内的应力解析解,即 将式(11)代入式(6),(7),可得锚杆内端到弹塑性边界区域内的应力解析解,即 锚固区内弹性区的弹性应力为 弹塑性边界条件为 在无穷远处有 围岩弹性区应力及位移为 式(20)中:rc≤r≤+∞. 为求得塑性区位移up,可假定小变形情况下塑性体积不变,即ε==0.将几何方程代入,可得 该微分方程的解为 式(22)中:A为待定系数.由弹塑性界面r=rc上变形协调,有 令弹塑性界面上的应力差为M,由式(8)可得 将弹性区及塑性区位移表达式代入(23),可得 因而,可得有锚杆时的塑性区围岩位移,即 对于点锚式锚杆,按锚杆与围岩共同变形理论获得锚杆轴力,有 式(27)中:u′为锚杆外端位移;u″为锚杆内端位移为锚固前的洞壁位移,原则上应按实测值确定,也可按经验确定;Ea,As分别为锚杆弹性模量与锚杆横截面面积. 塑性区的应力解和位移解同上.锚固区内弹性区的弹性应力为 锚固区外弹性区的弹性应力为 由弹塑性边界条件=可得 在无穷远处,有=+∞==+∞=p,C′=p/2.由两弹性区界面=+∞=p,可得 两弹性区位移协调后可得 联立后可得 弹塑性边界和两弹性区边界分别为 因而,塑性区位移为 锚固区内和锚固区外弹性区位移分别为 实例A 8合同段大帽山隧道为泉厦高速公路扩建隧道,扩建方案在原两洞之间新建一座4车道隧道,并将右洞扩建为4车道,形成大断面小间距隧道群.隧道洞身最大埋置深度约为110 m,转化为等代圆[9]后,r0=8.69 m,rc=13.69 m,C=0.2 M Pa,φ=30,p=2.12 M Pa,pi=0.3 M Pa,G=210 M Pa.经计算,锚固外端位于弹性区内,故采用锚杆锚固端位于弹性区内的计算公式,结果如图2~8所示. 图2 轴向(或径向)应力与半径的关系Fig.2 Relationship between axial(o r radial)stress and the radius 图3 应力下降值与参数b的关系Fig.3 Relationship between stress drop and parameter of b 图4 塑性区与锚固区半径的关系Fig.4 Relationship between plastic zone radius and anchor radius 图5 参数b对轴向(或径向)应力的影响Fig.5 Parameters b influence on Influence on axial(o r radial)stress 图6 围岩位移与半径的关系Fig.6 Relationship between displacement and radius for different b values 图7 参数b与锚杆轴力的关系Fig.7 Relationship between anchor axia force and parameters of b 图8 参数b与塑性区半径的关系Fig.8 Relationship between parameter b and plastic zone radius 由图2,3可以看出,围岩应力值在rm位置有一个跌落,其中的下降值为(r0/rm)pa的下降值.当锚杆锚固外端在围岩塑性区时下降显著,切向应力下降值为锚固端压力的2.5~3.5倍,径向应力下降值为锚固端压力的1.0~1.5倍.这主要是由围岩极限平衡条件中的C,φ值决定;当锚杆锚固外端在围岩弹性区时下降减小,切向应力和径向应力下降值相等,为锚固端压力的1/3~1/4. 由图4可以看出,隧道围岩塑性区半径rc随着锚杆锚固区半径rm增加开始阶段显著减小,呈双曲线函数关系;到一定阶段后,rc基本无变化,呈近水平直线变化.在围岩塑性区半径处,锚杆长度稍微增加锚固到弹性区时,可充分发挥围岩体的承载能力,rc有适当减小.因此,合理、经济地选择锚杆长度,可以有效地控制围岩塑性区在较小的范围内. 由图2~8可以看出,围岩径向应力随着参数b的增大而增大;切向应力在塑性区随着参数b的增大而增大,在弹性区则随着参数b的增大而减小;塑性区半径和隧道周边围岩径向位移随着参数b的增大而减小;弹塑性交界处的围岩径向应力及切向应力均随着参数b的增大而增大. (1)采用统一强度理论分析的锚喷支护围岩弹塑性结果,不仅包含了以往基于Mohr-Coulomb理论等结果,并给出一系列新的结果,适用于多种的材料.(2)参数b对隧道围岩应力场、位移场、塑性区半径及支护反力等均有影响,因此,在隧道弹塑性分析中合理选择参数b具有重要的意义. (3)隧道围岩塑性区半径随锚固区半径先增大而减小,之后呈近水平直线变化;在围岩塑性区半径处,锚杆长度稍微增加锚固到弹性区时,可充分发挥围岩体的承载能力. (4)围岩应力值在锚固端位置有一个跌落,当锚杆锚固端在围岩塑性区时下降显著,切向应力下降值为锚固端压力的2.5~3.5倍,径向应力下降值为锚固端压力的1.0~1.5倍;当锚杆锚固端在围岩弹性区时下降值减小,切向应力和径向应力下降值相等,为锚固端压力的1/3~1/4倍. [1]叶明亮.地下结构围岩锚固参数的弹塑性分析[J].贵州工业大学学报:自然科学版,1998,27(1):71-77. [2]许东俊,耿乃光.岩石强度随中间主应力变化规律[J].固体力学学报,1985,6(1):72-80. [3]于学馥,郑颖人,刘怀恒,等.地下工程围岩稳定分析[M].北京:煤炭工业出版社,1983. [4]王抒,张顶立.隧道软弱围岩相似材料的力学性能试验[J].华侨大学学报:自然科学版,2010,31(6):680-683. [5]俞茂宏.岩土类材料的统一强度理论及其应用[J].岩土工程学报,1994,16(2):1-10. [6]俞茂宏.双剪理论及其应用[M].北京:科学出版社,1998. [7]宋俐,张永强,俞茂宏.压力隧洞弹塑性分析的统一解[J].工程力学,1998,15(14):57-61. [8]胡小荣,俞茂宏.统一强度理论及其在巷道围岩弹塑性分析中的应用[J].中国有色金属学报,2002,12(5):1021-1026 [9]李世辉.隧道支护设计新论[M].北京:科学出版社,1999. (责任编辑:钱筠英文审校:方德平) Elastic-Plastic Unified Solution of Shotcrete-Anchorage Support Surrounding Rock Based on Unified Strength Theory ZHENG Qiang,L IN Cong-mou,M ENG Fan-bing Combining the mechanical mechanism of point ancho red bolts and twin shear unified strength theory,rock stress field of surrounding,displacement field and analytical solution of plastic zone radius in circular tunnel are educed under the two-way stress in an infinite homogeneous medium,the influence of the parameterbvalue of strength theory on the features of stress and displacement distribution in the elastic and plastic zone are analyzed.Furthermore,the trend of anchor support influence on radius of plastic zone is analyzed.It′s show n that the tunnel axial stress and the parameterbof strength theory affect tunnel surrounding rock stress field,disp lacement field,p lastic zone radius and support reaction etc;the stress value of surrounding rock drops in the outside end of anchorage zone,also surrounding rock stressoutside of anchorage in the plastic zone drops more than that in the elastic zone;with increasing the anchorage area radius,the plastic zone radius of tunnel surrounding rock increases initially,then decreases,finally almost doesn′t change. plastic;shotcrete-anchorage support;unified strength theory;surrounding rock U 451.2 A 1000-5013(2011)03-0326-06 2010-12-12 林从谋(1957-),男,教授,主要从事岩石动力学和地下结构的研究.E-mail:cm lin@hqu.edu.cn. 福建省科技计划重点项目(2007H0055);福建省自然科学基金资助项目(2006J0445)2 力学计算模型建立
3 锚固圈位于塑性区内
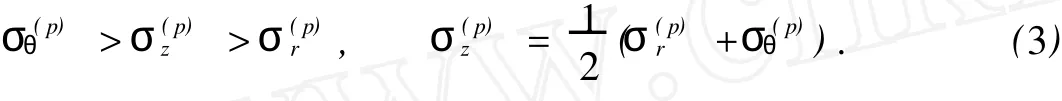
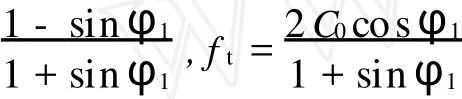

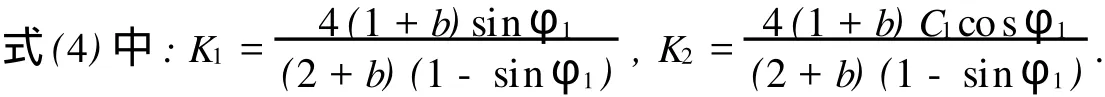



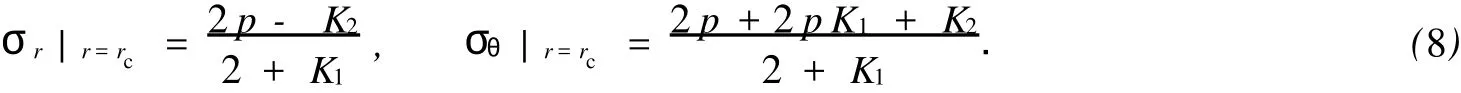
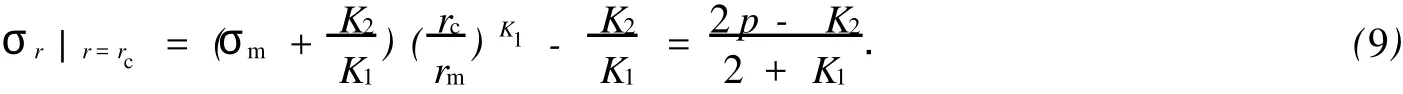
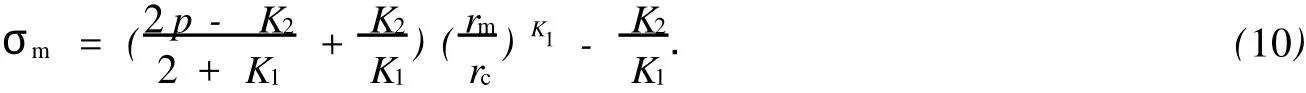
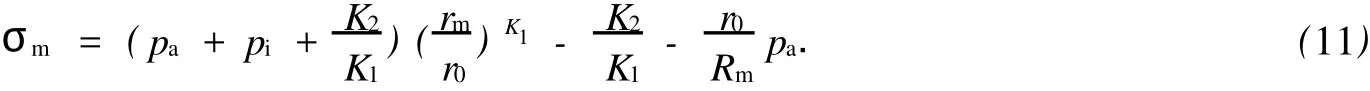
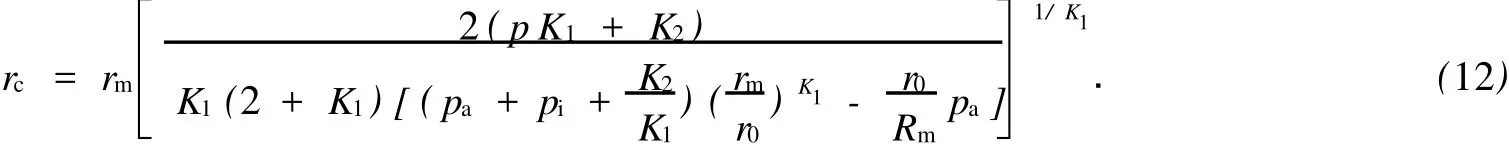
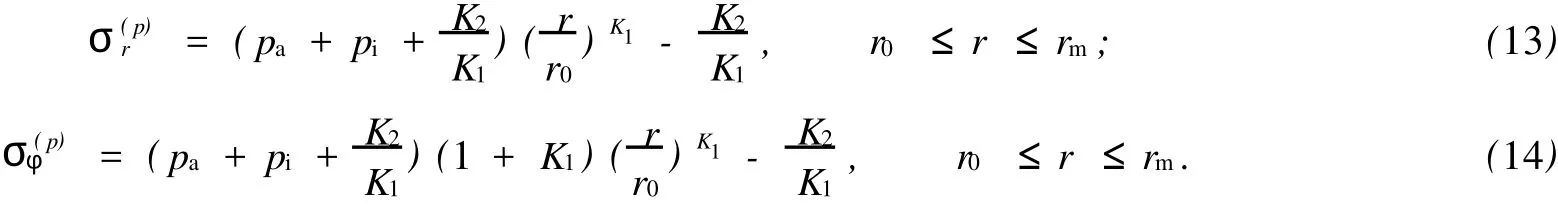
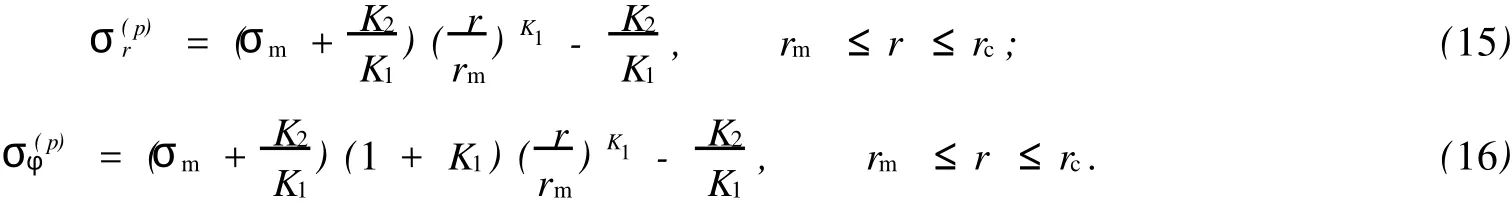
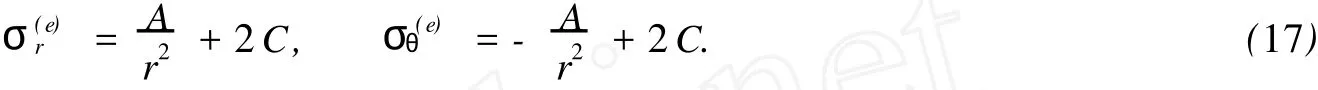
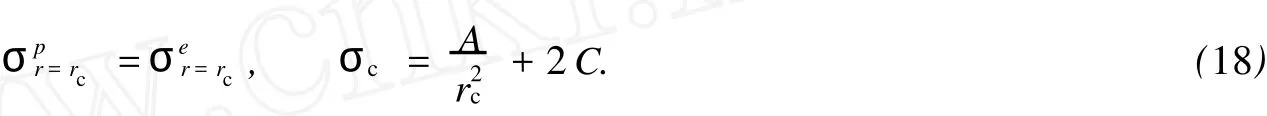

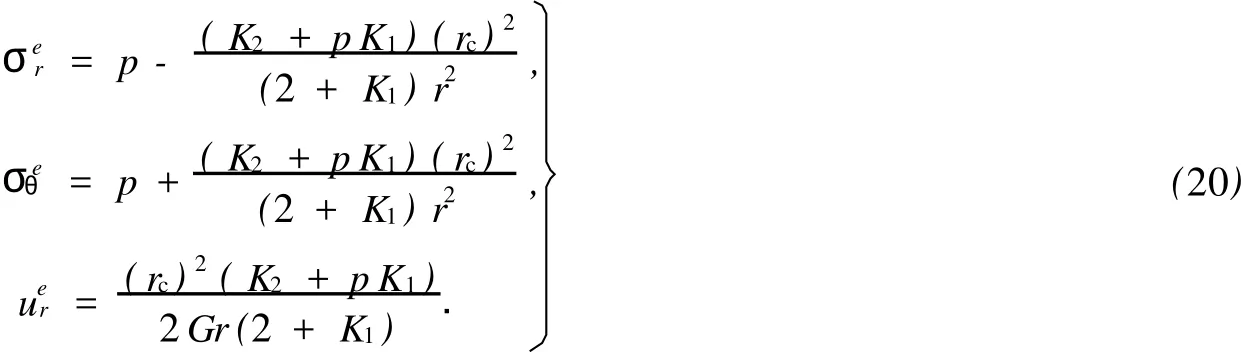



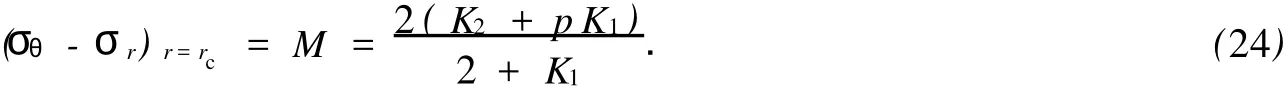
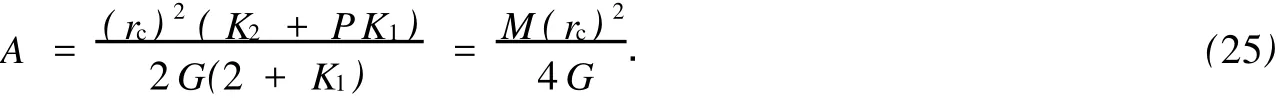
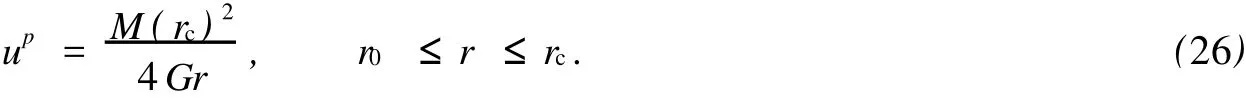
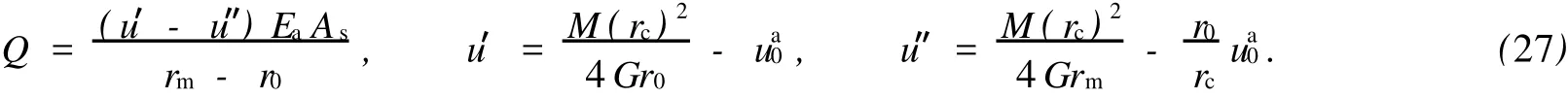
4 锚杆锚固端位于弹性区内
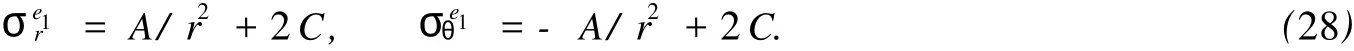




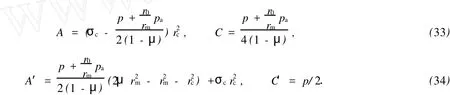
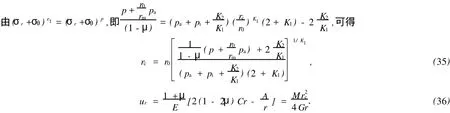
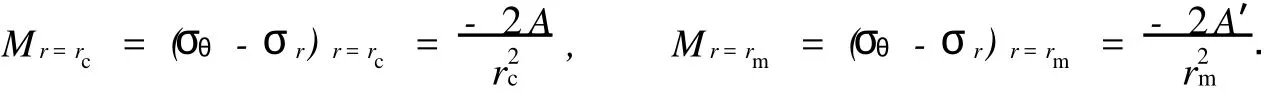

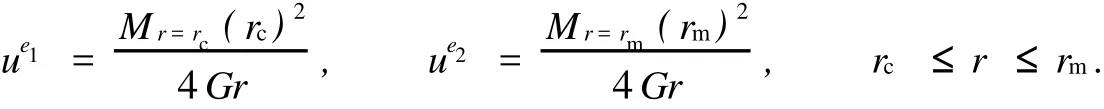
5 工程实例分析
6 结论
(Research institute of Geotechnical Engineering,Huaqiao University,Quanzhou 362021,China)

