关于平方根整数部分的一个恒等式的推广

管 训 贵

(泰州师范高等专科学校 数理系，江苏 泰州 225300)

关于平方根整数部分的一个恒等式的推广

管 训 贵

(泰州师范高等专科学校 数理系，江苏 泰州 225300)

设 a,b 都是正整数.本文证明了：对不小于的?正整数 m,n，若

平方根；整数部分；恒等式；推广

1 引言及主要结论

对于实数a，用[a]表示不超过a的最大整数．显然0≤a＜1时，有[a]=0．这是数论及其相关领域的一个重要函数，许多数学工作者曾对此有过大量的研究[1]．比如，Gauss就曾通过有关有理数整数部分的一个恒等式证明了数论中著名的“二次互反律”[2]．

对大于2的正整数n和非负整数m，设

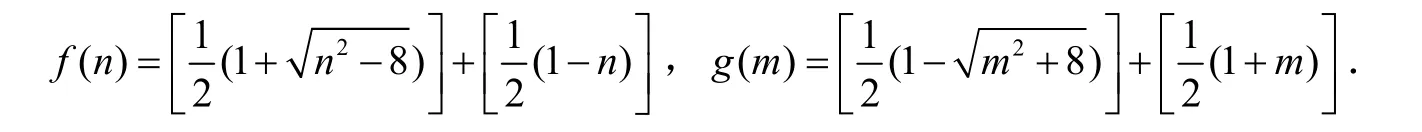
最近，Bencze M[3]对此提出了以下问题：对于任意的n(n≥3)和m(m≥0)是否都有f(n)=g(m)？乐茂华[4]证明了：当n≥3且m≥0时，如果n≠4且m≠2，则必有f(n)=g(m)=0．

本文将这一问题进行推广，得到了如下结果：

则必有f(n)=g(m)=a -1．

2 关键性引理

3 定理证明

结合(1)与(4)及引理，我们有：

(Ⅰ) 若a,n同奇同偶，则

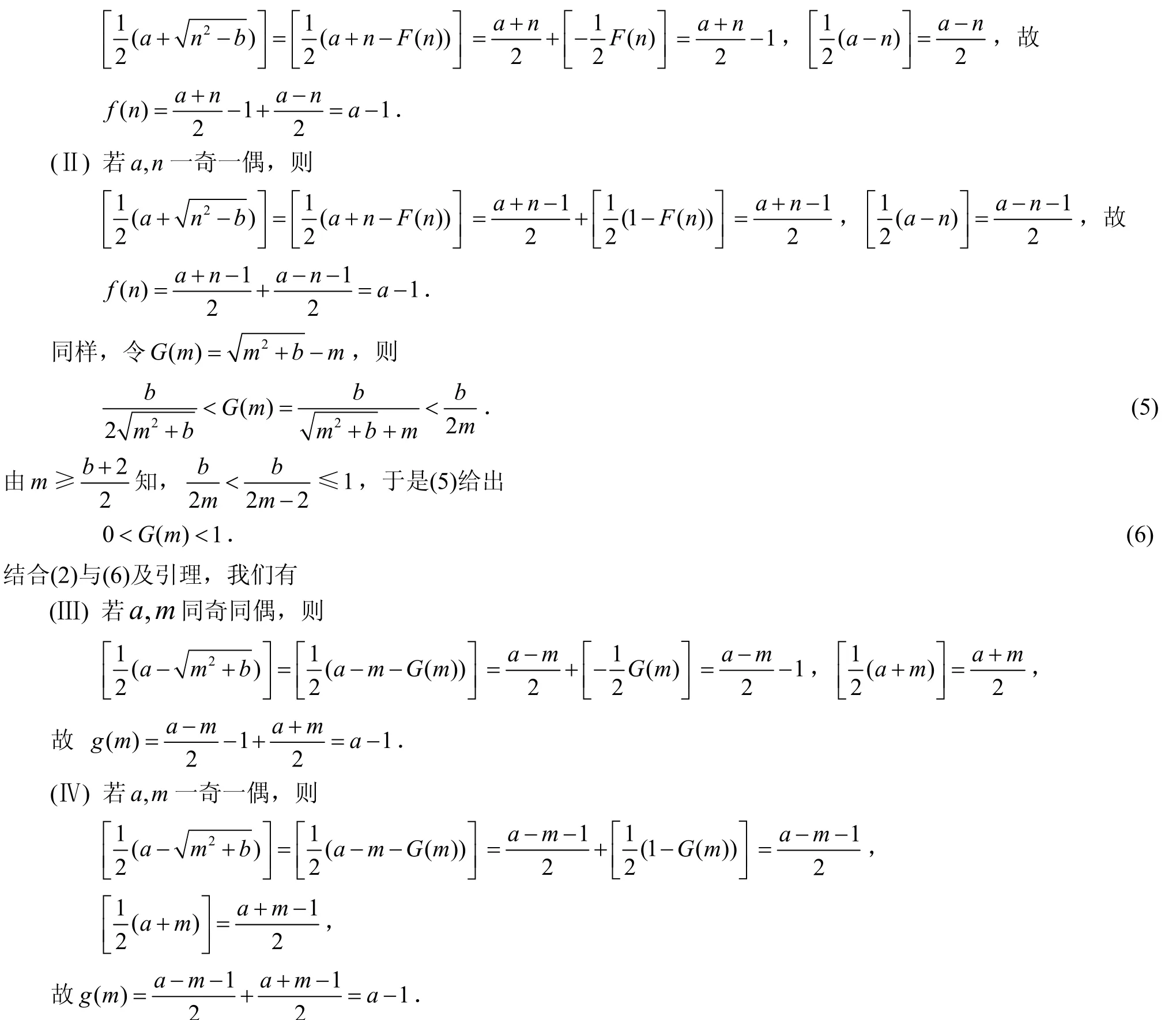
由(Ⅰ)～(Ⅳ)知，定理得证．

[1] DICKSON L E. History of the theory of numbers:Vol I [M]. Washington:Camegie Institution,1919:106-138.

[2] BACHMANN P. Niedere Zahlentheorie [M]. Leipzig:Teubner,1910:75-89.

[3] BENCZE M. Proposed problem 8869[J]. Octogon Math.Mag,2005,13(2):1172.

[4] 乐茂华.关于平方根整数部分的一个恒等式[J].衡水学院学报,2007,9(1):41-42.

Abstract:Let a and bare positive integers. In this paper we prove that for any positive integers m and n , withthenf(n)=g(m).

Key words:square root; integral part; identity; generalization

(责任编校：李建明英文校对：李玉玲)

Generalization for the Identity on the Integral Parts of Square Roots

GUAN Xun-gui

(Mathematics ＆ Physics Department of Taizhou Normal College, Taizhou, Jiangsu 225300, China)

O156

A

1673-2065(2011)01-0010-02

2010-09-12

泰州师范高等专科学校重点课题资助项目(2009-ASL-042)

管训贵(1963-),男,江苏省兴化人,泰州师范高等专科学校数理系副教授.