爆炸磁频率发生器电感特性分析

索 莹 邱景辉 李 伟 袁业术

（哈尔滨工业大学电子与信息工程学院，黑龙江 哈尔滨 150001）

1.引 言

利用非核手段产生电磁脉冲破坏探测、通讯及指挥系统已成为各国研究的热点之一［1-3］。电磁脉冲可覆盖很宽的频率范围，且具有较高的瞬时能量，可对电子系统造成巨大威胁，因此，对于电磁脉冲的研究在基础理论和技术领域有重要的应用。爆炸磁频率发生器（explosive magnetic generator of frequency，EMGF）是一种结构紧凑的一次性电磁脉冲产生和辐射装置，最早在文献［4］中由Prishchepenko提出，之后国内外做了大量的实验研究。这种发生器具有结构简单、体积小、功率大等优点，在很多领域有广阔的应用前景，引起各国的广泛关注［5］。

爆炸磁频率发生器是一种将炸药的化学能转化为电枢的动能，并进一步转化为系统的电磁能量的装置，其结构上与早期报道的磁通量压缩发生器（explosive magnetic flux compression generator，FCG）基本相同［6］，区别在于在发生器末端的串联电容，电容的加入改变了发生器回路电流特性，从而覆盖很宽的频率范围（频率范围覆盖几十兆赫兹到上百吉赫兹），如果将此电磁脉冲通过天线有效辐射出去，将具有重要的应用价值。发生器正处在不断完善中，虽然辐射机理还存在一定争议，但从等效电路角度分析，发生器中存在频率足够高的振荡电流是产生电磁辐射的基础［7］。

这里首先从等效电路分析，研究电感的变化规律对磁频率发生器工作电流信号特性的影响，接着从实际模型出发，探讨对有电枢存在时的电感计算进行修正，并通过实验的方法验证爆炸磁频率发生器产生脉冲辐射的可能性。

2.发生器等效电路模型

爆炸磁频率发生器由螺旋型FCG发展而来，即由缠绕于电枢外的定子线圈串联一小电容构成，结构简图如图1所示，当电枢在炸药爆炸的作用下依次扩张，与定子的各匝线圈依次短路，则线圈内的磁场被压缩，由于定子线圈的电感不断减小，根据磁通量守恒原理，使得电流强度越来越高，又根据ω=（LC）0.5，回路电流信号的振荡频率会越来越高，最终导致在短时间辐射出一定强度的电磁脉冲。

爆炸磁频率发生器的等效电路如图2所示，其中C1表示提供初始电流的大电容；C2为在回路中产生振荡频率的小电容；L（t）为磁通量压缩发生器的电感线圈；R1表示电路电阻（包括全部磁通量损失和电路电阻）；R2为连接于变压器的次级线圈的复杂负载。

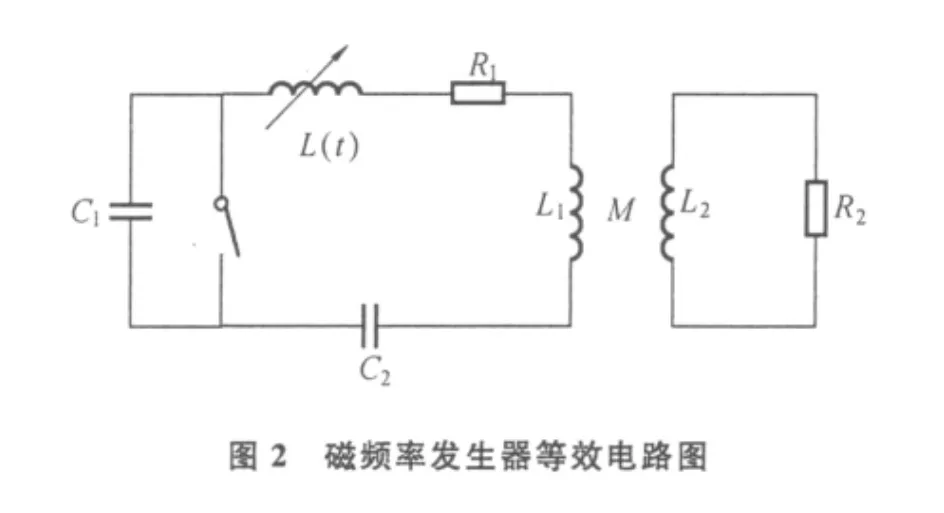
当充电回路电流达到最大值时，撬杆开关与电枢接触，充电回路被短路，若直接与大电阻负载连接，初始能量将在极短的时间内传送至负载电阻，发生器中的磁通量还未得到压缩，因此，能量无法实现转换，因此，需要考虑通过变压器连接大电阻负载。此处在分析等效电路时，暂时忽略变压器对回路的影响，并且不考虑回路中的杂散电容和引线产生的分布电感，根据基尔霍夫定律电压守恒，图2中回路电流的等效电路初始方程为

整理后，得到回路的等效电路方程为

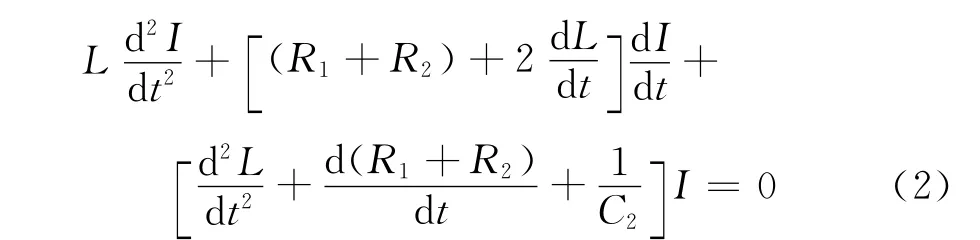
当电感的变化形式及初始条件确定，就可得到工作电流I（t），通常情况下，电流I（t）的解析解是很难求出的，这里采用数值解法求解方程。随着爆炸的进行，电感线圈不断减小，因此，L′（t）＜0，按照电感缠绕方式的不同，电感减小的方式可分为3类［8］，一种为电感线性减小（L″（t）=0），另一种为电感减小先慢后快（L″（t）＜0），最后一种为电感减小先快后慢（L″（t）＞0），并根据现有的实验条件，给出一组实际的初值，得出各自条件下，回路电流的工作情况。

首先考虑电感线性减小的情况，即L=L0（1-t／τ），τ为电感放电时间。则可得到工作回路的微分方程为

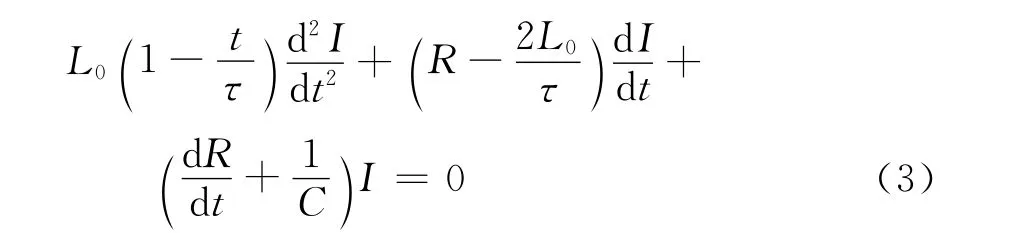
取L0=1μH，R=0.02Ω，C=500pF，τ=20 μs，通过求解微分方程，得到工作电流的时间变化曲线如图3所示，电流的振幅在运行结束时迅速变大，而频率也有所升高，但从电流的频域谱中看，中心频率在70MHz左右，电流达到半功率频带约为60～90MHz，但频率和振幅的增加都在发生器运行的最后阶段，仅占发生器运行时间的10%，不利于电磁振荡的有效辐射。

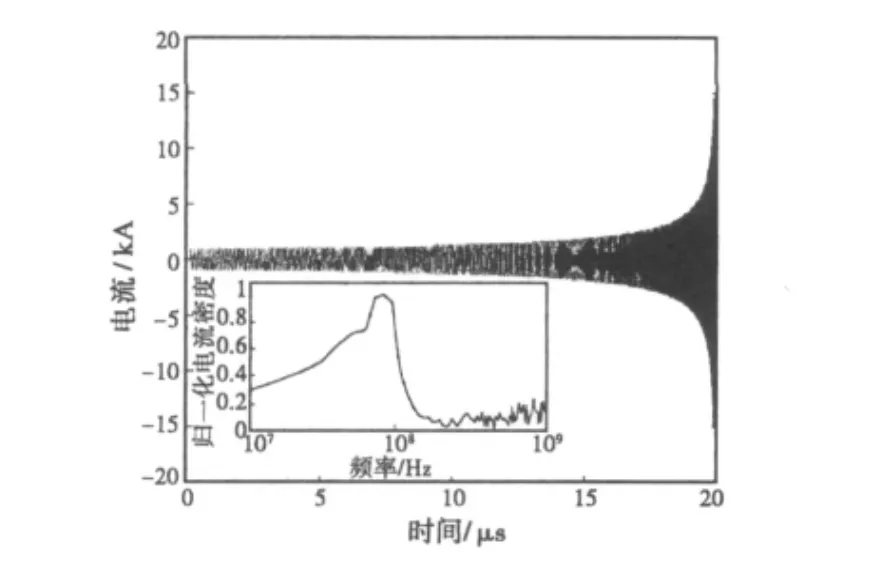
图3 电感线性变化时电流特性曲线

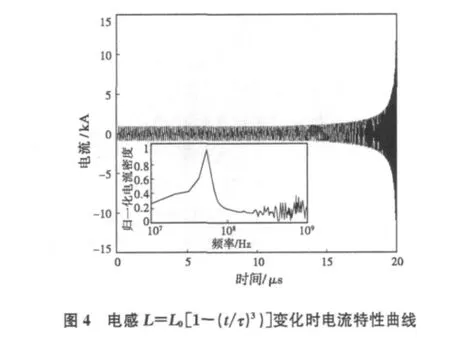
对于第二种情况，电感减小先慢后快的形式，在电阻足够小的情况下，电路中电流波形的包络也是时间的增函数，这与图3类似，在临近爆炸结束阶段，增加变得极为迅速，电流的增加可以认为是理想状态下磁通量有保持不变的趋势，并且电感的减小需要电流的增大来补偿，另外，电感的减小带来了电流振荡频率的增加。但若电感不断减小过程中满足上述条件，则电感线圈的螺距应为先疏后密，但在电感减小的后期，由于电流的增加，过密的螺距使得线圈之间击穿的概率增大，也为发生器的设计增加了难度，因此，此类情况不适于发生器的工作。以L=L0［1-（t／τ）3）］为例，仍取L0=1μH，R=0.02Ω，C=500pF，τ=20μs，通过求解微分方程，得到工作电流的时间变化曲线如图4所示，中心频率仍在50 MHz左右，半功率频带宽度变窄，约15MHz.

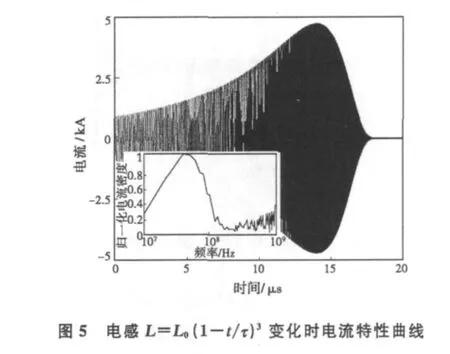
第三种情况是电感减小先快后慢，即L″（t）＞0，以L=L0（1-t／τ）3为例，仍取L0=1μH，R=0.02 Ω，C=500pF，τ=20μs，电流的计算结果见图5，电流的时间包络呈鱼形，约在5μs时，电流频率开始上升，电流在爆炸后期（约17μs时刻）迅速衰减，这与文献［4］中吻合较好。电流达到半功率频带约为20～90MHz，带宽得到有效扩展，若对参数进行优化，有进一步扩展带宽的可能性，更有利于电磁辐射。

以上从等效电路的角度对发生器进行分析，重点分析了螺线管电感的变化率对工作电流的影响，从系统中存在频率不断增长的电流振荡信号验证了产生电磁辐射的可能性，至于线圈自身产生的辐射，以及爆炸过程中产生的高温等离子体对发生器造成的影响都有待深入的研究。

3.动态电感分析

爆炸过程中，电感的精确计算对电容放电时间、电流放大倍数以及频谱的计算有很大影响，在发生器运行过程中，电感随着爆炸的进行不断变化，需要建立动态电感的变化模型。当电感螺距随时间变化时，现有的电感计算公式无法精确计算电感值，因此，会把线圈视为环形电感的串联形式，则初始电感可表示为

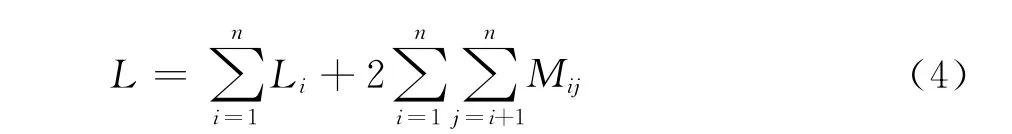
式中:Li为各圆环电感的自感；Mij为第i，j个圆环间的互感。因此，可通过计算出线圈随时间t消失变化的匝数n（t），得到电感的变化公式。对于圆环电感，在30～300MHz频率范围内，自感约为［9］

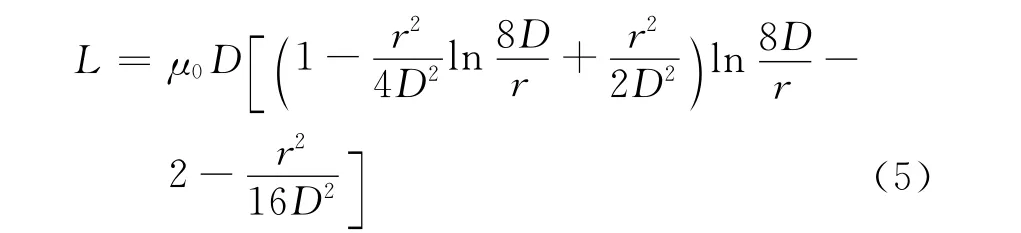
式中:D为圆环线圈半径；2r为线径。当线圈绕匝不是很密，螺线管不是很长的情况下，互感可表示为

式中，Kij，Eij分别为kij的第一类。第二类全椭圆积分。至此可得到螺旋线圈的电感值，但是此类计算研究是按照空心螺旋线圈计算的，发生器的线圈里放置有电枢，当电流在线圈中传递，电枢的导电壁产生涡流，从而使电枢形成一个电磁屏，因此，计算电感时应考虑电枢的影响，即不考虑屏蔽时求出的电感值（L和M）与电枢屏蔽影响产生的增量电感（ΔL和ΔM）之和。当电枢与线圈如图1放置时，由电枢屏蔽作用产生的自感增量以及线圈间的互感增量分别为

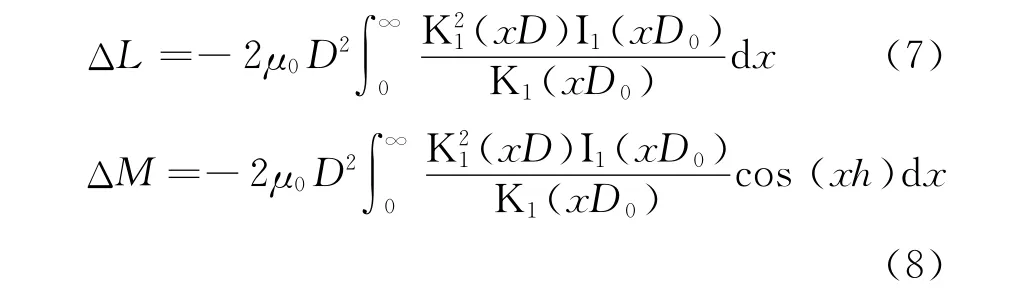
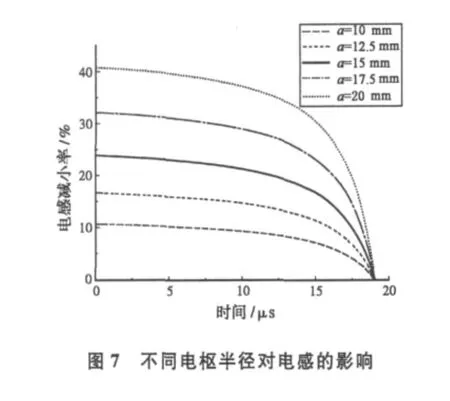
式中:h为线圈螺距；I1，K1分别为第一类和第二类一阶修正贝塞尔函数。以电感线性变化为例，选择螺旋线圈半径25mm，线圈螺距10mm，电枢长20cm，半径15mm，则线圈半径为电枢半径的1.67倍，电枢内填充炸药的爆炸速度为10km／s.分别计算不考虑电枢屏蔽作用和综合考虑电枢屏蔽作用时的电感变化曲线，计算结果如图6所示，考虑电枢屏蔽作用的初始电感减小为原来的76%，影响较大，随着爆炸向前推进，电枢的屏蔽作用影响逐渐减弱，但整个过程中电枢的屏蔽作用不可忽略。线圈到电枢的距离直接影响电感大小，保持上述其他参数不变，仅改变电枢半径a从10mm到20mm，则可得到电枢的屏蔽作用使得电感的减小率计算结果如图7所示，模型的电感线圈螺距不变，因此，计算相对简单，影响的趋势很明显，随着电枢半径的减小，电感的减小量就越小，并且随着时间的推进，屏蔽作用对电感减少率的影响逐渐减弱，直到爆炸结束。

4.实验验证

根据现有条件，实际制作了一个爆炸磁频率发生器，发生器线圈按照先密后疏的方式分为三段缠绕，其参数见表1。发生器的结构如图8（a）所示，左边为螺旋型磁频率发生器，可以利用罗科夫斯基线圈进行测量得到工作回路中的电流，右边是为线圈提供初始电流的电容器。由于磁通压缩运行过程是复杂的磁流体运动现象，而且实验中存在多种损耗以及加工工艺产生的跳匝现象，使得磁通量压缩与预计的结果有一定的误差。由于发生器爆炸过程中对周围电磁环境有很大影响，示波器检测到的波形有一定的失真，图8（b）给出了由罗科夫斯基线圈测量得到的电压结果，经过转换得到工作回路的电流，幅度大约放大18倍，频率约为初始频率的1.5倍。实验结果证明发生器产生电磁辐射的原理是可以实现的，但要达到国际先进水平，还需要对结构和加工工艺进行进一步的改进与提高。

表1 发生器线圈主要参数

5.结 论

对螺旋型爆炸磁频率发生器基本模型的电感特性进行了详细的理论研究，从等效电路出发，通过分析不同电感变化率得到了相应的电流特性曲线，结果表明:电感减小先快后慢的变化规律结构更合理，有利于电磁辐射。接着结合发生器结构，考虑电枢存在下电感的计算，得到修正后的电感计算公式，并得出电枢半径不同时，电感减小率与时间的变化曲线，提高了发生器电感计算的精确度。实验结果证明了该类型发生器能够产生振荡电流，并最终产生电磁辐射。本文中电感变化特性的分析对爆炸磁频率发生器的应用研究有一定的指导意义，电感计算的修正对发生器的设计也有一定的参考价值。下一步的工作是在实验中产生上百兆赫兹甚至几百吉赫兹的电磁辐射，并进行更深入的研究。

［1］LV Q A，LEI B，GAO M，et al.Magnetic flux compression generator as future military pulsed power supply［J］.IEEE Transactions on Magnetic.2009，45（1）:545-549.

［2］PARKER J V，CAVAZOS T C，ROTH C E，et al.Development and testing of a high-gain magnetic flux compression generator［C］∥ Proceedings of 11th International Conference on Megagauss Field Generation and Related Topics.London，2006:265-274.

［3］姜泽辉，赵海发，曲 伟，等.爆炸磁频率发生器的等效电路分析［J］.电波科学学报.2005，20（2）:193-196.JIANG Zehui，ZHAO Haifa，QU Wei，et al.Equivalent circuit analysis for explosive magnetic frequency generators［J］.Chinese Journal of Radio Science，2005，20（2）:193-196.（in Chinese）

［4］ПРИЩЕПЕНКО А Б， ЩЕЛКАЧЕВ М В.Диссипативныеидиффуэионныепотеривспиральном взрывомагнитном генераторе. Электричество ［J］.1993:31-36.

［5］DAVIS C B，NEUBER A A，YOUNG A，et al.Optimization of an FCG-based high-power microwave system using nonexplosive pulsed power［J］.IEEE Transactions on Plasma Science.2009，37（12）:2321-2327.

［6］NOVAC B M，SMITH I R.Brief History and classification of magnetic flux compression generators［J］.E-lectromagnetic Phenomena.2003，3（3）:358-365.

［7］ALTGILBERS L L，ONOOCHIN V V.Analysis of the equivalent circuit of prishchepenko-type spiral MCGs［C］／／12th IEEE International Pulsed Power Conference，1999:1260-1263.

［8］姜泽辉，吴 冬，韩杰才，等.电感变化率对爆炸磁频率发生器性能的影响［J］.电波科学学报，2007，22（6）:924-927.JIANG Zehui，WU Dong，HAN Jiecai，et al.Influences of inductance reducing rate in explosive magnetic frequency generators［J］.Chinese Journal of Radio Science，2007，22（6）:924-927.（in Chinese）

［9］卡兰塔罗夫著.电感计算手册［M］.陈汤铭译.机械工业出版社.1992:250-256.