散射波干扰对合成孔径雷达成像干扰效果的分析

刘业民 刘 忠 代大海 王雪松

(国防科学技术大学电子科学与工程学院，湖南 长沙 410073)

1. 引 言

合成孔径雷达(SAR)是一种利用天线运动形成综合孔径对地面目标实现二维成像的有源微波雷达[1]。在环境监视、海洋观测、资源勘探和测绘等方面的应用具有独特的优势，特别是在军事侦察领域上具有重大的使用价值。

对SAR的有源干扰大致可分为压制干扰和欺骗干扰两种[2]，有源压制干扰主要是通过对SAR发射非相干信号(如常规射频噪声等)来降低SAR图像的对比度，从而达到保护目标的目的，其不足是需较高的干扰功率；有源欺骗干扰包括转发式干扰和应答式干扰，这种干扰形式可以在干扰能量有限的情况下形成虚假干扰目标，从而有效地保护真实目标。但是，采用该干扰形式需要利用电子侦察手段精确测知对方发射信号的形式，同时还要精确测得SAR到干扰机的相对位置[3]，这对干扰机硬件成本要求较高。上述的有源干扰方法均采用的是直达波干扰形式，而文献[4][5]提出了一种新思路的有源干扰方法，即散射干扰方法，它与常规的直达波干扰不同，它并不直接向雷达发射或转发干扰信号，而是接收雷达发射的信号并形成干扰相参脉冲串，将其投射到需要进行干扰的区域，经地物散射以后形成地物干扰回波与雷达原始回波信号混合在一起被雷达接收，从而破坏雷达对地物目标的识别。由于散射波干扰方法只改变了原雷达信号的传播路径，因而其干扰信号与距离向滤波器是完全匹配的，与方位向滤波器是完全或者部分匹配的，因此，所需的干扰功率比压制干扰少得多[6]，而且克服了上述有源欺骗干扰方法中存在的不足。另外，散射波干扰可以对SAR图像产生以下三种可能的干扰效果：1)虚假图像欺骗干扰；2)散焦图像压制干扰；3)虚假图像欺骗干扰+散焦图像压制干扰。

目前已有不少文献对散射波干扰方法进行了相关的研究，文献[7]提出了一种改进的SAR散射波欺骗干扰方法，通过对干扰信号的调制以及利用方位向频率调制系数，可对SAR形成更逼真的欺骗干扰效果；文献[8]从双站散射特性的角度分析了散射波干扰方法中双站散射后问题的必要性和复杂性；文献[9]通过对散射波信号进行距离向延时和方位向相位补偿，实现对散射波欺骗场景干扰；文献[10][11]分别研究了散射波干扰方法对双基地SAR的干扰效果；对于产生三种干扰效果的条件，目前还未进入深入的研究，为此，文章从散射波干扰方法对SAR干扰效果的研究为出发点，深入分析了这种干扰方法对SAR产生上述不同的干扰效果所需的干扰条件。文章分为三部分：首先在分析散射波的干扰原理基础上，提出了散射波干扰因子；接着分析了散射波干扰方法对SAR在距离向和方位向的干扰效果，进而给出了对SAR形成虚假图像欺骗干扰和散焦图像压制干扰所需的干扰条件；最后就机载SAR和星载SAR进行了散射波干扰仿真实验，仿真结果验证了理论分析的正确性。

2. 干扰原理

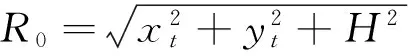
Rj(ta)=Rrj(ta)+Rjt+Rtr(ta)

(1)

式中：

(2)

分别为载机到干扰机的瞬时斜距和载机到目标的瞬时斜距，Rjt为干扰机到目标的斜距。

对星载SAR和机载SAR而言，一般情况下，都有R0≫|x-xt|，Rj0≫|x-xj|，在此条件下，则式(2)有以下近似(Fresnel近似)[12]。

(3)

把式(3)代入式(1)，求得干扰信号回波的多普勒中心频率fDcj和多普勒调频率fRj分别为

(4)

式中：λ为波长；α为散射波干扰因子

(5)

根据式(5)可知，散射波干扰因子α与θj成反比，与干扰机高度h成正比。一般而言，对SAR进行散射波干扰时，其干扰机一般位于SAR波束照射的区域附近，其θj变化不大，因而干扰机高度h的变化是影响α变化的主要因素，且α≥1.

另外，SAR方位向匹配滤波器的多普勒中心频率fDc值和多普勒调频率fR值分别是[13]

(6)

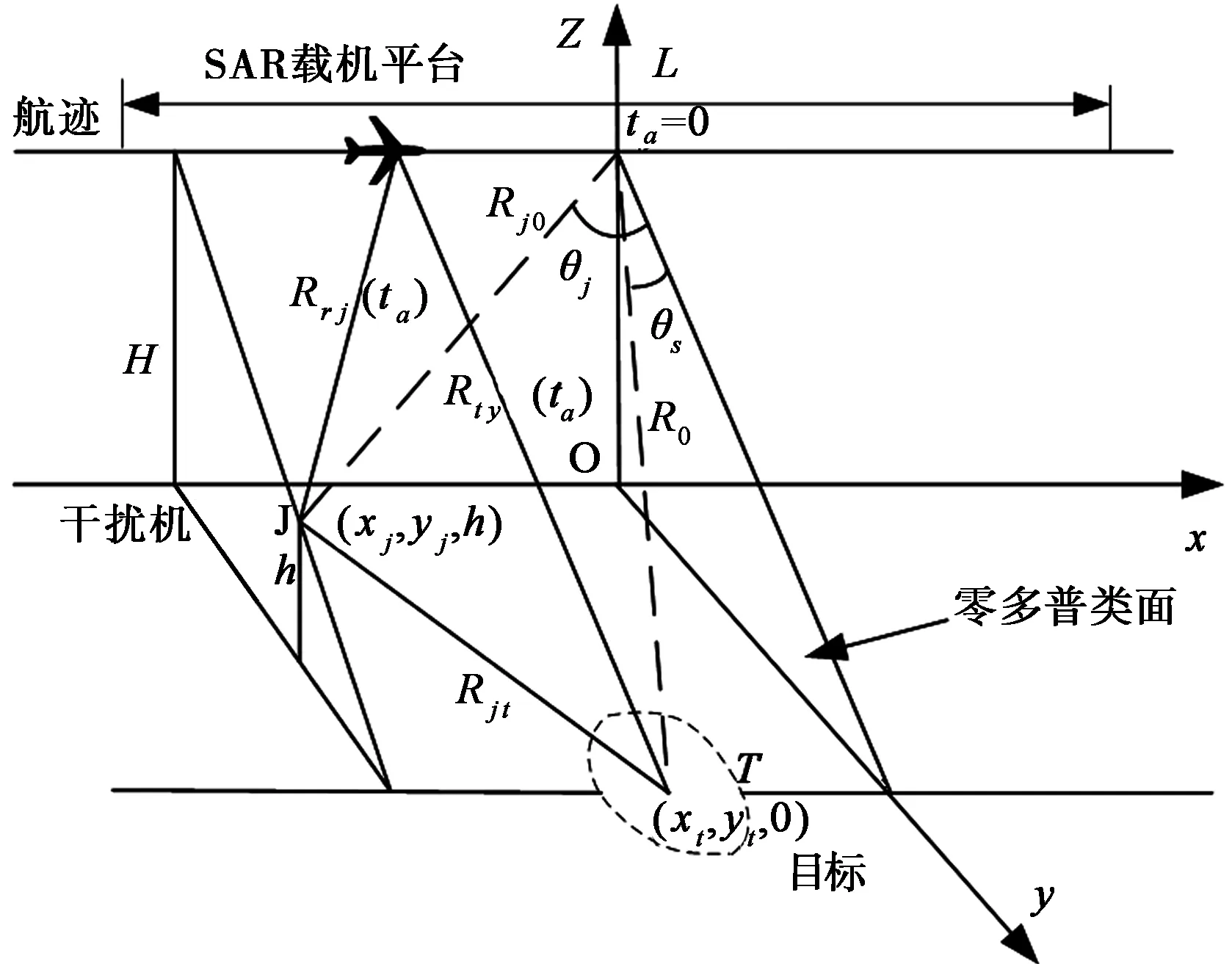
图1 散射波干扰原理图

由式(4)～式(6)可知，干扰信号回波与匹配滤波器之间存在着多普勒参数的失配，多普勒中心频率失配仅仅会引起信噪比的损失和增加模糊度，但多普勒调频率失配会引起不可接受的方位分辨率损失(即散焦)[13]。文章主要考虑多普勒调频率失配对SAR图像的干扰效果，为此，定义多普勒调频率的失配率

(7)

从式(7)可以看出：散射波干扰因子α变大，多普勒调频率的失配率|δfR|亦变大。

3. 干扰效果分析

3.1 距离向干扰效果分析

假设SAR发射的信号为线性调频信号，其信号形式为

(8)

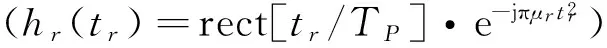
sj(tr,ta) =exp[-j2πRj(ta)/λ]·

sinc{πB[tr-(R0+Rj0+Rjt)/c]}

(9)

式中： B为信号带宽；sinc(·)为辛克函数。由式(9)可知：干扰信号回波经过距离向压缩后，其主峰出现的时刻为tr=(R0+Rj0+Rjt)/c，与同一时刻发射的信号回波相比，干扰信号回波主峰出现的时刻要滞后，这是因为干扰信号回波的传播路径要比信号回波的传播路径大(R0+Rj0+Rjt>2R0)，因而在距离向压缩成像表现为干扰信号回波产生的“虚假”距离比SAR到目标的实际距离将会变大，其距离偏移量约为

ΔR=(Rj0+Rjt-R0)/2

(10)

另外，将距离函数Rj(ta)曲线在ta=0处展开成两阶泰勒级数

Rj(ta)≈R0+Rj0+Rjt-λfDcj·ta-

(11)

上式的线性部分是距离游走，平方项是距离弯曲，总的变化量即为距离徙步，考虑在一个合成孔径长度内，其可能产生的最大距离徙步约为

(12)

一般情况下，ΔR′≪ΔR，因而距离徙步产生的影响比起干扰信号回波产生的“虚假”距离的干扰效果而言，基本上可以不加以考虑。

3.2 方位向干扰效果分析

对于式(9)，在Fresnel近似下，回波信号在距离向和方位向相互独立，可分离处理[14]，不妨设与ta不相关的脉压输出记为I(tr)=sinc{πB[tr-(R0+Rj0+Rjt)/c]}，与ta相关的方位向信号可分离为

sj(ta)=exp[-j2πRj(ta)/λ]

(13)

(14)

式中“⊗”表示卷积。因在Fresnel近似条件下，SAR的方位向回波数据是线性调频信号形式，且具有较大的时宽带宽积，一般可采用驻定相位定理求取积分[15]，由于散射波干扰方法的本质是改变了信号的传播路径，其方位向干扰信号回波的信号形式仍是线性调频信号，故可采用驻定相位定理求取积分，那么式(14)待积分项的相位为(忽略常数相位)

φ(τ)= 2πfDcjτ+πfRjτ2-

πfR(ta-τ)2

(15)

上式对τ求导，得到驻相点处的关系式[16]

φ′(τ)|τ=τ*=2π(fDcj+fRjτ-fRτ+fRta)

=0

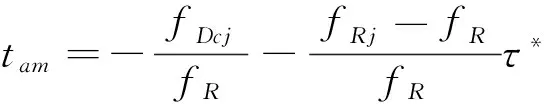
(16)

式中，tam为取驻相点时的方位向时刻，从求得的驻相点τ*，可求得积分I(ta)为[16]

(17)

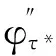
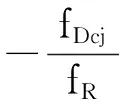
(18)

结合式(18)和图1可知，虚假目标与真实目标T的相对位置，取决于Δx的正负，以SAR飞行方向为正向参考方向，若Δx>0，则虚假目标在目标T的“前方”，反之亦然。

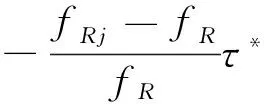
(19)

由式(19)可知，目标方位像的展宽量绝对值大小取决于散射波干扰因子α的大小，其展宽量绝对值越大，导致方位压缩效果越不理想，甚至散焦。在多普勒频带边缘，若多普勒调频率fR失配可以忽略，则因多普勒调频率fR失配而引起的相位误差被限制为[13]

(20)

式中，TL为合成孔径时间，把式(7)代入式(20)中，则限制条件变为

(21)

式中，θH为水平波束宽度。事实上，把式(21)代入式(19)，得

(22)

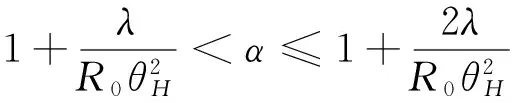
4. 仿真实验

4.1 散射波干扰因子对SAR目标方位像特性的影响

仿真参数的设置如表1所示。

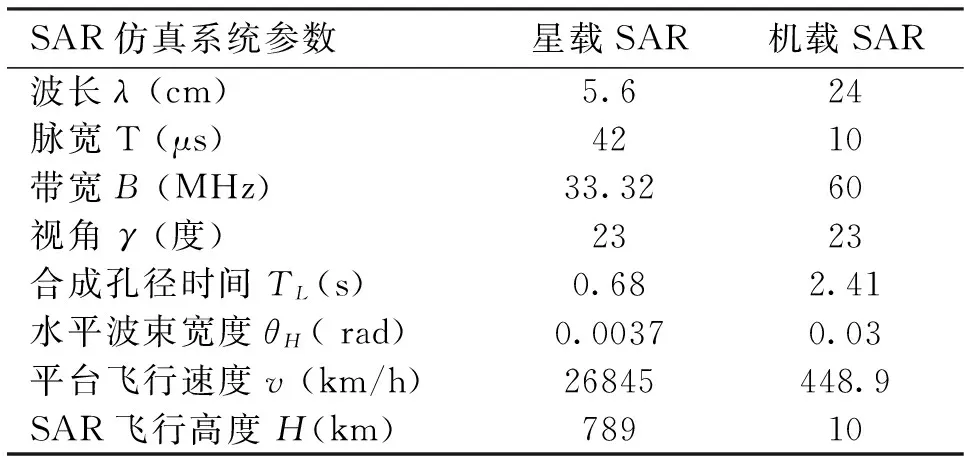
表1 SAR仿真系统参数表

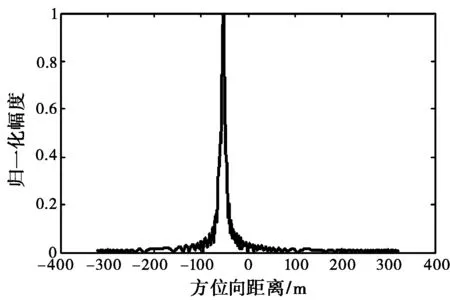
(a) 散射波干扰因子α=1.089

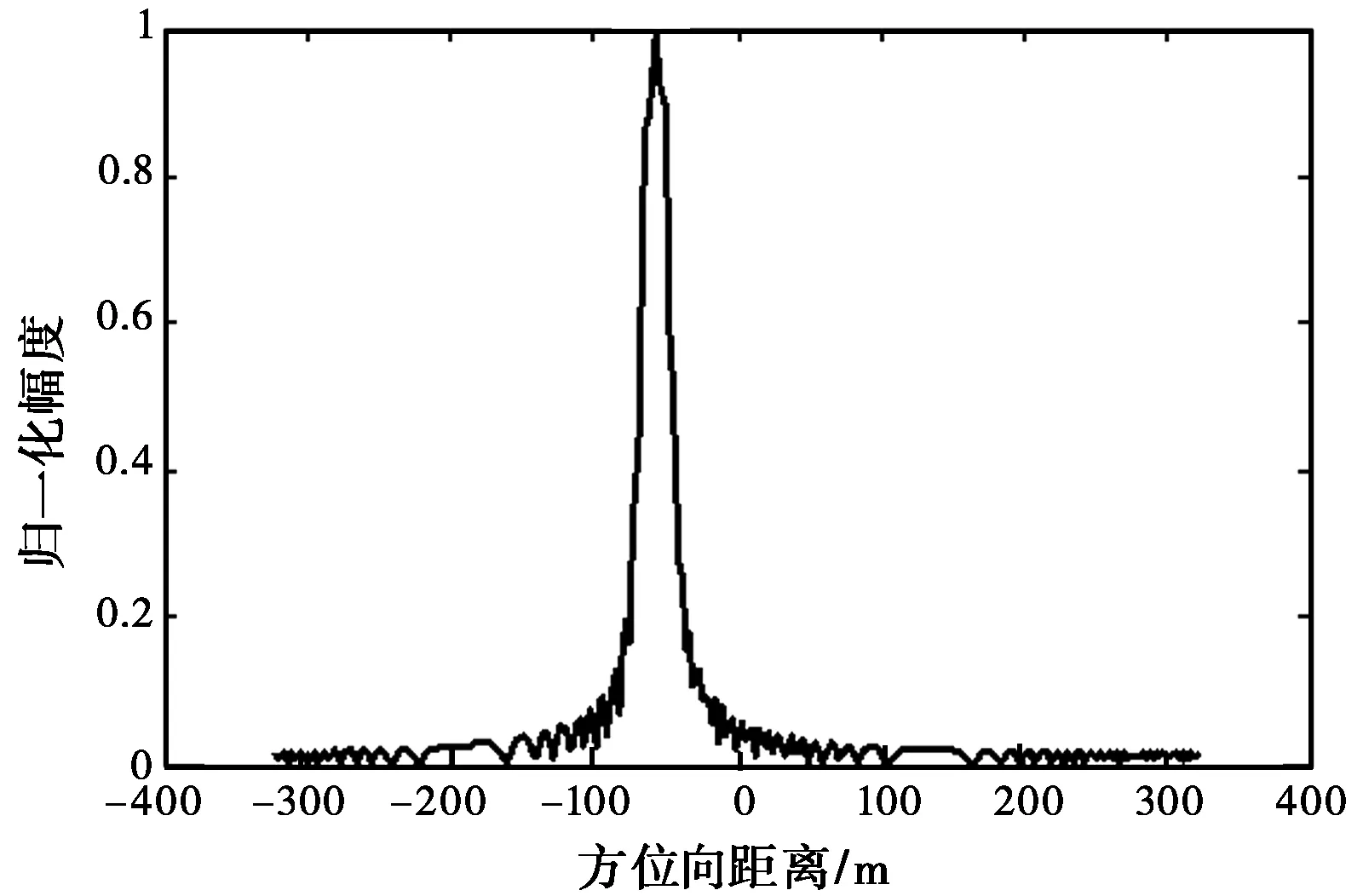
(b) 散射波干扰因子α=1.2

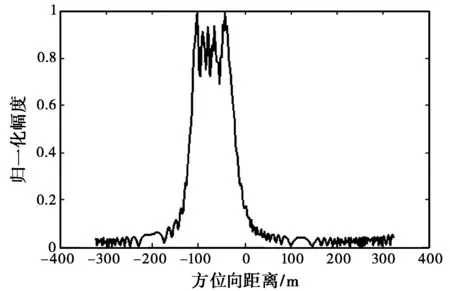
(c) 散射波干扰因子α=2

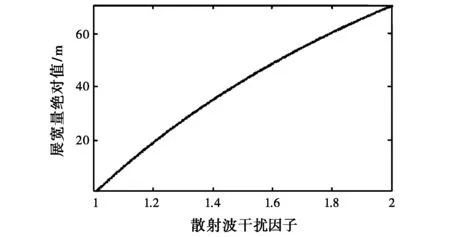
(d) 散射波干扰因子对展宽量绝对值的影响图2 散射波干扰因子对SAR在方位向上压缩成像的影响

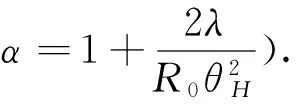
4.2 验证干扰条件仿真实验

仿真时干扰机平台位置的坐标为(-100，4245，h)m，h分别为245 m和3800 m.在机载SAR和星载SAR成像场景中各取五个点目标，其具体的坐标位置如表2所示(单位为m)。

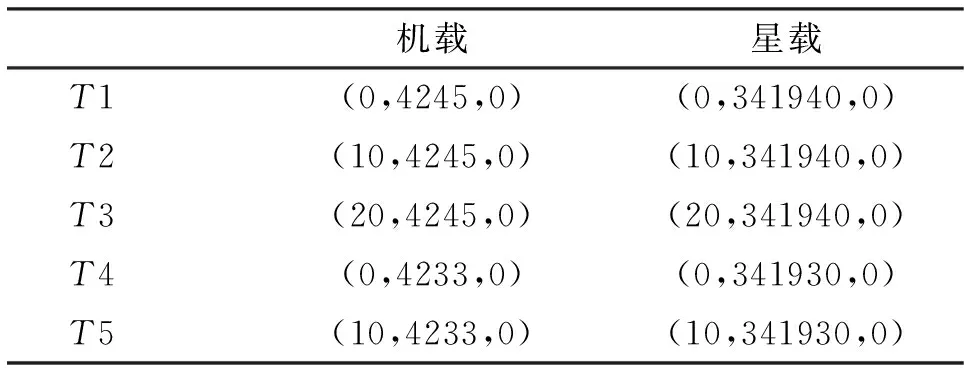
表2 成像目标的坐标位置

采用经典距离-多普勒(R-D)成像算法，其机载和星载SAR的成像结果如图3(看414页)(a)和(b)所示。为了验证散射波干扰方法对机载和星载SAR的不同干扰效果所需的干扰条件，设置如下场景条件：第一次干扰时，干扰机高度h=245 m(这时机载SAR的位置刚好满足式(21))，其仿真结果如图3(c)和(d)所示，这时机载和星载SAR都能满足式(21)，因而干扰效果都为虚假图像欺骗干扰；第二次干扰时，干扰机高度h=3800 m(这时星载SAR刚好满足式(21))，其仿真结果如图3(e)和(f)所示，由于机载SAR已远超出式(21)的限制条件，其干扰效果为散焦图像压制干扰，而星载SAR能够满足上述条件，故干扰效果仍然是虚假图像欺骗干扰。

5. 结 论

在SAR采用经典R-D成像算法基础上，研究了散射波干扰方法对SAR的干扰效果；分析了散射波干扰方法对SAR距离向的干扰效果，理论上推导了其距离偏移量的表达式；利用驻定相位原理，深入地研究了散射波干扰因子对SAR目标方位像的方位偏移量和展宽量绝对值的影响；进而给出了散射波干扰方法对SAR形成各种干扰效果所需的干扰条件，并给出了相关的仿真实验，仿真结果验证了理论分析的正确性。综合来看，散射波干扰方法具有干扰功率利用率高、对侦察参数依赖性低等诸多优点，是一种有效的干扰方法。

[1] 张 云，姜义成，李宏博.一种改善SAR对舰船目标成像质量的新方法研究[J].电波科学学报,2009,24(4)：588-592.

ZHANG Yun，JIANG Yicheng.LI Hongbo. Improving synthetic aperture radar imaging of ship targets[J].CHINESE JOURNAL OF RADIO SCIENCE,2009,24(4)：588-592.(in Chinese)

[2] 甘荣兵，王建国. 对SAR的几何目标欺骗干扰的快速算法[J].现代雷达,2006,28(2):40-42.

GAN Rongbin，WANG Jianguo. Fast generation algorithm of geometric target deceive jamming signal to SAR[J].Modern Radar,2006,28(2):40-42.(in Chinese)

[3] 白雪茹，孙光才，周 峰，等.基于旋转角反射器的ISAR干扰新方法[J].电波科学学报,2008,23(5)：865-872.

BAI Xueru，SUN Guangcai，ZHOU Feng, et al. A novel ISAR jamming method based on rotating angular reflectors [J].CHINESE JOURNAL OF RADIO SCIENCE, 2008,23(5)：865-872.(in Chinese)

[4] 胡东辉,吴一戎.合成孔径雷达散射波干扰研究[J].电子学报,2002,30(12):1882-1884.

HU Donghui，WU Yirong. The Scatter Wave Jamming to SAR[J].ACTA ELECTRONICA SINICA,2002, 30(12): 1882-1884.(in Chinese)

[5] 高晓平,雷武虎.SAR散射波干扰实现方法的研究[J].现代雷达,2006,28(8):22-24.

GAO Xiaoping，LEI WUhu. Method of Implementing Scatter Wave Jamming[J]. Modern Radar,2006,28(8): 40-42.(in Chinese)

[6] 唐 波.合成孔径雷达的电子战研究[D].北京:中国科学院电子学研究所, 2005.

[7] LI Tao，CHEN Weidong. A sudy on Scatter Wave Jamming for Countering SAR,2007 5th Inernational Conference on Microwave and Millimeter Wave Technology proceeding[C]. Guilin, 2007.

[8] 尹志盈，杜 鹏，朱秀芹.SAR散射波干扰研究[J].电波科学学报,2007,9(22):481-484.

YI Zhiying，DU Peng，ZHU Xiuqin. Study Scatter Wave Jamming on SAR[J].CHINESS JOURNAL OF RADIO SCIENCE,2007,9(22)：481-484.(in Chinese)

[9] 田贤峰,方广有.星载SAR散射波欺骗干扰研究[J].微计算机信息,2009,25(10):254-255.

TIAN Xianfeng，FANG Guangyou. Study on Scatter Wave Deceptive Jamming to Spaceborne SAR[J]. NTROL & AUTOMATION,2009,25(10)：254-255.(in Chinese)

[10] WANG Wenqin, CAI Jingye. A technique for jamming Bi- and multistatic SAR systems [J]. IEEE Geoscience and remote sensing letters, 2007, 4(1): 80-82.

[11] 张 瑛,王建国.双基地合成孔径雷达弹射式干扰研究[J].电子与信息学报,2007,29(5)：1061-1064.

ZHANG Ying,WANG Jianguo.Research on rebound jamming against BiSAR[J]. Journal of Electronics & Information Technology,2007,29(5)：1061-1064. (in Chinese)

[12] 孙云辉,陈永光,焦 逊.星载SAR应答式欺骗干扰研究[J].电子对抗技术,2004,19(2):23-26.

SUN Yunhui, CHEN Yongguang, JIAO Xun .On Study of the Responsive Deception for Spaceborne SAR[J]. Electronic Information Warfare Technology, 2004,19(2):23-26. (in Chinese)

[13] CURLANDER J C，ROBERT N M. 合成孔径雷达-系统与信号处理[M].韩传钊,译.北京：电子工业出版社,2006：104-143.

[14] CUMMING L G.，WONG F H.合成孔径雷达成像：算法与实现[M].洪文，胡东辉，等译.北京：电子工业出版社 2007：34-86.

[15] 张澄波.综合孔径雷达原理系统分析与应用[M]. 北京:科学出版社,1989：50-98.

[16] 李家春.周显初.数学物理中的渐近方法[M].北京:科学出版社,1998:103-150.