一种多通道SAR地面快速目标高概率检测方法

钱 江 孙光才 李凉海 邢孟道

(1.西安电子科技大学雷达信号处理国家重点实验室，陕西 西安 710071； 2.中国航天科技集团第七〇四研究所，北京 100076)

1.引 言

合成孔径雷达地面动目标检测已广泛应用于军事侦察和交通监视等领域，典型的应用实例为美国采用联合监视目标攻击雷达系统(JSTARS)的GMTI模式在海湾战争中侦察到伊拉克从科威特撤军的画面。现在SAR-GMTI已经开始应用在星载雷达上，比如加拿大的Radarsat-II上的运动目标检测实验(MODEX)模式[1]，还有德国的TerraSAR-X系统[2]，都已经逐渐开始SAR-GMTI实验。目前国内许多科研院所也已经进行了许多理论研究和外场试验[3-4]。

常规三通道SAR-GMTI在SAR图像域采用天线相位中心偏置(DPCA)技术进行通道间两两杂波对消，再利用第三个通道信息取干涉相位，得到运动目标参数。但是对于存在PRF模糊的快速目标而言，这种方法是有局限性的，它受制于脉冲重复频率。目标的径向速度会引起方位多普勒偏移，由于方位上Nyquist采样特性使得方位多普勒谱存在模糊，对于速度引起的多普勒偏移超过PRF/2的情况，通过估计运动目标多普勒中心是无法获取其运动参数的。我们考虑到径向速度引起的距离走动不受方位采样影响，因此可以通过考察距离走动信息来完成解PRF模糊和速度估计。

本文首先对基带多普勒偏移对应的速度分量引起的走动采用Keystone变换[5-6]进行校正，对PRF整数倍多普勒偏移对应速度引起的确定的离散走动量则可在时域加以校正。校正后再进行方位匹配滤波得到运动目标SAR图像。这里根据Keystone变换后直线走动率与模糊数的线性关系，按照有限的模糊数进行距离走动校正，当前具有相同模糊数的目标都被校平，再进行恒虚警(CFAR)检测[7]和参数提取并实现定位。同时在文中分析了距离走动对方位匹配滤波的影响，并且考虑了快速目标引起的PRF模糊和相位模糊问题。

2.多通道SAR-GMTI快速目标检测理论及算法

2.1 多通道SAR-GMTI信号模型

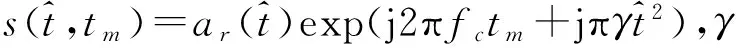
图1 SAR-GMTI天线与动目标的几何关系

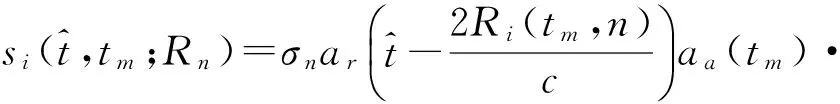
(1)

距离脉压后补偿前后通道间距引起的方位包络平移和相位差异，对消得

(2)

式中：

2.2 动目标距离走动校正

一般地，距离走动校正方法首先是通过Radon或者Hough变换[8]确定目标轨迹的斜率，然后根据斜率构造补偿函数在距离频域进行补偿。但是由于Radon变换与Hough变换都需要设置搜索步长，步长越小估计精度越高，但是搜索时间越长。本文利用Keystone变换后动目标距离走动量与模糊数成正比的特点，设计简单而有效的搜索方法完成距离走动校正。Keystone变换后基带多普勒中心对应的距离走动被消除，剩余由多普勒模糊分量对应的距离走动则通过构造相应的补偿函数进行补偿。

(3)

其随慢时间变化的相位可以表示为

=φ1(fr,tm)+φ2(fr,tm)

(4)

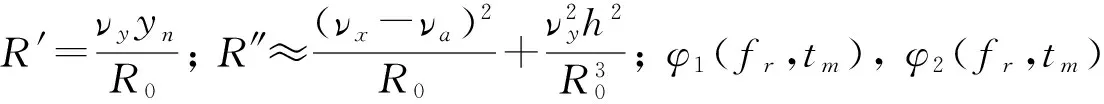
2πM·PRF·tm

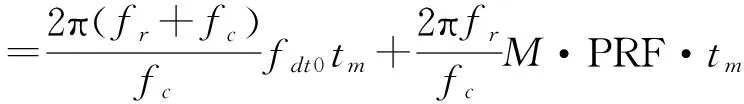
(5)

进行Keystone变换[5]，即令

(6)

则有

(7)

由于fr≪fc，相位(7)可以表示为

(8)

从式(8)可知，Keystone变换之后，由基带多普勒中心对应的走动分量已经被校正，但是多普勒模糊分量对应的走动分量没有被校正。

2.3 动目标速度模糊数的确定

基带多普勒中心对应的速度可以通过Keystone变换加以校正，而且对于所有目标其基带多普勒对应的距离走动都被校正，但是式(8)中每个目标的模糊多普勒分量对应的距离走动是不一样的，需要逐个加以校正，一种方法是在距离压缩域通过Radon变换等检测直线的方法确定直线斜率进而确定多普勒模糊数，这种方法计算量比较大。本文根据模糊数与直线斜率的关系，通过稀疏Radon变换实现高效搜索，即利用Keystone变换后动目标轨迹与整数倍PRF对应的多普勒偏移的线性关系，构造有限个距离走动函数进行校正，并对信号进行方位上的幅度求和，最大值对应的模糊数就是动目标的模糊数。但是这是对距离包络幅度值进行积累的，噪声也得到积累，它仅对信噪比较高的情形适用。为了减轻噪声的影响，可先对信号进行方位匹配滤波，然后CFAR检测，并将其加窗提取出来变换到距离压缩方位时域，进行稀疏Radon变换确定动目标模糊数，这样达到最大限度地减少噪声的影响。

2.4 方位匹配滤波

如果目标的距离走动量刚好被走动补偿函数补偿，那么方位匹配滤波后将得到充分的相干积累，否则引起散焦。

假如已知目标的模糊数为M，构造补偿函数为

(9)

将式(9)与式(3)相乘进行距离走动补偿并距离向逆傅里叶变换(IFFT)，忽略常数项，得到信号为

aa(τm)exp(j2πfdt0τm)·

(10)

可见由模糊多普勒分量对应的速度引起的距离走动项已经被校平。

(11)

用杂波的匹配函数对信号进行方位向匹配滤波，匹配函数为

(12)

(13)

2.5 距离走动对动目标成像的影响分析

如果用任意模糊数N进行距离走动补偿，补偿函数为

(14)

一次相位项φ1(fr,τm)补偿后得到

PRF·τmfr/fc

(15)

距离IFFT后，进行方位傅里叶变换(FFT)得到

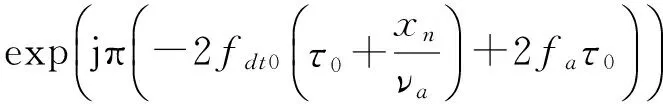
(16)

与方位匹配函数sM相乘并作IFFT得，

(17)

式中：

AΔf为方位上的窗函数，窗宽为Δf/ka0.可见此时方位和距离都是散焦的，方位中心位置由距离走动量、动目标多普勒中心、多普勒调频率和杂波多普勒调频率共同决定，但是动目标调频率参数是无法确定的，也即无法准确定位。而如果已经补偿动目标的距离走动，那么方位位置只与动目标多普勒中心和杂波多普勒调频率有关，而这些参数都是可以确定的，所以是可以实现定位的。

2.6 动目标测速与定位

(18)

同理

(19)

于是可得干涉相位为

φ=angle(C12·conj(C32))

(20)

φ0+2πn,n=0,±1,±2，…,其中φ0为模糊相位。下一节将分析速度引起的两种模糊问题并讨论相应的解模糊方法。

2.7 由速度产生的两种模糊分析

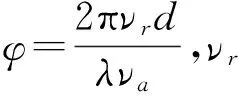
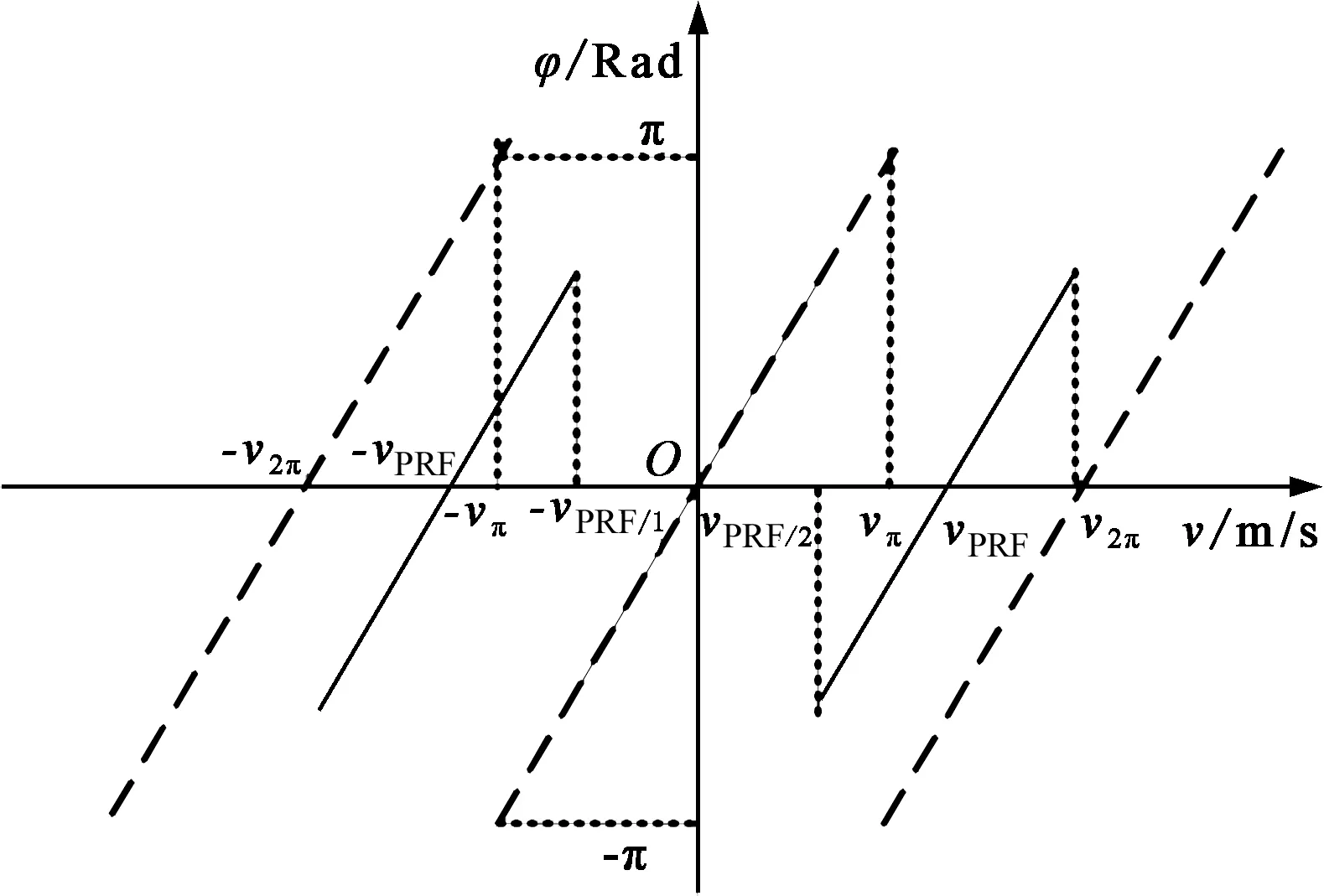
(a) νPRF<ν2π，只有PRF模糊

(b) νPRF≥ν2π，两种模糊同时存在图2 速度与干涉相位的关系

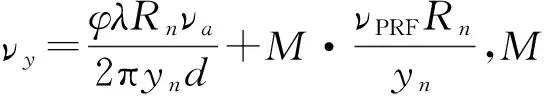
第二种情况如图2(b)，νPRF≥ν2π，存在两重模糊，速度存在相位模糊的区间为(νπ+kνPRF，νPRF-

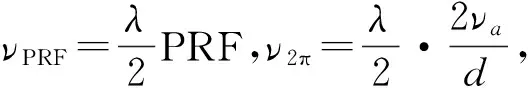
获得动目标的速度估计νy后就可以进行定位，运动目标径向速度会引起方位偏移，偏移量为

(21)

2.8 性能分析

传统SAR-GMTI方法不进行走动校正直接方位匹配滤波，这会导致动目标在SAR图像上的散焦，本文对快速目标走动校正后进行匹配滤波，然后在图像域进行CFAR检测，可以提高动目标检测概率。

这里对本文方法的检测性能通过蒙特卡罗试验进行评价，在不同信噪比条件下，比较本文方法与传统SAR-GMTI方法对快速目标的检测概率。本文根据文献[12]定义SNR为动目标聚焦后峰值点功率与噪声功率之比。从图3可见，同样检测概率下，本文方法所需的信噪比可以比常规方法低大致2 dB.文献[13]中一次检测是在距离脉压域进行的，必须检测并提取动目标的轨迹，然后校正距离走动，并方位脉压得到动目标的像，再进行二次检测。所以该方法实际上大大取决于距离脉压后信号的SNR。与文献[13]不同的是，这里并未采用基于距离脉压域的直线检测方法，而是在距离走动校正后进行方位匹配滤波，这样最大程度上实现动目标能量的相干积累。

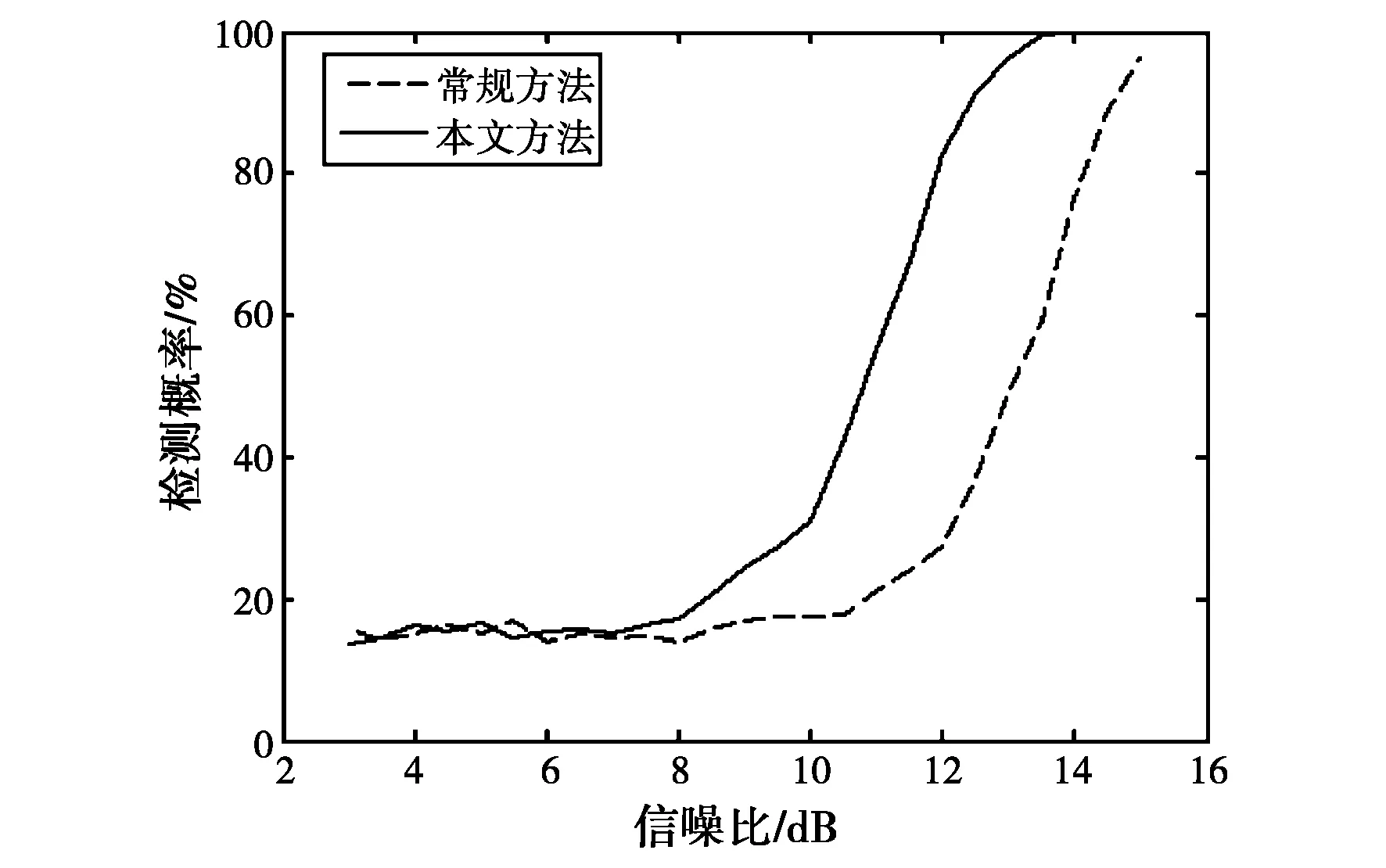
图3 不同信噪比条件下两种方法检测概率的比较

3.实测数据处理及结果分析

本节采用实测数据对本文的方法进行验证。该数据为某所录取的分辨率为12 m×12 m的机载条带三通道SAR-GMTI数据，载机高度6 km，场景斜距60 km.雷达工作在X波段，采用全孔径发射三天线同时接受的模式。选取某段高速公路场景回波作为实验数据。

图4(a)为原始数据距离脉压后目标T2的直线轨迹，对距离脉压结果进行Keystone变换后得到的结果见图4(b)，可见直线斜率有微小的变化，也就是基带多普勒中心引起的距离走动被校正。在式(9)设置模糊数为-1进行距离走动校正时T2的走动被校平，结果如图4(c)。图4(d)为方位匹配滤波后T2的粗聚焦结果。图4(e)为用模糊数0构造距离走动校正函数时检测结果， 常规SAR-GMTI处理可以视为采用本文方法中模糊数为0的特殊情况。白色“×”为检测到的目标，对于目标散焦的情况，会检测到多个散射点，需要根据各散射点距离远近进行聚类，然后以聚类中心作为检测到的目标，再将该类的散射点求干涉相位平均获取目标速度信息。图中标注的“□”表示采取其它模糊数校正走动后被检测到而在0模糊数时未被检测到的目标，这也即该方法与常规SAR-GMTI方法相比的优势所在，对常规方法得到的SAR图像进行CFAR检测会使存在距离走动且散焦的弱目标产生漏警。

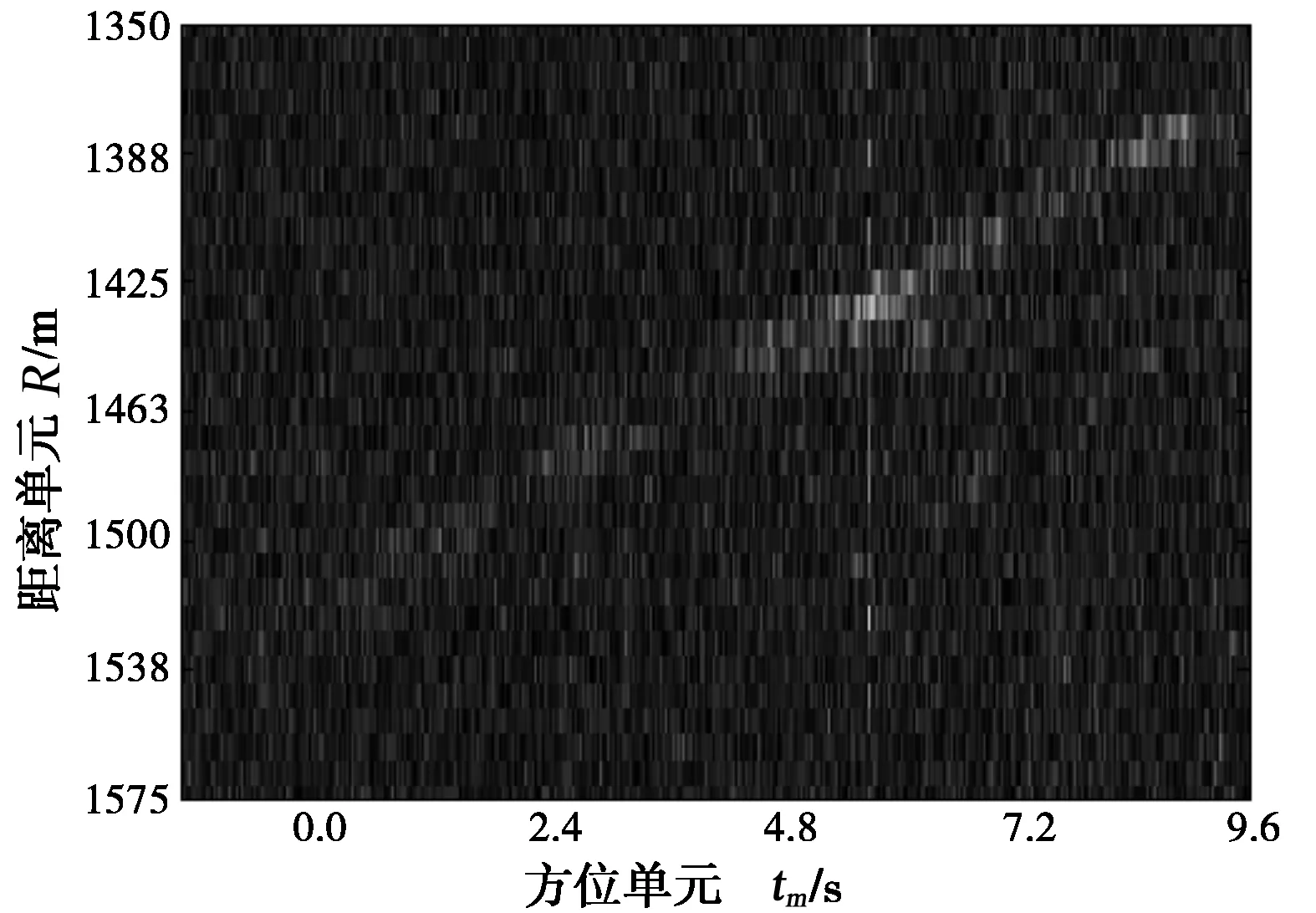
(a) 距离脉压后T2的轨迹

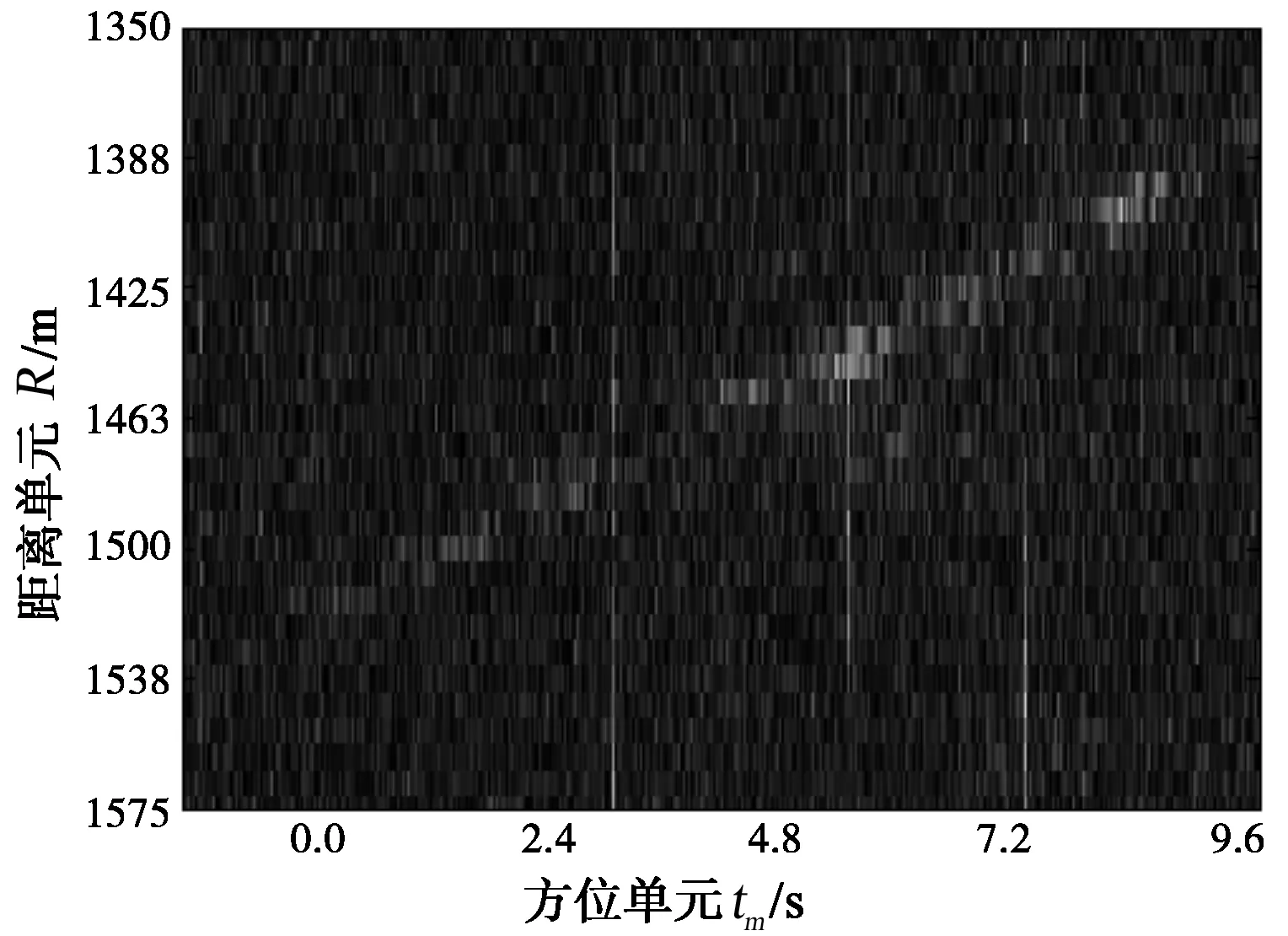
(b) Keystone变换后T2的轨迹

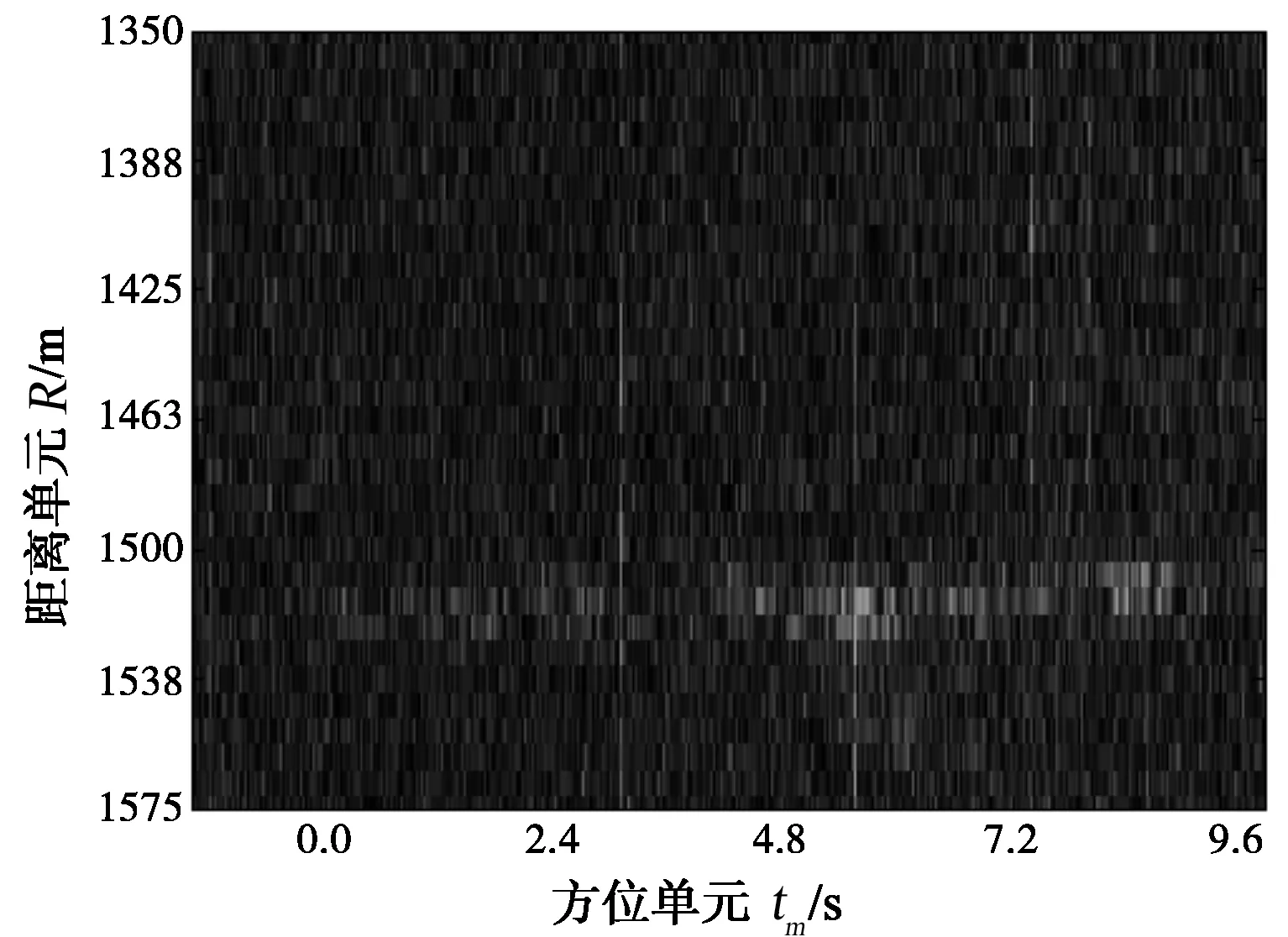
(c)设置模糊数为-1进行距离走动校正

(d) 方位匹配滤波

(e) 模糊数为0的检测结果

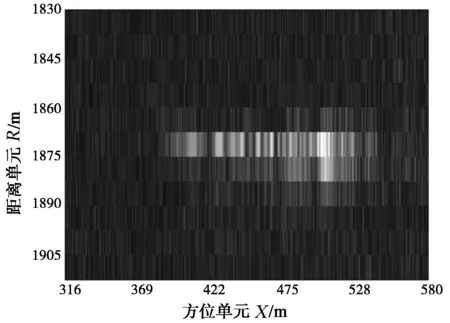
(f) 目标T4所在单元为中心的数据块

(g) 将其变换到方位原始数据域

(h) 用不同模糊数对应的距离走动量进行校正

(i) 动目标定位结果图4 实测数据动目标检测定位

由于同一个目标可能在不同模糊数校正距离走动后的图像中出现，这就需要确定该目标的模糊数，如果被检测到目标的模糊数为M，而当前校正距离走动的模糊数为N(N≠M)，那么就不进行后续测速定位操作。图4(f)～(h)给出目标T4模糊数确定过程，在图4(e)中选择T4为中心11×2001的数据块进行操作，可见该目标的模糊数为0，将该数据块变换到方位原始数据域，再构造不同模糊数对应的距离走动校正函数校正走动，根据系统参数可得模糊数区间为[-3，3]，图4(h)给出不同模糊数的走动校正过程，如果目标的模糊数为当前走动校正函数对应的模糊数，那么目标距离走动就被校平，同时也得到了该目标的模糊数。我们注意到当目标走动被校平时，直线幅值进行累加得到的值比存在距离走动时大，这样就可以以各距离单元幅值累积值最大作为准则确定走动是否被校正。最终动目标定位结果见图4(i)，白色圆圈代表检测到的目标，白色正方形代表定位后的目标。通过本方法得到的目标运动参数见表1。

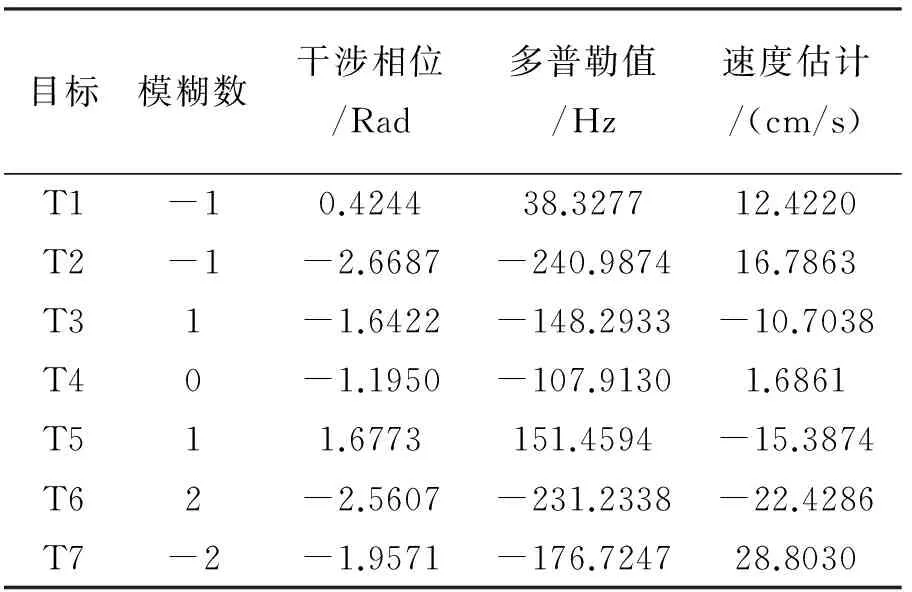
表1 动目标运动参数

4.结 论

本文讨论了SAR-GMTI快速目标检测问题。本文对于基带多普勒偏移对应的速度分量引起的走动采用Keystone变换进行校正，对PRF整数倍多普勒偏移对应速度引起的确定走动量在时域加以校正。对比传统SAR成像后对消再检测的方法，该方法能够在最大程度上检测到微弱目标。文中分析了距离走动对方位匹配滤波的影响，说明传统方法引起弱目标漏检的原因,并且考虑了快速目标引起的PRF模糊和相位模糊的关系，对系统参数设计具有一定的指导意义。如何实现高效性的方位聚焦，以进行更好的相干积累，这将是我们下一步将要进行的工作。

[1] LIVINGSTONE C E and THOMPSON A A. The moving object detection experiment on RADARSAT-2[J]. Canadian Journal of Remote Sensing, 2004, 20(3): 355-368.

[2] MEYER F, HINZ S, LAIKA A, et al. Performance analysis of the terraSAR-X traffic monitoring concept[J]. ISPRS Journal of Photogrammetry & Remote Sensing, 2006, 61(34): 225-242.

[3] 宁 蔚, 廖桂生. 机载双通道雷达空时自适应处理中的样本去污[J]. 电波科学学报,2007, 22(3): 470-475.

NING Wei, LIAO Guisheng. Elimination of pollutions in training samples for airborne dual-channel radar′s space-time adaptive processing[J]. Chinese Journal of Radio Science, 2007, 22(3): 470-475. (in Chinese)

[4] 王宏远, 危 嵩, 孙 文. DBS高分辨成像及动目标轨迹处理[J]. 电波科学学报,2005,19(5): 637-641.

WANG Hongyuan, WEI Song, SUN Wen. High resolution DBS imaging and moving target trajectory processing[J]. Chinese Journal of Radio Science, 2005,19(5): 637-641. (in Chinese)

[5] PERRY R P, DIPIETRO R C, and FANTE R L. SAR imaging of moving targets[J]. IEEE Trans. Aerosp. Electron. Syst., 1999, 35(1): 188-200.

[6] 陈文驰,刘 飞. 一种低信噪比下的ISAR 成像实现方法[J]. 电波科学学报, 2010, 25(3): 587-589.

CHEN Wenchi, LIU Fei. An implementation method of ISAR imaging at the low SNR level [J]. Chinese Journal of Radio Science, 2010, 25(3): 587-589. (in Chinese)

[7] 胡文琳, 王首勇, 王永良, 等. 多分布类型杂波背景下恒虚警处理器性能分析[J]. 系统工程与电子技术, 2007, 29(6): 883-886.

HU Wenlin, WANG Shouyong, WANG Yongliang, et al. Performance analysis of CFAR processor in multi-distribution clutter background[J]. Systems Engineering and Electronics, 2007, 29(6): 883-886. (in Chinese)

[8] ZHANG Q, YEO T S, TAN H S, et al. Imaging of a moving target with rotating parts based on the hough transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291-299.

[9] 吕孝雷，邢孟道，潘月娥，等. 基于联合像素干涉统计特性的三通道动目标检测方法[J]. 电子学报, 2008, 36(12): 2319-2323.

LV Xiaolei, XING Mengdao, PAN Yuee, et al. Detection of three-channel ground moving targets using statistical properties of joint pixel paris interferograms[J]. Acta Electronica Sinica, 2008, 36(12): 2319-2323. (in Chinese)

[10] XIA Xianggen and WANG Genyuan. Phase unwrapping and a robust chinese remainder theorem[J]. IEEE Signal Processing Letters, 2007, 14(4): 247-250.

[11] LI Gang, XU Jia, PENG Yingning, et al. An efficient implementation of a robust phase-unwrapping algorithm[J]. IEEE Signal Processing Letters, 2007, 14(6): 393-396.

[12] LIU Baochang, WANG Tong, BAO Zheng. Slant-range velocity estimation based on small-FM-rate chirp[J]. Signal Processing, 2008, 88(10): 2472-2482.

[13] 吕孝雷, 齐飞林, 邢孟道, 等. 三通道SAR-GMTI地面快速目标检测[J]. 系统工程与电子技术, 2009, 31(7): 15811587.

LV Xiaolei, QI Feilin, XING Mengdao, et al. Ground fast moving target detection based on tri-channel SAR-GMTI[J]. System Engineering and Electronics, 2009, 31(7): 1581-1587. (in Chinese)