基于基尔霍夫驻留相位近似法的深粗糙度高斯型粗糙面光散射

田 炜,任新成

(延安大学 物理与电子信息学院,陕西 延安 716000)

0 引言

近几十年来,粗糙面散射一直是一个活跃、有大量实际应用,且为多学科领域共同研究的热点,如海面通信会受粗糙面散射的影响;无线电海洋学中,根据雷达接收的散射波识别海上或海面附近的目标;红外、可见光遥感中,利用目标对光波的散射取得数据以识别目标形态和特征[1～6]。另外,有关粗糙面散射理论在跟踪制导、水下声学、雷达目标成像、隐身、固体物理、辐射测量学和天文学等领域均有广泛的应用。

目前,微粗糙表面的散射理论已日趋成熟,但深粗糙度表面散射尚待进一步研究,尤其是后向散射增强效应也越来越引起关注[7～12]。本文根据光的电磁场理论推导了基尔霍夫驻留相位近似法相关公式,用基尔霍夫驻留相位法研究了深粗糙度高斯型粗糙面的光散射[7、8]。

1 基尔霍夫驻留相位近似法理论

粗糙面散射几何关系如图1所示。图中：ki,ks分别为入射波和反射波的波矢;θi,θs分别为入射角和散射角;φs为散射波的方位角。当光波由上向下照射到两个半无限介质的分界面时,入射能量部分形成散射,部分透射进入下层介质。在两种均匀介质平面的交界面上,平面波的反射与透射能精确解出。但当交界面不规则时,就不存在精确闭合解。仅当交界面上散射单元远小于或远大于射波波长时,才有近似解[13]。

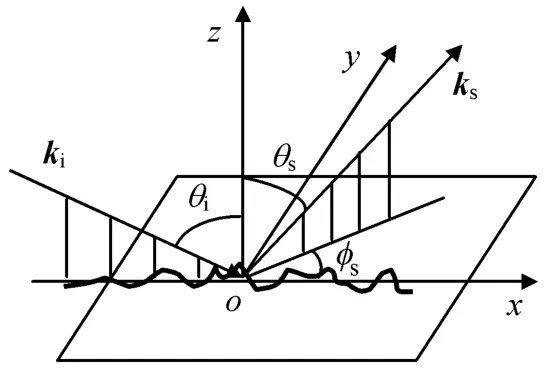
图1 粗糙面散射几何关系Fig.1 Geometry of optical wavescattering from Gaussian rough surface

1.1 介质中的散射场

封闭面为边界的无源区内任一点的散射场可用表面相切的场表示,有

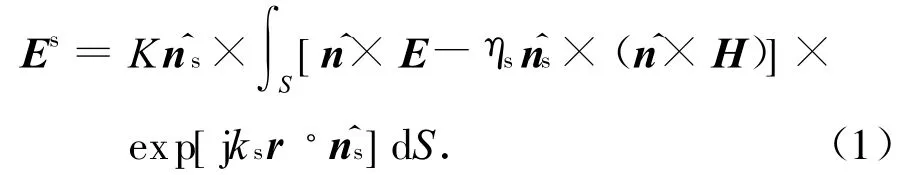
取本地基准坐标系时界面的切向场更易求得,如图2所示。图中：分别为入射和反射方向的单位矢量。介质1的总切向电磁场

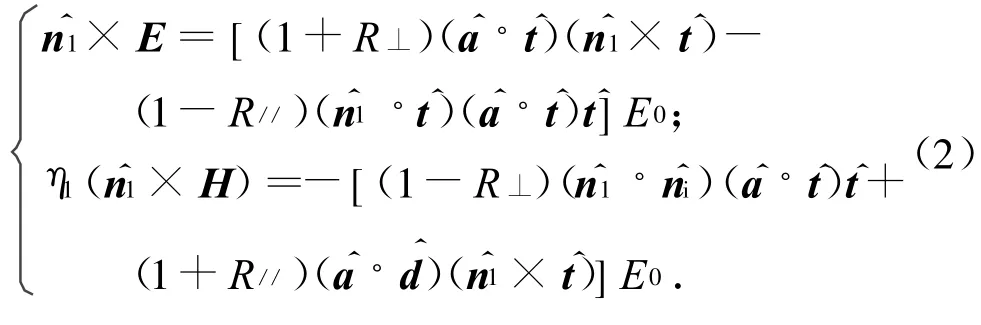
式中：E0为入射波电场强度幅值;为介质1中的界面单位法向矢量;R⊥,R//分别为水平和垂直极化的菲涅尔反射系数;为单位极化矢量;η1为介质1的本质阻抗;。

将式(2)代入式(1),得介质1中的散射场

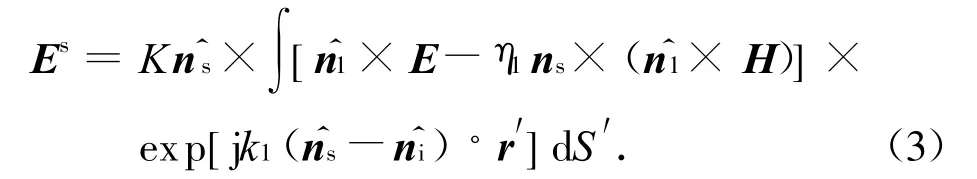
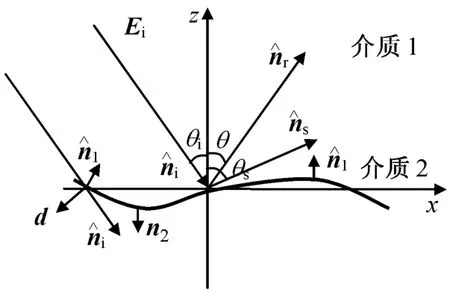
图2 本地基准坐标系Fig.2 Local standard coordinates

基尔霍夫驻留相位法只能沿在表面上存在镜面点的方向发生散射,故此处排除了绕射效应。由式(3)的相位因子Q得近似关系式,即

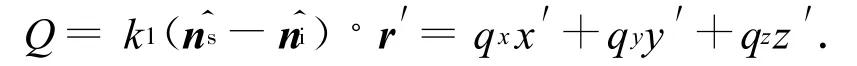
式中：

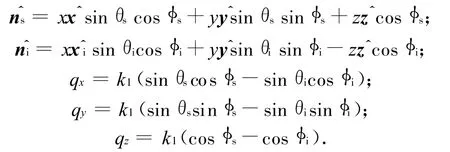
此处：φi为入射波的方位角。

若某点的变化率为零,则该点的Q被认为是稳态的,即

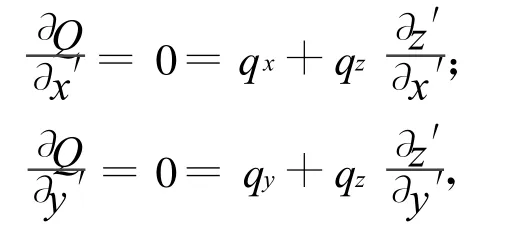
因此,表面斜度的偏导数可用相位分量替代

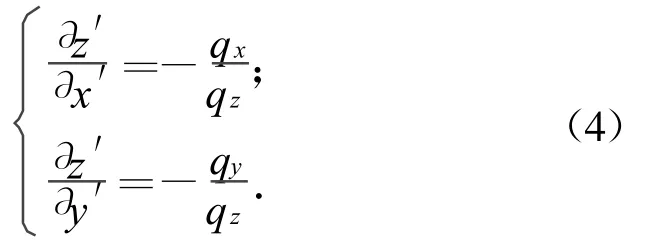
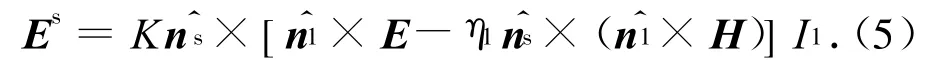
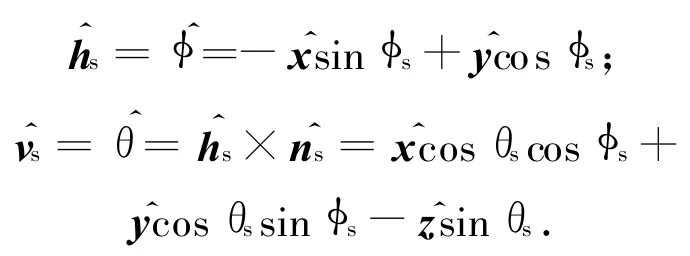
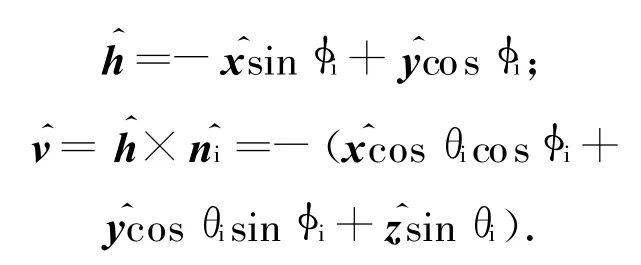
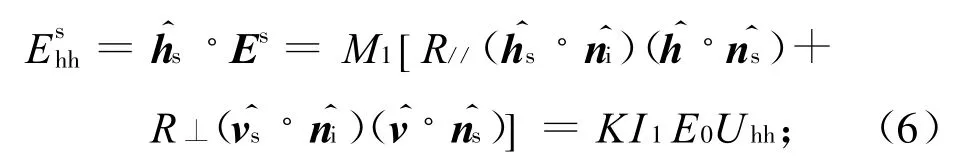
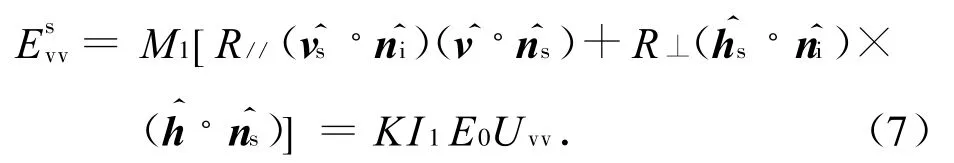
式中：M1=K I1E0q|qz|/{[]×kqz};Uhh,Uvv分别为水平和垂直极化散射场中的极化因子。由式(6)、(7)可导出

a)入射波为水平极化时

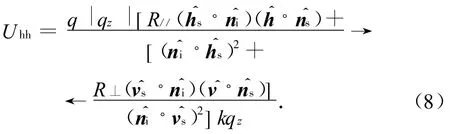
b)入射波为垂直极化时

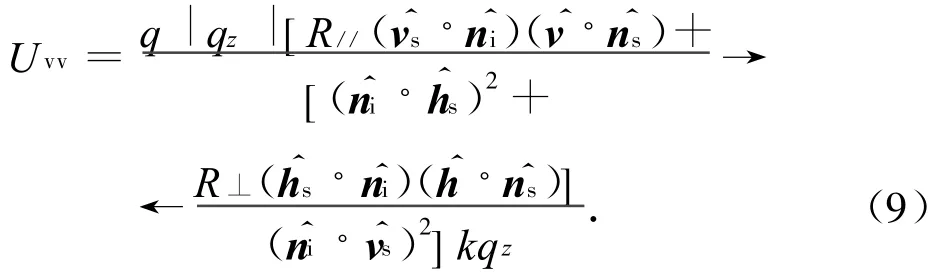
式中：

此处：εr为相对介电常数。

1.2 散射系数

定义在特定方向上扩展目标的散射系数为：该方向上产生相同散射功率密度的各向同性等效散射体的总散射功率与照射面积上总入射功率的比值,即

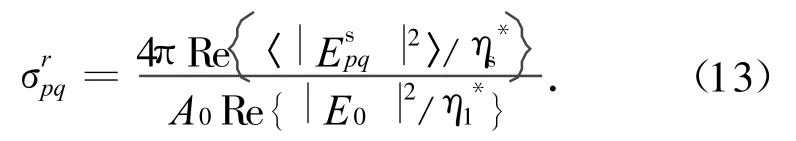
式中：A0为照射面积;〈〉表示集平均;上标*表示复共轭。

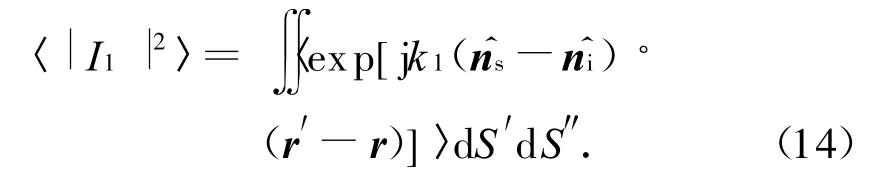
式中：d S′,d S″分别表示在粗糙面上以(x′,y′),(x″,y″)为中心的面元。因

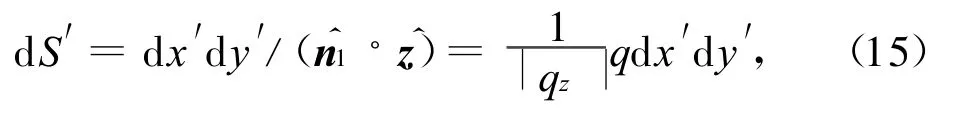
则有

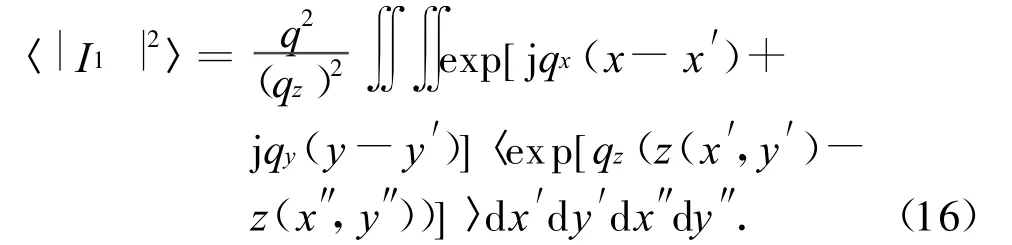
式中的因子〈〉被认为是z(x′,y′),z(x″,y″)的联合特征函数。对高斯型随机过程,特征函数

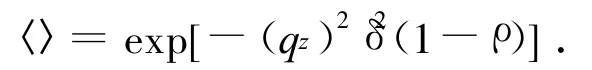
式中：δ为高度起伏均方根;ρ为粗糙面高度起伏相关系数。

平稳过程仅取决于差变量,即u=x′-x″,v=y′-y″。设照射面积为2L×2L,用差变量替代,式(14)演变为

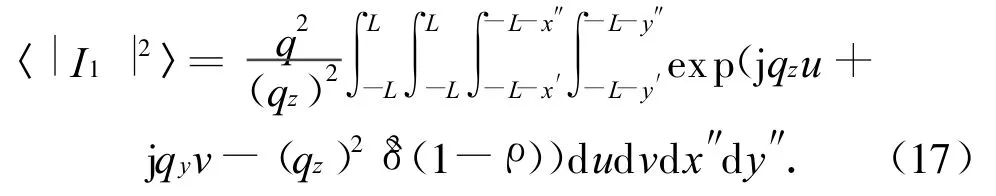
式(17)互换积分次序,可化简关系

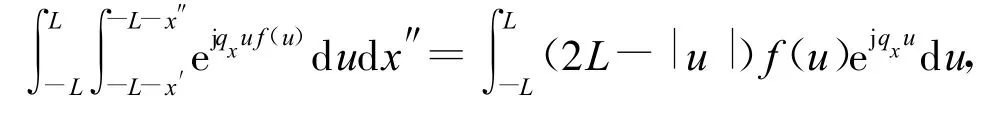
则式(16)可变为

再作进一步的简化则需附加假设条件,常采用的两种假设条件是：表面粗糙度为各向同性;应满足(qz)2δ2＞10,以使u,v均为小量时,再用ρ值在原点附近以泰勒级数展开,取其前2项作为近似值。在这种情况下,将u,v换成极坐标r,φ更方便。与2L相比,可忽略|u|,|v|,然后对φ求积分,式(18)可化为

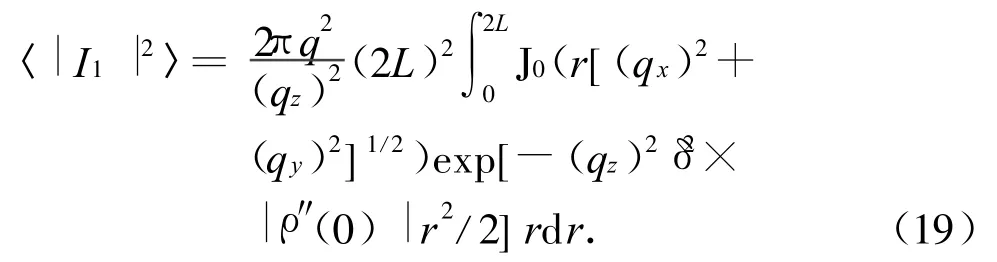
式中：J0为零介贝塞尔函数;ρ″(0)为在原点处ρ的二阶微商;(2L)2为照射面积A0。由于在r为大值时,式(19)的被积函数可忽略不计,因此如将积分上限延伸至无穷,也不会产生明显的误差。积分范围变化后,求得式(16)的积分结果为

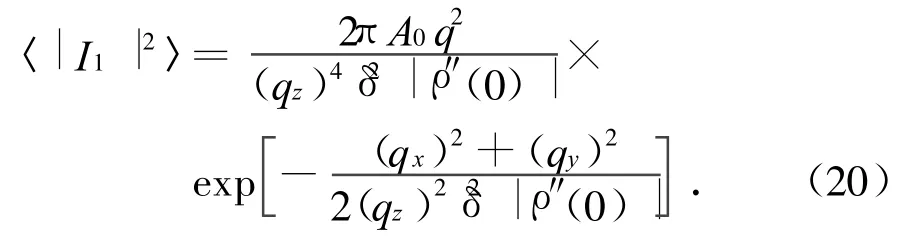
将式(20)代入到介质1散射场表达式的乘积中,得

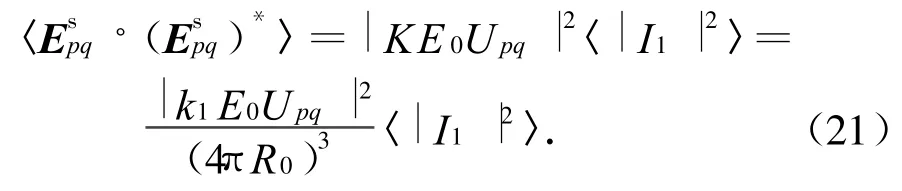
再将式(20)代入式(11)、(12),得在介质1的双基地散射系数

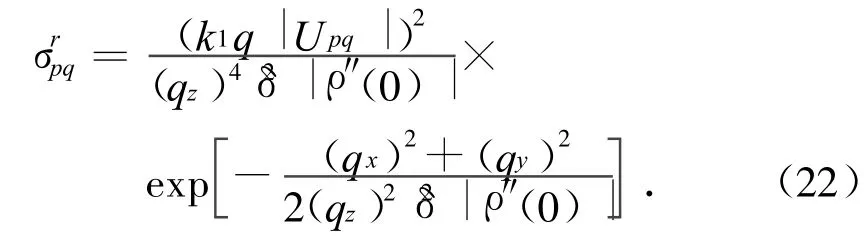
在面散射中,最使人感兴趣的是后向散射,即θi=θs,θs=π。在入射面内,为零。由式(22)可得后向散射系数

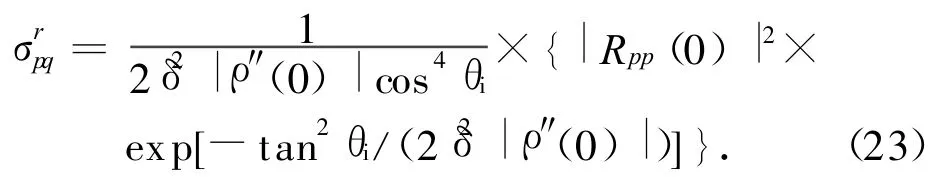
式中：Rpp(0)为法向入射时的菲涅耳反射系数,且

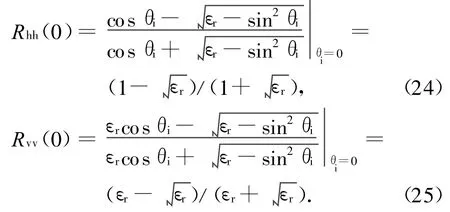
本文采用高斯粗糙面,则粗糙面高度起伏相关系数在原点处的二阶微商

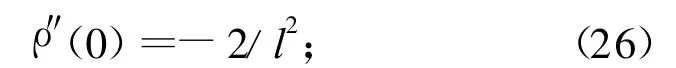
深粗糙度高斯型粗糙面散射系数

由式(8)～(12)、(22)、(26)、(27)可得双站条件下,对任一种极化状态的散射波,在入射波波长、入射角以及散射方位角一定的条件下不同散射角的散射系数,同时受粗糙面高度起伏均方根、相关长度、介质介电常数的影响。当入射角、散射角、散射的方位角、粗糙面高度起伏均方根、相关长度、介电常数一定时,散射系数受入射波波长的影响,可通过数值计算的方法获得这些特征,得到一些普遍、有意义的结论。

由式(23)～(27)可得单站条件下,当入射波波长一定时,不同入射角的散射系数同时受粗糙面高度起伏均方根、相关长度、介电常数的影响。当粗糙面高度起伏均方根、相关程度、介电常数一定时,散射系数受入射波波长的影响,可通过数值计算的方法获得这些特征,得到一些普遍、有意义的结论。

2 数值计算

2.1 双站

2.1.1 粗糙面高度起伏均方根、相关长度、介质介电常数对散射系数的影响

限于篇幅,仅给出HH极化情形。在λ=1.06μm,θi=30°,φs=0°条件下,由式(8)～(12)、(22)、(26)、(27),用数值计算可得不同θs的双站散射系数σ,以及粗糙面粗糙度参数δ与l、介质介电常数ε对σ的影响分别如图3～5所示。图中：k为波数。

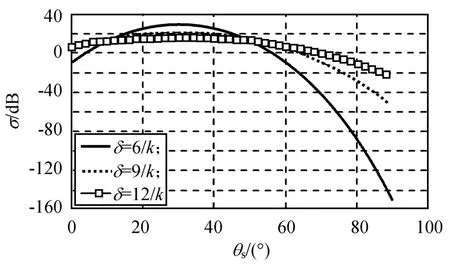
图3 粗糙面均方根对散射系数的影响(l=90/k,ε=20)Fig.3 Influence ofδonσ(l=90/k,ε=20)

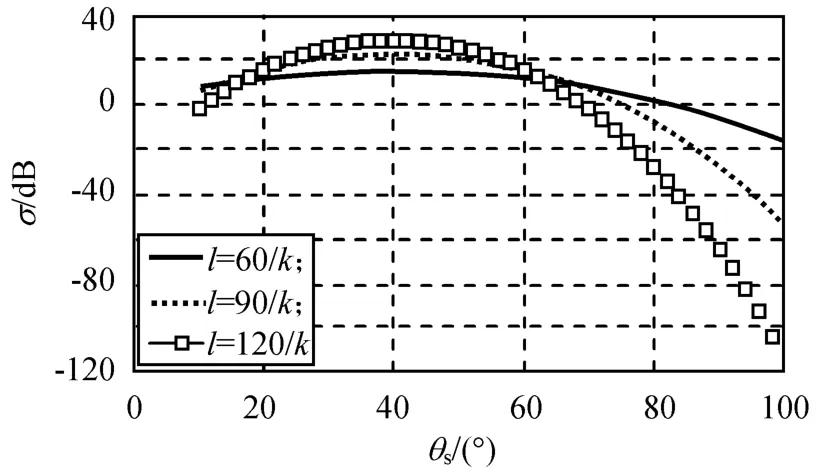
图4 粗糙面相关长度对散射系数的影响(δ=9/k,ε=20)Fig.4 Influence of l onσ(δ=9/k,ε=20)

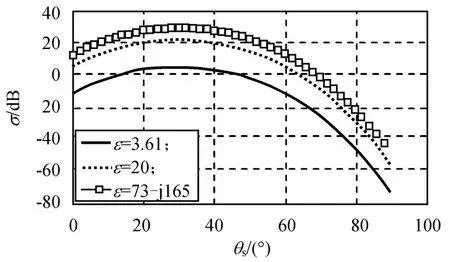
图5 介电常数对散射系数的影响(l=90/k,δ=9/k)Fig.5 Influenceofεonσ(l=90/k,δ=9/k)

由图3可知：当θs＜30°时,σ随θs增大而增大;当θs＞30°时,σ随θs增大而减小;当θs=30°时,σ达到一最大值。因θi=30°,故θs=30°对应镜反射方向,即在镜反射方向,σ达到最大。δ影响σ变化的快慢程度,δ越大,σ随θs的变化越慢;δ越小,σ随θs的变化越快,但均在θs=30°处σ出现最大值。

由图4可知：当散射角小于入射角(即θs＜30°)时,σ随θs增大而增大;当散射角大于入射角(即θs＞30°)时,σ随θs的增大而减小;在θs=30°时(镜反射方向),σ达到一最大值。l对σ的影响较大,l越大,σ随θs的变化就越剧烈;l越小,σ随θs的变化就越缓慢。

由图5可知：当散射角小于入射角(θs＜30°)时,σ随θs增大而增大;当散射角大于入射角(θs＞30°)时,σ随θs增大而减小;当θs=30°时(镜反射方向),σ达到一最大值。比较发现,当其他参数不变时,ε越大,σ就越大,且在散射角等于入射角时,均会出现σ最大值。

数值计算结果表明,VV极化条件下σ随θs的变化曲线与HH极化条件下几乎完全相同。

2.1.2 入射波波长对散射系数的影响

在θi=30°,θs=60°,φs=0°条 件下由式(8)～(12)、(22)、(26)、(27),用数值计算可得在粗糙面δ,l,ε一定时,不同λ的σ如图6所示。

由图6可知：因粗糙面为一维,故交叉极化的散射系数为零,仅有的HH、VV极化的σ均不随λ发生变化,另发现VV极化的σ大于HH极化。

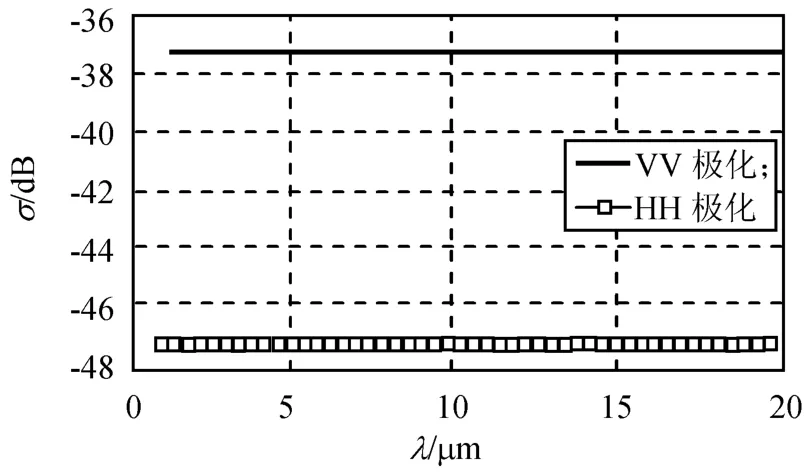
图6 入射波波长对散射系数的影响(l=90/k,δ=9/k,ε=3.61)Fig.6 Influence ofλonσ(l=90/k,δ=9/k,ε=3.61)

2.2 单站

2.2.1 粗糙面高度起伏均方根、相关长度、介质介电常数对后向散射系数的影响

在λ=1.06μm条件下,由式(23)～(27)可得粗糙面δ,l,ε对后向散射系数的影响分别如图7～9所示。

图7 均方根对后向散射系数的影响(l=90/k,ε=20)Fig.7 Influence ofδonσ(l=90/k,ε=20)

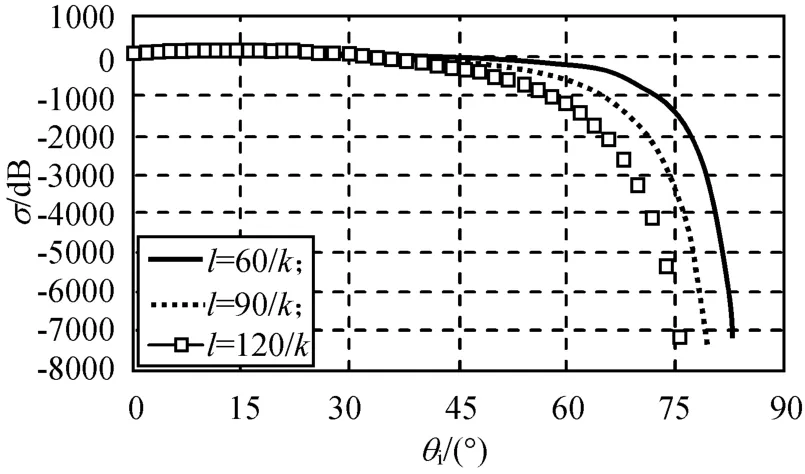
图8 相关长度对后向散射系数的影响(δ=90/k,ε=20)Fig.8 Influence of l onσ(δ=90/k,ε=20)

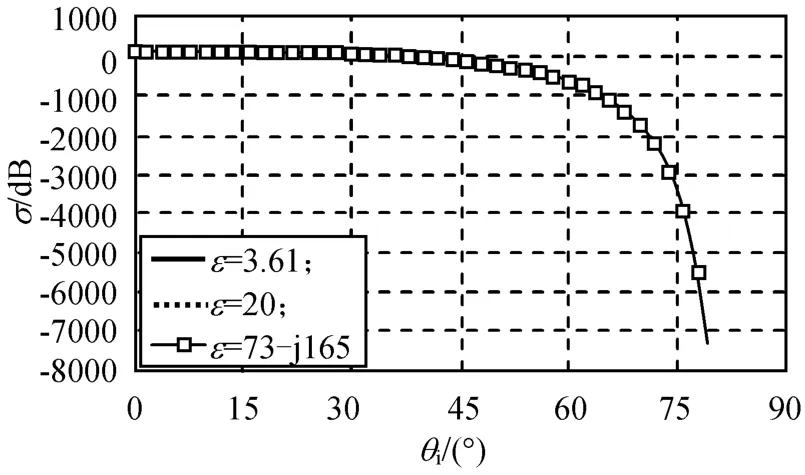
图9 介电常数对后向散射系数的影响(l=90/k,δ=9/k)Fig.9 Influence ofεonσ(l=90/k,δ=9/k)

由图7可知：后向散射系数σ随θi的增大而单调减小,当θi＜20°时不同δ的σ几乎重合,即当θi＜20°时,δ对σ的影响很小;当θi＞20°时,δ越大,σ越大,且随θi的变化越缓慢。另外δ越大,σ随θi急剧减小对应的入射角有增大的趋势。

由图8可知：σ随θi增大而单调减小,当θi＜30°时不同l的δ几乎重合,即当θi＜30°时l对δ的影响很小;当θi＞30°时,l越大,σ才明显地越小,且随θi变化越缓慢。另外l越小,σ随θi急剧减小对应的入射角有增大的趋势。

由图9可知：不同θi的σ几乎重合,表明介质的介电常数对后向散射系数的变化影响很小。另外,σ随θi增大而单调减小,在入射角变化的大部分范围内,σ随θi减小的趋势较慢,当θi＞60°时,σ随θi增大而急剧减小。

数值计算结果同样表明：VV极化时不同θi的σ与HH极化几乎完全相同。

2.2.2 入射波波长对后向散射系数的影响

由式(23)～(27),可得在粗糙面δ,l,ε相同时,不同λ的σ如图10所示。

由图10可知：因粗糙面为一维,故交叉极化的散射系数为零,HH、VV两种极化的σ均不随λ发生变化,且两种极化的σ数值相等。

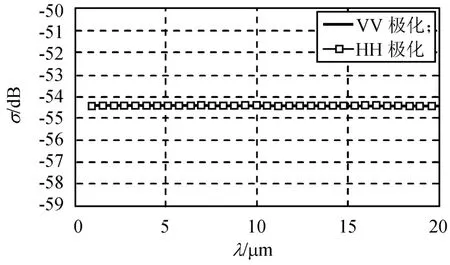
图10 入射波波长对后向散射系数的影响(l=90/k,δ=9/k,ε=20)Fig.10 Influence ofλonσ(l=90/k,δ=9/k,ε=20)

3 结束语

当光入射到一粗糙面上时,双站和单站在实际中均有重要应用,研究粗糙面散射系数的特征对复杂地、海背景散射与遥感的意义重要。本文用高斯型粗糙面模拟实际的粗糙面,根据微扰基尔霍夫法驻留相位法研究了该粗糙面的光散射,获得了高斯型粗糙面散射系数的基本特征和随波长变化特征,但仅限于一维情形,计算结果有待进一步的实验验证。对其他类型的粗糙面及二维粗糙面的散射还需作进一步的深入研究。

[1]ISHIMA RU A.Wave propagation and scattering in random medium[M].New York：Academic Press,1978.

[2]BASSF G,FUKS I M.Wave scattering from statistically rough surfaces[M].Oxford：Pergamon,1979.

[3]ULABY F T,MOORE R K,FUNG A K.Microwave remote sensing[M].London：Addision-Wesbey Publishing,1982.

[4]FUNG A K.Microwave scattering and emission models and their applications[M].London：Artech House,1994.

[5]OGILVY J A.Theory of wave scattering from random rough surface[M].Bristol：Institute of physics Publishing,1991.

[6]VORONOVICH A G.Wave scattering from rough surfaces(2nd ed.)[M].Berlin：Springer-Verlag,1999.

[7]GUO L X,JIAO L C,WU Z G.Electronmagnetic scattering from two-dimensional rough surface using the Kirchhoff approximation[J].China Phys.Letter,2001,18(1)：214-216.

[8]SULTAN-SALEM A K,TYLER G L.Validity of the Kirchhoff approximation for electromagnetic wave scattering from fractal surfaces[J].IEEE Transaction Geoscience Remote Sensing,2004,42(9)：1860-1870.

[9]BERIZZI F,MESE E D.Scattering coefficicient evaluation from a 2D seace[J].IEEE Transaction Antennas Propagat,2002,50：426-434.

[10]REN X C,GUOP L X.Study on optical wave scattering from slightly Gaussian rough surface of layered medium[J].Chinese Optics Letters,2007,5(10)：605-608.

[11]XIANG JS,HE J H.Mie理论的数值计算[J].应用光学,2007,28(3)：363-366.

[12]郑 毅,杨克成,夏 珉,等.气泡浓度对海洋激光雷达后向散射特性的影响[J].应用光学,2008,29(5)：785-788.

[13]陈 颖,王志良.一维小粗糙度表面上方物体的波散射[J].微波学报,2008,10(24)：53-59.