行波效应对大跨越输电塔－线体系纵向地震响应影响

魏奇科， 李正良

(重庆大学 土木工程学院，重庆 400045)

特高压输电塔－线体系是一种重要的电力设施［1，2]，地震作用下它的破坏现象时有发生，从而导致供电系统的瘫痪［3]，这不仅严重影响人们的生产生活秩序，还会造成重大的次生灾害，给社会和人民生命财产造成严重的后果。大跨越输电塔是一种柔性的高耸结构，地震作用下，输电塔和导线之间的耦联作用不可忽略［4，5]。岳茂光等［6]研究一致输入下大跨度输电塔一导线体系地震反应特性，特高压大跨越输电塔－线体系的跨度一般都比较大，达到几百米甚至超过千米，地震波以有限波速传播时，各个点的地震动存在明显的差异，这一点已被许多强震观测记录所证实［7，8]。许多学者对大跨越输电塔－线体系的行波效应或者多点激励进行了研究［9－12]，得出了一些有意义的结论。但是这些文献采用的都是简化的杆索计算模型，对于实际复杂的三维输电塔模型，考虑到塔－线体系的约束条件及强烈的几何非线性，这些结论是否适用，还需建立精细的三维空间有限元模型进行研究，并且以往对行波效应的分析仅计算有限几种行波波速工况，以致不能全面概括行波效应对输电塔－线体系地震响应的影响和揭示影响的机理。因此，为了正确分析行波效应对输电塔－线体系地震响应的影响，建立了输电塔－线耦联体系精细的三维空间有限元模型，运用几何非线性动力时程分析方法研究了纵向地震作用下大跨越输电塔－线体系的响应特性，并和一致地震动输入下的反应进行了对比，揭示了行波输入下输电塔－线体系地震反应的机理。

1 基本方法与原理

1.1 一致地震作用下塔－线体系求解方法

在一致地震作用下，考虑导(地)线刚度矩阵随时间变化的塔－线体系动力平衡方程为:

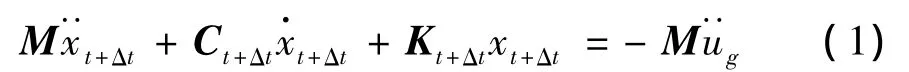
1.2 多点地震输入增量运动方程

如果考虑不均匀地面激励问题，运动方程为:

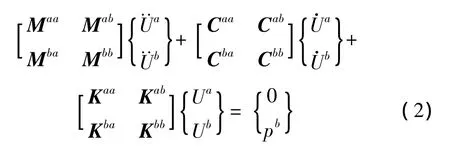
式(2)分离表示得到:

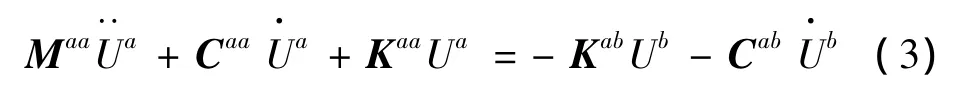
由于一般情况下，阻尼矩阵Cab很难确定，因此在公式推导时阻尼力常被省略［13]，可以得到:

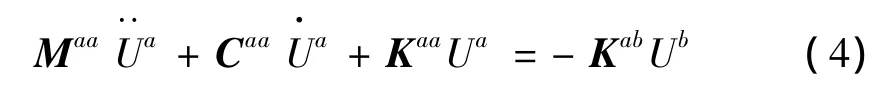
式(4)即为地震激励下塔－线体系结构分量Ua的位移输入模型。其中，方程右边的Ub即需要输入的结构各支座处地面运动位移，对于不同的支座Ub不同，由支座输入地震波的情况决定。

2 计算模型分析

2.1 塔—线耦联体系三维有限元模型的建立

本文建立的塔－线耦联三维有限元模型是根据汉江大跨越1 000 kV交流特高压线路工程建立的，包括两个输电塔和三跨导(地)线，输电线共分三层，最上层是两根地线，中间为一根六分裂导线，下层为两根六分裂导线，输电线与输电塔通过悬挂式绝缘子连接，为两塔三线模型，建模使用的是国际通用程序 ANSYS 11.0。汉江大跨越线路工程是晋东南～南阳～荆门交流1 000 kV输变电线路试验示范工程中的重大项目，工程全长2 956 m，跨越档距1 650 m，铁塔全高181.8 m，单基重量1 100 t，是单基铁塔中最高最重和技术难度最大的大跨越工程。

该塔结构为格构式组合角钢塔，角钢端部采用螺栓连接。因此理想的计算模型应该是在桁架平面内杆件铰接，平面外刚接。从有限元角度来看，即放松平面内自由度，约束平面外自由度。但一般输电塔杆件角度复杂多样，单元边界条件操作极其繁琐;且有大量学者证明刚接节点处理与铰接节点处理的计算结果相差极小，本文中的输电塔均采用刚接连接。角钢材料主要为 Q420钢和 Q235钢，在 ANSYS中采用空间梁(Beam188)单元模拟。输电塔的节点板及其它连接构件对结构刚度无影响，在建模中仅考虑其质量，以质量单元(Mass21)来模拟。每个输电塔的底部4个节点和两端导线的6个节点采用固定约束。

因为导(地)线是空间柔性结构，且带有初始应变，所以对它建模首先要涉及导(地)线的找形问题。由于导(地)线初始时刻存在微小的初应变，导致内部存在应力和初始张力，在计算前需要寻找初始时刻导(地)线的位形。电线的悬挂曲线方程式一般有悬链线、斜抛物线和平抛物线三种模型［14]。其中悬链线模型假设电线荷载沿线长均匀分布，斜抛物线模型假设电线荷载沿悬挂点连线均匀分布，平抛物线模型假设电线荷载沿悬挂点间的水平线均匀分布。文献［15] 指出，使用平抛物线公式与使用悬链线公式相比，应力误差在2%左右，因此出于简化考虑，本文采用平抛物线模型来模拟导地线的悬挂曲线。如图1所示，A和B两点为电线的两个悬挂点，将坐标原点定义为左悬挂点A，则电线悬挂曲线方程式为:

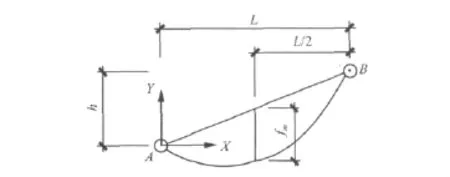
图1 导线曲线坐标系Fig.1 Coordinate system of the wire curve

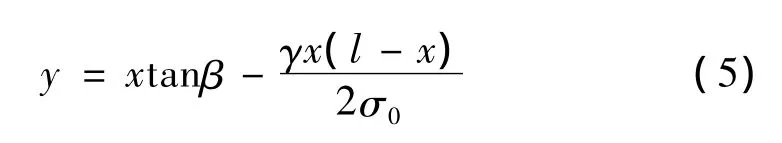
其中:

式中，l为挡距(两悬挂点间的水平距离m);h为高差(两悬挂点间的垂直距离m);β为高差角，tanβ=h/l;fm为电线最大弧垂(两悬挂点连线中点到电线的垂直距离m);σ0为电线各点的水平应力(即最低点的应力N/m2);γ为电线比载(即单位长度单位截面上的荷载N/m·m2);

在纵向地震多点激励计算时，采用大质量法。在ANSYS 11.0中建立了输电塔－线体系三维有限元模型。如图2所示。

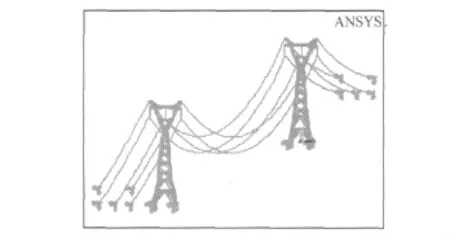
图2 输电塔－线体系三维有限元模型Fig.2 3D finite element model of power transmission tower-cable system

2.2 塔、线控制截面的选取

取跨越塔为研究对象，塔、导线的控制截面取法如下:① 塔身位移:取导(地)线或绝缘子与大跨越塔身相连的点，从高到低依次为TU1、TU2和TU3;② 塔身内力:取跨越塔一层、三层和六层角部的主材 TN1、TN2、和TN3为控制截面;③ 导(地)线位移:取导(地)线大跨越跨中竖向位移;④ 导(地)线内力:取导(地)线两端悬挂点的内力。

2.3 地震动输入

考虑波传播速度的各种可能性，取视波速为400 m/s～8 000 m/s。因此可取地震波纵向传播通过大跨越两端输电塔的时间间隔为0.2 s～4.0 s共21种工况来考虑行波效应即相位差对塔－线体系地震反应的影响。一致地震输入可以看作视波速无穷大的特例。输入地震动时，本文选用了常用的El Centro波，地震动加速度峰值都调整为0.15 g。

3 行波效应下塔—线体系响应

3.1 行波效应下输电塔响应分析

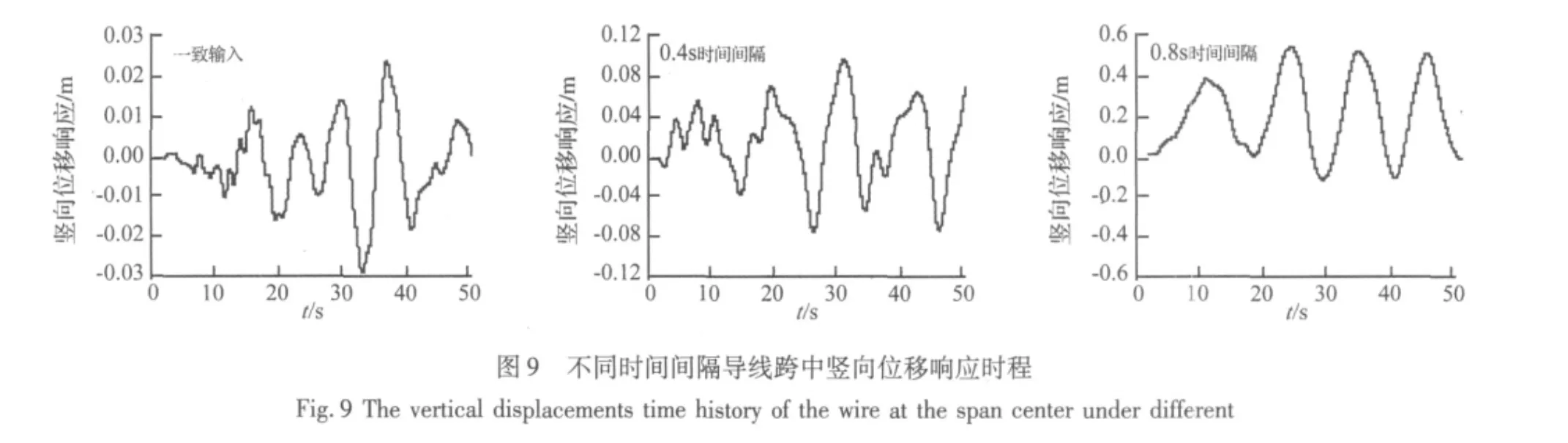
本文研究了在多点输入和一致输入情况下输电塔－线体系塔身纵向响应，并进行了分析比较。行波波速、地震动性质、输电塔档距以及输电塔－线体系中导(地)线的松紧程度等都对输电塔－线体系的行波效应产生影响，如文献［11] 所述。假定输电塔的档距与到震源的距离相比很小，地震波的衰减可以忽略，则前面的影响因素可以主要归结为不同输电塔受到地震波作用时间间隔的影响，即相位差的影响。图3给出了不同时间间隔下塔身控制点TU1、TU2以及TU3纵向最大位移比;图5给出了不同时间间隔下塔身控制点TU1的位移时程。

图3 塔身控制点最大位移比Fig.3 The maximal displacement ratio of transmission tower’s control points

从图3可以看出，和一致地震动输入相比，不同时间间隔的行波输入对输电塔的最大位移响应类似于结构振动曲线，有增大有减小，剧烈程度随着时间间隔增大而衰减。一致地震输入即时间间隔为0时，大跨越导线两端的跨越塔振动基本一致，导线的影响很小。随着时间间隔的增加，对应的地震波波速逐渐减小，行波效应对塔身位移响应影响的剧烈程度逐渐减小，由图可以推测随着时间间隔进一步增大趋于无穷，导线两端的塔各自分别受地震作用的极限情况，那么最大位移比趋于1.0，对塔身而言，与一致输入的情况基本相同。

由图3的波动曲线还可以看出，最大位移比随时间间隔的增加而周期性变化，变化的周期基本为1 s，这与单塔的一阶周期(0.947 s)十分接近，当时间间隔正好为单塔一阶周期整数倍加一半时，塔身位移响应最大，行波效应对输电塔将最不利，塔身最大位移比达到1.27;当时间间隔正好为单塔一阶周期的整数倍时，塔身位移响应最小，行波效应反而是有利的，最大位移比减小为0.88。

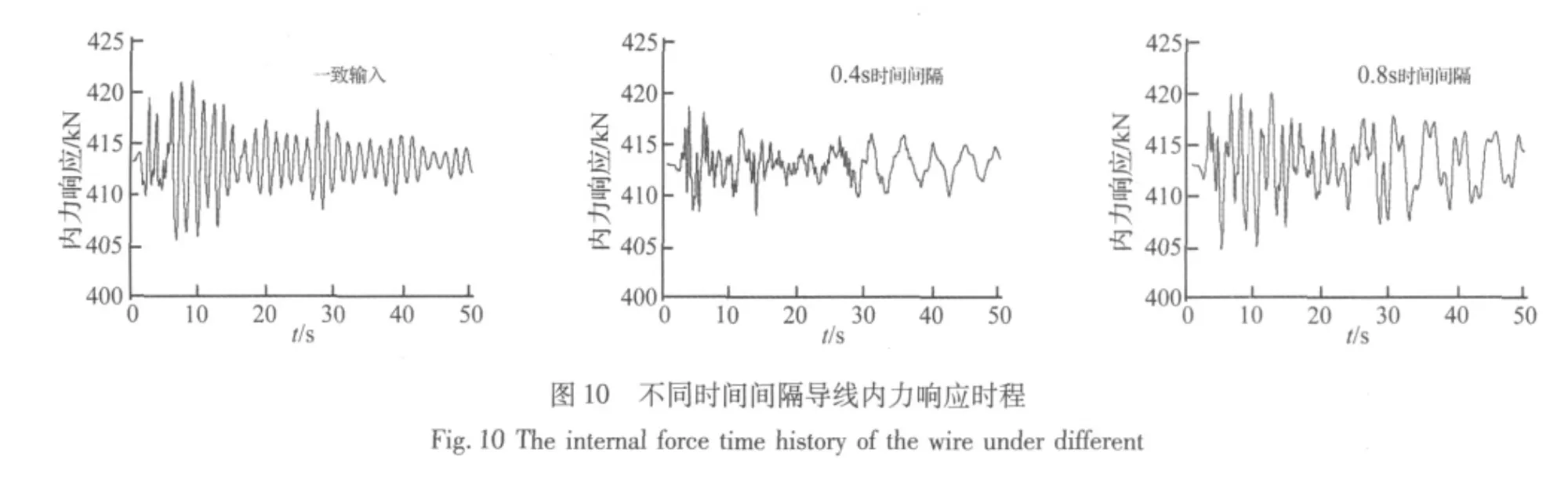
地震动作用下，输电塔－线体系的内力响应包含重力作用和地震作用两种荷载作用的影响。不同的地震动输入，地震作用和重力作用对输电塔－线体系的影响大小将有很大的不同。因此，为了消除重力作用对本文输电塔－线体系行波效应分析的影响，本文对应地震作用下输电塔的内力分析针对内力响应的幅值而非最大最小值，即总的内力响应扣除重力作用下静响应的部分。图4给出了不同时间间隔下塔身控制点TN1、TN2以及TN3内力响应幅值比;图6给出了不同时间间隔下塔身控制点TN1的内力响应脉动部分时程;

从图4可以看出，塔身内力响应幅值比与最大位移比的规律相同。大跨越导线两端输电塔相位一致时，内力幅值略有减小，最小达到0.88;而相位相差半周期时，行波输入加大了地震反应，内力幅值比最大可达1.27。

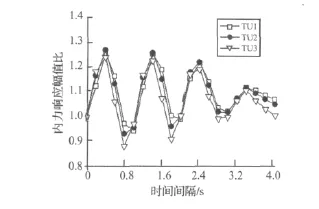
图4 塔身控制点内力响应幅值比Fig.4 The internal force amplitude ratio of transmission tower’s control points

3.2 行波效应下导(地)线响应分析

为了更好地分析行波效应对导(地)线的影响，本文选取导(地)线跨中竖向最大位移作为分析对象，如图7所示。而分析纵向位移实际意义不大，本文不作考虑。

由图7可以看出，行波输入时，导(地)线的竖向位移比一致输入时大很多。一致输入时，导(地)线跨中竖向位移仅为约0.02 m;而行波输入时间间隔为0.8 s时，导(地)线跨中竖向位移达到0.2 m，增大了10倍;当时间间隔为4 s时，导(地)线跨中竖向位移更是达到了0.5 m，增大了约25倍。由此可见，导(地)线竖向位移在行波输入下反应十分强烈。

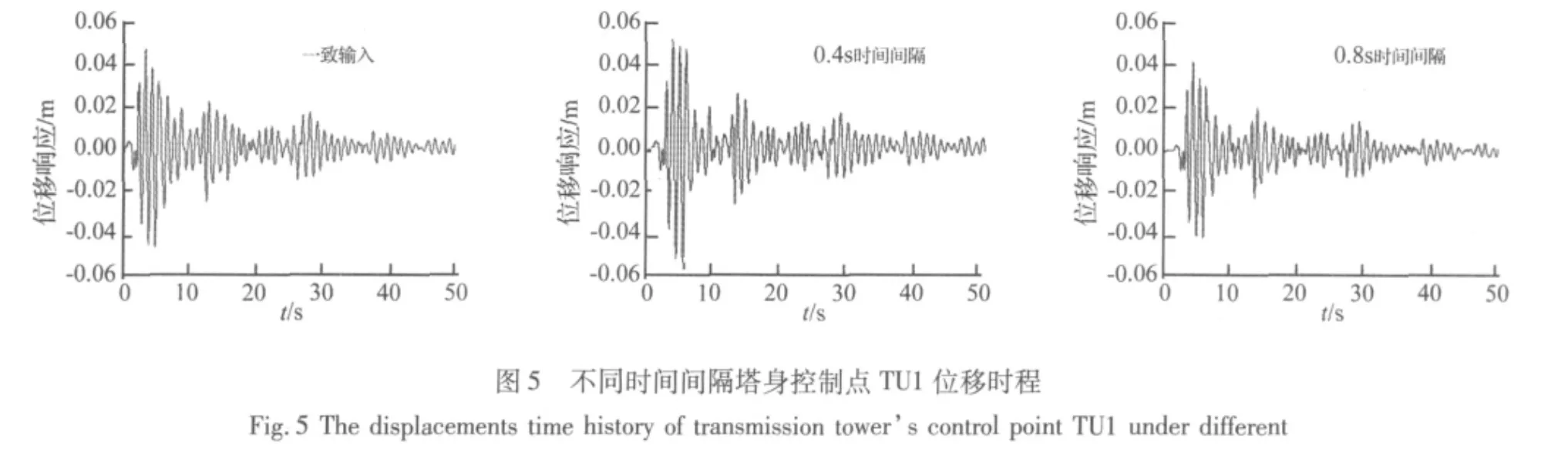
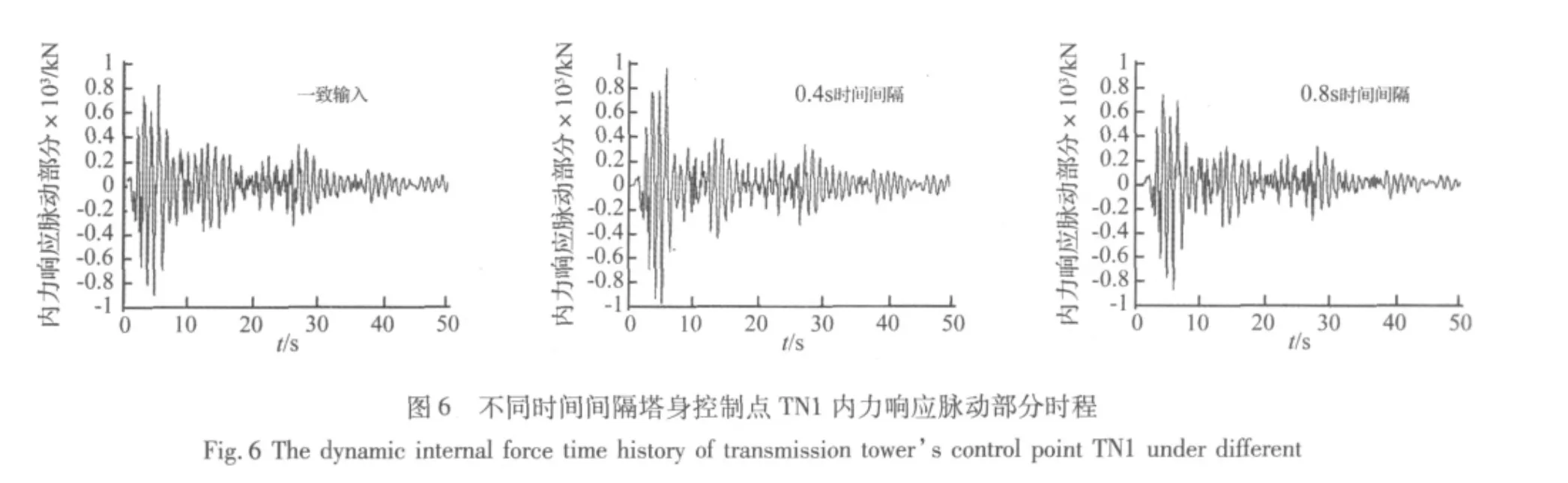
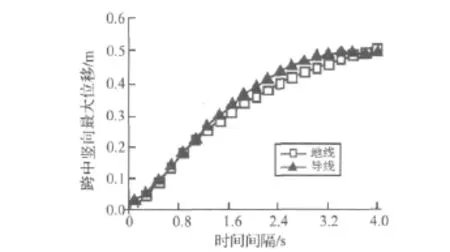
图7 导(地)线跨中竖向最大位移Fig.7 The vertical maximal displacement of the wire at the span center

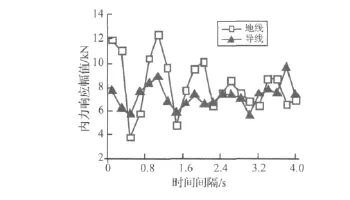
图8 导(地)线内力响应幅值Fig.8 The internal force amplitude of the wire

同时由图9导线跨中竖向位移时程曲线可知，一致输入时，位移时程中高频成分较多，曲线“锯齿”较明显，随着时间间隔增大，曲线越来越光滑，并且频率成份越来越单一，趋近导线的一阶频率。由图7及图9推测，随着时间间隔的进一步增大，导(地)线跨中竖向位移时程将逐渐趋于简谐振动正弦曲线，频率为导线的一阶频率，幅值趋于稳定。

由图8可知，与一致输入相比，行波输入下地线内力响应幅值随时间间隔的曲线同塔身的响应正好相反，当地震波作用于大跨越两端输电塔的相位差半周期时，内力响应的幅值有所减小，正好“合拍”时，如一致输入时，则地线响应幅值较大。同时随着时间间隔的增加，内力响应幅值的波动程度越小，最后趋于平稳。而导线由于有绝缘子悬挂，相当于有了隔震减震的作用，因此导线的地震响应很小，但也有与地线基本相同的规律。总的来说，由于导(地)线属于极柔的结构体系，地震响应较小，与导线的静内力相比，由图10导线的内力响应时程可以看出，约在5%以内。因此行波效应对导(地)线的内力响应基本可以忽略。

4 结论

(1)行波输入与一致输入相比既可以增加又可以降低输电塔的地震反应，主要与地震动作用于大跨越两端输电塔的时间间隔即相位差有关。

(2)当相位差为单塔一级周期一半时，行波效应对输电塔将最不利，塔身纵向最大位移比以及构件内力响应幅值比将达到1.27;当时间间隔正好为单塔一阶周期的整数倍时，塔身地震响应最小，与一致输入相比行波效应下塔身最大位移比和内力响应幅值比减小为0.88。

(3)行波输入时，导(地)线的竖向位移比一致输入时大很多，设计时要特别注意。

(4)由于导线属于极柔的索结构体系，同时由绝缘子悬挂约束较小，地震响应较小，与导线的静内力相比，约在5%以内。行波效应对导(地)线的内力响应基本可以忽略。

［1] 郭剑波.“八五”期间我国电网稳定事故统计分析［J] .电网技术，1998，22(2):72 －74.

［2] 屈 靖，郭剑波.“九五”期间我国电网稳定事故统计分析［J] .电网技术，2004，28(21):60 －62，68.

［3] 谢 强，李 杰.电力系统自然灾害的现状与对策［J] .自然灾害学报，2006，15(4):126 －131.

［4] 李宏男，陆 鸣，王前信.大跨越自立式高压输电塔－电缆体系的简化抗震计算［J] .地震工程与工程振动，1990，10(2):73－87.

［5] 李宏男，石文龙，贾连光.考虑导线影响的输电塔侧向简化抗震计算方法［J] .振动工程学报，2003，16(2):233－237.

［6] 岳茂光，王东升，李宏男，等.近断层地震动作用下输电塔一导线体系反应分析［J] .地震工程与工程振动，2005，25(4):116－125.

［7] 屈铁军，王前信.多点输入地震反应分析研究的进展［J] .世界地震工程，1993(1):30－36.

［8] 潘旦光，楼梦麟，范立础.多点输入下大跨度结构地震反应分析研究现状［J] .同济大学学报，2001，29(10):1213－1219.

［9] Ghobarah A，Aziz T S，El-AttarM.Response of transmission lines to multiple support excitation ［J] . Engineering Structures，1996，18(12):936－946.

［10] 岳茂光，李宏男，王东升，等.行波激励下输电塔–导线体系纵向地震反应分析［J] .中国电机工程学报，2006，26(23):145－150.

［11] 田 利，李宏男，黄连壮.多点激励下输电塔–线体系的侧向地震反应分析［J] .中国电机工程学报，2008，28(16):108－144.

［12] 全 伟，李宏男，岳茂光.多点激励下输电塔－导线体系纵向地震反应分析［J] .振动与冲击，2008，27(10):75 －80.

［13] Wilson E L.Three dimensional static and dynamic analysis of structures:a physical app roach with emphasis on earthquake engineering［M] .Computers and Structures，Inc，Berkley，California，2002.

［14] 张殿生.电力工程高压送电线路设计手册［M] .北京:中国电力出版社，2005.

［15] 邹天晓.架空送电线路的电线力学计算［M] .北京:水利电力出版社，1987.