矩形截面高层建筑气动基底扭矩系数均方根值研究
顾 明,张正维,2,全 涌,熊 勇
(1.同济大学 土木工程防灾国家重点实验室,上海 200092;2.南通大学 建筑工程学院,江苏 南通 226019)
在高层建筑抗风研究中,通常将风荷载分为顺风向、横风向和扭转方向三个分量,相对而言,人们对高层建筑扭转方向风荷载的了解程度远不及顺风向风荷载与横风向风荷载。如果高层建筑结构的厚宽比较大,或结构不对称或结构的扭转自振频率接近平动自振频率,风致扭转效应将成为结构设计不可忽略的一部分;同时高层建筑的扭转振动能加剧截面边沿的位移和加速度,且居住者对房屋的扭矩运动特别敏感,因此高层建筑的扭转风振响应应该引起设计者的重视[1,11]。扭转向风致响应研究的一般方法是:首先通过风洞试验得到气动扭矩,然后根据随机振动理论得到结构的扭转风致响应,最后给出工程师进行结构设计所需要的扭转向等效静力风荷载[1]。在计算扭转风振响应的过程中,一般将扭转风振响应分为背景分量与共振分量来计算,计算背景响应时需要气动基底扭矩系数均方根值,计算共振响应时需要气动基底扭矩系数的功率谱。由于篇幅的限制,本文只对气动基底扭矩系数均方根值进行研究,其功率谱将在专门的文章进行介绍。
从20世纪90年代起,对结构风致扭转响应的研究逐渐增多,取得了一些比较有意义的成果,表1给出了矩形截面高层建筑基底扭矩系数均方根值的国内外研究成果。国内外的主要研究如下:
Marukawa[2,5]通过高频测力天平试验给出了基底扭矩系数均方根值的计算公式,并且考虑了风场的影响。Liang[9]通过测压试验拟合得到了基底扭矩系数均方根值,但是该值是分层叠加得到,其中选用的无量纲风速为每层测点高度处的风速,而不是通用的选择顶部高度处的风速。AIJ[7]给出了基底扭矩系数均方根值的计算公式,但是没有考虑长细比与风场的影响。唐意[11]采用刚性模型测压试验给出了层扭矩系数均方根值的计算公式,考虑了厚宽比与风场的影响。Ha[10]通过高频测力天平试验给出了基底扭矩系数均方根值的计算公式,没有考虑长细比与风场的影响。
Choi[3],Yutaka[6],以及 Zhou[8]也对矩形截面高层建筑基底扭矩系数均方根值进行了研究,但是没有给出相应的拟合公式。
本研究在风洞中采用高频测力天平进行了4类不同风场71个典型建筑模型的风洞试验,对高层建筑基底扭矩系数均方根值进行了细致、全面的研究,考察了截面厚宽比、模型长细比和风场对基底扭矩系数均方根值的影响,拟合得到了基底扭矩系数均方根值的经验公式,通过与国内外研究成果的比较,对拟合公式的可使用性进行了评估,为高层建筑的结构设计及相关荷载规范的制定和修改提供了很好的参考。
1 风洞试验概况
1.1 试验设备及模型概况
本试验在同济大学土木工程防灾国家重点试验TJ-1大气边界层风洞中进行,风洞试验段高1.8 m,宽1.8 m,长18 m,风速范围为1 m/s-30 m/s,连续可调。试验模型由50 mm×50 mm,厚度为1mm的铝棒为芯棒来提供刚度,外部采用泡沫塑料试验建筑不同外形的模拟,从而使模型质量小而刚度大,以确保天平-模型系统有足够高的固有频率。试验所采用天平基底弯矩与扭矩的量程为30 Nm,测量精度为0.004 Nm,测量精度很高。试验的采样频率为600 Hz,采样时间为60 s。

表1 基底扭矩系数均方根值研究成果Tab.1 Research results of RMSvalues of base torsional moment coefficient

表2 试验模型参数Tab.2 Parameters of experiment models
1.2 试验数据处理
利用高频天平测力技术在风洞中对建筑模型的气动力进行测量时,要求天平模型系统具有较高的频率。本课题试验中所有天平模型系统的一阶振型中扭转向的固有频率都大于130 Hz,远远高于风荷载谱密度的频率范围,模型自身的振动引起的模型荷载测量上的误差就可以忽略不计。对于基底扭矩谱无需像横风向与顺风向基底弯矩谱一样进行修正以减小天平模型系统频率不够高而对风荷载谱产生的放大作用。

本文无量纲的气动力系数定义如式(1)所示:

其中,C'MT为基底扭矩系数均方根值,为顶部来流风压,B为建筑的迎风面宽度(特征宽度),H为建筑的迎风面高度,σTz为基底扭矩的均方根。
1.3 试验结果合理性验证
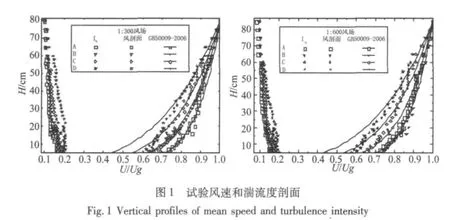
为了验证本试验结果的合理性,图2给出了本文结果与国内外主要成果的比较。从图中可以看出,在C类情况下,各种试验的湍流强度以及分剖面指数比较接近,本文的试验结果与国内外主要研究成果有很好的一致性;在D类风场下,在厚宽比D/B>2的情况下,本文的试验结果比Marukawa[2]的试验结果偏大,主要是由于本文D风场的湍流度比 Marukawa[2]的湍流度偏大,研究表明:当厚宽比D/B>2后,扭转气动力的主要受紊流强度与重附着流的影响,增大紊流度能显能够使重附着流提前发生,从而使基底扭矩系数均方根值变大。本文试验结果与前人的大量试验具有很好的一致性,从而说明本文的试验方法以及数据处理方法是合理可行的。
2 试验结果
图3~图5给出了所有71个不同模型在A,B,C,D四类风场中0°与90°风向角下基底扭矩系数均方根值随厚宽比、长细比与风场类型的变化规律。
2.1 厚宽比的影响
图3给出厚宽比对基底扭矩系数均方根值的影响。从图中可以看出,在一定长细比与风场类型下,基底扭矩系数均方根值随D/B的增大而单调增加。当模型厚宽比D/B<1时,基底扭矩系数均方根值随着厚宽比的增大而增大,但是增大幅度不大,这主要是由于当厚宽比D/B<1时,扭转气动力主要是由横风向的旋涡脱落引起的;当厚宽比D/B>1后,基底扭矩系数均方根值迅速增大,且递增的趋势逐渐加剧,这主要是由于当厚宽比D/B>1后,扭转气动力主要是由尾流与再附着流引起的横风向不对称压力而产生的,这一结论与Tamura(1996)的结论是一致的。
2.2 风场的影响
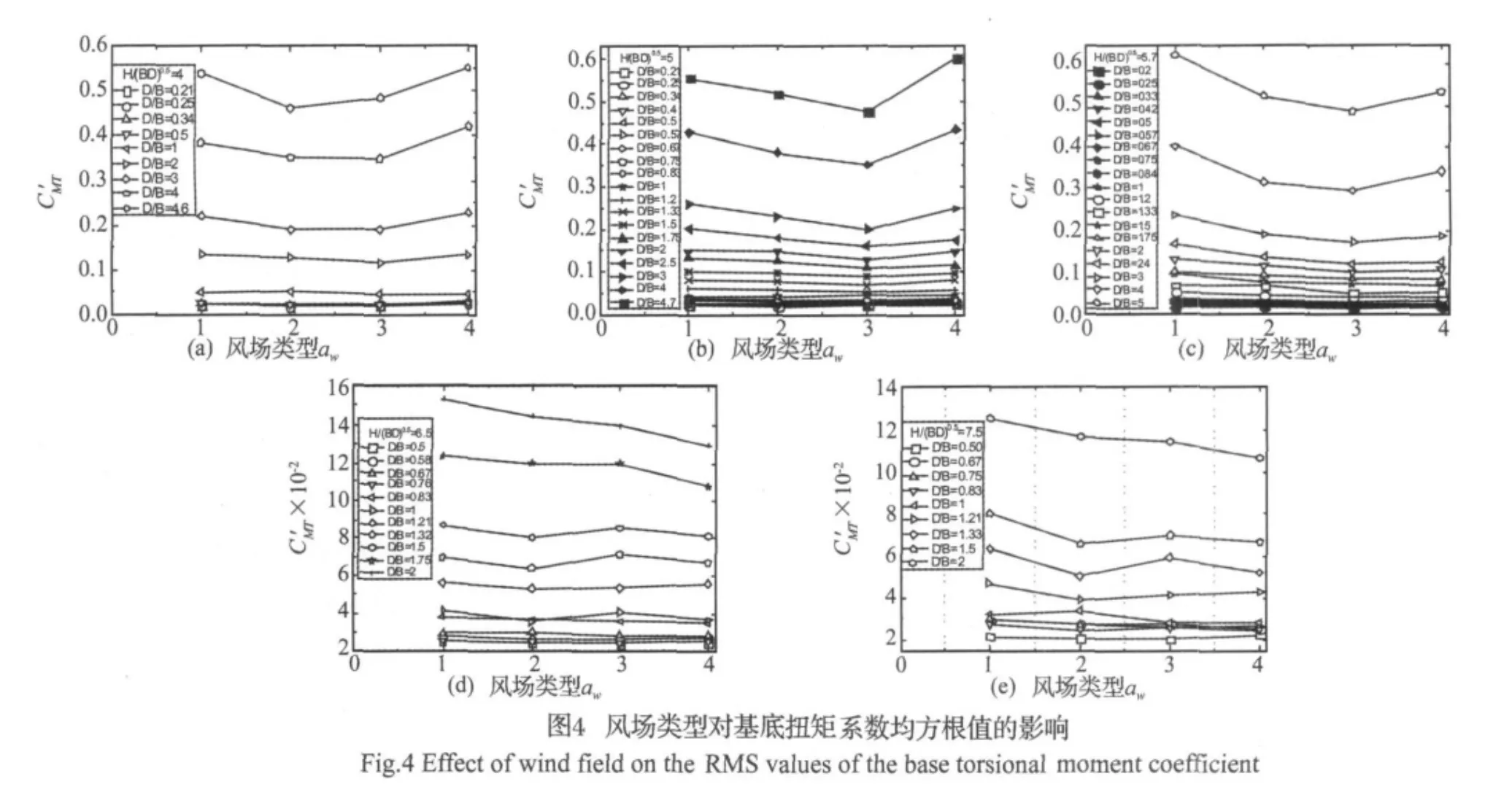
图4给出了风场类型对基底扭矩系数均方根值的影响。从图中可以看出,当厚宽比D/B≤2时,基底扭矩系数均方根值受厚宽比的影响较小,这主要是由于当厚宽比D/B≤2时,扭转气动力主要是由于横风向的旋涡脱落引起的不对称力而导致的,迎风面来流紊流的不对称作用也对扭转动荷载的贡献较小;当厚宽比D/B>2后,基底扭矩系数均方根值随着湍流度的增大,先减小后增大,这主要是由于随着厚宽比的增大,再附着流出现,湍流度的增大同时又加快了重附着流的出现,并且减小了旋涡脱落的强调,同时来流紊流的不对称作用也对扭转动荷载的贡献也越来越大,这样就导致了随着湍流度的增大,基底扭矩系数均方根值先减小后增大。
2.3 长细比的影响
从图4中可以看出,在一定的长细比下,风场类型对基底扭矩系数均方根值的影响随着厚宽比D/B的不同而变化,不同长细比下风场类型对基底扭矩系数均方根值的影响在不同的厚宽比下基本一致,说明长细比对基底扭矩系数均方根值的影响不大。
2.4 拟合公式
根据上文的分析,基底扭矩系数均方根值的主要影响因素为厚宽比与风场类型(湍流强度),长细比的影响比较小,可不予考虑。为了便于工程应用,基于上述试验数据处理的结果,利用多参数的最小二乘法,拟合得到如下矩形截面基底扭矩系数均方根值的函数表达式:

其中,αdb=D/B为建筑的厚宽比,B和D分别为建筑的迎风立面宽度和顺风向厚度;αw为风场类型,1,2,3,4分别代表A,B,C,D四类风场。
为了能更好地量化分析拟合公式的误差,定义误差率如下:

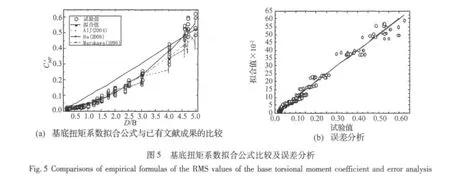
图 5(a)中给出了本文拟合公式与 AIJ[7]、Ha[10]以及 Marukawa[5]的比较结果。Ha[10]公式计算结果比其他结果都要大,该拟合公式的计算结果较保守;当厚宽比小于3时,本文的拟合结果与试验结果以及AIJ[7]和Marukawa[5]的计算结果都有很好的一致性;当厚宽比大于3 后,本文的计算结果比 AIJ[7]和 Marukawa[5]的计算结果稍有偏大,这主要是由于试验风场条件不同而导致的微小差别。图5(b)对拟合公式(2)的准确性进行了分析。可以看出试验值比较均匀地分布于代表拟合值的直线的上下侧,公式(2)的误差率的平均值为0.38%,标准差为10.1%,拟合公式有很好的预测试验结果。总之,式(2)计算结果不仅与原始数据相符,与其他文献试验结果比较也有较好的一致性,说明本文的拟合公式具有较高的准确性和可信度。
3 结论
本文利用高频动态测力天平技术,在4种不同风场中对71种不同尺寸的矩形截面高层建筑刚性模型进行了测力试验,对矩形截面高层建筑基底扭矩均方根系数进行了研究,得到了以下一些有意义的结论:
(1)在长细比与风场类型一定的情况下,基底扭矩系数随D/B的增大而单调增加。当厚宽比D/B<1时,扭转气动力主要是由横风向的漩涡脱落引起的,基底扭矩系数增幅不大;当厚宽比D/B>1后,扭转气动力主要是由尾流与重附着流引起的横风向不对称压力而产生的,基底扭矩系数迅速增大,且增大的趋势逐渐加剧;
(2)在一定的长细比下,风场类型对基底扭矩系数的影响随着厚宽比D/B的不同而不同。当厚宽比D/B≤2时,基底扭矩系数受厚宽比的影响较小;当厚宽比D/B>2后,基底扭矩系数随着湍流度的增大,先减小后增大;
(3)长细比对基底扭矩系数的影响较小,在实际应用中可以不予考虑;
(4)本文给出的拟合公式考虑了厚宽比与风场类型对矩形截面高层建筑基底扭矩系数的影响,该经验公式形式简单,并且具有较高的准确性与可信度,可为实际应用及规范修订提供参考。
[1] Simiu E,Scanlan R H.Wind effects on structures[M] .3rded.New York:John Wiley& Sons Ltd,1996.
[2] Marukawa H,Ohkuma T,Momomaura Y.Across-wind and torsional acceleration of prismatic high rise buildings[J] .Journal of Wind Engineering and Industrial Aerodynamic,1992,41 -44:1139 -1150.
[3] Choi H,Kanda J.Proposed formulae for the power spectral densities of fluctuating lift and torque on rectangular 3-D cylinders[J] .Journal of Wind Engineering and Industrial Aerodynamic,1993,46 -47:507 -516.
[4] Tamura Y,Kawai H,Uematsu Y,et al.Wind load and windinduced response estimations in the Recommendations for Loads on Buildings,AIJ 1993[J] .Engineering Structures,1996,18(6):399-411.
[5] Marukawa H,Ohkuma T.Formula of fluctuating wind forces for estimation of across-wind and torsional responses of prismatic high rise buildings[J] .Journal of Structural Construction Engineering of Japan,1996,482:33 -42.
[6] Yutaka A,Koji K,Kazuki H.Experimental research of aerodynamic force on rectangular prism[J] .Journal of Wind Engineering of Japan,2002,91:83-88.
[7] Architectural Institute of Japan.AIJ Recommendations for Loads on Buildings(English version)[M] .2004.
[8] Zhou Y,Kijewski H,Kareem A.Aerodynamic loads on tall building:Interactive database[J] .Journal of Structural Engineering,2003,129-394.
[9] Liang SG,Li Q S,Liu SC,et al.Torsional dynamic wind loads on rectangular tall buildings[J] . Engineering Structures,2004,26:129.
[10] Ha Y C,Kim Y S,Kim H R.Fluctuating torsional moment coefficient and power spectral density coefficient for estimating wind loadings on a tall building[C] .Proceedings of the 4th International Conference on Advances in Wind and Structures(AWAS'08),Jeju,KOREA,May 29 -31,2008.
[11] 唐 意.弯扭耦合高层建筑风致振动及静力等效风荷载[D] .上海:同济大学土木工程学院,2006.

