PolyMAX模态参数识别算法的快速实现

孙鑫晖， 郝木明， 王淮维

(中国石油大学(华东)化学工程学院，山东 东营 266555)

实验模态分析经历了几十年的发展历程，已经从单自由度发展为多自由度，由单输入单输出发展为多输入多输出，由局部估计发展为整体估计［1]，并且新的识别方法不断出现。其中PloyMAX方法［2，3]是近几年发展起来的频域识别算法，该方法也称作多参考点最小二乘复频域算法(poly－reference least square complex frequencydomain)［4]。由于比较好的解决了频域算法中数值病态问题，该方法可以处理很宽的频率范围和很高的模态阶次。并且能够产生非常清晰的稳定图，适用于大阻尼与高噪声数据，目前已经成为一种工业标准。

本文通过分析该算法实现过程中的矩阵结构，给出了缩减正则方程的近似计算方法，从而避免了矩阵求逆以及乘法运算，使得计算量大为降低，提高了模态参数识别速度。

1 PolyMAX算法描述

1.1 频响函数的右矩阵分式模型

对于一个具有No个输出，Ni个输入的多输入多数出系统(MIMO)，系统的频响函数 H(ω)∈CNo×Ni可以通过右矩阵分式模型进行描述:

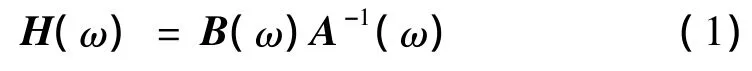
其中矩阵多项式 B(ω)∈CNo×Ni、A(ω)∈CNi×Ni定义为:

其中 Ωj(ω)=exp(－iωTs·j)为基函数(Ts为采样周期)，n为模型阶次，Aj、Bj(j=0…n)矩阵多项式系数。

1.2 正则方程的缩减

通过对式(1)右乘A(ω)进行线性化处理，然后利用最小二乘法求解系数矩阵。但是直接求解存在以下缺点是:

(1)当频响函数规模较大、模型阶次较高时导致正则方程的维数太高，直接求解难以实现。

(2)分母系数矩阵Aj不能独立于分子系数矩阵Bj求解，而模态参数的求解只需要分母系数矩阵Aj。

文献［4] 给出了一种通过缩减正则方程求解分母系数矩阵的方法，该方法能够大幅减小正则方程的维数且无需求解分子系数矩阵Bj。这里给出缩减正则方程的表达式，具体推导参见文献［4] 。

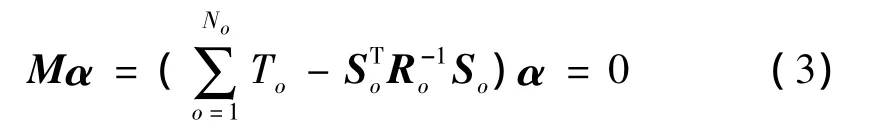
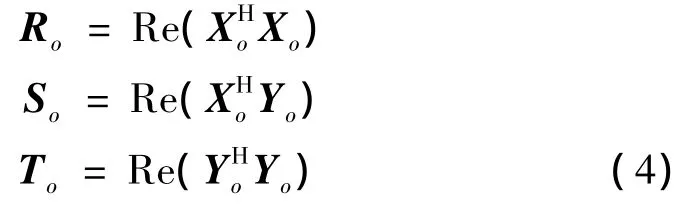
式(4)中Xo、Yo的表达式如下:

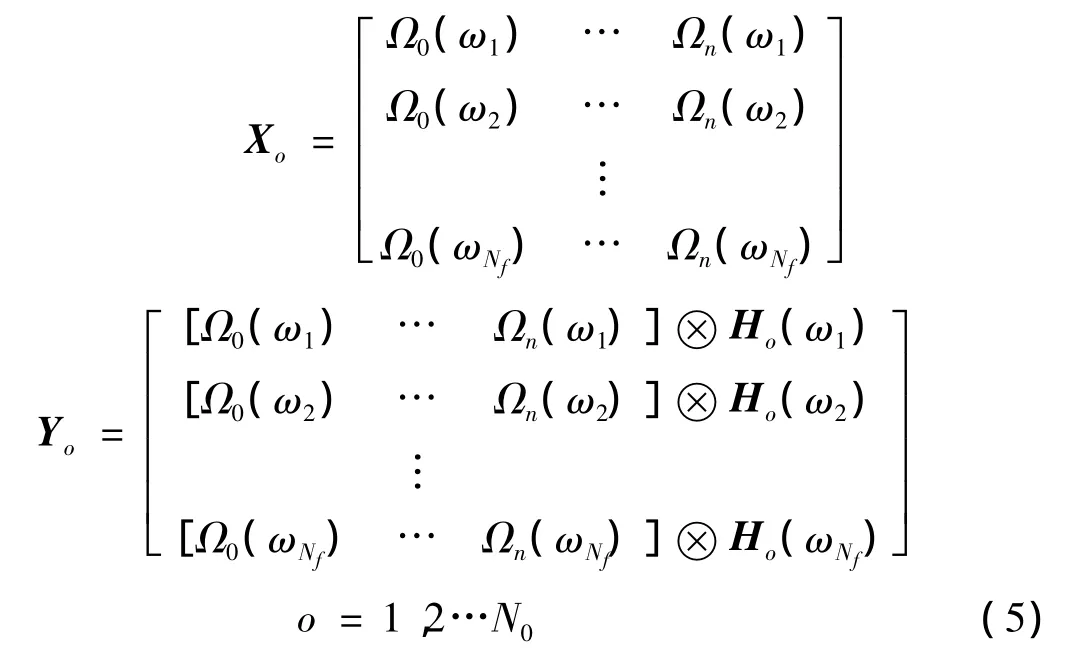
其中⊗为 kronecker积，Nf为识别频段内包含的谱线数。

1.3 通过系数矩阵得到模态参数

当系数矩阵Aj确定之后，模态参数可以通过式(6)中友矩阵进行特征值分解得到:

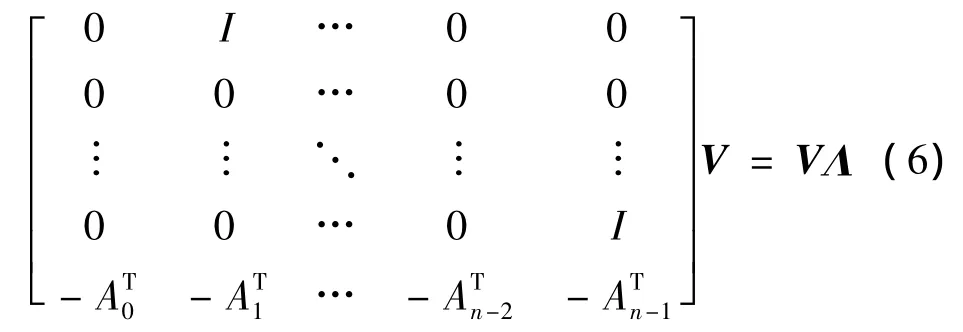
其中极点e－λiTs位于Λ的对角线上，频率与阻尼可以通过式(7)求得，模态参数与向量位于V最后Ni行对应的列向量。

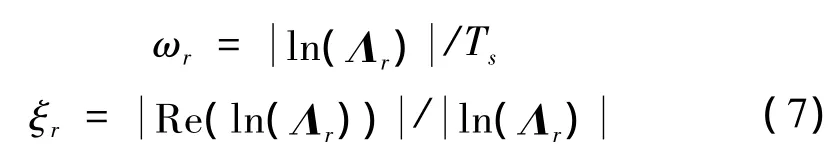
2 PolyMAX算法的快速实现

PolyMAX算法的识别可以按照以下步骤进行:

① 确定出最高计算阶次nmax、最低计算阶次nmin。

② 通过式(4)得到阶次n对应的Ro、So、To。

③ 计算缩减的正则方程M，然后通过最小二乘求解系数矩阵Aj。根据式(6)、式(7)得到模态参数。

④ 改变系统阶次建立稳定图。

在计算 Ro、So、To的过程中，当 Xo、Yo维数很高时，一般不直接通过式(4)中矩阵乘法计算，而是采用FFT 运算代替矩阵乘法［4，5]。当 Ro、So、To计算完成之后，计算量主要集中在正则方程中矩阵M上，因为在建立稳定图的过程中，每一个阶次的改变，都需要重新计算矩阵M，通过式(3)可以看出，这需要大量的矩阵求逆以及矩阵乘法运算。对于复杂结构，输出数目N0很多、计算阶次n很高，在这种情况下计算量尤其突出。

本文通过分析正则方程中矩阵R0的结构，给出其逆矩阵的近似计算方法。从而避免了矩阵的求逆以及乘法运算。通过将基函数表达式 Ω.j(ωk)=exp·(－iωkTs·j)=exp(－i(k－1)/(Nf－1)·j)带入到X0，然后由式(4)得到Ro的表达式如下:

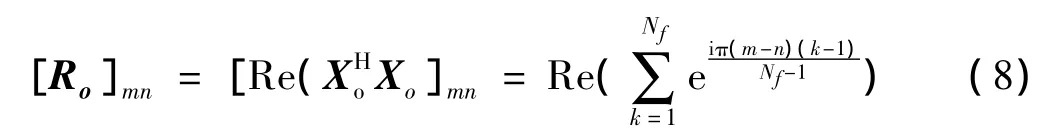
由式(8)可以得出:当 m=n时，［Ro]mn=Nf

当m－n为偶数时:

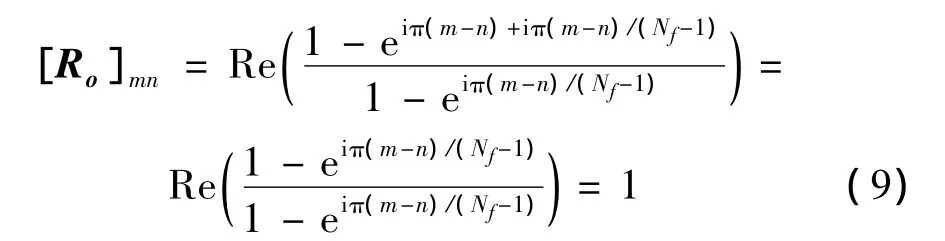
当m－n为奇数时:

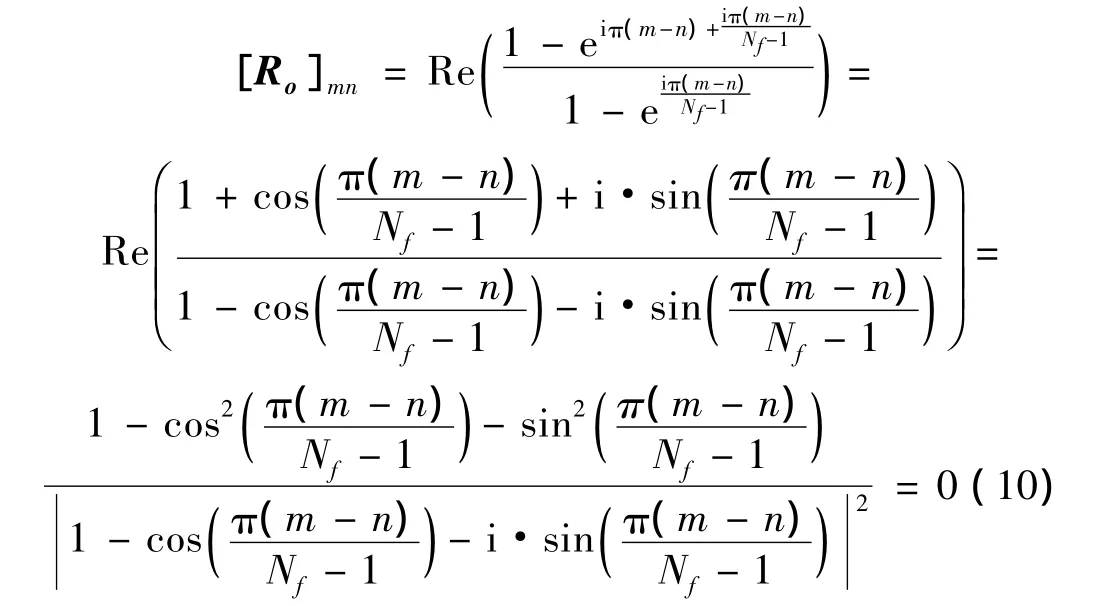
因此Ro具有如下形式:

由于PolyMax为宽频带模态参数识别算法，识别范围内的谱线数Nf≫1，因此:

其中In+1为n+1维的单位矩阵。则M可以写成:

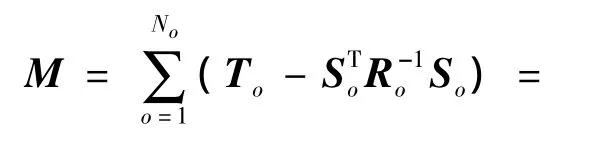
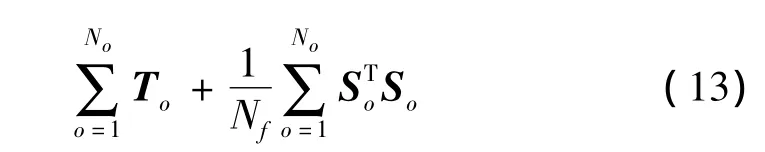
3 仿真算例

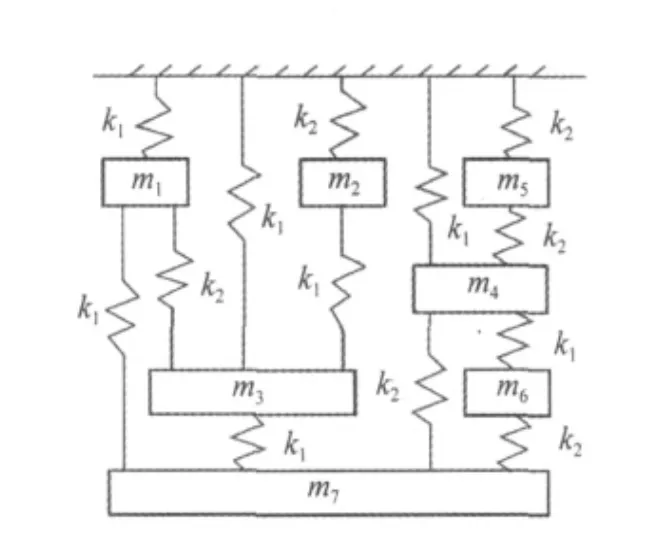
图1 七自由度系统Fig.1 Seven DOF system

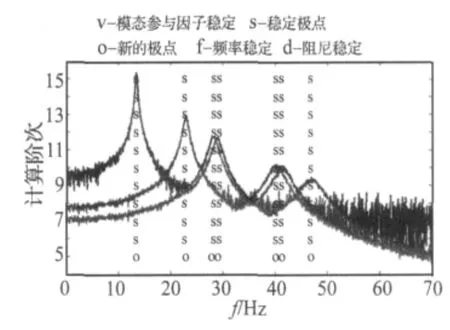
图2 稳定图Fig.2 Stabilization diagram

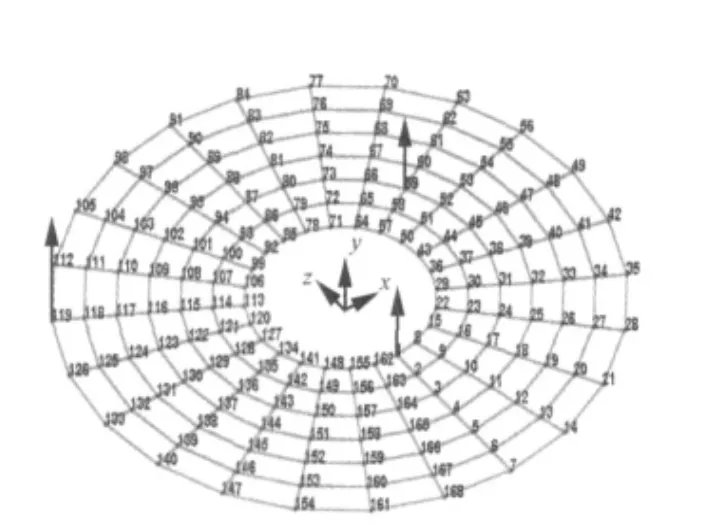
图3 涡轮盘测点布置(箭头为参考点)Fig.3 Measurement setup of gas turbine disk

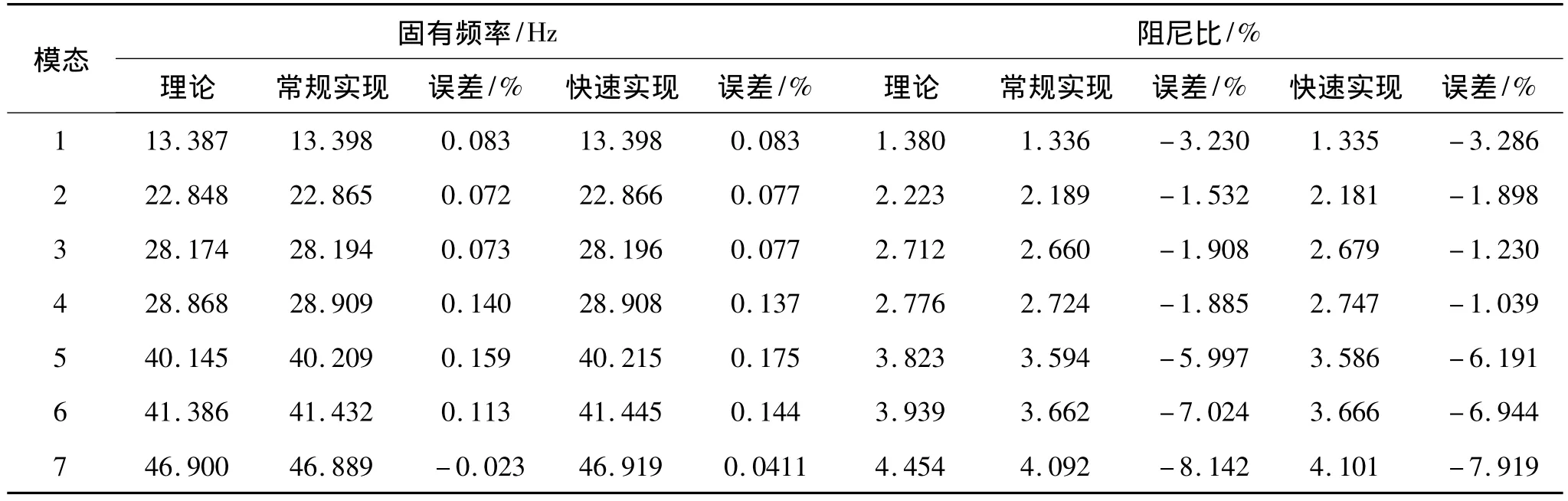
表1 常规实现与快速实现的识别结果比较Tab.1 Identification results between normal and fast implementation

4 实测算例

实测算例来自于某航空发动机涡轮盘模态实验，目的是验证当数据规模比较大时，快速实现方法所能带来的效率提高。实验通过锤击法进行测试，测点布置如图3所示。其中FRF中包含168个输出，3个输入。分析频率范围0－8 000 Hz，谱线数Nf=1 600。在分析范围内大约有50多个结构模态，根据式(14)中模型阶次n与结构模态数目Nm之间的关系，可以得出所需的模型阶次n大约为100阶。

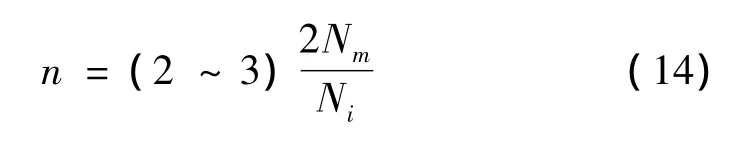
图4为在不同阶次下的计算时间，每一次计算中阶次范围都为20(运行环境为Pentium M 、主频1.6 GHz、1 G内存、Matlab6.5编程)。从图中可以看出在计算阶次不高的情况下，二者的计算时间相差不大。随着计算阶次的提高，快速实现方法所用时间明显少于常规实现方法，并且阶次越高，差距越明显。这说明快速实现方法适合于复杂结构的大规模运算。图5为在最高计算阶次100下得到的稳定图。在此情况下，常规实现所用时间为123.6 s，而快速实现方法所用时间为42.7s。图6为识别的部分振型(前9阶)。

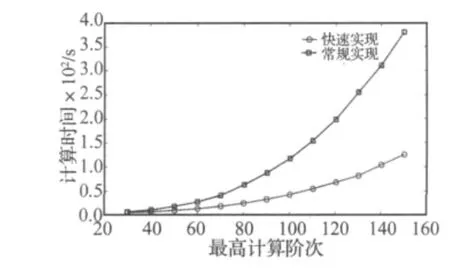
图4 计算时间的比较Fig.4 Comparison of computation time

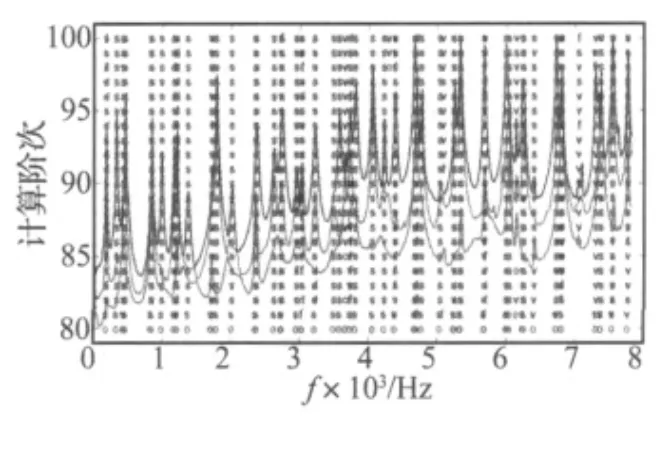
图5 稳定图Fig.5 Stabilization diagram

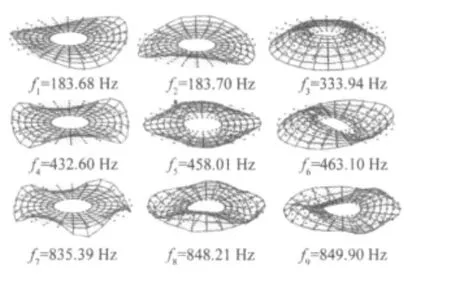
图6 识别的振型Fig.6 Identified modeshapes

5 结论

本文给出了PolyMAX算法的一种快速实现方法，该方法通过避免缩减正则方程中的求逆运算与矩阵乘法，减少了运算量。实测算例表明:在数据量比较大的情况下，与常规实现相比较，采用快速实现后参数识别时间显著减少，证明了该方法的可行性。并且输出数目越多、系统阶次越高的情况效果越明显，因此该方法适合于复杂结构的模态参数识别。

［1] 傅志方，华宏星.模态分析理论与应用［M] .上海:上海交通大学出版社，2000.

［2] Peeters B，Van Der Auweraer H，Guillaume P，et al.The PolyMAX frequency-domain method:a new standard for modal parameter estimation ［J] .Shock and Vibration，2004，11:395－409.

［3] Peeters B，Guillaume P.Automotive and aerospace applictions of the LMS PolyMAX modal parameter estimation method［C] //Proc of the 22th International Modal Analysis Conference，Dearborn，USA，January，2004.

［4] Guillaume P，Verboven P，Vanlanduit S，et al.A polyreference implementation of the least-squares complex frequency domain estimator［C] // Proc of the 21th International Modal Analysis Conference.Kissimmee，USA，February，2003.

［5] Schoukens J，Rolain Y，Gustafsson F，et al.Fast calculation of least-squares for system identification［C] //Proc on the 37th IEEE Conference on Decision ＆ Control，Florida，USA，December，1998，3408 －3410.

［6] Li Z F，Hua H X，Song H W，et al.Extracting modal parameters from structures undergoing ambient excitation excitation［J] .Journal of Shanghai Jiaotong University，2001，2:117－122.

［7] Shih C Y，Tsuei Y G，Allemang R J.Complex mode indication function and its applications to spatial domain parameter estimation［J] .Mechanical System and Signal Processing，1988，2(4):367 －377.