金温线武义江桥列车走行性与行车安全指标研究
周智辉,张 军,秦文孝,曾庆元
(中南大学 土木工程学院,长沙 410075)
对金温线横向振动较大的桥梁进行现场检测,发现部分桥梁横向振幅不同程度地超过《铁路桥梁检定规范》(简称《检规》)规定的行车安全限值。根据《检规》要求,必须采取确保安全的措施,一般是加固桥梁或列车限速过桥。这些桥梁在现行行车条件下已运营多年,桥梁未发现病害现象,列车未见异常的激励,也从未发生安全事故。因此,评估超限桥梁列车走行安全性、平稳性与舒适性,分析《检规》行车安全限值是否能反映桥上列车走行安全性,研究能够反映桥上列车走行安全性的行车安全限值,对充分发挥既有桥梁运能和保证列车安全运行有重大意义。
国内外对铁路桥梁列车走行性与行车安全指标作了大量研究。在分析桥上列车走行性时,大多是计算列车桥梁系统振动响应,根据算出的脱轨系数与轮重减载率指标判别列车是否安全,根据算出的平稳性与舒适性指标判断列车是否平稳舒适[1-5]。前苏联根据机车车辆运营标准,制定了桥梁横向自振周期限值[1]。顾萍等[6]利用大量桥梁横向振幅及对应脱轨系数的实测值与计算值,由脱轨系数Q/P≤0.8的控制标准确定了典型桥梁的横向振幅行车安全限值。曹雪琴等[7]对大量桥墩墩顶横向振幅及横向自振频率的实测值进行统计分析,得出常见桥墩墩顶横向振幅及横向自振频率的通常值。我国2004年颁布的《检规》就是根据上述研究成果分别制定了桥跨结构横向振幅行车安全限值与桥墩墩顶横向振幅及横向自振频率的通常值。李运生等[8]提出了反映桥墩横向振动特性的综合指标,根据桥墩墩顶横向振幅的实测值与理论计算值,由脱轨系数Q/P≤1.0的控制标准确定了提速线轻型桥墩横向刚度检定标准参考限值。已有研究表明脱轨系数和轮重减载率标准对预防脱轨没有控制作用,试验中脱轨系数达到4.98,轮重减载率达到1.0(车轮已悬浮),大大超过标准限值,列车仍然处于安全状态[9,10]。曾庆元等提出列车脱轨能量随机分析理论,依据列车脱轨能量增量判别准则分析了大量桥梁列车走行安全性[11-13]。为此,本文选取金温线武义江32 m预应力混凝土T形梁桥作为研究对象,运用列车脱轨能量随机分析理论,分析了该桥上列车走行安全性、平稳性与舒适性。提出铁路桥梁行车安全指标分析方法,计算了金温线武义江桥横向振幅行车安全限值。
1 列车脱轨能量随机分析理论
曾庆元[11-13]等提出列车脱轨能量随机分析理论,论证了列车脱轨的力学机理是列车-桥梁(轨道)系统横向振动丧失稳定。将分析列车是否脱轨转化为分析列车-桥梁(轨道)系统横向振动是否稳定。基于列车-桥梁(轨道)系统振动能量随机分析理论及系统运动稳定性能量增量判别准则,提出了列车脱轨能量增量判别准则,见式(1)、式(2)、式(3)。

式中:Δσcr与Δσpr分别表示车速为 vr时列车 -桥梁(轨道)系统横向振动极限抗力作功增量与输入能量增量。运用上述理论,对线路上和桥上列车脱轨进行了大量研究,计算了一系列列车是否脱轨实例,计算结果均与实际情况相符,关于该理论的详细内容见文献[11] 。
在应用列车脱轨能量增量判别准则时,考虑到根据理论计算的列车-桥梁(轨道)系统横向振动极限抗力作功增量Δσcr和实测构架蛇形波统计出的列车-桥梁(轨道)系统横向振动输入能量增量Δσpr存在一定误差,作偏安全处理如下。设Δσcr的计算值偏大10%,Δσpr的测试和统计值偏小10%,则得出考虑一定安全度的预防脱轨条件为:

式中:K为安全系数,取为1.23。本文在作桥上列车走行安全性分析时,满足式(4)则认为列车不会脱轨,否则判定列车存在脱轨危险。
2 武义江桥列车走行性分析
2.1 计算模型与计算工况
金温线武义江桥位于金华至温州的江岭-履坦段,中心里程K19+593,其桥跨结构为4×32 m预应力混凝土T形梁(专桥2 059)。下部结构为圆端形实体桥墩(叁桥4 023)与T形桥台(壹桥4 189),墩高20.9 m~24.4 m,墩台基础均为扩大基础。在作桥上列车走行性计算时,选取4跨简支梁墩系统作为桥梁计算对象。现场实测与理论计算均证明:全列空载及空重混编货物列车过桥时,列车-桥梁(轨道)系统振动响应最大,空载货车发生脱轨的概率最大[14]。因此,在作货物列车走行安全性、平稳性及舒适性计算时,选空载货物列车为最不利的行车工况,取DF4机车牵引25辆C62空载货车作为货物列车计算对象。另外,选取DF11机车牵引14辆客车作为旅客列车计算对象。根据金温线现行行车条件,货物列车计算车速为60 km/h~70 km/h,旅客列车计算车速为70 km/h~90 km/h。分别建立列车、桥梁的有限元模型,钢轨位移由对应处桥梁位移表述,考虑轮轨衔接条件与轮轨“游间”的影响,建立列车-梁墩系统空间振动计算模型。该计算模型可用于计算桥上列车是否脱轨与正常条件下列车-梁墩系统振动响应,关于计算模型的详细内容见文献[1,11] 。
2.2 桥上列车走行性分析
运用列车脱轨能量随机分析理论,计算武义江桥上货物列车与旅客列车走行安全性,计算结果见表1。计算结果表明:货物列车以不超过70 km/h速度过桥,旅客列车以不超过90 km/h速度过桥,列车-梁墩系统横向振动是稳定的,货物列车与旅客列车均不会脱轨。
基于列车-梁墩系统空间振动计算模型,计算列车-梁墩系统在正常行车条件下的最大振动响应及列车最大平稳性(对货车)和舒适性(对机车与客车)指标,计算结果见表2。根据我国铁道机车车辆动力学性能评定标准,由计算结果可知,货物列车以70 km/h及以下车速过桥时,机车Sperling指标不超过3.45,货车Sperling指标不超过4.25,均满足合格要求;旅客列车以90 km/h及以下速度过桥时,机车在90 km/h车速时横向Sperling指标低于3.45,满足合格标准,其余均低于3.10,达到良好标准,客车Sperling指标低于2.75,达到了良好标准。可见,在金温线现行行车条件下,武义江桥上货物列车与旅客列车的平稳性和舒适性能够得到保证。
货物列车过桥时,桥梁跨中计算最大横向振幅为4.13 mm(对应的货车计算车速为70 km/h),实测最大横向振幅为4.33 mm(对应的货车试验车速为77.7 km/h),均超过了《检规》行车安全限值(该桥对应的行车安全限值为3.56 mm)。理论计算表明列车的走行安全性、平稳性与舒适性均可以保证。建议对该桥不采取限速或加固措施,该建议已被金温铁路公司采纳。在现行行车条件下,武义江桥计算横向振幅超过其行车安全限值16%。从理论计算结果与武义江桥多年行车情况可知,桥梁跨中横向振幅超过《检规》行车安全限值一定幅度,列车不一定就存在脱轨危险。此外,文献[11] 中分析了6座横向振幅超限桥梁的列车走行安全性,计算结果同样表明:尽管横向振幅存在不同程度的超限现象,但列车安全性可以保证。可见,根据现有《检规》行车安全限值判别桥上列车是否安全并确定是否对桥梁采取加固或限速措施,会造成不必要加固投资或制约既有铁路桥梁运能的发挥。因此,研究反映列车走行安全性的桥梁行车安全指标十分必要。
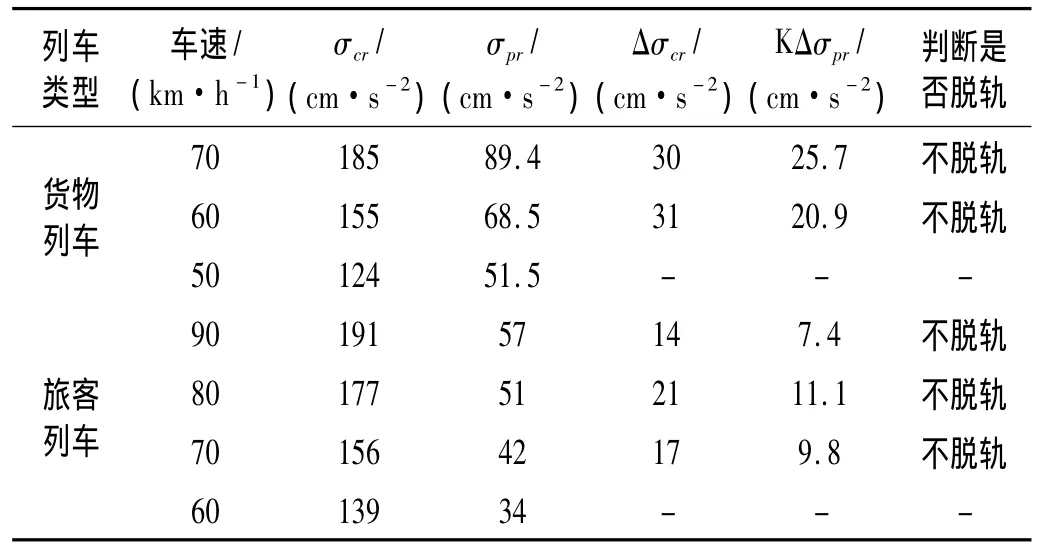
表1 武义江桥列车走行安全性计算结果Tab.1 Calculated results of running safety of train onWuyiriver bridge
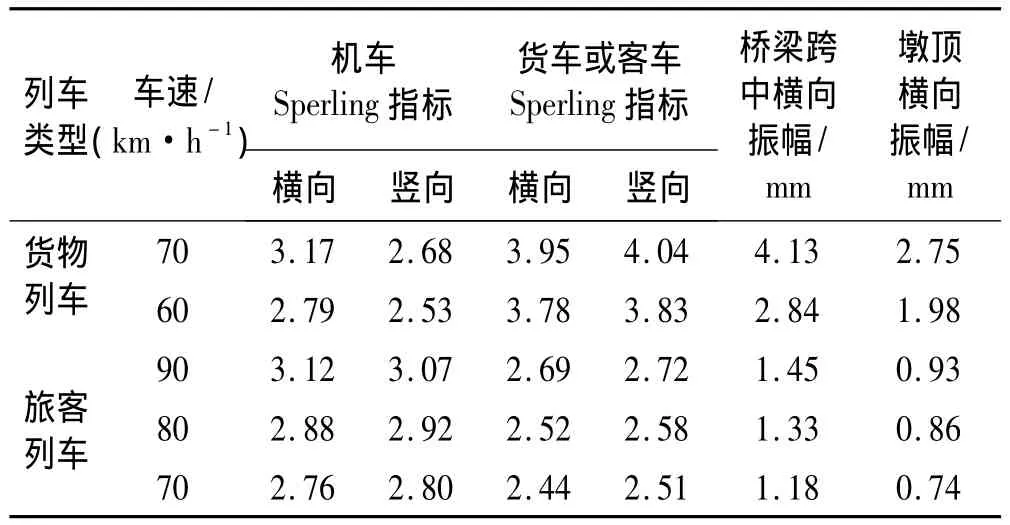
表2 武义江桥列车走行平稳性与舒适性计算结果Tab.2 Calculated results of running smoothness and comfort of train on Wuyi river bridge
3 铁路桥梁行车安全指标分析方法
3.1 确定梁墩系统行车安全判别参数
在行车条件一定的情况下,桥梁横向刚度是影响桥上列车走行安全性的主要因素[15]。研究桥梁横向动力性能,应将桥跨结构与桥墩组成的整体系统作为研究对象。针对确定的桥跨结构,选择与之匹配的桥墩横向刚度,使梁墩系统具有足够的横向刚度,以保证桥上列车安全、平稳及舒适运行。京山线老滦河桥上行线桥梁横向刚度大于下行线桥梁。上行线桥梁上从未发生列车脱轨,而下行线桥梁上曾连续三次发生货物列车脱轨事故。该桥下行线桥梁实测跨中横向振幅比上行线桥梁跨中横向振幅大很多[15]。可见,桥梁跨中横向振幅综合反映了梁墩系统横向刚度性能。因此,确定桥梁跨中横向振幅作为梁墩系统行车安全判别参数。满足桥上列车安全、平稳及舒适运行要求的桥梁跨中最大横向振幅即为桥梁横向振幅行车安全限值。
3.2 确定保证列车安全、平稳及舒适运行的临界梁墩系统
建立列车-梁墩系统空间振动计算模型,运用列车脱轨能量随机分析理论,计算不同横向刚度的梁墩系统(不同横向刚度的桥墩与给定桥跨结构组成不同横向刚度的梁墩系统)的列车走行安全性。随着桥墩高度逐步增加,桥墩与梁墩系统的横向刚度逐步减弱,梁墩系统抵抗列车脱轨的能力逐步降低。当梁墩系统横向刚度降到一定程度,预防脱轨条件式(4)不能满足,而上一步计算所对应的梁墩系统的横向刚度,满足预防脱轨条件式(4)。称上一步计算对应的梁墩系统为预防脱轨的临界梁墩系统,相应墩高为预防脱轨的临界墩高。
预防脱轨的临界梁墩系统能保证列车不会脱轨。在此条件下,计算预防脱轨的临界梁墩系统的车桥系统振动响应,作列车走行平稳性与舒适性分析。如果所计算的梁墩系统不能保证列车平稳、舒适过桥,那么逐步减少桥墩高度,增大梁墩系统横向刚度,继续计算其列车走行平稳性与舒适性,直到找到能保证列车安全、平稳及舒适运行的临界梁墩系统(简称临界梁墩系统)为止,对应的墩高称为保证列车安全、平稳及舒适运行的临界墩高(简称临界墩高)。
3.3 确定梁墩系统跨中横向振幅行车安全限值
根据车桥系统振动响应计算,得到正常条件下临界梁墩系统桥梁跨中横向振幅。当桥墩高度低于临界墩高时,桥梁横向刚度高于临界梁墩系统的横向刚度,列车走行安全性、平稳性与舒适性有保障,相应桥梁跨中横向振幅小于临界梁墩系统的跨中横向振幅。当桥墩高度高于临界墩高时,桥梁横向刚度低于临界梁墩系统的横向刚度,列车走行安全性、平稳性与舒适性不能保障,相应桥梁跨中横向振幅大于临界梁墩系统的跨中横向振幅。故取临界梁墩系统跨中横向振幅作为桥梁横向振幅行车安全限值。
4 武义江桥行车安全指标分析
以武义江桥32 m预应力混凝土T形梁桥为基础,保持桥跨结构不变,桥墩型号不变,桥墩高度由既有桥桥墩高度24.4 m按1 m的幅度逐步增加,从而逐步减小桥墩横向刚度,降低梁墩系统横向刚度,寻找预防脱轨的临界梁墩系统。分别计算不同横向刚度的梁墩系统列车走行安全性,所采用的计算列车及计算车速同该桥列车走行性分析部分。墩高为24.4 m(既有武义江桥墩高)、28.4 m及29.4 m时,相应的计算结果列于表3与表4。计算结果表明:当桥墩高度增到29.4 m时,速度为70 km/h的货物列车过桥时,不满足预防脱轨条件式(4),有脱轨危险。当墩高为28.4 m时,货物列车以车速70 km/h过桥,满足预防脱轨条件式(4),不会脱轨。桥墩高度为24.4 m~29.4 m,旅客列车过桥时,均满足预防脱轨条件式(4),不会脱轨。因此,墩高28.4 m为武义江桥预防脱轨的临界墩高,28.4 m高的桥墩与桥跨结构组成的梁墩系统为预防脱轨的临界梁墩系统。
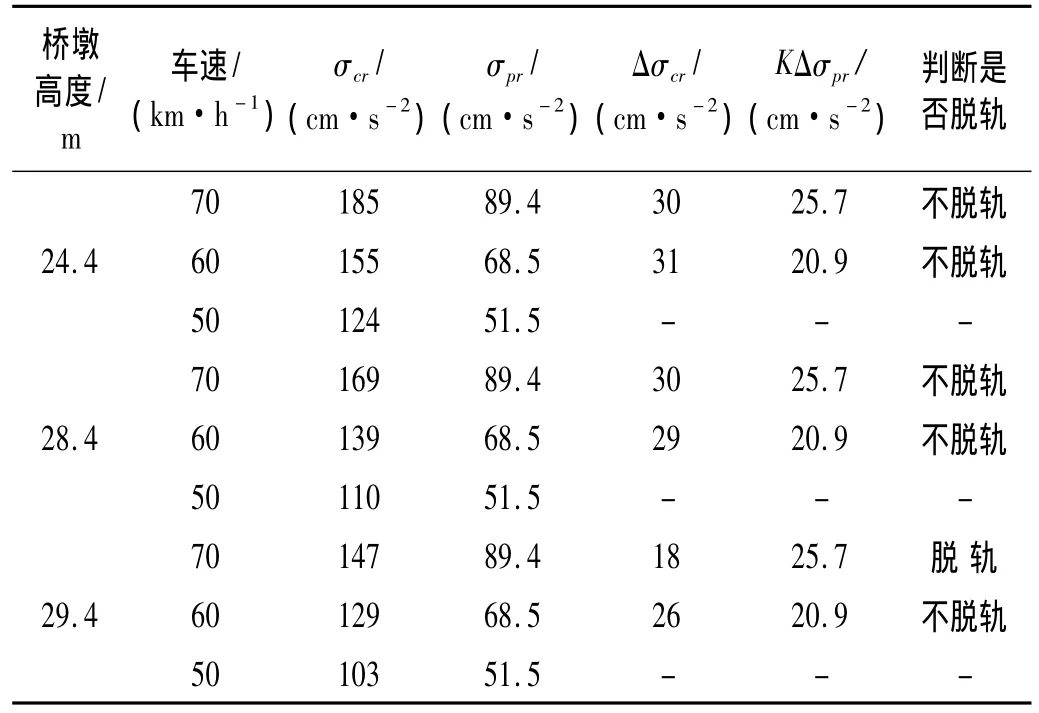
表3 不同墩高的梁墩系统货物列车走行安全性计算结果Tab.3 Calculated results of running safety of freight train on beam-pier system with different pier height
同样,计算不同梁墩系统列车走行平稳性与舒适性以及相应的桥梁振动响应。墩高为24.4 m、27.4 m及28.4 m时,相应的计算结果列于表5与表6。计算结果表明:当墩高为预防脱轨的临界墩高(28.4 m),货物列车车速为70 km/h时,货车 Sperling指标超过4.25,不满足合格要求。当墩高为27.4 m,货物列车车速在70 km/h及以下时,机车Sperling指标小于3.45,货车Sperling指标小于4.25,均满足合格要求。而在桥墩高度为24.4 m~28.4 m时,旅客列车以90 km/h及以下车速过桥,机车Sperling指标小于3.45,客车Sperling指标小于3.0,均满足合格要求。因此,墩高27.4 m为武义江桥的临界墩高,27.4 m高的桥墩与桥跨结构组成的梁墩系统为临界梁墩系统。
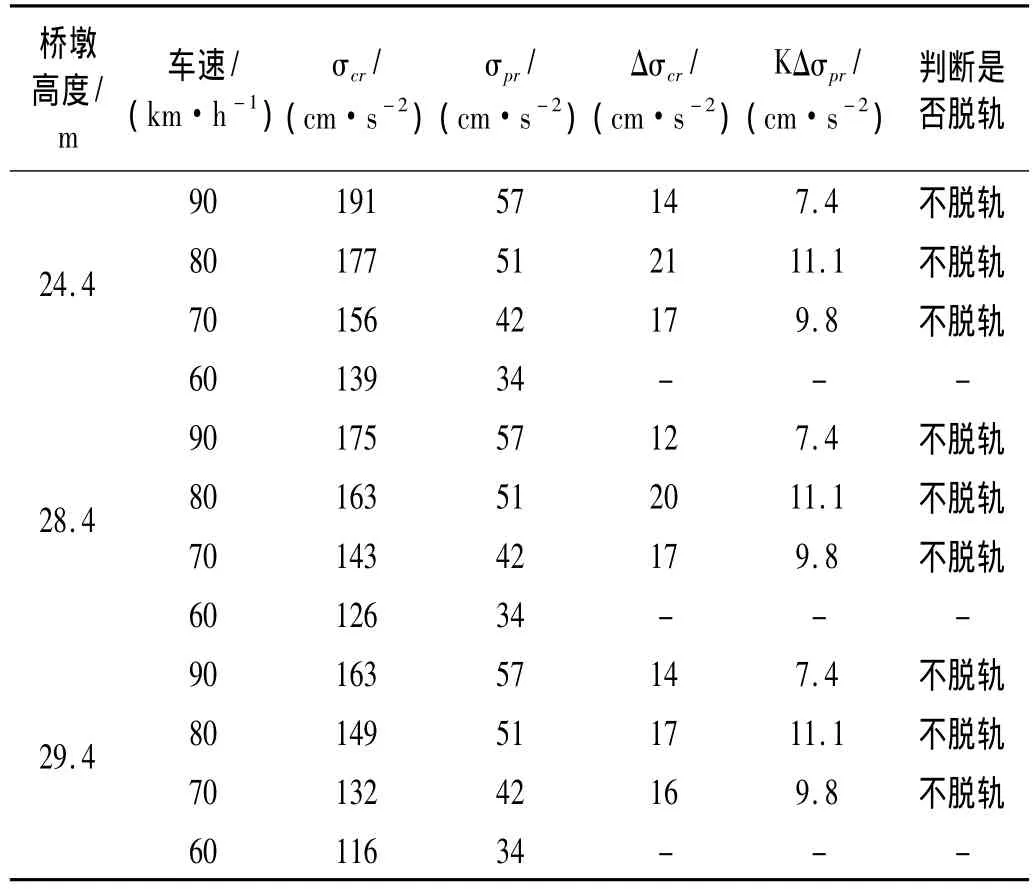
表4 不同墩高的梁墩系统旅客列车走行安全性计算结果Tab.4 Calculated results of running safety of passenger train on beam-pier system with different pier height
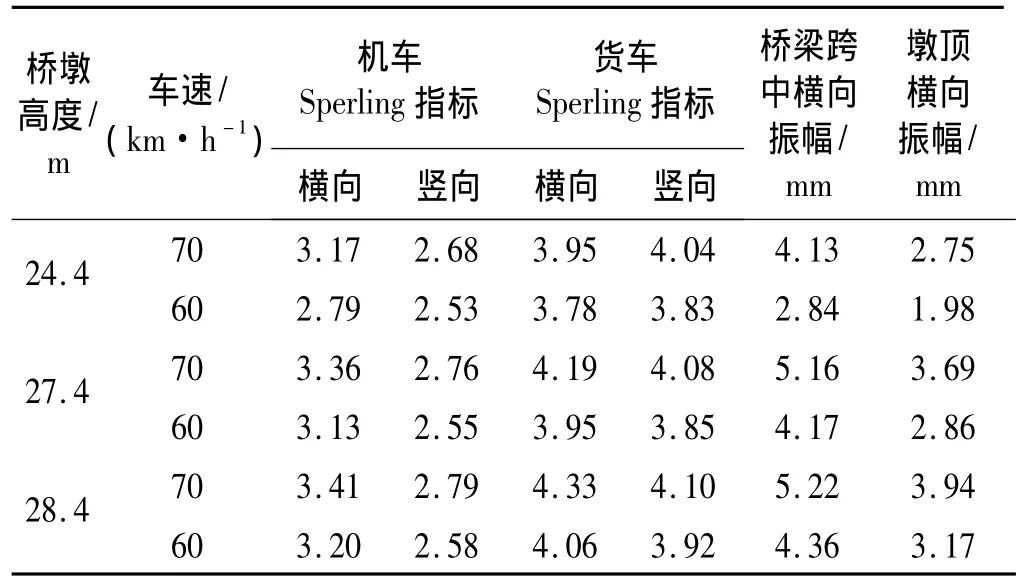
表5 不同墩高的梁墩系统货物列车走行平稳性及舒适性计算结果Tab.5 Calculated results of running smoothness and comfort of freight train on beam-pier system with different pier height
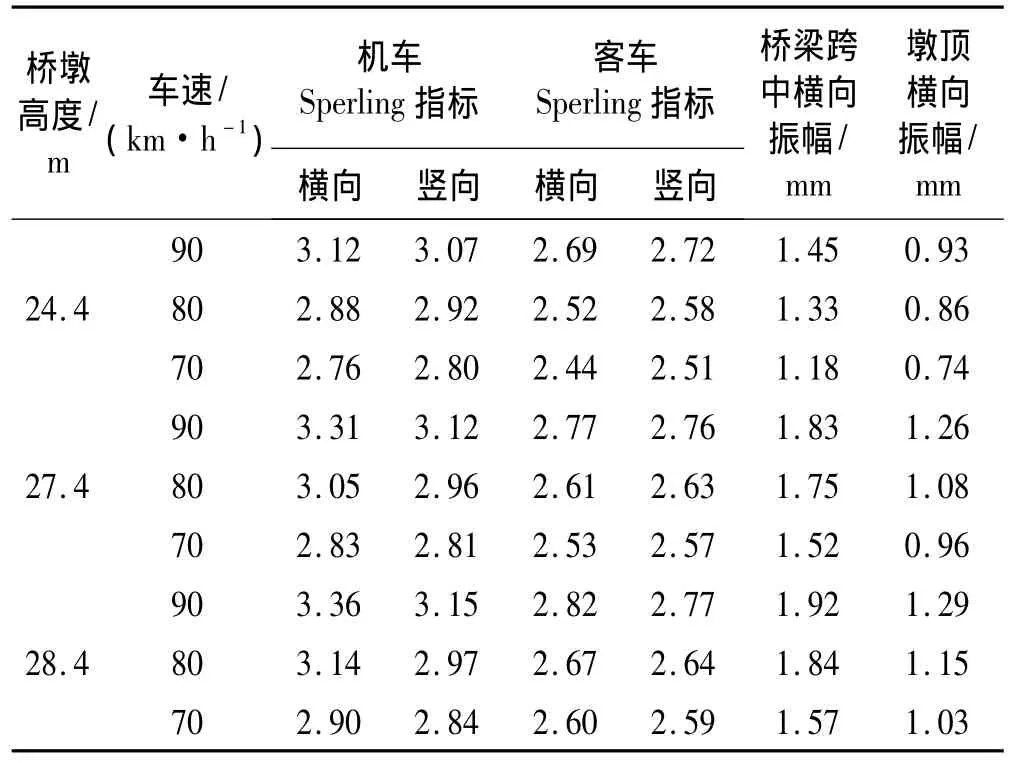
表6 不同墩高的梁墩系统旅客列车走行舒适性计算结果Tab.6 Calculated results of running comfort of passenger train on beam-pier system with different pier height
武义江桥临界梁墩系统跨中横向振幅计算值为5.16 mm。当桥梁横向刚度高于临界梁墩系统横向刚度时,桥梁跨中横向振幅小于5.16 mm,列车走行安全性、平稳性与舒适性有保障。当桥梁横向刚度低于临界梁墩系统横向刚度时,桥梁跨中横向振幅大于5.16 mm,列车走行安全性、平稳性与舒适性不能保证。因此,武义江32 m预应力混凝土T形梁桥横向振幅行车安全限值可取为5.16 mm,约为L/6 200,其中跨度L单位取为mm。
本文计算的武义江32 m预应力混凝土T形梁桥的横向振幅行车安全限值为5.16 mm,比现有《检规》行车安全限值3.56 mm大45%。可见,现有《检规》行车安全限值可以适当放宽,这样有利于发挥既有桥梁的运能,节省大量的加固费用。本文是“金温铁路桥梁列车脱轨分析与行车安全指标研究”的部分成果,该成果已通过了上海铁路局的鉴定,并在金温铁路得到了应用。尽管本文限值L/6200仅根据武义江桥分析结果得出,对普速铁路预应力混凝土简支梁桥行车安全限值同样有参考价值。要得到预应力混凝土简支梁桥有代表性的行车安全限值,必须研究更多的桥梁类型与行车工况,总结归纳出此类桥梁的行车安全限值。本文旨在分析《检规》存在的问题,并提出铁路桥梁行车安全指标分析方法。
5 结论
(1)运用列车脱轨能量随机分析理论计算了金温线武义江桥列车走行性。计算结果表明尽管该桥横向振幅超过《检规》行车安全限值,但列车走行安全性、平稳性与舒适性有保障。建议对该桥不采取限速或加固措施。
(2)基于列车脱轨能量随机分析理论,提出铁路桥梁行车安全指标分析方法。确定桥梁跨中横向振幅作为梁墩系统行车安全判别参数,计算找出保证列车安全、平稳及舒适运行的临界梁墩系统,计算出临界梁墩系统跨中横向振幅作为桥梁行车安全限值。
(3)计算出金温线武义江32 m预应力混凝土T形梁桥横向振幅行车安全限值为L/6 200。新限值既充分发挥桥梁的运能,又确保了列车安全运行。
[1] 曾庆元,郭向荣.列车桥梁时变系统振动分析理论与应用[M] .北京:中国铁道出版社,1999.
[2] Yang Y B,Wu Y S.A versatile element for analyzing vehicle-bridge interaction response[J] . Engineering Structures,2001,23(1):452 -469.
[3] 夏 禾.车辆与结构动力相互作用[M] .北京:科学出版社,2002.
[4] 李小珍,强士中.大跨度公铁两用斜拉桥车桥动力分析[J] .振动与冲击,2003,22(1):6 -9,19,25.
[5] 高芒芒,李永强,许兆军,等.高速列车作用下的芜湖长江大桥车桥耦合振动分析[J] .中国铁道科学,2001,22(5):34-40.
[6] 顾 萍.根据货车脱轨安全度确定铁路钢桥的横向振幅限值[J] .铁道学报,2000,22(增刊):87 -91.
[7] 曹雪琴,吴定俊,罗蔚文,等.铁路桥梁刚度检定标准总报告[R] .上海:上海铁道大学,1998.
[8] 李运生.铁路桥墩横向振动理论和试验研究[D] .北京:北京交通大学土木建筑工程学院,2005.
[9] 铁道部科学研究院,北京铁路局.大秦线C63A货物列车脱轨试验报告[R] .北京:铁道部科学研究院,1997.
[10] 翟婉明.车辆-轨道耦合动力学[M] .北京:中国铁道出版社,2002.
[11] 曾庆元,向 俊,周智辉,等.列车脱轨分析理论与应用[M] .长沙:中南大学出版社,2006.
[12] 曾庆元,向 俊,娄 平.车桥及车轨时变系统横向计算中的根本问题与列车脱轨能量随机分析理论[J] .中国铁道科学,2002,23(1):1-10.
[13] 周智辉,曾庆元.桥上列车脱轨计算分析[J] .中国铁道科学,2004,25(4):46 -49.
[14] 向 俊,孔凡兵,曾庆元.货物列车编组对列车-桥梁系统空间振动的影响[J] .中南大学学报:自然科学版,2007,38(2):345 -350.
[15] 周智辉,曾庆元,向 俊.桥梁横向刚度对列车走行安全性的影响[J] .铁道科学与工程学报,2005,2(2):30 -33.

