主轴系统结合面对主轴系统动力学特性的影响分析

汪 博， 孙 伟， 太兴宇， 闻邦椿

(东北大学 机械工程与自动化学院，沈阳 110004)

主轴系统是数控机床的核心部件之一，其动力学特性直接影响数控机床的加工精度、表面粗糙度和工作效率。因而围绕主轴系统动力学特性的设计与分析受到了企业界及学术界的广泛关注［1]。

以高档立式加工中心为例，其主轴系统通常包括主轴箱、电主轴、轴承、刀柄、刀具等。主轴系统中存在着主轴－轴承、主轴－刀柄、刀柄－刀具结合面，而这些结合面对主轴系统动力学特性有着显著的影响。目前，学者们围绕主轴系统结合面建模、测试以及考虑结合面的振动特性分析，做了大量的工作，且取得了很多成果。例如:文献［2] 介绍了Li所建立的主轴－轴承系统动力学模型，该模型包含了一个综合的轴承动态模型、一个主轴动态模型和一个热模型，能很好地计算轴承的热膨胀及其引起的动态特性。文献［3] 基于Hertz接触力模型，将主轴－滚动轴承系统简化为六自由度系统，讨论在非平衡力作用下，主轴－轴承系统的非线性动态特性。文献［4] 采用Jones’轴承模型对主轴轴承进行了建模与分析，利用有限元法对主轴系统进行了动力学建模，通过此模型可以预测轴承刚度、模态振型、频响函数以及主轴各部分的动力学响应。文献［5] 利用弹性阻抗耦合理论建立主轴－刀柄－刀具系统的运动方程，通过测试刀尖点频响函数，反推出主轴－刀柄、刀柄－刀具结合面的复刚度矩阵，辨识出了结合面的动力学参数。

从以上研究可以看出，主轴系统结合面对主轴系统动力学特性有着显著的影响，这已经得到公认。但是这些结合面对主轴系统动力学特性究竟有何影响还未得到确认。而获得这个影响规律，对于主轴系统动力学设计与性能预估都有着重要的意义。

本文主要采用有限元方法分析主轴系统各结合面对主轴系统动力学特性的影响规律。以某立式加工中心主轴系统为对象，详细描述了利用有限元法对其进行动力学建模的过程。在此基础上，采用对比分析，研究了结合面特性对该主轴系统固有特性和刀尖点频响函数的影响规律。本文研究也可为主轴系统动力学特性及稳定性预估提供参考。

1 主轴系统有限元建模

对主轴系统有限元建模，按选取单元的不同，可以分为两种方法，分别是采用实体单元的建模法和采用简化单元(例如梁单元和管单元)的建模方法。实体模型建模法，便于考虑主轴结合面的空间分布特性，得到了广泛应用，例如文献［6] 。而简化模型具有分析方便、运算快捷，而且还可以考虑复杂的剪切效应，同样也是重要的分析手段。这里考虑分析的方便性，利用简化模型对某立式加工中心主轴系统进行有限元建模。

1.1 主轴有限元建模

某立式加工中心主轴系统如图1所示。采用简化模型法时，可将主轴系统划分成若干轴段，并假设主轴系统的质量是均匀的。主轴系统几何尺寸见表1所示。假设主轴、刀柄、刀具为同一材料，具体的材料参数为:杨氏模量 E=2.06 ×1011N/m，泊松比 μ =0.3，密度 ρ=7 800 kg/m3。

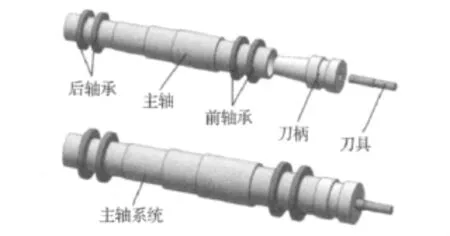
图1 某立式加工中心主轴系统Fig.1 The spindle system of vertical machining center

本文利用ANSYS软件进行主轴系统的有限元建模，选用Pipe16管单元。Pipe16管单元是基于三维梁单元，根据对称性和标准管几何尺寸进行简化，具有拉压、扭转和弯曲性能，该单元在每个节点有6个自由度，沿节点X，Y，Z方向的平移和绕节点X，Y，Z轴的旋转。同时赋予这些单元截面实常数，模拟主轴、刀柄、刀具各轴段的动力学特性及结构。

当刀柄插入主轴、刀具插入刀柄时，假设刀柄和刀具与主轴和刀柄结合的部分分别与主轴和刀柄刚性地连接在一起，构成修正后的主轴系统。主轴、刀柄、刀具的尺寸也因此而改变。

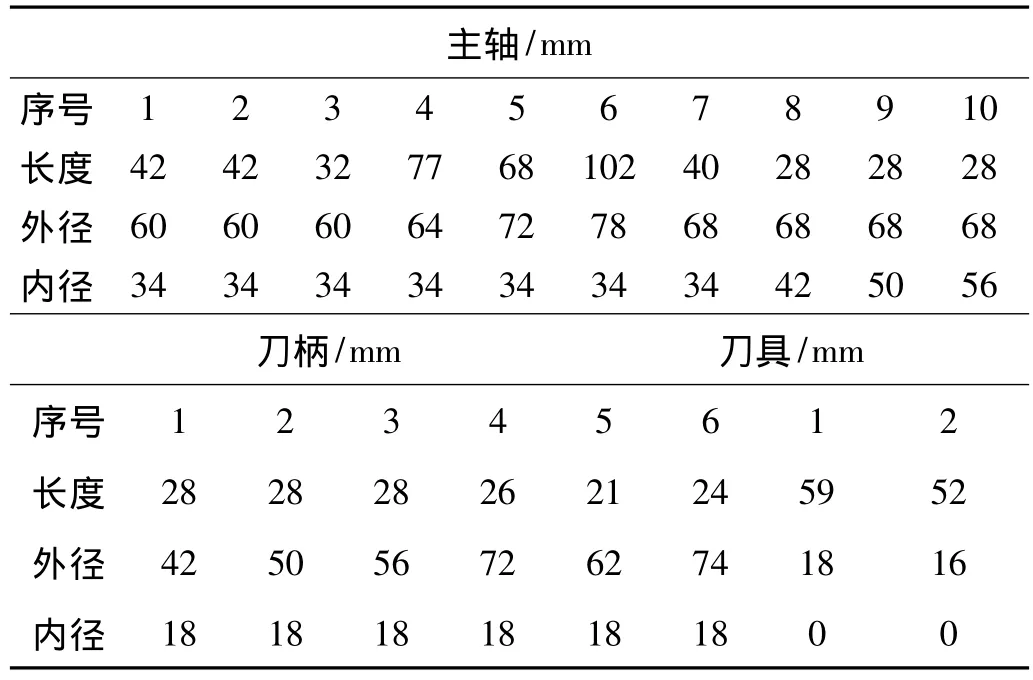
表1 主轴系统几何参数Tab.1 Geometrical parameter of spindle system

1.2 主轴系统结合面建模

在建立主轴、刀柄和刀具模型的同时，也要考虑对主轴－轴承、主轴 －刀柄、刀柄 －刀具结合面进行处理。

对于电主轴的角接触轴承，将其简化为弹性支承;假设轴承平动刚度为定值，不随轴承负载和转速而变化，转动刚度为零。该主轴前后各两个轴承支承的空间位置分布见表2。

表2 轴承在主轴系统中的空间位置分布Tab.2 Distribution of the bearing on spindle system

针对主轴－刀柄、刀柄－刀具结合面，用弹簧阻尼单元来模拟修正后的主轴－刀柄、刀柄－刀具结合面动态特性(包括平动和转动)。对照同类主轴系统确定上述结合面的刚度，如表3所示。

表3 主轴系统结合面刚度Tab.3 Dynamical properties of the bearings and interfaces

选用MATRIX27单元模拟主轴系统结合面(轴承、主轴－刀柄、刀柄－刀具)的平动刚度和转动刚度。MATRIX27单元连接2个节点，每个节点有6个自由度，该单元是12×12的矩阵，可表示为:

模拟结合面动力学特性时，只需将矩阵中对应元素赋以相应的值，以主轴－刀柄结合面为例，其在Y，Z方向有平动刚度，在绕Y，Z旋转方向有转动刚度，输入实常数分别为:C13=C64=6×107，C19= －6×107，C24=C69=6 ×107，C30= －6 ×107，C43=C76=2 ×106，C49= －2 ×106，C51=C78=2 ×106，C57= －2×106。

综上，经过简化处理的主轴系统，利用ANSYS软件完成建模，共划分91个单元，92个节点，如图2所示，其中刀尖节点编号为88。

图2 主轴系统有限元模型Fig.2 The finite element model of spindle system

2 主轴系统结合面对主轴系统固有特性的影响

目前对主轴系统固有特性的研究时，大多只考虑轴承结合面，而忽略了主轴－刀柄、刀柄－刀具结合面的影响，但在实际的机床主轴系统中，主轴－刀柄、刀柄－刀具结合面对主轴系统动力学特性的影响是客观存在的。这里对比分析了仅考虑轴承结合面及考虑全部结合面对主轴系统固有特性的影响。

2.1 结合面对主轴系统固有特性的影响

在仅考虑主轴－轴承结合面情况下，假设主轴－刀柄、刀柄－刀具之间是刚性连接;而考虑全部结合面时，将主轴－刀柄、刀柄－刀具结合面的平动刚度和转动刚度引入到系统模型中。将两种情况下前8阶固有频率列于表4;对应的仅考虑主轴－轴承结合面时的前四阶振型见图3;考虑全部结合面的前四阶振型见图4，其中前两阶为刚体振型，后两阶为弹性体振型。

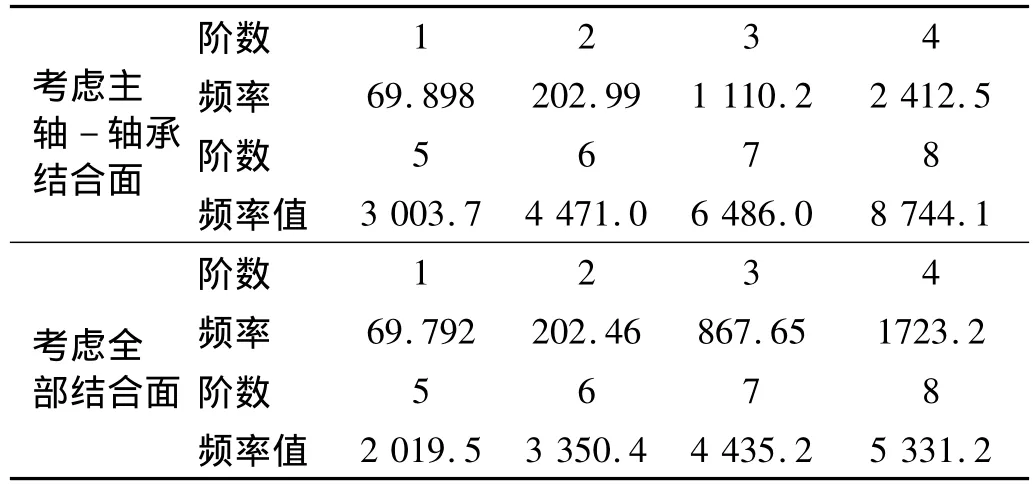
表4 两种情况下主轴系统前8阶固有频率(Hz)Tab.4 The first eight order inherent frequencies under two different situations(Hz)

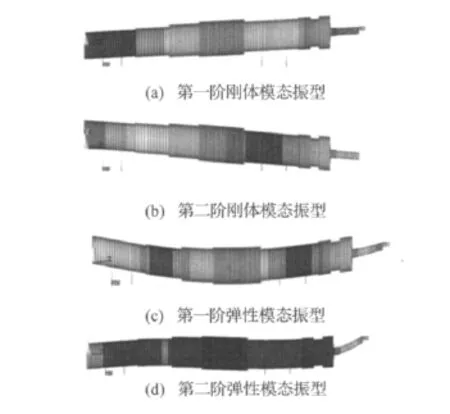
图3 仅考虑主轴－轴承结合面时主轴系统模态振型Fig.3 The modal shape of spindle system with only spindle-bearing interface

2.2 影响分析

通过对比固有频率值及振型可以看出:

(1)主轴－轴承结合面动力学特性仅影响主轴系统刚体模态，不影响弹性模态;

(2)主轴－刀柄、刀柄－刀具结合面对主轴系统的弹性模态影响较为明显;

图4 考虑全部结合面时主轴系统弹性模态振型Fig.4 The modal shape of spindle system with all interfaces

(3)主轴系统中考虑全部结合面的动力学特性(包括平动刚度和转动刚度)之后，主轴系统弹性模态的固有频率值明显降低。

3 主轴系统结合面对主轴系统频响函数的影响

3.1 刀尖点频响函数的含义

主轴系统刀尖点频响函数是指在一定的频率范围内对主轴系统刀尖点激励，同时在刀尖点识振，通过两者的比值获得的频响函数，又可以称之为刀尖点的原点频响或直接频响，其表达式对应着频响函数矩阵中的一个元素，可以表示为

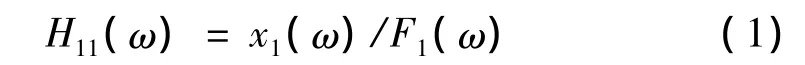
由主轴系统刀尖点频响函数可以得出系统的固有频率、动刚度(频响函数的倒数)以及对主轴系统稳定性做出评价，因而，获得主轴系统刀尖点频响函数有着重要的意义。

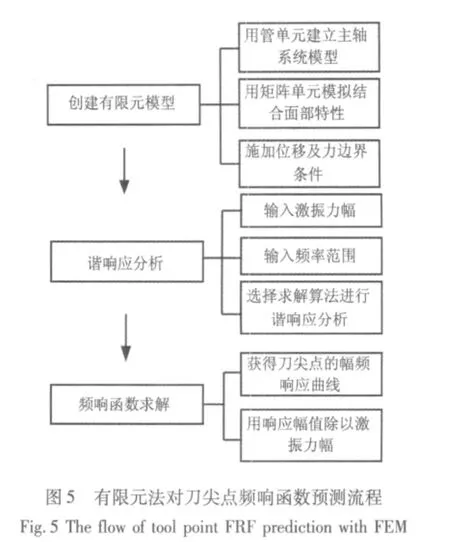
用有限元法来求解主轴系统刀尖点的频响函数的具体思想是:通过谐响应分析获得刀尖点在指定力幅的正弦扫频激励下的谐响应，用谐响应幅值除以力幅即可获得刀尖点的频响函数。刀尖点频响函数预测流程如图5所示。

3.2 结合面对主轴系统频响函数的影响

同样按两种情况，即仅考虑主轴－轴承结合面和考虑全部结合面，用图5所示的流程预测刀尖点的频响函数。

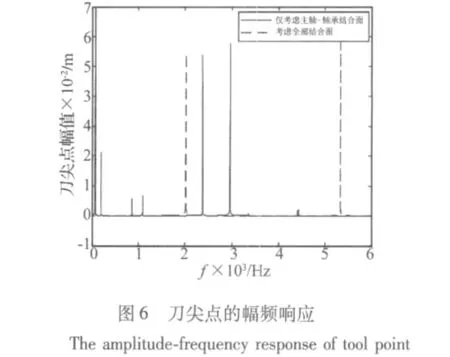
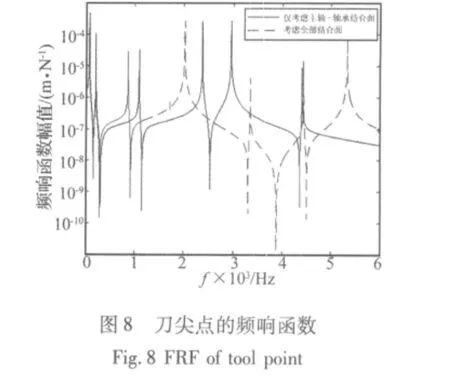
在刀尖点径向(节点号88)施加大小为200 N，频率范围为1 Hz至6 000 Hz的谐波载荷，选用模态叠加法求解主轴系统的谐响应。得到两种情况下刀尖点在频率1至6 000范围内的幅频响应X，见图6。利用频响函数的定义式，这里的激励可以用图7来描述，接着用获得的幅频响应X除以激振力F，就可以获得刀尖点的频响函数，见图8。

3.3 影响分析

从主轴系统刀尖点的幅频响应图(图6)和刀尖点频响函数图(图8)中可以看出:

(1)主轴系统刀尖点在低频段(前2阶，即主轴系统刚体模态所对应的频率段为低频段)的频响函数主要受到主轴－轴承结合面动力学特性的影响;

(2)主轴系统刀尖点在高频段(高于2阶，即主轴系统弹性模态所对应的频率段为高频段)的频响函数主要受到主轴－刀柄、刀柄－刀具结合面动力学特性的影响，而主轴－轴承结合部对高频段的影响很小。

4 结论

主轴系统结合面是影响主轴系统动力学特性的关键因素，分析结合面对主轴系统动力学特性的影响，对研究主轴系统动力学特性、优化主轴系统抗振性能具有重要意义。本文采用有限元法对主轴系统进行建模，分析了结合面对主轴系统动力学特性的影响，主要工作包括:

(1)考虑主轴系统结合面动力学特性，采用有限元分析方法，应用Pipe16管单元和MATRIX27矩阵单元创建了主轴系统的有限元模型。

(2)通过对主轴系统固有特性分析，得出主轴－轴承结合面影响主轴系统刚体模态;而主轴－刀柄、刀柄－刀具结合面影响主轴系统的弹性模态;考虑主轴系统全部结合面动力学特性之后，主轴系统弹性模态固有频率有明显降低。

(3)提出了基于有限元法的主轴系统刀尖点频响函数分析流程。通过对主轴系统频响函数的分析，得出主轴－轴承结合面影响刀尖点的低频段的频响函数;而主轴－刀柄、刀柄－刀具结合面主要影响高频段频响函数。这与主轴系统固有特性分析结果一致，验证了固有特性分析的正确性和有限元法求解频响函数的有效性。

［1] 关锡友，孙 伟.数控机床主轴系统动力学特性分析方法研究［J] .机械强度，2009，31(4):629－633.

［2] 高尚晗，孟 光.机床主轴系统动力学特性研究进展［J] .振动与冲击，2007，26(6):103 －110.

［3] 高尚晗，龙新华，孟 光.主轴－滚动轴承系统三种分岔形式［J] .振动与冲击，2009，28(4):59 －65.

［4] Li H Q，Yung C.Shin.Analysis of bearing configuration effects on high speed spindles using an integrated dynamic thermo-mechanical spindle model［J] .International Journal of Machine Tools＆ Manufacture，2004，44(4):347－364.

［5] Cao Y Z，Altintas Y.Modeling of spindle-bearing and machine tool systems for virtual simulation of milling operations［J] .International Journal of Machine Tools＆ Manufacture，2007，47(9):1342－1350.

［6] 杨明亚，杨 涛，汤本金，等.应用有限元分析系统计算车床主轴的动态特性［J] .机械工程与自动化，2007，1(3):41－44.