汽车动力总成悬置耐久性模拟试验研究

上官文斌， 谢新星， 丁 维， 黄 兴， 徐 驰

(1.华南理工大学 机械与汽车工程学院，广州 510640;2.宁波拓普声学振动技术有限公司，浙江宁波 315800)

汽车零部件的疲劳耐久性试验是整车耐久性试验的一个重要组成部分。一般其耐久性试验分为试车场试验与实验室道路模拟试验。其中试验室道路模拟试验由于具备周期短、复现精度高、试验强化程度可调等优点［1]得到了广泛的应用。

使用RPC(Remote Program Control)技术可再现悬置在道路上所承受的实际载荷［2]，RPC技术的实现过程有五个步骤［1]:① 实际道路载荷谱采集与编辑;②试验系统的频响函数建立;③ 道路模拟试验的初始驱动信号计算;④ 路谱迭代;⑤ 道路模拟试验:耐久性或振动噪声试验。本文开展基于RPC技术的悬置道路模拟试验研究以期验证动力总成悬置系统疲劳耐久性能。

一轿车动力总成悬置系统的布局为四点支撑:发动机悬置、变速箱悬置、前悬置和后悬置，其中发动机悬置为液压悬置。本文以发动机悬置为试验对象，研究悬置耐久性的道路模拟试验。试验过程中考虑了液压悬置阻尼特性及刚度非线性特性，探讨了实验中频响函数建立和路谱迭代方法;基于RPC技术对发动机悬置道路载荷谱进行了重构，重构的道路载荷谱达到了预期的精度要求;探讨了建立悬置路谱模拟试验的总载荷序列的方法。对液阻悬置的试验结果表明，所采用方法可成功用于悬置耐久性试验。

1 载荷谱的采集

道路载荷谱的采集一般在汽车试验场进行。试验道路覆盖了车辆使用过程中可能遇到的各种工况路面。典型工况路面有搓板路、石块路、高速路和方坑等。使用eDAQ ECPU－PLUS型数据采集系统，在试验场采集了悬置25种不同工况路面的道路载荷谱(下文简称路谱)。

试验车上发动机悬置力传感器布置如图1所示。力传感器通过螺栓安装在支架1和支架2上，传感器采集的是支架2作用在橡胶主簧上的力。

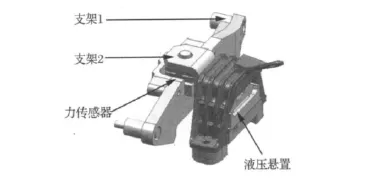
图1 试验车悬置上力传感器布置Fig.1 Force transducer layout on the engine mount

进行数据采集及后续的道路模拟试验时，要特别注意试验工装与夹具的设计。工装与夹具设计应满足以下原则:

(1)工装夹具的半功率带宽范围需与测试频率避开。根据工程经验，测试工装或夹具的固有频率应大于400 Hz以上，以确保测试系统所使用的工装在工作频率范围内不会产生共振;

(2)工装夹具的各向刚度足够大，确保受力后其变形对试验结果影响足够小;

(3)工装夹具加载约束面应尽量与实际零件安装接触面积大小接近;

(4)工装所传递的力应作用在悬置的弹性中心点上，以避免在力传递时产生附加的弯曲，以真实复悬置实际的应力水平。

2 路谱迭代

路谱迭代包括路谱编辑、频响函数模型建立、初始驱动信号获取以及迭代流程分析。

2.1 路谱编辑

对试车场采集到的原始路谱进行重采样、去均值、以及剪辑等编辑处理后得到台架试验的目标响应信号。原始路谱中有很多时间段的载荷非常小，由于其对疲劳损伤贡献很小以至于可以忽略不计，定义此类载荷序列为非损伤数据段。通过剪辑非损伤数据段可进一步实现缩短试验周期。图2为轻制动工况下的路谱剪辑图，图中灰色区域为被剪辑掉的路谱，剪辑前该谱试验时间为40 s，剪辑后试验时间为21 s，可知剪辑后该路谱试验时间减少了47.5%。剪辑过程中应注意保持原有载荷谱中各通道间相位关系。若过多的剪辑会导致有效谱丢失，各通道间相位错乱，使得原有路谱失真，这将不能完全反应实际路面的工况信息，对后续的疲劳试验精度产生较大影响。

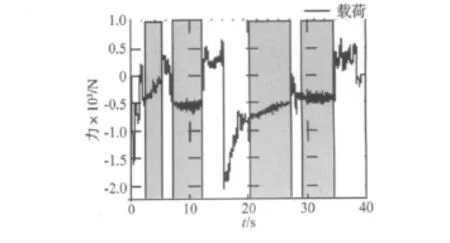
图2 轻制动工况路谱剪辑Fig.2 Road spectrum for moderate brake condition

通过对比编辑前后疲劳损伤差异可近似检验剪辑效果［3]。假设在基于相同材料S－N曲线条件下，计算出剪辑前后的路谱疲劳损伤分布直方图。图3～图4为编辑前后的路谱疲劳损伤直方图，其中X轴代表力幅值，Y轴代表力均值，Z轴代表疲劳损伤值。从两图的疲劳损伤对比可知目标响应信号保留了原始路谱98%以上的损伤值。

2.2 系统频响函数模型建立

2.2.1 白噪声设计

在系统频响函数模型建立过程中，激振信号在整个目标频段必须包含足够的能量，使得该频段内所有频率都被激励出来以获得理想的频响函数。由于白噪声在单位频带内所包含的能量相等，因此选择其作为理想的激振信号源。白噪声设计主要有上下截止频率、幅值等参数。

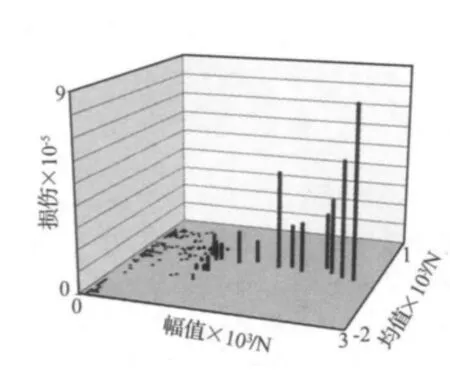
图3 轻制动工况路谱编辑前损伤直方图Fig.3 Damage histogram of the road spectrum under moderate brake condition before trimming

图4 轻制动工况路谱编辑后损伤直方图Fig.4 Damage histogram of the road spectrum under moderate brake condition after trimming

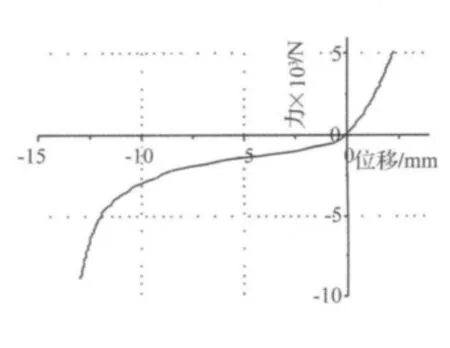
图5 发动机液压悬置Z方向静刚度曲线Fig.5 Static force －displacement curve of engine mount in direction Z

白噪声频带范围直接决定了测试频率范围。测试用的MTS三轴向弹性体测试系统所能达到的极限频率为80 Hz，而发动机悬置所受到的路面激励频率分布一般低于40 Hz［4]，故定义白噪声下截止频率为0，上截止频率为50 Hz即可满足频带范围要求。

白噪声峰值振幅大小与悬置静刚度特性紧密相关。下面以发动机悬置在Z方向白噪声峰值幅值确定为例，说明白噪声峰值振幅大小的确定方法。

悬置Z方向位移行程分为线性区、软拐点区、硬拐点区。图5为液压悬置Z方向静刚度曲线，图中正值区域表示悬置处于受拉状态，负值区域表示其处于受压状态，Z向线性静刚度为203.4 N/mm，线性区长度为10 mm。白噪声幅值在－2 034 N～0范围内时，悬置在Z向产生的位移可确保在悬置线性区行程以内，使悬置骨架不会撞击限位撞块。同时考虑悬置的Z向受力条件，从图5中可知悬置不受力时处于软拐点区域，即悬置在Z向零位时骨架已经和限位块接触。结合以上条件，白噪声幅值定义如图6所示，从图6中系统响应结果可知所定义的白噪声满足上述幅值条件。

系统传递函数的建立是基于系统在线性条件下进行的，若白噪声幅值取值过大或白噪声激励输入时悬置的行程已处于拐点区域，将使得系统出现明显的非线性特性，相应得到的频响函数质量较差。

2.2.2 频响函数建立方法

假设系统白噪声输入的激励通道数为m，则系统的输入激励为m×1阶信号矢量，记为x(t);假设系统的响应通道数为n，则系统输出响应为n×1阶信号矢量，记为y(t)。由于输入通道数小于或等于响应通道数，故有n≥m。分别对两组信号矢量x(t)、y(t)进行傅里叶变换(FFT)得到结果分别记为X(f)、Y(f)。任意两个经FFT变换的矢量X(f)和Y(f)的谱矩阵定义［5]为:

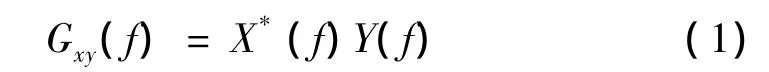
其中f为频率，*表示复数共轭运算，根据式(1)可求得系统输入信号自谱Gxx(f)、输出信号的自谱Gyy(f)、输入输出信号互谱Gxy(f)。

系统的频率响应函数矩阵H(f)定义为:

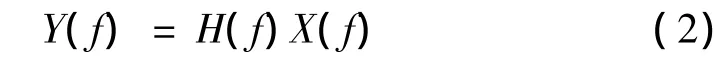
由式(2)可得输入输出信号之间的互谱和输入信号自谱的关系式:

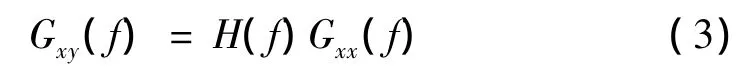
图7为系统Z通道白噪声输入信号自谱与输入输出信号之间互谱图。从图中可见输入白噪声信号与输出信号之间具有一定的滞后相位角，在目标频带内随着频率的增加，相位角也相应增加。系统滞后相位角大小主要受液阻悬置阻尼特性影响。

试验台系统频响函数被定义为:

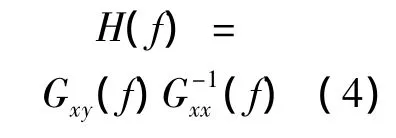
图8为系统Z通道频响函数模型，从图可见，频响函数曲线较为平滑，表明系统在感兴趣频带范围内不存在严重的非线性影响及无明显的外界干扰噪声。

2.2.3 频响函数检验

通常用多段平均相干函数来检验系统频响函数的有效性，相干函数定义［6]如下:

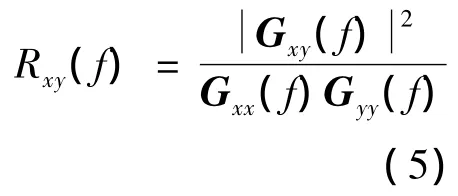
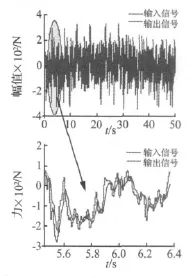
图6 Z通道输入的白噪声信号与系统响应信号的时域波形Fig.6 The time domain waveform of the white noise and the system response signal of channel Z

上式中Gxx(f)、Gyy(f)分别为输入信号自谱与输出信号自谱，Gxy(f)为输入输出信号互谱。相干函数在多段平均情况下才有意义，此时相干函数值0≤Rxy(f)≤1。相关系数远小于1时，表明系统输入信号中有别的噪声信号干扰或系统是非线性的。通常情况下要求相关系数大于0.8。本实验建立的系统Z通道相干系数见图9。由图可见，在0～50 Hz频率范围内系统相干系数保持在0.9以上，表明所测得的系统频响函数是可靠的。

2.3 初始驱动信号获取

计算初始驱动信号之前，首先须获得频响函数逆矩阵。早期的试验系统要求频响函数矩阵是方阵，即要求系统响应通道数量等于系统作动缸数量。这样频响函数逆矩阵可以直接通过矩阵求逆得到。随着技术的进步和发展，目前设计的台架实验平台可以实现目标响应通道数多于作动缸的数量。这种情况下频响函数矩阵将不再是方阵，此时可以通过伪矩阵求逆法来求解频响函数逆阵。系统的频域逆模型为:

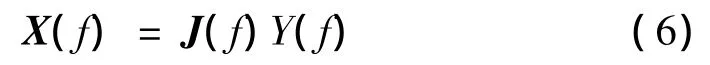
其中:Y(f)为目标响应信号的傅里叶变换;J(f)为系统频响函数逆矩阵，其由公式［5]计算得到:

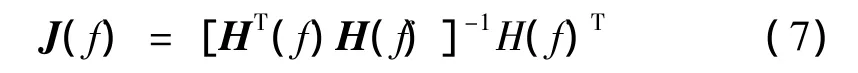
上式中H(f)为系统频响函数矩阵。

时域中理想初始驱动信号x0由下式计算:

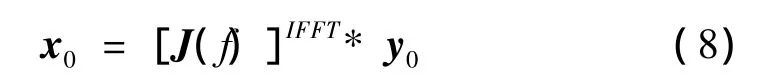
其中y0为目标响应信号，IFFT为傅里叶逆变换，*为时域卷积运算符号。

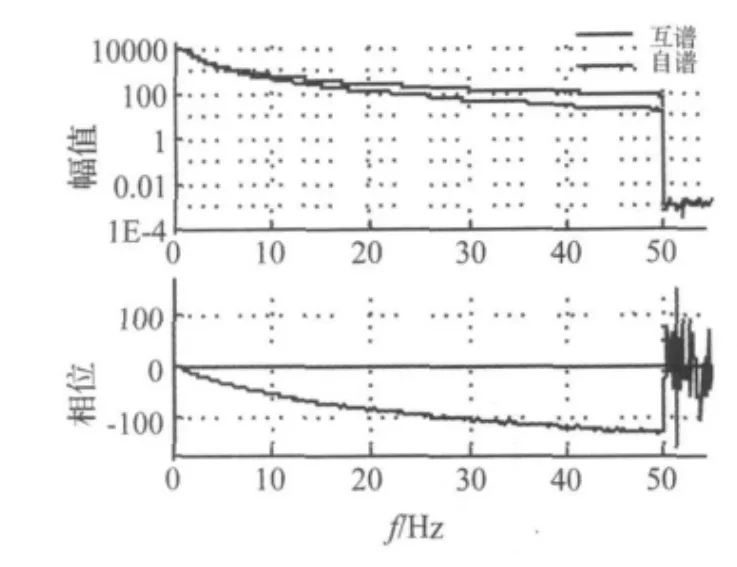
图7 Z通道输入信号自功率谱与输入输出信号互谱Fig.7 Autopower spectrum density of the input signal and cross spectrum density between the input and output signal of channel Z

图8 Z通道频响函数模型Fig.8 The frequency response function of channel Z

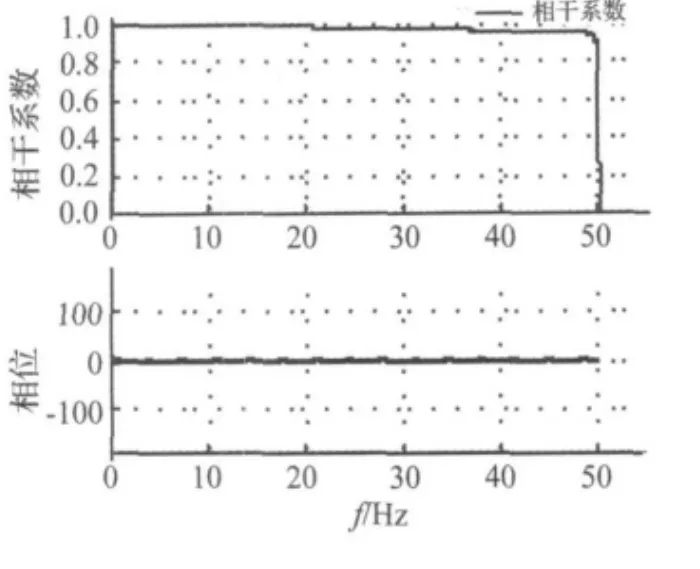
图9 Z通道相干函数Fig.9 The coherence function of channel Z

在本试验所采用的试验台架系统中，作动缸数量为3个，输出通道为3个。试验中每个作动缸输入信号为力时间驱动信号，响应信号为力－时间信号和位移－时间信号，其中力－时间反馈信号为主要的响应信号。频响函数矩阵H(f)为3×3阶矩阵，因此可通过上述矩阵求逆法来得到频响函数逆阵，进而求得初始驱动信号。为了防止过载，一般在理想初始驱动信号上附上一定的增益值后得到实际的初始驱动信号，其将作为迭代过程中首次迭代的输入信号。增益值取值范围为0～1。

2.4 迭代流程

道路模拟试验迭代运算的目的是为了获得各个工况路面的最终驱动信号。各个工况的驱动信号输入下，整个试验系统是非线性的，而前述频响函数矩阵的获得是基于系统为线性的，因此必须通过迭代的方法校正计算模型与实际系统模型之间的差异。

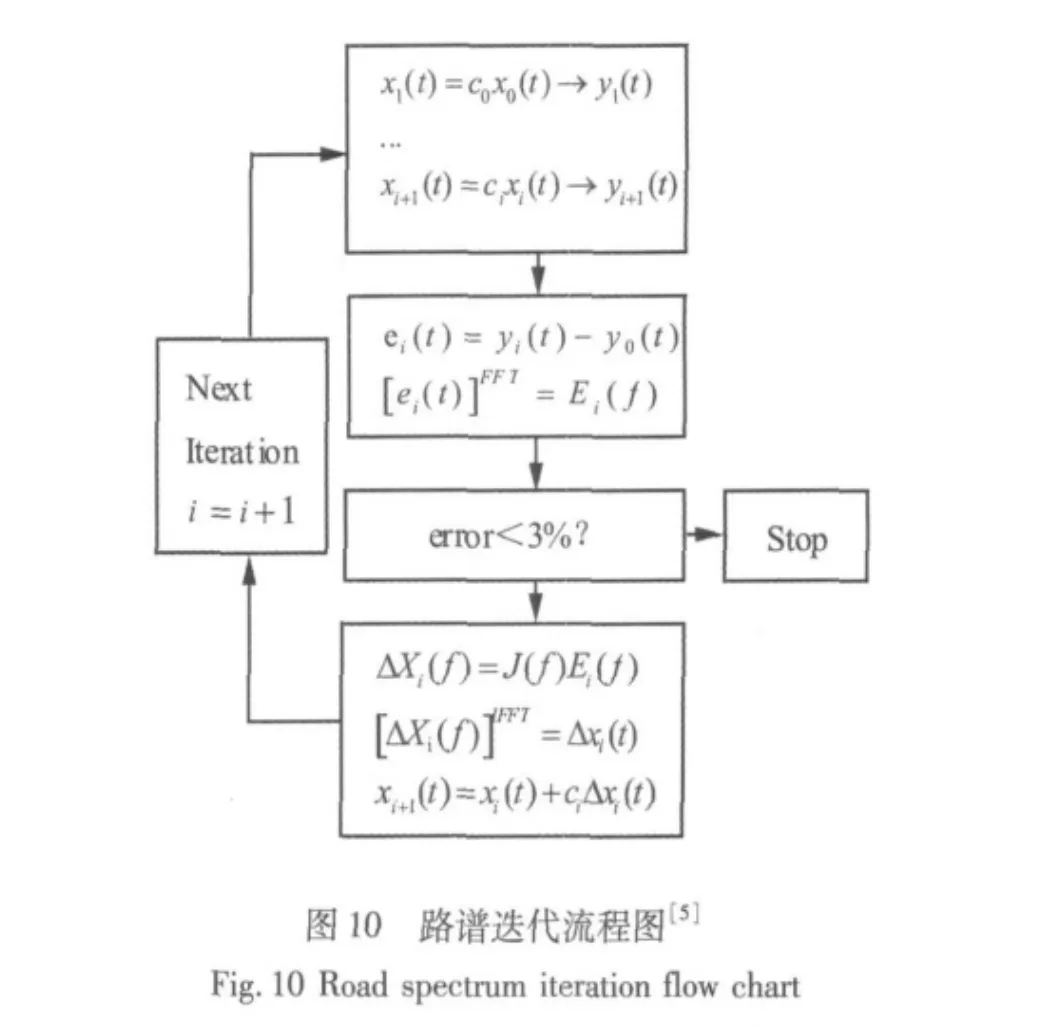
路谱迭代流程图如图10所示。每次迭代后系统会产生新的驱动信号xi(t)和响应信号yi(t)，将实际响应信号yi(t)与目标响应信号y0(t)之间的时域误差值ei(t)的傅里叶变换Ei(f)和频响函数逆矩阵J(f)进行频域乘积运算，计算得到系统频域的驱动信号增量ΔXi(f)，通过对其进行傅里叶反变换运算即可得到系统时域的驱动信号增量Δxi(t)。应用附带一定增益值ci的驱动信号增量来修正前一次的驱动信号进而得到新的驱动信号xi+1(t)。反复循环直至实际响应信号yi(t)与目标响应信号y0(t)之间的精度误差满足设定的要求时，一个迭代循环完成，系统输出最终驱动信号。

采用增益值来控制驱动信号增量的幅度是必要的。在修正驱动信号时若满载加载驱动信号增量，即增益值为1时，系统误差经常无法控制，此时可能会导致试件破坏或试验中断。鉴于上述原因，首次迭代增益值设置为较小值，随着迭代次数的增加，增益值可适度增大，如此可确保一定的迭代效果同时也可减少试验时间。

图11为石块路面工况Z向路谱迭代效果图，从图中可知，经过迭代后最终驱动信号对应的实际响应信号能够与目标响应信号很好地吻合起来。

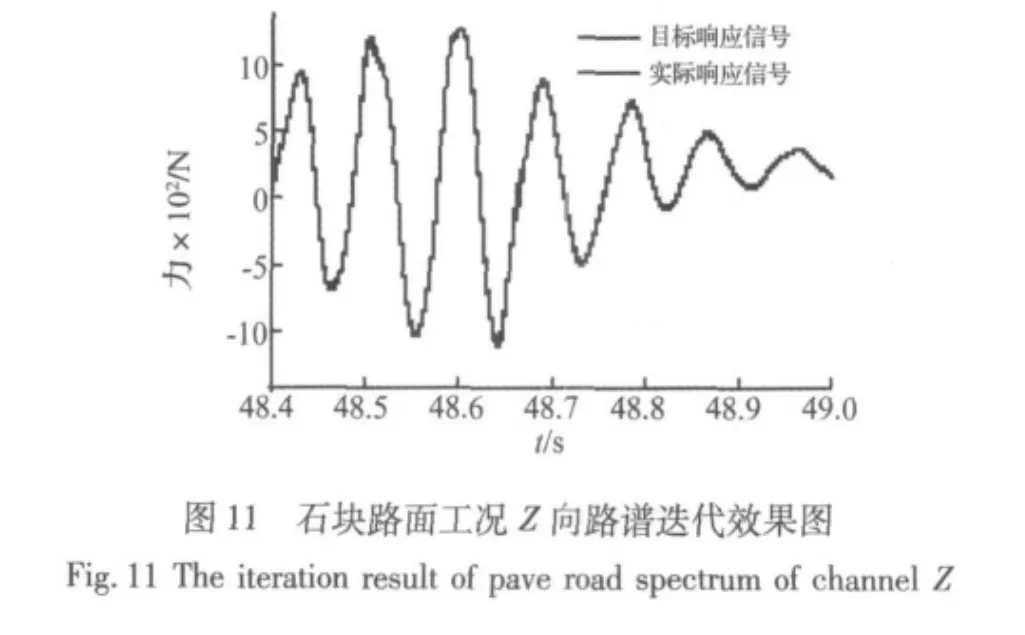
将实际响应信号yi(t)与目标响应信号y0(t)之间的时域误差均方根值作为迭代误差，并以其接近于零的程度来判断是否收敛。迭代误差定义［7]如下:

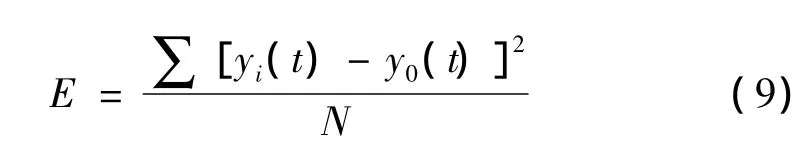
其中yi(t)为第i次迭代后得到的实际响应信号;y0(t)为目标响应信号;N为信号谱离散点数。

迭代误差反映了实际响应信号与目标响应信号在整个时间历程上偏差值的大小。如图12所示为石块路面工况路谱迭代过程误差控制图，图中可知试验迭代误差被控制在3%以内。各种工况迭代完成后均达到令人满意的误差精度要求。

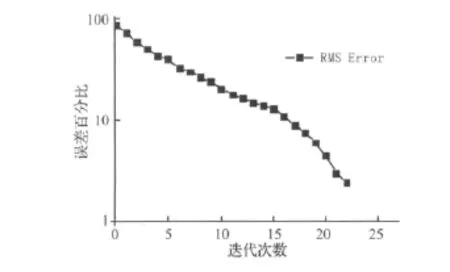
图12 石块路面工况Z向路谱迭代误差控制图Fig.12 The iteration RMSerror of pave road spectrum in of channel Z

2.5 总载荷序列编排

根据疲劳损伤积累理论，以大载荷工况与小载荷工况合理分布，避免极限工况集中出现为原则，将各路面工况驱动信号以重复一定次数的形式进行放大，并考虑车辆各种工况的实际使用频率，对迭代过程得到的各种工况路面的驱动信号进行编排得到总载荷序列。总载荷序列能近似等效模拟车辆实际路面行驶里程105km。

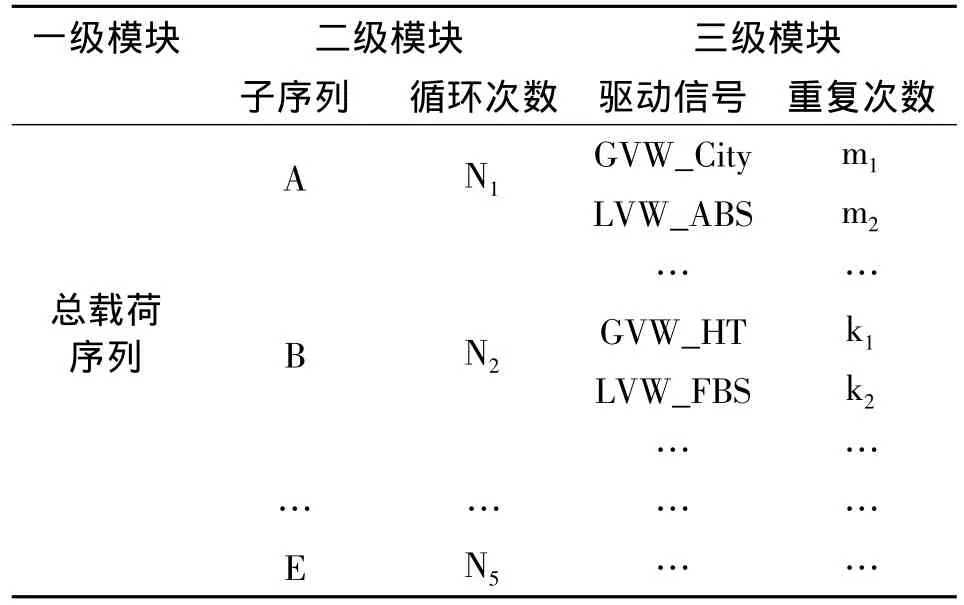
表1 载荷序列框架表Tab.1 Test sequence ＆ block frame

表1为总载荷序列框架表，由表可知总载荷序列结构由三级模块组成。其中一级模块为待试验的总载荷序列;二级模块为子序列模块，一共分有5个子序列，试验中每个子序列循环一定的次数N;三级模块下为25种路面工况的驱动信号，试验中每种工况驱动信号对应重复一定的次数，表中列出的典型工况驱动信号有重载城市道路工况驱动信号GVW_City、轻载ABS工况驱动信号LVW_ABS、重载高扭矩工况驱动信号GVW_HT等等。

3 悬置道路模拟试验结果分析

本文进行液阻悬置道路模拟试验系统为MTS833三轴向弹性体测试系统。它是一套以液压为动力，由电子控制并具有伺服功能的机械作动系统。该系统配置的RPC软件能够按照预定程序持续生成特定指令信号、实时监控反馈信号和对随机信号进行分析处理等基本功能，同时还具有迭代运算等特殊功能。

在进行疲劳试验时所采用的工装、安装方式、预紧扭力等条件需与迭代过程保持一致，为减小外界干扰对系统的影响，根据第2节中论述的方法，对一发动机液阻悬置进行了道路模拟试验。

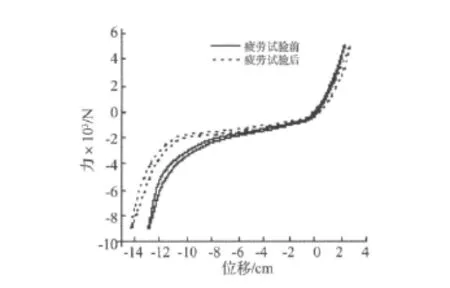
图13 试验前后悬置Z方向静刚度测试曲线Fig.13 Static force-displacement test curve for engine mount in direction Z before test and post-test

对所研究的液阻悬置，试验总载荷序列100%完成后，其未发现有液体渗漏、支架断裂和橡胶脱胶等迹象，同时悬置主簧蠕变量约为2.4 mm，蠕变量在预期控制范围之内。

但试验后悬置Z方向静刚度与初始静刚度相比降低30.4%，X和 Y方向分别降低了22.7%和15.3%。而悬置设计要求控制疲劳试验前后的各方向静刚度变化在25%以内，可知其Z方向静刚度下降略大。图 13为试验前后悬置Z方向(主方向)静刚度曲线变化图。由图可见，悬置在受压工况下线性段增长。其原因主要是下限位撞块出现裂纹引起的。如图14所示，在橡胶主簧附近撞块表面出现了约3 mm长度的橡胶裂纹。

图14 试验后悬置撞块表面裂纹Fig.14 The crack at the surface of the mount

后续的疲劳整改措施应以控制静刚度下降率为主要目标，改进限位撞块设计，并适当控制该类橡胶材料裂纹扩展速率，以进一步提高悬置的疲劳性能。

4 结论

(1)探讨了基于RPC技术的悬置道路模拟试验频响函数建立方法和路谱迭代理论，详细讨论了频响函数的建立、初始迭代信号的建立与总载荷序列的编排等;

(2)讨论了道路模拟试验中悬置工装夹具设计原则，本原则对其他车用橡胶减振元件的试验工装夹具的设计具有参考意义;

(3)液压悬置的阻尼特性和刚度非线性特性影响着系统PID调节与白噪声设计。试验中解决了因悬置本身特有属性而带来一系列问题，如传递函数有效建立及迭代收敛性等。

［1] 彭 为，靳晓雄，孙士炜.道路模拟试验中道路载荷谱的选择方法［J] .上海工程技术大学学报，2004，18(1):6－9.

［2] 梁荣亮，李孟良，过学迅，等.基于RPC技术的道路模拟试验载荷谱重构方法研究［J] .汽车科技，2008，6:42－44.

［3] Dodds C J，Awate C M.On the statistical properties of component response to road inputs［C] //. Proc. 6th International Conference on Durability ＆ Fatigue，Cambridge，2007.

［4] Dodds CJ，Ward CW.The development of test technology in vehicle Ddynamics［J] .SIAT，2005.

［5] Dodds CJ，Plummer A R.Laboratory road simulation for full vehicle testing:A review［C] //. In Symposium on International Automotive Technology，Pune，India，2001，47(1):487－494.

［6] Craig J，Dodds C J.The application of cross spectral analysis in the identification of vehicle characteristics［J] .FISITA Paris，1974.

［7] 杜永昌.车辆道路模拟试验迭代算法研究［J] .农业机械学报，2002，33(2):5－7.

［8] Styles D D ，Dodds C J.Simulation of random environments for structural dynamics testing［J] .Experimental Mechanics，1976，12:416－424.