基于遗传算法的磁流变阻尼器Bouc-Wen模型参数辨识

刘永强，杨绍普，廖英英，张耕宁

(石家庄铁道大学，石家庄 050043)

磁流变阻尼器是一种智能化的半主动控制实现元件，通过控制线圈中电流指令的大小可以改变磁流变液所处环境的磁场强度，磁场强度的大小直接影响着磁流变液的粘度系数，即影响着液体流经阀门的速度，从而实现阻尼器输出阻尼力的控制。磁流变阻尼器以反应速度快，消耗能量少和控制范围广等优点著称［1，2]，但由于其特殊的力学特性——滞回特性［3]，使得它的数学模型十分复杂。其中，Bouc-Wen模型就是较为典型的一个，该模型包含有8个未知参数，再考虑电流大小、活塞速度和激励等因素，参数识别起来比较困难。

国内外相关学者对此进行了大量的研究。Ikhouane等人［4，5]曾采用解析的方法对 Bouc-Wen 模型的参数识别过程做过详细的阐述，但由于解析法需要进行大量的假设和定义，过程较为复杂，因此通用性不佳。Spencer和 Dyke 等人［6，7]将 Bouc-Wen 模型中的参数均作为常值，利用有约束的非线性优化算法进行识别，虽然简单易行，但识别精度不高，且由于不含电流项所得到的模型无法应用于半主动控制。欧进萍、Shen、Liu 以及 Jansen 等人［8～11]曾将部分参数视为电流的函数，在此假设的基础上利用普通优化算法对参数进行识别，但值得指出的是普通优化方法在多变量识别方面局限性较大，识别精度较低，且通用性差。

本文拟通过对Bouc-Wen模型的结构和力学特性进行分析，采用擅长解决多变量优化问题和全局优化问题的遗传算法对模型的参数进行辨识，并确定了α，c0，k0三个参数与电流指令间的函数关系和其余5个参数的值。

1 磁流变阻尼器力学试验

磁流变阻尼器的结构如图1所示，利用MTS力学性能测试试验台测量其输出阻尼力，激励采用正弦信号x=A sin(2πft)。共进行了5组试验，分别为:A=5 mm、f=0.5 Hz，A=10 mm、f=0.5 Hz，A=20 mm、f=0.5 Hz，A=10 mm、f=1 Hz，A=10 mm、f=1.5 Hz。每组激励下分别取0 A～3 A范围内7个电流指令进行测试，共得到35组数据。其中，A=10 mm、f=0.5 Hz激励下的位移－阻尼力和速度－阻尼力曲线如图2和图3所示。由图中发现，当电流为3 A时，磁流变阻尼器输出的阻尼力达到了饱和。

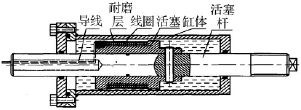
图1 磁流变阻尼器结构Fig.1 The structure form of the MR damper

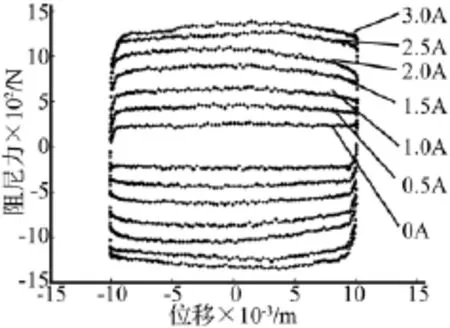
图2 位移－阻尼力试验曲线Fig.2 Displacement-damping force test curve

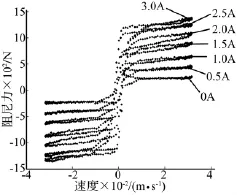
图3 速度－阻尼力试验曲线Fig.3 Velocity-damping force test curve

2 磁流变阻尼器Bouc-Wen模型及数值仿真

Bouc-Wen模型最早由 Wen于1976年提出［12]，它由滞回系统和弹簧、阻尼器并联而成，如图4所示。Bouc-Wen模型能够很好地模拟滞回特性，且通用性强，易于数值处理。其力学模型描述为:

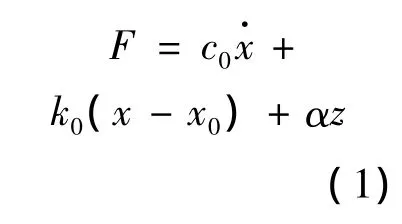
其中，滞回变量 z由下式决定

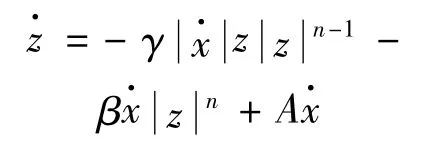
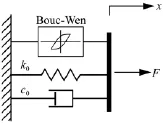
图4 Bouc-Wen模型结构Fig.4 Bouc-Wen model structure

由于存在微分项，采用传统方法对 Bouc-Wen模型进行数值仿真存在困难。本文在SIMULINK环境下对Bouc-Wen模型进行设计，并采用4阶Runge-Kutta法对其进行数值仿真分析，如图5所示。

Bouc-Wen模型的创始人之一 Wen［12]认为 Bouc-Wen模型中参数γ，β只影响滞回环的形状，而不影响阻尼力的大小，参数n只影响从弹性区过渡到塑性区曲线的平顺性。

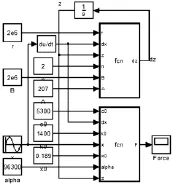
图5 Bouc-Wen模型在Simulink中的实现Fig.5 The realization of Bouc-Wen model in simulink

从试验曲线图1和图2中可以发现，电流I的大小对阻尼力幅值的影响较大。那么，到底Bouc-Wen模型中哪些参数与电流有关呢?Shen和 Jansen等［9，11]认为参数α，c0与电流之间存在着如下函数关系

而 Liu 等人［10]则将参数 α，c0，k0视为电流的多项式函数。因此，本文假设参数α，c0，k0与电流指令间存在着函数关系，但具体函数表达式待定。

3 Bouc-Wen模型参数辨识

Bouc-Wen 模型中待辨识的参数有 α，c0，k0，γ，β，A，n，x0共8个之多，辨识起来比较复杂。本文拟采用擅长多变量优化和全局搜索技术的遗传算法工具箱进行参数的识别工作。

1962 年 Holland［13，14]首次提出一种崭新的全局优化算法——遗传算法，它借用了生物遗传学的观点，通过自然选择、遗传、变异等作用机制，体现了自然界中“物竞天择、适者生存”进化过程，且计算速度快，效果比较理想，从而被迅速推广到优化、搜索、机器学习等方面，亦在复杂数学模型的参数识别方面得到广泛应用。MATLAB中遗传算法的命令为:

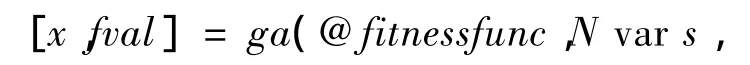
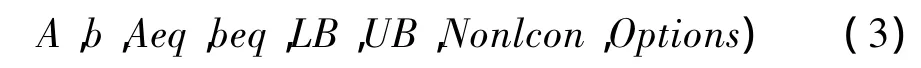
其中，fitnessfiunc为适应度函数;N var s为待求未知变量的个数;options为GA的结构参数。

GA的线性约束表达为:

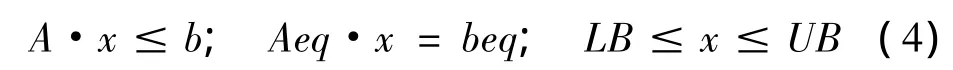
GA的非线性约束用Nonlcon函数来表达，它包括:

定义Bouc-Wen模型的适应度函数为:

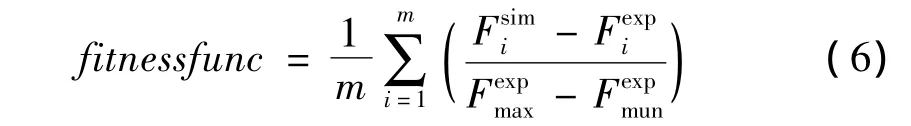
其中，m为试验数据点个数;Fsim和Fexp分别为通过仿真和试验得到的阻尼力大小;和分别为试验数据中最大和最小阻尼力值。

遗传算法是一种随机搜索、逐渐寻优的算法，其结果具有随机性。对任意一个MR阻尼器来说，由于Bouc-Wen模型不存在真实解，也就无法判断所识别的参数是否全局最优解，因此判断识别结果是否准确的唯一标准就是仿真结果与试验数据之间的吻合程度，即适应度函数值。另外，经过大量的仿真试验发现在保持其余参数固定不变的条件下，各参数的单调变化(单调递增或递减)都会引起滞回环形状或阻尼力幅值的单调变化。Bouc-Wen模型参数的这种特殊的单调特性使得只要目标函数足够小，得到的结果就应该在全局最优解的附近。

基于以上认识，本文拟采用逐渐缩小参数取值范围的方法来提高识别精度。利用幅值为A=10 mm，频率为f=0.5 Hz的正弦激励下电流为0 A～3 A的试验数据参与模型参数辨识，对辨识结果进行数值仿真，对比其他激励状况下的试验数据与仿真结果间的吻合情况，以验证辨识结果的正确性。

3.1 参数x0，n的确定

Bouc-Wen 模型共包括 c0，k0，x0，α，γ，β，A，n 等 8个未知参数需要识别。从图2和图3可以看到，磁流变阻尼器的滞回曲线不存在偏移现象，因此可知x0=0。对于固定的磁流变液，参数n为固定值，本文所用磁流变液为 n=2。因此，Bouc－Wen 还有 c0，k0，α，γ，β，A等6个参数待识别。

3.2 参数与电流间函数关系的确定

本文采用初始群体个数为N=50，采用实数编码方式，选择算法采用随机均匀分布选择;交叉采用分散交叉的方法，交叉概率取0.8(变异概率为0.2);变异采用高斯函数方法，生成服从高斯分布、均值为0的随机数加到父代上，尺度取0.5，压缩取0.7。

由文献［6，12] 可知Bouc-Wen模型中各参数均取正值，但由于无具体参数取值范围的界定，进行识别时应取较宽的取值范围，如:分别在电流指令为0 A～3 A条件下，对Bouc-Wen模型各参数进行GA辨识运算，迭代次数为500。

由于在参数取值范围较宽的条件下得到的参数适应度函数值较大，I=0 A时适应度值只能达到f1=5.41e－2。并且由于遗传算法在局部寻优能力较弱，因此需要缩小参数取值范围来提高识别精度。

从初步识别得到的参数值中选择各自的最小值作为低限值LB，最大值作为高限值UB，再次进行GA运算。不同的电流指令作用下，各参数的取值范围会稍有不同。以 I=0 A 时为例，c0，k0，α，γ，β，A 的线性约束取为:

此时得到的适应度值减小为 f2=1.38e－0.02。以此类推，逐渐缩小参数的取值范围，参数识别的精度也逐渐提高。经过10组运算后，适应度值减小到f10=1.36e－0.03。

运算得到的各参数值及误差如表1所示。绘制各参数随电流的变化曲线如图6所示。

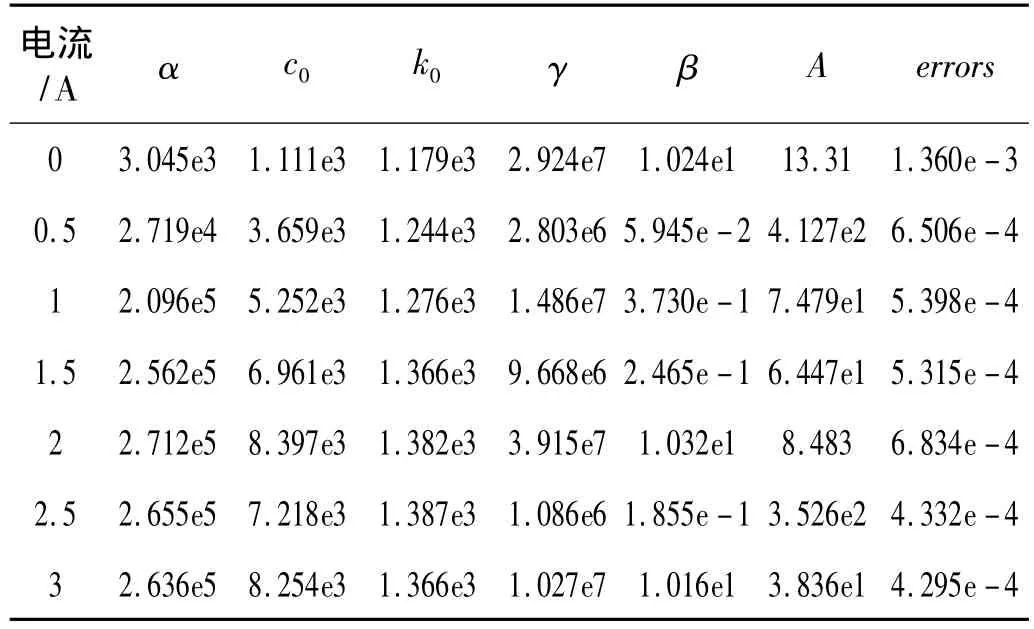
表1 GA运算得到的参数值及误差值Tab.1 The parameter and error values of GA

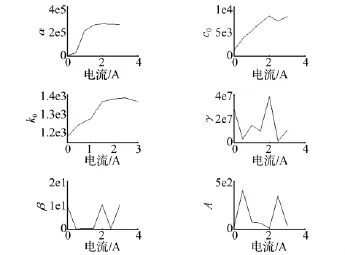
图6 各参数随电流的变化趋势Fig.6 The change trends of parameters under different

从图6可以发现γ，β，A为随机变化，无明显规律可循，α，c0，k0随电流的变化趋势则可以近似表达为3阶多项式形式:

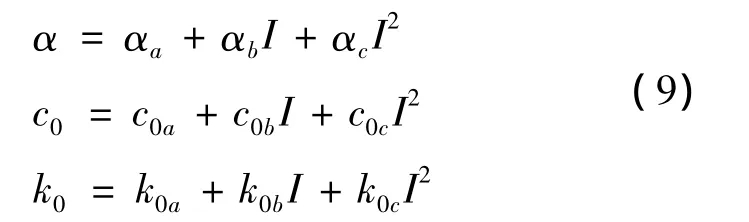
因此，需要辨识的参数由原来的6个增加为12个:

3.3 12个参数的确定

根据式(9)修改Bouc-Wen仿真模型，并根据式(6)中的适应度函数，定义包含所有电流的总适应度函数为:

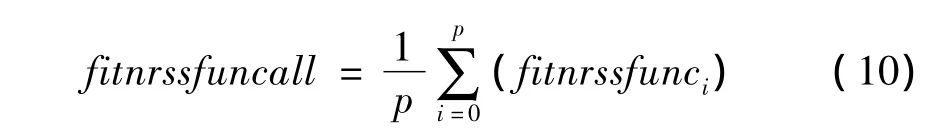
式中，p为试验中电流的个数，本文取p=7;fitnrssfunci为单个电流作用下的适应度值。

采用遗传算法对所有12个参数进行参数识别，采用逐步缩小参数取值范围的方法提高识别精度，式(9)中衍生出的9个参数可在［－1e8，1e8] 范围内取值，其余参数的取值范围为［0，1e8] ，最终得到总适应度值为fitnrssfuncall=1.107e－3时的参数识别结果为:

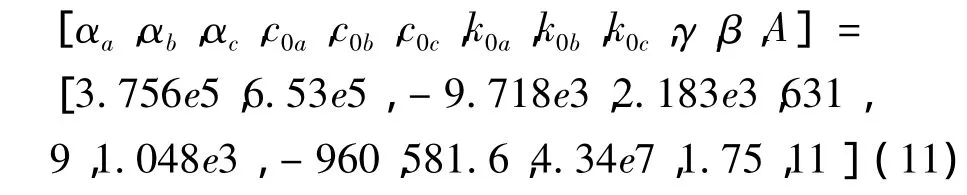
因此，Bouc－Wen模型最终可以表示为:

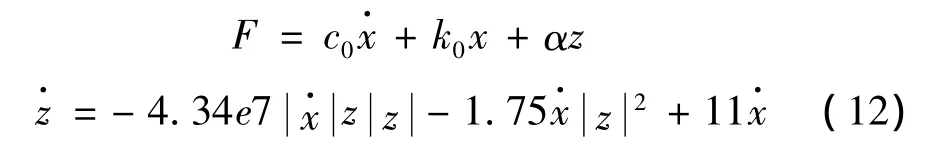
其中:

4 模型验证

模型验证分为拟合结果验证和预测验证两部分。拟合结果验证是为了验证对参数 α，c0，k0与电流间函数关系进行的3阶多项式假设的正确性;预测验证则是为了验证采用遗传算法辨识得到的Bouc-Wen模型能否真正表达该磁流变阻尼器的力学特性。

4.1 拟合结果验证

首先验证利用逐渐缩小参数取值范围的方法得到的Bouc-Wen模型的识别结果是否为全局最优解。

遗传算法的全局搜索能力较强，但局部搜索能力较弱，得到的结果无法保证为全局最优解。而模式搜索(Pattern Search，PS)则在求解全局最优解方面表现优异，但它对初始值的设定依赖性较强。因此本文利用遗传算法的结果作为模式搜索的初始值，较宽的取值范围内搜索全局最优解，以验证遗传算法结果的正确性。

按照式(7)设定为参数的取值范围，将式(11)作为初始值，采用模式搜索法得到的近似的全局最优解为:

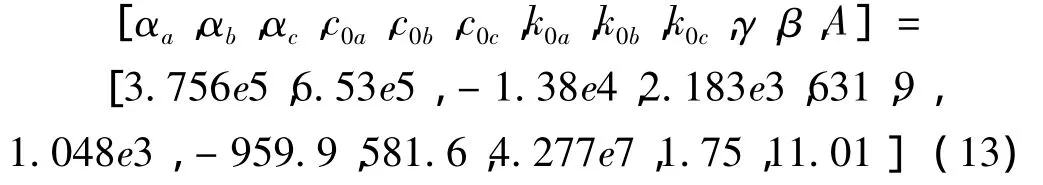
对比式(11)和式(13)中的结果，可以发现二者的结果基本相同，由此可以证明利用逐步缩小取值范围的方法提高Bouc-Wen模型参数识别精度的方法是可行的，由此得到的解在全局最优解的附近。

对式(12)所示的Bouc-Wen模型进行数值仿真分析，采用 Runge-Kutta法进行定步长求解，步长取为1 e－2 s，仿真时间为2 s，以获得与试验数据点个数相同的仿真值。当正弦激励幅值为A=10 mm，频率为f=0.5 Hz时，分别绘制仿真与试验数据的位移－阻尼力和速度－阻尼力曲线图，如图7所示。

图7 A=10 mm，f=0.5 Hz时仿真值与试验数据对比Fig.7 Comparation between simulation results and experiment data when A=10 mm，f=0.5 Hz

从图中可以看出，仿真结果与试验数据基本吻合，由此可见本文对函数关系的假设是合理的，所得到的曲线拟合和辨识结果均满足要求。

4.2 预测结果验证

由于Bouc-Wen模型的参数是通过振幅为A=10 mm，频率为f=0.5 Hz的正弦激励下的试验数据获得的，因此需要用其他幅值和频率下的试验数据进行验证才能证明该模型的正确性。

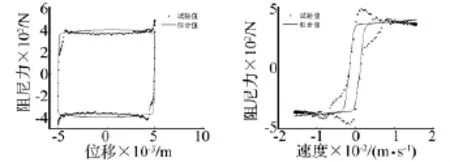
图 8 A=5 mm，f=0.5 Hz，I=0.5 A时仿真值与试验数据对比Fig.8 Comparation between simulation results and experiment data when A=5 mm，f=0.5 Hz，I=0.5 A

预测结果验证，即将数值仿真结果分别与 A=5 mm，f=0.5 Hz，A=20 mm，f=0.5 Hz，A=10 mm，f=1 Hz，A=10 mm，f=1.5 Hz正弦激励中不同电流指令作用下的试验数据进行对比，如图8～图11所示。

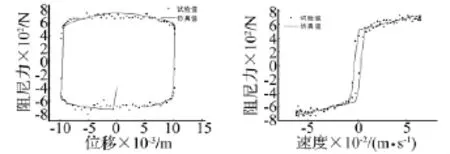
图 9 A=10 mm，f=1 Hz，I=1 A时仿真值与试验数据对比Fig.9 Comparation between simulation results and experiment data when A=10 mm，f=1 Hz，I=1 A

图 10 A=20 mm，f=0.5 Hz，I=1.5 A 时仿真值与试验数据对比Fig.10 Comparation between simulation results and experiment data when A=20 mm，f=0.5 Hz，I=1.5 A

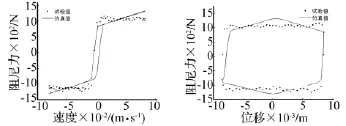
图 11 A=10 mm，f=1.5 Hz，I=2 A 时仿真值与试验数据对比Fig.11 Comparation between simulation results and experiment data when A=10 mm，f=1.5 Hz，I=2 A

从图8～图11中可以看出，本文通过遗传算法识别出的Bouc-Wen模型不仅与参与辨识的试验数据吻合较好，而且对其他幅值和频率的正弦激励下的MR阻尼器的动力学响应也能准确反映。

5 结论

本文在基于Bouc-Wen模型部分参数与电流指令间存在函数关系的假设上，通过遗传算法对模型的参数进行识别，采用逐步缩小参数取值范围的方法提高识别精度，并采用模式识别方法对该方法识别出的结果进行验证。最后，采用数值仿真的方法对函数关系的假设、曲线拟合及参数识别结果进行验证。结果显示，由于Bouc-Wen模型参数特殊的单调特性，通过逐步缩小参数取值范围来提高识别精度的方法可以找到近似的全局最优解。识别出的Bouc-Wen模型不仅与参与识别的试验数据相吻合，而且还可以准确表达其他幅值和频率正弦激励下的MR阻尼器动力学响应。

［1] 陈进新，王 宇.一种可应用于小阻尼力领域的新型磁流变液阻尼器［J] .振动与冲击，2009，28(2):155 －161，166.

［2] 施 亮，何 琳.磁流变阻尼器参数辨识方法研究［J] .振动与冲击，2009，28(1):131 －133.

［3] Yang S P，Li S H，et al.A hysteresis model for magnetorheological damper［J] ，Int J Nonlinear Sci Numer Simul，2005，6(2):139 －144.

［4] Ikhouane F，Rodellar J.Systems with hysteresis:analysis，identification and control using the Bouc-Wen model［M] .Chichester:John Wildy＆ Sons，Ltd，2007.

［5] Sireteanu T，Giuclea M，Mitu A M.An analytical approach for approximation of experimental hysteretic loops by Bouc-Wen model［J] .Proceedings of the Romanian Academy，Series A，2009，10(1):1 －12.

［6] Spencer B F，Dyke SJ，Sain M K，et al.Phenomenological model of a agnetorheological damper［J] .J.Engrg.Mech.，ASCE，1997(123):230－238.

［7] Dyke SJ.Acceleration feedback control strategies for active and semi-active control systems:modeling，algorithm development，and experimental verification［D] .University of Notre Dame，Indiana，1996.

［8] 欧进萍.结构振动控制——主动、半主动和智能控制［M] .北京:科学出版社，2003.

［9] Shen Y. Vehicle suspension vibration control with magnetorheological dampers［D] .University of Waterloo，Canada，2005.

［10] Liu Y Q，Matsuhisa H，Utsuno H，et al.Controllable vibration of the car-body using magnetorheological fluid damper［J] .Vehicle System Dynamics Supplement，2004(41):627－636.

［11] Jansen L M，Dyke SJ.Semiactive control strategies for MR dampers:comparative study［J] .Journal of Engineering Mechanics，2000(8):795 ～803.

［12] Wen Y K.Method of random vibration of hysteretic systems［J] .Journal of Engineering Mechanics Division，ASCE，1976，102(EM2):249 －263.

［13] Kristinsson K.System identification and control using genetic algorithms［J] .System，Man and Cybernetics，1992，22(5):1033－1046.

［14] Schneider T R.A genetic algorithm for the identification of conformationally invariant regions in protein molecules［J] .Acta Crystallographica Section D:Biological Crystallography，2002，58(2):195 －208.