夹心式复合变幅杆换能器频率方程的推导
秦 雷,王丽坤,唐会彦,孙百生
(北京信息科技大学 传感器重点实验室,北京 100101)
夹心式换能器是一类大功率发射换能器,这类换能器以较小的重量和体积获得大的声能密度,其发射灵敏度高,在水声、超声换能器领域应用较为广泛[1]。因此,其研究方法也多种多样,如:等效电路法[2]、有限元法[3-5]等。有限元法目前较常用,但在优化结构参数时由于需要大量改变某些参数,所以每改变一次参数都要进行全局运算,工作量较大[6]。等效电路法是分析夹心式换能器的解析法解法,理论较为成熟,计算简便并且容易被人接受,但由于引入过多的简化误差较大。为减少这种误差,研究者进行了许多理论研究。四川大学黄振伟[7]考虑了预应力螺栓对系统建模的影响,对33.66kHz的换能器进行了计算,其计算结果将误差由原来的2.69%降低到0.86%。北京大学栾桂冬[8,9]考虑了损耗对压电陶瓷的常用振动模的等效电路的影响,对于夹心式换能器的等效电路的推导有一定指导意义。传统等效电路法是将每一片压电陶瓷的六端等效网络推导出来,再根据电路中串并联关系得出多层压电陶瓷叠堆结构整体等效电路,然后同样根据电路串联理论,再叠加发射端、背衬以及预应力螺栓等影响,最后得出总体换能器等效电路。这样做有一定的缺陷。首先,没有考虑电极片的影响。在超声换能器以及频率较高的水声换能器中,陶瓷片的厚度不能远远大于电极片厚度时,电极片的影响是不能忽略的。其次,没有考虑多层陶瓷片经叠堆后,已经由一片薄圆片振动模态转化为长度伸缩振动模态,其振动方程已不能用原来薄圆片的振动方程来代替。本文首先根据传统等效电路方法推导了这种夹心式复合变幅杆换能器的等效电路,并得出频率方程。然后考虑电极片的影响,将多层压电陶瓷叠堆等效为一个由陶瓷和电极片构成的2-2型压电复合材料,应用压电复合材料的串并联理论以及等效参数理论,求出压电陶瓷叠堆的等效密度以及等效纵波声速等参数。将这些等效参数带入换能器频率方程,对其进行理论修正,提高了换能器频率方程的计算精度,可以更好的指导换能器制备。
1 夹心式复合变幅杆换能器结构
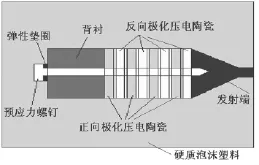
图1 换能器结构Fig.1 Structure of transducer
压电陶瓷叠堆以及由其构成的夹心式换能器的结构如图1所示,压电陶瓷晶片堆由多个压电陶瓷晶片机械上串联叠堆而成,有独立正负电极,相邻两片陶瓷之间极性相反构成电学并联结构。夹心式换能器包括:发射端、压电陶瓷晶片堆、背衬、预应力螺钉以及防水透声聚氨酯层,陶瓷晶片堆前后分别粘接发射端和背衬,发射端用轻金属制成,背衬由重金属制成,陶瓷片、发射端及背衬材料之间夹有薄铜片作为焊接电极引线用,其间均用环氧树脂粘接,以实现良好的振动传递。预应力螺钉用于固定发射端、晶片堆和背衬,同时施加一定的预应力于晶片堆,以增加晶片堆的抗张强度,提高发射功率。发射端采用倒喇叭变幅杆加小截面圆柱头复合结构,由于圆柱头的面积较晶片堆振动面减小,使辐射波束的开角增大,从而增大了换能器的指向性开角[1]。
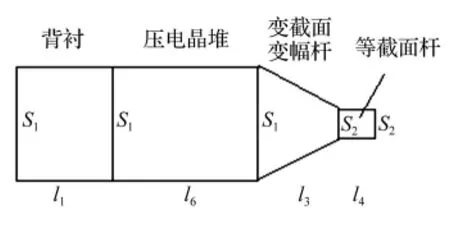
图2 换能器的简化模型Fig.2 Simplified model of transducer
2 夹心式复合变幅杆换能器的等效电路
实际的换能器由于结构复杂,在以下的讨论中,假定在所讨论的频率范围内,振子可以近似看作一维复合棒,即振子只沿轴向作一维振动。应用等效电路理论[5],把机械振动、电振荡以及机电转换过程用机电类比的原理,形象地组合在一个等效电路图中。根据以上近似条件,将换能器简化成图2所示四个部分,分别是:背衬、压电陶瓷晶片堆、圆锥形变幅杆以及圆柱形等截面杆,同时忽略其它边界条件的影响。
换能器发射时等效电路可画成图3的形式。
图3中Zs0,Zr分别表示背衬向外界辐射阻抗以及发射端向外界的辐射阻抗。
在以下讨论中,为计算简单,只考虑换能器在空气中的情况,即Zs0=Zr=0。图3所示的等效图又可进一步简化,令Zm1为背衬端施加于压电陶瓷叠堆的等效机械阻抗,Zm2为发射端施加于压电陶瓷叠堆的等效机械阻抗。其值分别为:
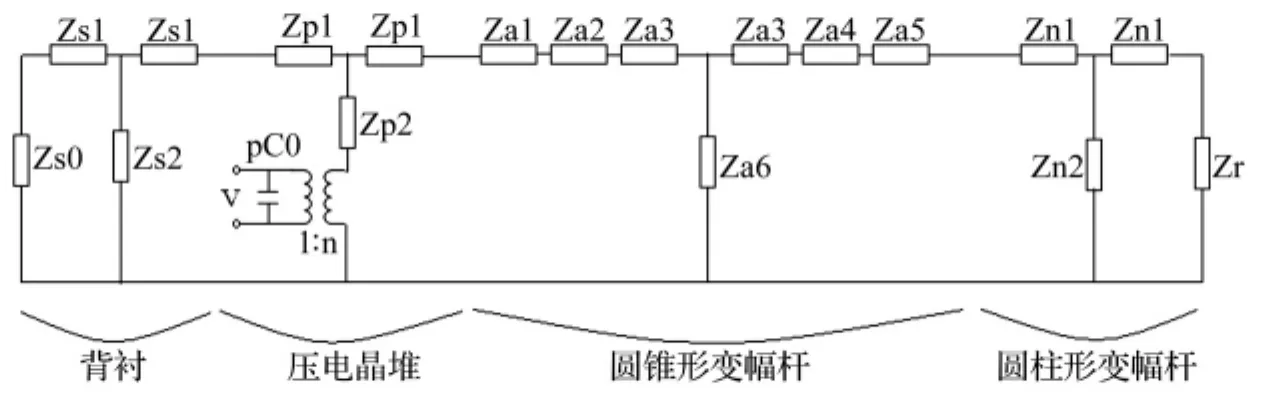
图3 换能器的等效电路图Fig.3 Equivalent circuit diagram of transducer
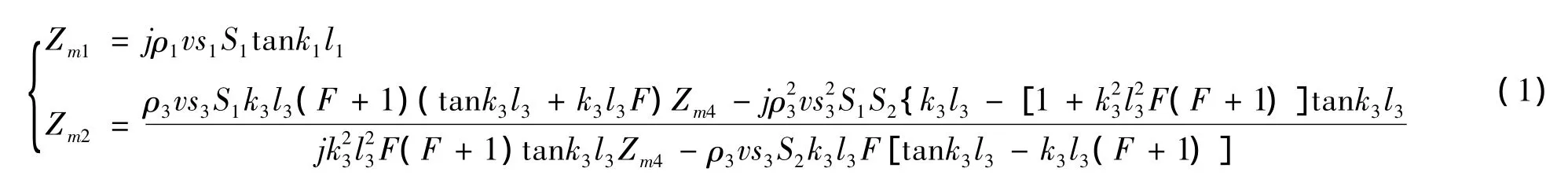
其中 F=r1/(r2-r1)为变幅杆延展系数,Zm4=jρ3vs3S2tan k3l4为发射端圆柱型等截面杆施加于圆锥型变幅杆的等效机械阻抗,脚标1表示背衬材料参数,脚标3表示发射端材料参数,ρ为材料密度,l为长度,S为面积为纵波声速,k=w/vs为波数。
3 夹心式复合变幅杆换能器的频率方程
在共振频率下,对于一个半波长振子,振动时两端振幅最大,中间存在一个振速为零的截面,称为节面。根据共振频率下动态回路中总机械抗为零,设Zm=Rm+jXm,又因为推导过程中未涉及损耗即机械阻为零,所以Zm=jXm,对节面左右两部分分别列方程得:
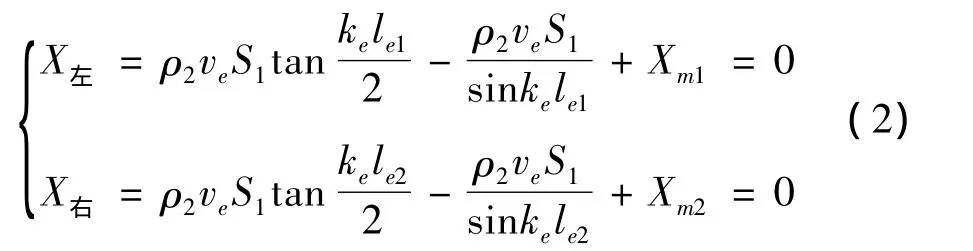
式中:le1,le2分别为振子截面两边陶瓷晶片堆的长度,le=le1+le1为陶瓷晶片堆的长度。化简(2)式得到换能器的频率方程:
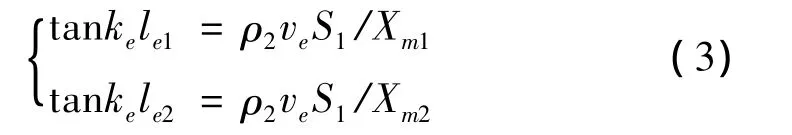
4 夹心式复合变幅杆换能器频率方程的理论修正
由于压电陶瓷晶片堆之间引入了黄铜垫片作为电极,而当电极片的厚度与单个陶瓷片的厚度可以相比时,电极片对压电陶瓷晶片堆性能的影响则不可忽略。因此对于公式(3)给出的换能器振子频率方程需要进行修正。公式中包含三个相关的参数ρ2、vse和ke,分别表示振子中压电晶堆的密度、纵波声速以及波数。引入黄铜垫片会导致这三个参数发生变化。公式中密度ρ2应修正为等效密度:
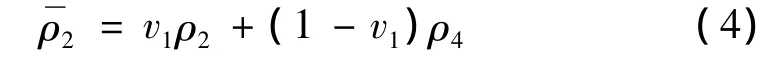
其中v1为压电陶瓷晶片堆中陶瓷体积百分比,ρ4为黄铜垫片密度。如图4所示,等效密度随着压电陶瓷体积百分比增加而线性减小。
陶瓷薄片经过叠加后构成长条形晶片堆,其振动模为电场平行于长度的长度伸缩模,对于晶片堆构成的压电体的纵波声速=,因此只要再求出压电体的等效弹性柔顺系数,就可求出压电晶堆的等效纵波声速。根据压电复合材料的串联理论[11],压电陶瓷片与黄铜垫片构成的压电振子可以等效成一种新的压电材料,从而求出这种新的压电材料的等效弹性柔顺系数
考虑到压电陶瓷片z向极化,只有z方向有电场,并且假设压电陶瓷片与黄铜垫片不存在切向应变。因此得到简化的压电陶瓷本构方程:
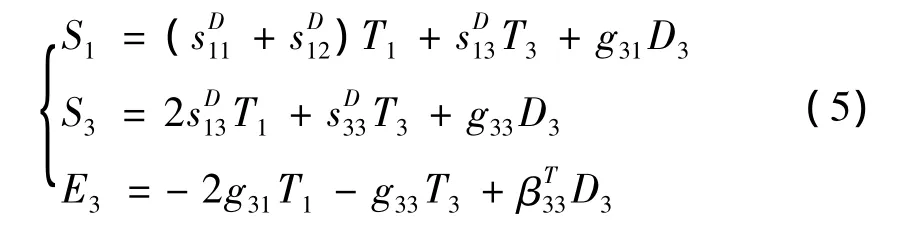
简化的黄铜垫片本构方程:
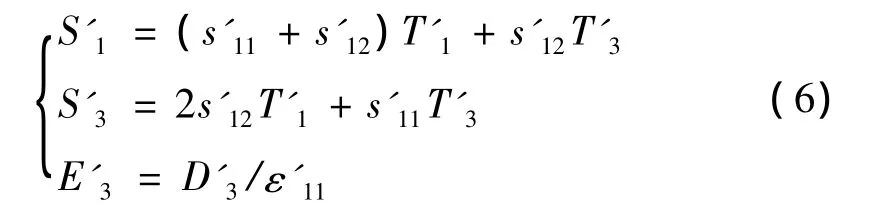
压电振子作为一个压电体,具有与压电陶瓷类似的本构方程:
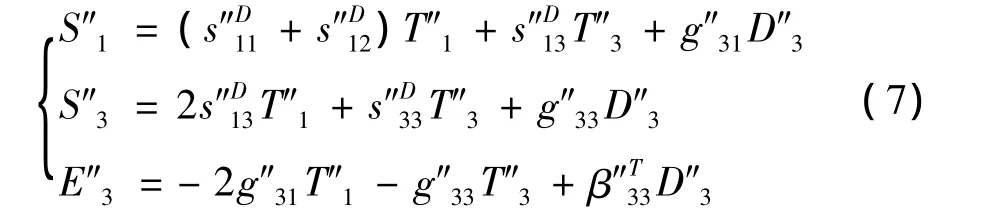
压电振子由压电陶瓷片和黄铜垫片在厚度方向串联,在其它两方向并联,因此可以作以下假设:
(1)电场加在压电陶瓷片和黄铜垫片串联结构上,且黄铜垫片内部电场为零,即作用于压电振子的电场等于压电陶瓷片电场,并沿z轴方向。同时,考虑将振子等效为压电体,那么在振子上与在相同体积的纯陶瓷上施加的电压一样的情况下,等效的振子内部电场为E″3=U/d,压电陶瓷片内部电场为 E3=U/(d·v1),其中U为施加在陶瓷上的电压,d为陶瓷片厚度。压电振子等效电位移等于两相材料电位移之和,且黄铜垫片内部电位移为零。所以:
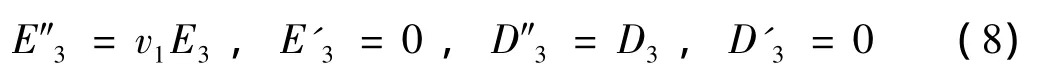
(2)压电振子的垂向应变为各相垂向应变之和,应力与两相材料的应力相等,即:

(3)压电振子的横向应变与两相材料各自的横向应变相等,两相材料的应力之和为总应力,即:
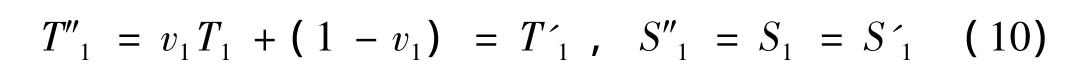
其中上标“″”代表压电振子等效参数,上标“'”代表黄铜垫片材料参数,无上标参数代表压电陶瓷参数。
综合(1)、(2)和(3)三条假设可得:
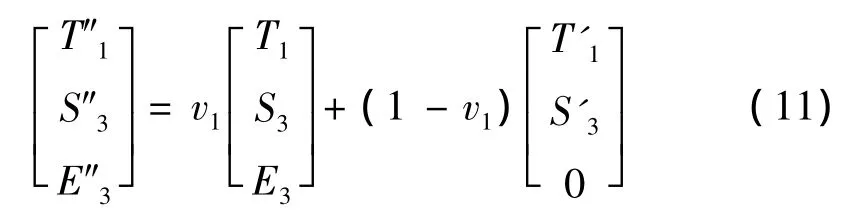
将式(5)、式(6)和式(7)以 T3,S1,D3为独立变量表出后,带入式(11)可得:

其中 s'11,s'12为黄铜材料的弹性柔顺系数为压电陶瓷材料的弹性柔顺系数。由公式(12)可以看出,陶瓷晶片堆作为一个整体其等效弹性柔顺系数只与两相材料的固有弹性柔顺系数以及两相材料体积百分比有关。图4给出等效弹性柔顺系数与压电陶瓷圆片体积百分比的关系,从图中可以看出随着压电陶瓷圆片体积百分比的增加,等效弹性柔顺系数呈线性减小。
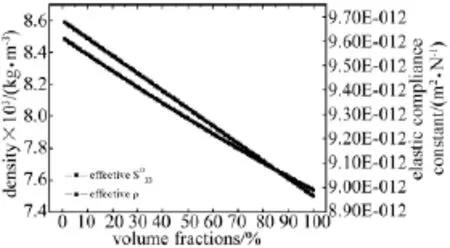
图4 压电晶堆等效密度与弹性柔顺系数与体积百分比关系Fig.4 The equivalent density and the elastic compliance constant with volume fractions
将以上三个修正的参数代入式(3)的频率方程后就可得到修正的频率方程:
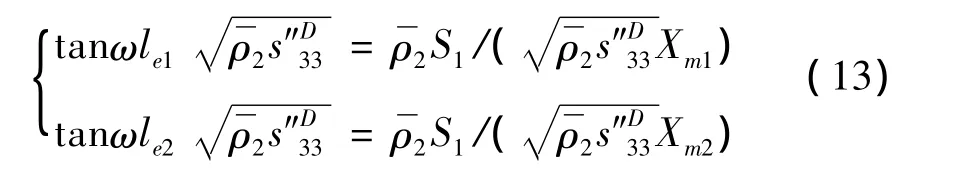
5 换能器频率方程的实验验证
夹心式复合变幅杆换能器中压电陶瓷选用PZT-4,它具有低的机械损耗和介电损耗、大的交流退极化场,并具有较大的介电常数、机电耦合系数和压电常数,适合于强电场、大机械振幅的激励,常用作发射换能器的换能材料。环氧树脂要有良好的粘接性、抗张强度,大功率发射时具有良好的性能,因此选用北京航空材料研究院的SY-37型透明环氧胶作为胶粘剂。发射端和背衬材料分别选用铝和钢,这样根据动量守恒定律,发射端与背衬的位移比约为3∶1。铜垫片选用0.2mm厚的黄铜片,以上五种材料的性能列于表1。

表1 换能器中用到的原材料性能Tab.1 Parameters of example used in transducer
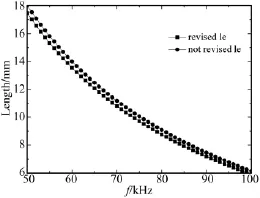
图5 修正前后le随频率变化曲线对比Fig.5 The frequency depends on length of stack
将表1中提供的材料参数代入式 (1)、式(12)和式(13),并设定背衬和发射端的尺寸分别为 l1=5.3 mm, l3=6 mm,l4=5 mm,r1=10 mm,r2=4 mm,考虑修正前后两种情况,可计算得到如图5所示的le随谐振频率变化规律曲线。由图中数据可看出,修正前后le随谐振频率变化规律基本相同,但得到的压电陶瓷晶片堆尺寸相差较大,这是由于在压电陶瓷和铜片构成的串联结构中,纵波声速相比纯陶瓷有明显降低。分别将两条曲线拟合为如下方程:
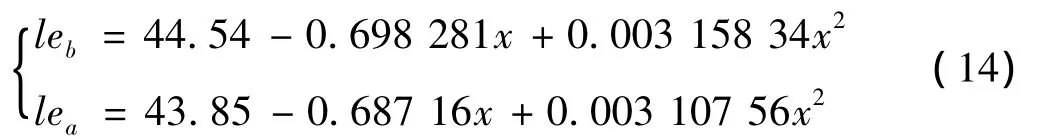
其中,leb表示未修正前计算出的压电晶堆尺寸,lea表示修正后计算出的压电晶堆尺寸,单位均为mm。x为晶堆预期的谐振频率,单位为kHz。
为验证以上频率方程,本文选取75 kHz为换能器的目标设计频率,选择8片1 mm厚的压电陶瓷片与8片0.2mm厚的黄铜片组成压电陶瓷叠堆,其总厚度为9.6 mm,实验制备出两个样品,用阻抗分析仪测试其空气中谐振频率均为75.6 kHz。将75.6 kHz分别带入(14)式的两个方程,可以得出修正前后压电晶堆的理论长度,修正前计算得到的厚度应为9.8mm,与压电陶瓷叠堆厚度相比误差为2.09%,修正后计算得到的厚度为9.66 mm,与压电陶瓷叠堆厚度相比误差仅为0.64%,可见上述理论推导以及修正较为合理,可以用来指导换能器的制备。
6 结论
本文对发射端叠加变幅杆式复合棒发射换能器进行了理论研究。推导了等效电路,并得出频率方程。同时考虑到黄铜电极片对振子密度以及等效声速等参数的影响,提出频率方程的理论修正。分析了换能器中压电振子尺寸随谐振频率变化的关系。研究表明,应用经过理论修正的频率方程可以得到误差为0.64%的计算结果,比未修改的误差有大幅下降,可以更好的用来指导实际换能器的实际制备。
[1] 何 涛,林书玉,梁召峰.多频扭转夹心式换能器研究[J] .陕西师范大学学报(自然科学版),2004,32(1):47-50.
[2] 顾晓丹,刘传绍,张昌娟.夹心式压电超声换能器的等效电路设计法[J] .声学与电子工程,2007,87(3):28-30.
[3] Zhang J D,Humphrey V F.3rd european comference on underwater acoustics[C] .Heraklion,1996,1013 -1018.
[4] Ring M D.Proceeding of the third international workshop on transducers for sonics and ultrasonics.M.D.Mc Collum[C] ,B.F.Hamonic and O.B.Wilson,ORLANDO,FLORIDA,1992,198-208.
[5] Quido Pucci.Undersea defence trchnology[M] ,1995,536-541.
[6] 莫喜平,姜广军.弯张换能器的等效电路支路阻抗分析方法[J] .应用声学,2001,20(2):12-17.
[7] 黄振伟,傅 波,穆 飞.夹心式压电超声换能器串并联传输矩阵设计法[J] .应用声学,2008,27(5):395-400.
[8] 栾桂冬,张金铎.考虑损耗的压电陶瓷常用振动模的等效电路(I)[J] .应用声学,1984,5(1):12-17.
[9] 栾桂冬,张金铎.考虑损耗的压电陶瓷常用振动模的等效电路(II)[J] .应用声学,1984,5(2):31-32.
[10] Mason W P.(ed),Physical acoustics,Vol.1 -Part A[M] .Academic Press,New York and London,1964.
[11] 秦 雷,李 莉,王丽坤.3-2型压电复合材料的静水压特性研究[J] .功能材料,2007,38(11):1824-1830.

