多体系统动力学研究进展
戎 保,芮筱亭,王国平,杨富锋
(1.南京理工大学 发射动力学研究所,南京 210094;2.南昌陆军学院,南昌 330103)
多体系统是以一定方式相联接的多个物体(刚体、弹性体/柔体、质点等)组成的系统。在兵器、机器人、航空、航天、机械等国防和国民经济建设中,诸如发射系统、飞行器、机器人、车辆、民用机械等大量机械系统均可归结为多体系统。随着国民经济和国防建设对机械系统产品动态性能要求的提高,需要对大型复杂机械系统动力学特性进行准确而快速地分析和预测。在这样的工程背景下,出现了多体系统动力学这一新的学科分支。
近年来,国内外诸多学者对多体系统建模、设计、控制、求解策略及其实验等方面进行了深入地研究,基于这一课题发表的文献层出不穷[1-5]。自1977年国际理论与应用力学联合会在德国慕尼黑发起第一次多体动力学国际研讨会[6]以来,关于多体系统动力学及其应用方面的国际会议也如雨后春笋般不断涌现[7-9]。现今多体系统动力学已成为现代力学的重要发展方向,各种新兴的研究方法层出不穷,出现了两个著名的专业学术国际期刊:Springer出版社的《Multibody System Dynamics》和英国机械工程协会的《Journal of Multi-body Dynamics》。
本文对近年来国内外多体系统动力学建模方法、求解策略、控制设计、软件开发及实验研究等方面的研究现状进行了较为全面地概括和总结,并简要展望了多体系统动力学的发展趋势。
1 多体系统动力学建模
多体系统动力学的核心问题是建模和求解问题,其系统研究始于20世纪60年代,早期研究对象是多刚体系统。Wittenburg[10]将图论方法引入多体系统动力学,出版了第一本多体系统动力学专著,奠定了多刚体系统动力学 Lagrange方法的基础。Kane[11]在对各种动力学原理进行分析比较的基础上,提出了兼有矢量力学和分析力学特点的Kane方法,并讨论了该方法在航天器动力学上的应用。Schiehlen[12]出版了第一本统一的多体系统动力学手册,有限元系统和连续系统可视为统一的等价模型。Nikravesh[13]出版了多体系统计算机辅助分析的第一本专著。Roberson等[14]讨论了多体系统的起源、刚体建模、线性化方程以及计算机模拟技术等。Haug[15]提出了多刚体系统建模的笛卡尔方法。贾书惠、刘延柱、洪嘉振等[16,17]各自出版了经典多体系统动力学著作,详细讨论了多刚体系统动力学的建模和计算问题。Huston和刘又午[18,19]在 Kane方法基础上,采用低序体阵列描述系统的拓扑结构,用Euler参数描述体间的相对方位,通过矢量求导与矩阵乘法运算的变换,形成了富有特色的面向计算机的Kane-Huston 方法。此后,袁士杰、陈乐生等[20,21]分别论述了多刚体系统动力学的相关研究成果。Shabana[22]详细阐述了多刚体系统计算动力学及其数值求解。De Jalón和 Bayo[23]提出了多刚体系统建模的自然坐标方法(又称完全笛卡尔坐标方法),并给出了一种满足实时仿真需要的高效求解策略。Stejskal等[24]从空间机构的CAD设计入手,给出了高、低副运动学约束的描述,并讨论了动力学分析及数值计算方面的问题。姚文莉、陈滨等[25]通过采用分段分析的方法得到了含摩擦的平面多刚体系统冲击问题的理论解。陈立平等[26]基于ADAMS软件阐述了多刚体系统动力学理论的工程应用。针对通常多体系统动力学方法计算速度随系统自由度增大而迅速降低从而难以满足复杂工程设计快速计算要求的情况,芮筱亭等[27,28]结合传递矩阵法计算效率高和逐步时间积分法应用范围广的优点,提出并逐步完善了多体系统离散时间传递矩阵法,实现了对一般多刚体系统动力学的高效快速计算。Wittenburg[29]全面系统地介绍了多体系统建模的图论方法,并讨论了多刚体系统接触碰撞动力学问题。Featherstone[30]论述了开环、闭环多刚体系统的正、逆向动力学及接触碰撞问题的算法。
随着国民经济和国防技术的发展,对很多工程问题,多刚体系统模型与实际相差甚远,满足不了工程精度要求,必须同时考虑部件大范围运动和构件本身变形的相互耦合作用,对柔性多体系统动力学或多刚柔体系统动力学的研究已越发凸显出其重要意义[31]。柔性多体系统是以各种铰接方式相联接的经历大运动的可变形物体和刚体所组成的系统,其是多刚体系统物理模型的精细化及自然的延伸和发展。
目前,柔性多体系统动力学通常采用Reyleigh-Ritz法、有限段法、有限元法、模态分析法等描述柔体变形,进而基于浮动标架法、旋转坐标法、绝对节点坐标法等方法建立柔性多体系统运动学和动力学方程[1]。浮动标架方法是在柔性构件上直接建立一个动参照系,将柔体的运动分解为随动系的牵连运动(大范围的刚性平动和转动)和相对于动系的相对运动(弹性变形)的叠加。浮动标架法适合于小变形物体所组成的系统。此类系统中柔体变形可通常按模态展开等线性方法处理,可很方便地把模态分析和实验模态识别等技巧推广到柔性多体系统动力学[1]。旋转坐标方法针对柔性构件上每个有限单元定义相应的动参考系。绝对坐标法将柔体的大运动及变形都用相对惯性坐标系的单元结点坐标表达,进而推出柔体的应变-位移关系,并在此基础上发展了能处理柔性构件大变形的非线性有限元模型。旋转标架方法及绝对坐标法与浮动标架方法相比较,具有惯性张量的平动部分是线性或常量,运动非线性效应如大变形、离心刚度等自动具有,并且精度随网格的细化而提高等优点[1,32]。但模态综合技术不易在旋转标架方法及绝对坐标法中使用[1]。总体而言,柔性多体系统动力学方程的建立远比多刚体系统动力学复杂,其计算规模和计算工作量也比多刚体系统动力学大得多,其理论也远不如多刚体系统那样完善。从本质上讲,柔体大范围运动与其变形运动之间的相互耦合,给柔性多体系统动力学建模与分析计算带来了许多困难[1-4,31]。
Shabana[32]、Huston[33]、Bremer[34]、黄文虎[35]、陆佑方[36]、洪嘉振[37]以及覃正等[38]在各自专著中详细讨论了柔性多体系统动力学建模理论和数值算法,上述论著已成为本领域的经典教材。Geradin[39]阐述了有限元方法在柔性多体系统动力学问题中的应用。Eberhard[40]结合了有限元和多刚体方法的优点,建立了多刚体/有限元混合算法,实现了高计算效率和高精度地解决柔性多体系统接触问题。Ambrósio[41-43]分别应用柔性多体系统动力学方法对车辆动力学和含复合材料的多体系统进行了深入研究。潘振宽等[44]研究了多体系统动力学动态最优化设计与灵敏度分析。Wasfy[45]、Sandu[46]分别研究了参数不确定性柔性多体系统动力学问题。Wittbrodt[47]描述了刚体有限元方法,并基于相似变换和铰坐标自动生成刚柔耦合系统动力学方程解决柔性多体系统动力学问题。Eberhard等[48]结合Krylov子空间方法和Gramian矩阵降阶方法提出了柔性多体系统模型缩聚的两步法,大幅度提高了大尺度系统的计算效率。齐朝晖等[49,50]提出了含非理想约束柔性多体系统递推建模方法,并对多体系统冗余约束和铰内摩擦接触给予了相应研究。Shabana等[32]将绝对坐标法应用于大变形的柔性多体系统动力学研究,在此基础上 YOO、李彬、刘锦阳、田强、陈立平、Laith[51-55]等将其推广到包含梁、板、壳等大变形柔性构件的多体系统。刘锦阳[56]研究了离心力和温度变化引起的附加弯曲变形对复合材料柔性多体系统振动特性的影响。王中双等[57]研究了键合图方法在机械系统动力学建模中的应用,提高了多体系统动力学分析的效率和可靠性。吴洪涛等[58]基于空间算子代数理论对多体系统正、反向动力学进行了设计与实现。蒋建平、刘又午、王树新等[59-61]分别应柔性多体系统动力学相关理论研究了航天器动力学问题。彭慧莲、王士敏、王琪等[62]用笛卡尔坐标阵描述系统的位形,根据局部方法的递推关系建立系统的约束方程,进而提出了一种建立具有固定双面约束多点摩擦的多体系统动力学方程的方法。白争锋等[63]针对工程中常见的柔性多体系统碰撞过程,详细分析了系统接触碰撞条件,并基于非线性等效弹簧阻尼碰撞模型和库仑摩擦模型建立了含接触碰撞的柔性多体系统动力学模型。芮筱亭、戎保等[64-68]应用模态方法或有限元法描述柔体变形,建立了大运动柔体元件的动力学方程,推导了柔体元件全新的传递方程和传递矩阵,将多体系统离散时间传递矩阵法推广应用于一般柔性多体系统动力学的高效快速计算。谢向荣等[69]将柔性多体动力学理论应用于非线性隔振系统建模,推导出了对舰船机械设备隔振系统动力学模型。
风格迥异的现行多体系统动力学建模方法极大地推动了现代工程技术的发展,为解决各种复杂机械系统动力学问题提供了多种有效的计算手段。一般来说,已有多体系统动力学建模方法主要基于以下几类基本原理和方法[31,36,70-72]:Newton-Euler 向量力学方法、d'Alembert原理(或Jourdain原理、Lagrange方法)出发导出的分析力学方法、基于Gauss原理等极小值性质的极值原理以及传递矩阵方法等。向量力学方法建模过程中需对每个物体作隔离体分析,存在约束力,动力学方程推导过程简单,所得方程较短且比较简洁,但方程数目较多。根据采用不同的拓扑结构分析方法消除约束力的方式不同,向量力学方法形成了以不同学者命名的不同方法,如:基于图论的Roberson-Wittenburg方法、Margulies-Hooker方法、信息流图法以及矢量网络法等[5]。分析力学方法将系统作为整体考虑,在建模过程中不出现约束反力。动力学方程推导规范,方程数目少,但推导过程繁冗。基于极值原理的动力学建模方法不必建立运动微分方程,可直接应用优化计算方法进行动力学分析。基于传递矩阵法的多体系统离散时间传递矩阵法[28,31,64,65]把复杂的多体系统“分割”成若干个元件,将各元件的力学特性用矩阵表示,进而“拼装”各元件的传递矩阵获得系统总传递方程和总传递矩阵。该方法无需系统的总体动力学方程,免去了复杂繁琐的多体系统总体动力学方程的建立过程,涉及的系统矩阵阶次不取决于系统的自由度数,程式化程度高,大幅度提高了复杂机械系统的计算效率。时至今日,柔性多体系统动力学已成为当今计算多体系统动力学领域的主要研究方向,并在一系列重大工程问题中得以应用[59-61,69,73-78]。
2 多体系统动力学数值求解技术
基于不同建模方法得到的多体系统动力学方程形式不尽相同,多数情况下可表示为微分/代数方程组、非线性微分方程组[5]或关于系统边界状态矢量的总传递方程[28,31]。不同形式的多体系统动力学方程尽管在理论上具有等价性,但其数值性态的优劣不尽相同。国内外针对多体系统不同的建模方法,产生了多种多样的数值求解手段。王琪[79]、Wasfy[1]、Schiehlen[2]、王国平[5]分别对多体系统的各种计算策略进行了详细地概括与总结。
2.1 多体系统动力学微分方程求解
多体系统动力学微分方程组可表示为:

多体系统动力学二阶微分方程的数值解法通常有两条途径:直接积分法和降为一阶微分方程组后再作数值求解。由于柔性多体系统动力学方程是含有刚性运动慢变分量和变形运动快变分量的强非线性刚弹耦合的刚性方程。常用的显式积分法大都是条件稳定的,不适于求解此类方程;目前刚性常微分方程初值问题数值解法大多数是隐式算法,常见的时间积分方法有Wilson-θ法、Houbot法、直接积分法、Park刚性稳定法、Newmark法、Runge-Kuta法、Adams-Moulton隐式多步法、Taylor展开式以及 Gear法等[1-5]。隐式积分法虽存在绝对稳定的积分格式,但也潜在着计算危险性。
近年来,国内外众多学者分别从不同角度提出了一系列刚性常微分方程的高精度数值解法。钟万勰教授等提出了一种全新的可以用于求解刚性方程的绝对稳定显式精细时程积分法[80]。基于该方法,吕和祥等[81,82]提出了逐步积分法,借助线性动力学方程齐次解的解析表达式,构造了适用于强非线性、非保守动力学系统的积分方程。刘铁林等[83]提出了一种基于最小转换能原理的结构动力响应无条件稳定逐步积分算法。蒲军平[84]采用一种高阶精度的时间步积分求积方法,对双质点系及梁在强迫力作用下的振动特性进行了数值分析。Oghbaei[85]采用时间有限段隐式积分法对多体系统动力学方程数值计算进行了分析。Rill[86]提出了修正的隐式Euler算法以求解车辆动力学问题。
2.2 多体系统动力学微分/代数方程求解
多体系统动力学微分-代数方程组可表示为:
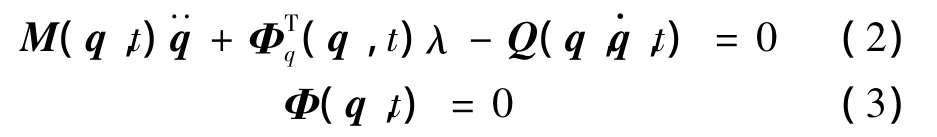
微分/代数方程的数值求解还处于不断探索和发展阶段。近20年来,国内外对微分/代数方程的数值解法进行了大量研究。根据对位置坐标阵和拉格朗日乘子处理技术的不同,其研究方法大体主要有基于增广法的直接积分法、Baumgarte违约修正法、Bayo罚函数法、超定微分/代数方程组法和基于缩并法的广义坐标分块法、QR分解法、SVD分解法、零空间法、局部参数化法等[1-5,26,36]。增广法通过选择修正系数将微分/代数方程化为微分方程来求解。修正系数的选择没有通用方法,人为凭经验选取修正系数是造成该类方法数值计算稳定性问题的主要原因。缩并法通过缩并非独立的广义坐标使方程化为纯微分方程来求解,它的数值稳定性较好,但缩并过程将大大影响计算效率。目前,在柔性多体系统动力学计算中,两种方法都有应用,哪种方法更好还没有统一的认识。
潘振宽等[87]提出了位移约束方程、速度约束方程同时自动修正方法。洪嘉振等[88]提出了受约束多体系统广义坐标主动校正方法。王琪[89,90]分别提出了树形多体系统和带约束多体系统动力学方程的隐式算法。原亮明、刘金朝等[91]将时间按照Newmark差分格式进行离散化,位移约束方程按照泰勒级数展开,给出了求解微分/代数方程的无须进行违约修正的拉格朗日乘子方法。吴国荣等[92]针对刚性微分/代数方程,基于控制方程及约束方程的泰勒展开推导出了对位移及拉格朗日乘子进行修正的 Newton-Raphson迭代公式。Betsch、Uhlar[93]提出了动能守恒积分策略,提高了数值积分的稳定性。姚廷强、迟毅林等[94]结合隐式数值积分解耦法,提出了柔性多体系统动力学的新型广义-α数值分析方法,减小了系统雅可比矩阵函数的估计数目和 Newton-Raphson迭代次数。吴洪涛等[95]提出了求解大型微分/代数方程的线性多步积分算法,提高了系统的求解效率。时至今日,微分/代数方程的求解仍是多体系统动力学的一个难点,目前仍无非常通用和程式化的方法,其发展趋势是校正方法应自动进行,不需人工干预,且违约校正不能以破坏系统动力学方程为代价[5]。
2.3 多体系统离散时间传递矩阵法求解
随着高速轻质机器人、航天器、车辆等现代机械系统构型复杂性的提高,动力学方程(1)-(3)的阶次不断增加,如何提高多体系统动力学数值计算的效率是多体系统动力学领域所面临的重要研究课题之一[1-5]。针对上述问题,芮筱亭等提出了基于传递矩阵法的多体系统离散时间传递矩阵法[28,31,64,65]。该方法采用逐步时间积分法和线性化方法线性化元件的动力学方程,获得系统中任一元件j的传递方程和传递矩阵:
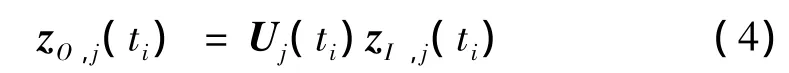
拼装各元件的传递方程可得关于系统边界状态矢量的总传递方程为:
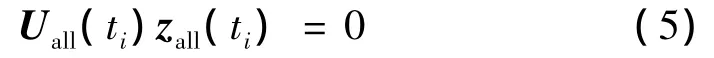
式中,zI,j和 zO,j分别为元件 j输入、输出端的状态矢量,Uj为元件j的传递矩阵,Uall和zall分别为系统总传递矩阵和系统边界状态矢量。
应用边界条件,求解系统总传递方程(5),可得ti时刻边界状态矢量zall(ti);应用元件传递方程(4),求ti时刻系统各联接点的状态矢量,得到系统在ti时刻的运动;令i=i+1,重复上述过程,直至计算到所要求的时刻T,便得到系统运动的时间历程。
应用多体系统离散时间传递矩阵法所得的系统总传递矩阵Uall的阶次与系统的自由度无关,因而可大幅度提高系统动力学的计算效率。此外,系统总传递方程为代数方程,简化了数值求解算法。
2.4 多体系统动力学方程求解策略改进
为提高多体系统建模和计算的速度,提高动力学方程的数值计算精度和稳定性,近年来出现了一系列改进的计算策略,如:显式-隐式混合求解、递归求解、多时间步长方法、并行计算策略、面向对象策略、计算机化符号推导、自适应近似策略、辛算法等[1-5]。
Martin Arnold[96]、廖建成[97,98]将多时间步长方法应用于复杂多体系统动力学分析。王波兴等[99]研究了多体动力学子系统求解算法,提高了复杂多体系统动力学求解效率。洪嘉振等[37]提出了多体系统动力学的单向递推组集建模方法,提高了多体系统动力学的计算效率、精度和稳定性。Lim等[100]针对柔性多体系统动力学方程,提出对柔体的弹性变形分量采用显式算法、刚体运动分量采用隐式算法、刚柔耦合界面处的节点采用显式-隐式混合算法的数值处理模式。Shi[101]实现了空间Euler-Bernoulli梁的符号建模计算。戈新生等[102]提出了基于完全笛卡尔坐标的多体系统微分/代数方程符号线性化方法。Perkins等[103]采用自适应技术对轨道车辆的振动进行了研究。王桥医等[104]把多体系统动力学方程中描述刚体运动的慢变自由度和弹性体变形的快变自由度分别处理,将吉尔法和显式脉冲法相结合进行数值求解,降低了时耗和所需计算机存贮。吴永等[105]建立了约束多体系统动力学微分/代数形式的约束正则方程,利用Runge-Kutta法合成辛算法对约束多体系统的约束哈密顿形式的方程进行了高稳定性仿真。吴永[106]、黄永安[107]分别概括了辛算法在多体系统动力学数值计算中的应用。洪嘉振等[108,109]阐述了多体系统动力学数值求解和动画计算与输出的并行处理算法。上述计算方法的出现为多体系统动力学高效仿真提供了有力的工具。
3 多体系统控制设计
随着国民经济和国防技术的发展,机械系统构型越来越复杂,表现为这些系统在构型上向多回路和带控制系统方向发展,系统的研制通常需要解决很多复杂系统的运动学、动力学与控制等问题,对受控多体系统动力学性能的快速准确评估和控制设计已越发凸显出其重要意义。例如,数控机床、机器人、航天器、导弹及其发射系统等众多国民经济和国防领域中的重大工程产品都是带有控制系统的机械系统。Wasfy[1]和Schiehlen[2]指出现代机械系统与控制系统结合越来越紧密,机械系统动力学与控制由于在精密机械、车辆和人造空间结构等工程技术领域中的应用而成为目前非常活跃的研究领域。近年来,有关受控机械系统动力学建模与控制设计的文献层出不穷[110-116]。对复杂受控机械系统运动学、动力学的性能分析、设计与优化已成为新的挑战性研究课题。
一般而言,现代复杂机械产品所带有的控制系统是人们为完成一定的控制任务按照预定目的、要求和性能指标而设计制造的。通常,控制系统由控制器、受控对象、反馈测量装置及比较器等部分组成。为了设计性能优良的控制系统,首先必须充分了解受控对象、测量元件、执行机构和构成控制系统的其他元器件的特性及其运动规律。对于一个实际受控多体系统,不论是进行分析还是设计,首要任务是建立受控对象的物理模型和数学模型。描述系统的数学模型,不仅应该能从本质上完全反映实际系统的特性,而且还应能从根本上确定解决系统工程问题的途径和方法。当前,受控机械系统数学模型的建立绝大多数基于第1节所述多体系统动力学方法建立系统动力学方程,进而按照现代控制理论设计适当的控制策略。
近年来,以航天器或机械臂等受控多体系统为背景,基于现代控制理论提出了各种控制方案。常用的控制方案包括动态规划理论、极大值原理、最优控制理论、鲁棒控制、自适应控制、滑模变结构控制、模糊控制、智能控制等。陆佑方[36]讨论了计算力矩方法、变结构控制理论在柔性臂系统轨迹控制中的应用。赵宏伟[117]对宏/微双重驱动机器人柔性手臂实验系统及控制策略进行了相应研究。Gangbing[118]提出将正位置反馈控制运用到柔性航天器振动控制中,并通过单轴回转装置实验验证了其良好效果。Wasfy[1]详细综述了多体系统控制设计相关文献,分别对控制系统作动器/传感器的选择和控制律的设计方法给出了具体论述,指出了柔性多体系统控制设计时存在的主要困难。Ebrahimi[119]将柔性航天器建模为线性欠阻尼弹性系统,将bang-bang控制问题转化为参数优化问题,降低了柔性附件的耦合诱发振动。Sun[112]基于线速度反馈策略实现了对单臂机械操纵器的振动主动控制。魏燕定等[120]构造了压电模态观测器,实现了对压电悬臂梁的振动控制。蔡国平等[121,122]在推导Hub-beam构型柔性多体系统一次近似耦合非线性模型基础上,针对近似线性化后的状态空间模型设计了最优控制律,在考虑时滞影响的基础上设计了时滞最优跟踪控制器。胡庆雷[123]针对扰性航天器动力学模型存在不确定性因素以及外部扰动作用的情况,将变结构输出反馈控制应用于挠性航天器的大角度机动控制。Vasques[110]采用最优反馈控制研究了智能压电梁的振动主动控制问题。Sarraf[124]设计了自组织模糊神经结构在线学习控制器,实现了单机械臂末端跟踪控制。陈龙[125]提出了不确定性受控系统保成本鲁棒PID控制策略[125]。张国庆[126]对柔性多体系统控制设计进行了深入阐述。Kim[114]、李洋[127]基于自适应控制策略,分别实现了柔性机械臂系统和挠性航天器的自适应控制。芮筱亭等[128-130]应用多体系统传递矩阵法实现了对受控多体系统动力学问题的快速建模与分析。目前,多体系统控制设计,特别是柔性多体系统控制设计,已成为国内外本领域前沿性研究课题之一。
4 多体系统动力学仿真软件开发
多体系统动力学作为研究复杂机械系统动态特性的应用基础学科,最终目的是编制通用仿真软件为工程技术领域提供强有力的计算机辅助分析工具。20世纪80年代以来,国外开发出了许多著名的多体系统商业软件包,比较知名的有 ADAMS、DADS、MADYMO、SIMPACK、DYMAC、PLEXUS、SPACAR 等。Schiehlen[12]、陆佑方[36]在专著中分别对全球大型通用仿真软件的研制和开发情况进行了详细介绍,其中的许多软件已具有对柔性多体系统进行动力学仿真的功能。随着多体系统理论和仿真算法的不断发展,上述软件的分析功能在不断增强,版本也在不断升级,大量新兴多体系统仿真软件也不断出现,如:Choi和Bae等开发了基于递归算法的新一代多体系统动力学仿真软件RecurDyn(Recursive Dynamic),其适合于求解大规模及复杂接触的多体系统动力学问题。
国内的一些大学和研究所也在多体系统动力学软件开发方面作了许多有益的尝试和研究。清华大学针对智能机器人研究,开发了THROBSM大型机器人仿真系统,可分别对单、双机械手运动学、轨迹规划、动力学及各种控制方法进行仿真。洪嘉振等根据多体系统动力学单向递推组集建模理论开发了柔性多体系统动力学通用计算机辅助分析软件 CADAMB[37,108,109]。芮筱亭等基于多体系统传递矩阵法研制开发多体系统动力学快速可视化仿真软件,用以实现对时变非线性一般受控机械系统的快速建模与仿真[131]。王建明等基于凯恩-休斯顿方法,开发了能够对任意拓扑结构的多体系统运动学和动力学进行正、逆问题分析的多体系统分析软件MBSA[132]。吴洪涛等基于空间算子代数理论,主持编制了机械系统计算动力学程序MBSSOA[133]。吉林工业大学以R-W方法为理论依据,开发了汽车碰撞计算机仿真软件SVC3D。王树新、刘又午等通过Huston提出的低序体阵列来描述和建立多体系统数学模型,开发了多体系统动力学可视化仿真软件MDAS[134]。总体而言,我国的多体系统动力学可视化仿真系统开发还处于起步阶段,难以完成国外软件的多种功能,在软件产业化方面与国外相比还存在很大的差距。
5 多体系统动力学实验研究
多体系统动力学实验研究始于20世纪70年代,其对检验多体系统理论模型的正确性、评价控制系统设计的合理性等具有重要作用。Wasfy[1]、洪嘉振[135]分别对多体系统动力学实验研究进行了详细地概括与总结。一般而言,多体系统动力学实验研究主要针对如下三类问题[135]:① 为检验某种理论方法的正确性和有效性而进行的理论模型的验证实验;②用于研究诸如系统模态频率、振型等动力学特性的多体系统动力学特性实验;③多体系统动力学控制与碰撞实验等。
杨辉、洪嘉振等[136]针对中心刚体、柔性梁和末端质量组成的刚柔耦合系统,利用单轴气浮台动力学实验平台,检验了一次近似刚柔耦合动力学模型的可行性。王树新等[137]以工业机器人为例验证了基于Kane方程的受控多体系统动力学建模的可行性。芮筱亭等[31]针对复杂武器系统建立了基于多体系统离散时间传递矩阵法的多体系统发射动力学理论,研制了弹丸起始扰动光学杠杆测试装置和复杂武器系统模态实验及其参数识别方法,验证了多体系统传递矩阵法的正确性和可行性。饶柱石等[138]对某4000HP燃气轮机组合式特种转子进行了振动模态的实验研究,探讨了传递矩阵法在转子系统振动计算中的应用。杨辉、洪嘉振等[139]从理论和实验两方面研究了由中心刚体和柔性梁组成的刚柔耦合系统的模态特性。Nakanishi等[140]对刚柔有轨车辆动力学进行了实验研究。Kwak等[141]介绍了自行研制的用于柔性多体系统动力学建模理论和控制方法对比的试验平台PACE。阎绍泽、刘才山等[142]利用柔性机械臂主动控制实验装置以及相应的动力学参数测试系统,对柔性机械臂结构-控制耦合特性进行了研究。魏井君、邱志成[143]建立了压电智能挠性悬臂梁的实验平台,采用修正Fuzzy-PI双模控制方法对悬臂梁振动进行了实验研究。陈龙祥、蔡国平[144]研究了交流伺服电机和压电激励器存在不同时滞量时,旋转运动柔性梁的时滞反馈控制的可行性和有效性。刘锦阳等[145]研究了柔性多体系统多点接触碰撞建模理论和多点接触碰撞实验方法,实验验证了非线性弹簧-阻尼碰撞力模型在柔性多体系统多点接触中的适用性。
总体而言,与众多形形色色的多体系统动力学建模理论相比,多体系统动力学实验研究还是一个较为薄弱的环节,尚不完善[135]。研制新的实验测试设备、建立适宜于不同多体系统动力学问题的实验测试方法、进一步验证现有多体系统动力学理论、探索未知的多体系统动力学现象等仍将是多体系统实验研究需要进一步努力的工作。
6 结论
本文对近年来国内外多体系统动力学建模方法、求解策略、控制设计、软件开发、实验研究等方面的研究现状进行了较为全面地概括和总结。作为当今力学领域的研究热点和难点之一,多体系统动力学是机械、航空、航天、兵器、机器人领域中大量机械系统的动态性能评估和优化设计的理论工具与技术基础,对其全面系统地研究方兴未艾,还有大量工作有待开展。下述问题将会成为多体系统动力学有待考虑的发展趋势:
(1)考虑几何非线性、材料非线性以及含复合材料的柔性多体系统动力学建模与控制设计问题。随着高速轻质机器人、航天器、车辆等复杂机械系统的高性能、高精度设计要求,大型化、低刚度与柔性化已成为航空航天、车辆、机器人及精密机械等领域的重要发展趋势。各种新型复合材料重量轻、强度和刚度大、耐高温和安全性好,在工程界被广泛使用。与传统各项同性材料相比,复合材料具有明显的非均匀性和各向异性性质[56]。上述原因导致现代机械系统柔性构件往往呈现几何非线性、材料非线性等特点。如何建立合理完备的考虑几何非线性、材料非线性的柔性多体系统动力学理论,实现对该类多体系统高效精确的控制设计已成为现代工程技术领域值得考虑的难题。
(2)不确定性多体系统动力学建模、控制与高效数值求解问题。在实际的工程问题中由于制造、测量误差及施工水平和条件限制等因素,导致了诸如系统几何参数、材料性能参数、边界条件、初始条件以及外载荷等存在着许多不确定因素。传统的确定性模型将无法反映出系统的随机性对其动态特性和控制性能的影响,甚至在某些情况下会造成系统的不稳定。如何建立高效、便捷的不确定性多体系统动力学建模与控制新方法,科学评估系统不确定性对系统动态特性和控制性能的影响,已成为实际工程技术领域不得不面对的问题。
(3)多体系统动力学与电、热、磁和流体等其他类型的物理场多场耦合问题。耦合系统是兵器、航空航天、车辆等重大工程领域常见的工程模型。上述系统一般可处理为多体子系统和电、热、磁、流体等其他子系统的耦合系统。不同子系统间的交互作用,使得整个耦合系统高度非线性,动力学行为十分复杂。另外,由于耦合系统通常具有不同的数值特性和不同的时间尺度,耦合系统数值计算的效率、精度和稳定性往往受到严峻考验。随着对耦合系统的高性能、高精度设计要求以及实时仿真和控制的需要,对耦合系统高效数值求解方法的研究,包括:系统动力学方程的建立以及提高方程求解的速度、精度和稳定性等,已越发凸显出其重要意义。
(4)多体系统刚性微分方程或微分/代数方程数值求解的稳定性和高效率依然是一块硬骨头,仍需进一步研究。
(5)加强多体系统动力学实验研究,为理论分析和数值模拟提供必要的实验支撑。目前,多体系统动力学实验研究还不能满足人们的要求。如何建立完备合理的多体系统动力学与控制问题的实验测试方法与手段,科学评价多体系统动力学理论与数值计算方法,仍将是多体系统动力学有待考虑的问题。
[1] Wasfy Tamer M,Noor Ahmed K.Computational strategies for flexible multibody systems[J] .Appl Mech Rev,2003,56(6):553-613.
[2] Schiehlen W. Computational dynamics:theory and applications of multibody systems[J] .European Journal of Mechanics A/Solids,2006,25:566 -594.
[3] Yoo W S,Kim K N,Kim H W,et al.Developments of multibody system dynamics:computer simulations and experiments[J] .Multibody Syst Dyn,2007,18:35 -58.
[4] 刘铸永,洪嘉振.柔性多体系统动力学研究现状与展望[J] .计算力学学报,2008,25(4):411-416.
[5] 王国平.多体系统动力学数值解法[J] .计算机仿真,2006,23(12):86-89.
[6] Magnus K.Dynamics of multibody systems[M] .Springer-Verlag,Berlin,1978
[7] Arczewski K,Fraczek J,Wojtyra M.Proceedings of the ECCOMASthematic conference on multibody dynamics 2009.Warsaw,Poland.
[8] Ambrósio J,et.al.Proceedings of the 7th EUROMECH solid mechanics conference[J] .Lisbon,Portugal,2009.
[9] Denier J,Finn M D,et al.Proceedings of the XXII international congress theoretical and applied mechanics[C] .Adelaide,Australia,2008.
[10] Wittenburg J.Dynamics of systems of rigid bodies[M] .Stuttgart:B.G.Teubner,1977.
[11] Kane T R,Likins P W,Levinson D A.Spacecraft dynamics[M] .New York:Mc Graw-Hill Book Company,1983.
[12] Schiehlen W.Multibody systems handbook[M] .Berlin:Springer-Verlag,1990.
[13] Nikravesh P E. Computer-aided analysis of mechanical systems[M] .Prentice-Hall,Engelwood Cliffs,NJ,1988.
[14] Roberson R E,Schwertassek R.Dynamics of multibody systems[M] .Springer-Verlag,Berlin,1988.
[15] Haug E J.Computer-aided kinematics and dynamics of mechanical systems[M] .Allyn and Bacon,Boston,1989.
[16] 贾书惠.刚体动力学[M] .北京:高等教育出版社,1986.
[17] 刘延柱,洪嘉振,杨海兴.多刚体系统动力学[M] .北京:高等教育出版社,1989.
[18] 休斯敦,刘又午.多体系统动力学[M] (上册).天津:天津大学出版社,1987.
[19] 休斯敦,刘又午.多体系统动力学[M] (下册).天津:天津大学出版社,1991.
[20] 袁士杰,吕哲勤.多刚体系统动力学[M] .北京:北京理工大学出版社,1992.
[21] 陈乐生,王以轮.多刚体动力学基础[M] .哈尔滨:哈尔滨工程大学出版社,1993.
[22] Shabana A A.Computational dynamics[M] .Wiley,New York,1994.
[23] De Jalon G J,Bayo E.Kinematic and dynamic simulation of multibody systems:The real time challenge[M] .New York:Springer-Verlag.1994.
[24] Stejskal V, Valasek M. Kinematics and dynamics of machinery.Marcel dekker[M] .New York,1996.
[25] 姚文莉,陈 滨.考虑摩擦的平面多刚体系统的冲击问题[J] .北京大学学报(自然科学版),2004,40(5):729-734.
[26] 陈立平,张云清,任卫群,等.机械系统动力学分析及ADAMS应用教程[M] .北京:清华大学出版社,2005.
[27] Rui X T,Lu Y Q,Ling P,et al.Discrete time transfer matrix method for mutibody system dynamics,in Euromech colloquium 404 on advances in computational multibody dynamics[C] .Lisbon,Portugal,1999,93 -108.
[28] Rui X T,He B,Lu Y Q,et al.Discrete time transfer matrix method for multibody system dynamics[J] .Multibody System Dynamics,2005,14(3-4),317-344.
[29] Wittenburg J.Dynamics of multibody systems[M] .Springer,Ber Lin,2008.
[30] Featherstone R. Rigid body dynamics algoriths[M] .Springer,New York,2008.
[31] 芮筱亭,贠来峰,陆毓琪,等.多体系统传递矩阵法及其应用[M] .北京:科学出版社,2008.
[32] Shabana A A.Dynamics of multibody systems,3rd edition.Cambridge university press[M] .New York,2005.
[33] Huston.Multibody dynamics[M] .Boston:Butterworth-Heinemann,1990.
[34] Bremer H,Pfeiffer F.Elastische mehrkorpersystem[M] .Teubner,Stuttgart,1992.
[35] 黄文虎,邵成勋.多柔体系统动力学[M] .北京:科学出版社,1996.
[36] 陆佑方.柔性多体系统动力学[M] .北京:高等教育出版社,1996.
[37] 洪嘉振.计算多体系统动力学[M] .北京:高等教育出版社,1999.
[38] 覃 正.多体系统动力学压缩建模[M] .北京:科学出版社,2000.
[39] Geradin M,Cardona A.Flexible multibody dynamics-A finite element approach[M] .New York:Wiley,2001.
[40] 彼得·艾伯哈特,胡 斌.现代接触动力学[M] .南京:东南大学出版社,2003.
[41] Ambrósio J A C,Gon.alves Jo.o P C,Complex flexible multibody systems with application to vehicle dynamics[J] .Multibody System Dynamics,2001,10(6):168 -182.
[42] Goncalves Jo O PC.Rigid and flexible multibody systems optimization for vehicle dynamics[D] .Ph.D.dissertation,Instituto Superior Técnico of the Technical University of Lisbon,2002.
[43] Ambrósio Jorge A C, Neto Maria A, Leal Rogério P.Optimization of acomplex flexible multibody systems with composite materials[J] .Multibody Syst Dyn 2007,18:117-144.
[44] 潘振宽,丁洁玉,高 磊,等.多体系统动力学动态最优化设计与灵敏度分析.力学学报,2005,37(5):612-619.
[45] Wasfy T M,Noor A K.Finite element analysis of flexible multibody systems with fuzzy parameters[J] . Comput.Methods Appl.Mech.Engrg.1998,160:223 -243
[46] Sandu A.Sandu C.Ahmadian M.Modeling multibody systems with uncertainties.Part I:Theoretical and computational aspects[J] .Multibody Syst Dyn 2006,15:373 -395.
[47] Wittbrodt E,Wojciech S.Dynamics of flexible multibody systems:rigid finite element method[M] .Springer-Verlag Berlin Heidelberg,2006.
[48] Michael Lehner,Peter Eberhard.A two-step approach for model reduction in flexible multibody dynamics[J] .Multibody Syst Dyn,2007,17:157-176.
[49] 齐朝晖.多体系统动力学[M] .北京:科学出版社,2008.
[50] 齐朝晖,许永生,罗晓明.含非理想约束多柔体系统递推建模方法[J] .力学学报,2008,40(5):686-694.
[51] Yoo W S,Lee J H,Park S J,et al.Large Deflection Analysis of a Thin Plate:Computer Simulations and Experiments[J] .Multibody System Dynamics,2004,11:185-208.
[52] Yoo W S,Lee J H,Park S J,et al.Large Oscillations of a Thin Cantilever Beam:Physical Experiments and Simulation Using the Absolute Nodal Coordinate Formulation[J] .Nonlinear Dynamics,2003,34:3 -29.
[53] 李 彬,刘锦阳.大变形柔性梁系统的绝对坐标方法[J] .上海交通大学学报,2005,39(5):828-831.
[54] Laith K.Abbas.Computational Studies on Flexible Multibody System Dynamics and Aeroelasticity[R] .南京理工大学博士后研究工作报告,2009.
[55] 田 强.基于绝对节点坐标方法的柔性多体系统动力学研究与应用[D] .武汉:华中科技大学,2009.
[56] 刘锦阳,潘科琪.考虑热效应的复合材料多体系统动力学研究[J] .动力学与控制学报,2009,7(1):9-13.
[57] 王中双,陆念力.基于键合图的多体系统耦合动力学的发展及现状[J] .中国机械工程,2007,18(17):2137-2141.
[58] 方喜峰,吴洪涛,刘云平,等.基于空间算子代数理论计算多体系统动力学建模[J] .机械工程学报,2009,45(1):228-234.
[59] 蒋建平,李东旭.带太阳帆板航天器刚柔耦合动力学研究[J] .航空学报,2006,27(3):418-422.
[60] 刘又午,王建明,刘才山,等.作大范围运动的空间桁架结构动力分析[J] .振动工程学报,1998,11(1):18-23.
[61] 何柏岩,王树新,金国光.计及参数不确定性的卫星太阳能帆板的柔性多体动力学研究[J] .自然科学进展,2003,13(4):434-438.
[62] 彭慧莲,王士敏,王 琪,等.双面约束多点摩擦多体系统的建模和数值方法[J] .力学学报,2009,41(1):105-112.
[63] 白争锋,赵 阳,田 浩.柔性多体系统碰撞动力学研究[J] .振动与冲击,2009,28(6):75-78.
[64] Rui X T,He B,Rong B,et al.Discrete time transfer matrix method for multi-rigid-flexible-body system moving in plane[J] .Proc.Inst.Mech.Eng.Part K J.Multi-body Dyn.,2009,223(K1):23-42.
[65] Rong B,Rui X T,Wang G P.New method for dynamics modelling and analysis on flexible plate undergoing large overall motion[J] .Proc.Inst.Mech.Eng.Part K J.Multibody Dyn.,2010,224(K1):33 -44.
[66] Rong B,Rui X T,Wang GP,et al.New efficient method for dynamics modeling and simulation of flexible multibody systems moving in plane[J] .Multibody Syst.Dyn.,2010,24(2),in press.
[67] Rong B,Rui X T,Wang G P.Dynamics modelling and simulation of spacecraft with flexible solar panel[C] .International Conference on Mechanical Engineering and Mechanics 2009,Beijing,China.
[68] Rui X T,Rong B,He B,et al.Discrete time transfer matrix method of multi-rigid-flexible-body system(keynote)[C] .International Conference on Mechanical Engineering and Mechanics 2007.Science Press USA Inc,2244 -2250.
[69] 谢向荣,俞 翔,朱石坚.基于柔性多体系统动力学理论的舰船机械设备隔振系统建模[J] .振动与冲击,2009,28(9):200-203.
[70] Schiehlen W,Nils G,Robert S.Multibody dynamics in computational mechanics and engineering applications[J] .Computer Methods in Applied Mechanics and Engineering,2006,195:5509-5522.
[71] Schiehlen W.Research trends in multibody system dynamics[J] .Multibody System Dynamics,2007,18(1):3-13.
[72] Schiehlen W. Multibody system dynamics:roots and perspectives[J] .Multibody Syst.Dyn.1997,1:149 - 188.
[73] 芮筱亭,陆毓琪,王国平,等.多管火箭发射动力学仿真与试验测试方法[M] .北京:国防工业出版社,2003.
[74] 芮筱亭,等.多体系统发射动力学[M] .北京:国防工业出版社,1995.
[75] 何 斌,芮筱亭,贠来峰,等.自行火炮固有频率相关性分析的 Monte Carlo传递矩阵法[J] .振动与冲击,2008,27(11):83-86.
[76] 芮筱亭,王国平,贠来峰,等.某远程多管火箭振动特性研究[J] .振动与冲击,2005,24(1):8-12.
[77] 马 蕾,芮筱亭,杨富锋,等.激光陀螺捷联惯导减振系统建模与动力学分析[J] .振动工程学报,2009,22(6):603-607.
[78] Rong B,Rui X T,Wang G,et al.Discrete time transfer matrix method for dynamic modeling of complex spacecraft with flexible appendages[J] .Journal of Computational and Nonlinear Dynamics,2010,in press.
[79] 王 琪,陆启韶.多体系统Lagrange方程数值算法的研究进展[J] .力学进展,2001,31(1):9-17.
[80] 钟万勰.暂态历程的精细计算方法[J] .计算结构力学及其应用,1995,12(1):1-6.
[81] 吕和祥,于洪洁,裘春航.动力学方程的解析逐步积分法[J] .工程力学,2001,18(5):1-7.
[82] 吕和祥,于洪洁,裘春航.动力学方程的积分型直接积分法[J] .应用数学和力学,2001,22(2):151-156.
[83] 刘铁林,刘钧玉.基于最小转换能原理的一种逐步积分法[J] .工程力学,2005,22(2):1-24.
[84] 蒲军平.基于一种高精度微分求积法的结构动力响应数值计算[J] .南京航空航天大学学报,2004,36(3):151-156.
[85] Oghbaei M,Anderson K S,A new time-finite-element implicit integration scheme for multibody system dynamics simulation[J] .Comput.Methods Appl.Mech.Engrg,2006,195:7006-7019.
[86] Rill G.A Modified Implicit Euler Algorithm for Solving Vehicle Dynamic Equations[J] . Multibody System Dynamics,2006,15:1-24.
[87] 潘振宽.多体系统动力学微分/代数方程位置、速度约束违约自动修正方法[C] .多体系统动力学与控制,北京:北京理工大学出版社,1996,31-35.
[88] 于 清,洪嘉振.受约束多体系统一种新的违约校正方法[J] .力学学报,1998,30(3):300-306.
[89] 王 琪,黄克累,陆启韶.树形多体系统动力学的隐式数值算法[J] .力学学报,1996,28(6):717-725.
[90] 王 琪,黄克累,陆启韶.带约束多体系统动力学方程的隐式算法[J] .计算力学学报,1999,16(4):410-415.
[91] 原亮明,王成国,刘金朝,等.一种求解多体系统微分-代数方程的拉格朗日乘子方法[J] .中国铁道科学,2001,22(2):51-54.
[92] 吴国荣,陈福全,唐瑞霖.一种求解柔性多体系统动力学方程的新方法[J] .力学季刊,2005,26(2):211-215.
[93] Betsch P,Uhlar S.Energy-momentum conserving integration of multibody dynamics[J] .Multibody Syst Dyn,2007,17:243-289.
[94] 姚廷强,迟毅林,黄亚宇.柔性多体系统动力学新型广义-α数值分析方法[J] .机械工程学报,2009,45(10):53-60.
[95] 田富洋,吴洪涛,赵大旭,等.空间柔性机器人动力学分析的快速积分算法[J] .山东大学学报(工学版),2009,39(3):94-98.
[96] Arnold M.Multi-rate time integration for large scale multibody system models[C] .IUTAM Symposium on Multiscale Problems in Multibody System Contacts,Springer,2006,1 -10.
[97] Miao J C,Zhu P,Shi G L,et al.Study on sub-cycling algorithm for flexible multi-body system-integral theory and implementation flow chart[J] .Comput Mech,2008,41:257-268.
[98] Miao J C,Zhu P,Shi G L,et al.Study on sub-cycling algorithm for flexible multi-body system:stability analysis and numerical examples[J] .Comput Mech,2008,41:269-277.
[99] 夏鸿建,王波兴,陈立平.多体系统动力学子系统求解算法[J] .计算力学学报,2009,26(1):20-25.
[100] Lim H,Taylor R L.An explicit-implicit method for flexiblerigid multibody systems[J] .Finite Elem.Anal.Design,2001,37:881-900.
[101] Shi P,Mc Phee J,Dynamics of flexible multibody systems using virtual work and linear graph theory[J] .Multibody Syst.Dyn.2000,4(4):355 -381.
[102] 戈新生,赵维加,陈立群.基于完全笛卡尔坐标的多体系统微分-代数方程符号线性化方法[J] .工程力学,2004,21(4):106-111.
[103] Ma Z D,Perkins N C.Modeling of track-wheelterrain interaction for dynamic simulation of tracked vehicles:numerical implementation and further results[C] .Proc of ASME 2001 DETC,Pittsburgh PA.2001.
[104] 王桥医,唐文评.一种求解多体系统动力学响应的有效数值方法[J] .机械设计与研究,2005,21(3):46-48.
[105] 吴 永,杜思义,胡继云,等.约束多体系统动力学方程的辛算法[J] .重庆大学学报,2004,27(6):102-105.
[106] 吴 永,胡继云,殷学纲.多体系统动力学方程在流形上的辛算法[J] .力学进展,2002,32(2):189-195.
[107] 黄永安,尹周平,邓子辰,等.多体动力学的几何积分方法研究进展[J] .力学进展,2009,39(1):44-57.
[108] 常忠正,洪嘉振.基于MPI的柔性多体系统动力学并行计算[J] .宇航学报,2006,27(1):89-93.
[109] 刘勇,洪嘉振,杨 辉.多体系统动力学求解与动画输出的并行处理[J] .力学学报,2002,34(1):131-135.
[110] Vasques C M A,Rodrigues J D.Active vibration control of smart piezoelectric beams:comparison of classical and optimal feedback control strategies[J] .Computers and Structures,2006,84:1402 -1414.
[111] Li F M,Kishimoto K,et al,Vibration control of beams with active constrained layer damping[J] .Smart Materials and Structures,2008,17:065036(9pp).
[112] Sun D,Mills J K,et al.,A PZT actuator control of a single-link flexible manipulator based on linear velocity feedback and actuator placement[J] .Mechatronics,2004,14:381-401.
[113] Shin H C,Choi S B.Position control of a two-link flexible manipulator featuring piezoelectric actuators and sensors[J] .Mechatronics,2001,11:707-729.
[114] Kim H K,Choi SB,et al.Compliant control of a two-link flexible manipulator featuring piezoelectric actuators[J] .Mechanism and Machine Theory,2001,36:411 -424.
[115] Oke G,Istefanopulos Y.Tip position control of a two-link flexible robot manipulator based on nonlinear deflection feedback[J] .Chaos,Solitons and Fractals,2003,17:499-504.
[116] Zhang X M,Shao C J,Arthur G E.Active vibration controller design and comparison study of flexible linkage mechanism systems[J] .Mechanism and Machine Theory,2002,37:985-997.
[117] 赵宏伟.宏/微双重驱动机器人柔性手臂实验系统及控制策略的研究[D] .哈尔滨:哈尔滨工业大学,2000.
[118] Gang B S,Brij N A.Vibration supp ression of flexible spacecraft during attitude control[J] .Acta Astronautica.2001,49(2):73-83.
[119] Ebrahimi A,Moosavian S A A.Minimum-time optimal control of flexible spacecraft for rotational maneuvering[C] .Proeeedings of the 2004 IEEE International Conference on Control Applications,TaiPei,Taiwan,September 2 - 4,2004:961-966.
[120] 魏燕定,陈定中,程耀东.压电悬臂梁振动的模态控制[J] .浙江大学学报 (工学版),2004,38(9):1180-1184.
[121] 滕悠优,蔡国平.柔性机械臂的时滞最优跟踪控制[J] .应用力学学报,2007,24(3):399-404.
[122] Ping C G,Lim C W.Aetive control of a flexible hub-beam system using optimal tracking control method[J] .Meehanieal Sciences,2006,48:1150 -1162.
[123] 胡庆雷.扰性航天器姿态机动的主动振动控制[D] .哈尔滨工业大学,2006.
[124] Sarraf S,Fallah A,Seyedena T.A neurofuzy controller for a single link fiexible manipulator[C] .Artifieial Neural Networks—ICANN2007, Leeture Notes in Computer Scienee,Springer,2007:621 -629.
[125] 陈 龙.不确定结构(系统)控制的性能分析与综合[D] .西安:西安电子科技大学,2008.
[126] 张国庆.柔性多体系统建模与控制[D] .合肥:中国科技大学,2008.
[127] 李 洋,仇原鹰,张 军,等.一种挠性航天器的自适应姿态控制与振动控制[J] .振动与冲击,2009,28(12):178-182.
[128] 戎 保,芮筱亭,杨富锋,等.受控柔性机械臂动力学建模仿真[J] .振动工程学报,2009,22(2):168-174.
[129] Rong B,Rui X T,Yang F,et al.Discrete time transfer matrix method for dynamics of multibody system with realtime control[J] .Journal of Sound and Vibration,2010,329(6):627-643.
[130] 陆卫杰,芮筱亭,贠来峰,等.受控线性多体系统传递矩阵法[J] .振动与冲击,2006,25(5):24 -27.
[131] 芮筱亭,王国平,戎保等.ZL200810076701.8[P] .中国发明专利,2009.
[132] 王建明,胡志刚.多体系统分析软件的开发与应用[J] .山东大学学报(工学版),2004,34(1):39-43.
[133] 孙宏丽,吴洪涛,田富洋.空间算子代数刚柔耦合系统动力学软件流程[J] .华中科技大学学报(自然科学版),2009,37(12):107-111.
[134] 王树新,员今天,杨发亮.机械多体系统动力学可视化仿真方法研究[J] .计算机辅助设计与图形学学报,2002,14(4):339-342.
[135] 杨 辉,洪嘉振,余征跃.柔性多体系统动力学实验研究综述[J] .力学进展,2004,34(2):171-181.
[136] 杨 辉,洪嘉振,余征跃.刚柔耦合建模理论的实验验证[J] .力学学报,2003,35(2):253-256.
[137] 王树新,刘又午,周大宁.受控多体系统的力约束分析与实验研究[J] .天津大学学报,1997,30(5):601-606.
[138] 饶柱石,夏松波,汪光明.组合式特种转子振动模态的实验研究与计算[J] .振动与冲击,1996,15(1):68-70.
[139] 杨 辉,洪嘉振,余征跃.一类刚-柔耦合系统的模态特性与实验研究[J] .宇航学报,2002,23(2):67-72.
[140] Nakanishi T, Isogai K. Comparison between flexible multibody tracked vehicle simulation and experiment data[C] .Paper No DETC2001/VIB - 21355,Proc of the ASME 2001 DETC,Pittsburgh PA.
[141] Kwak M K,Sehlaegel W T,Das A.PACE:a test bed for the dynamics and control of flexible multibody systems[C] .Collection of Technical Papers-AIAA/ASME Structures,Structural Dynamics and Materials Conference 34th,1993.
[142] 阎绍泽,季林红,刘才山,等.柔性机械臂结构-控制耦合特征的实验研究[J] .机械科学与技术,2000,19(5):796-799.
[143] 魏井君,邱志成,叶春德.基于模糊控制的压电挠性梁的振动主动控制实验研究[J] .振动与冲击,2008,27(12):91-96.
[144] 陈龙祥,蔡国平.旋转运动柔性梁的时滞主动控制实验研究[J] .力学学报,2008,40(4):520-527.
[145] 刘锦阳,马易志.柔性多体系统多点碰撞的理论和实验研究[J] .上海交通大学学报,2009,43(10):1667-1671.

