基于多假设检验的新型小波滤波算法
杜文辽,刘成良,李彦明
(1.上海交通大学 机械与动力工程学院,上海 200240,2.郑州轻工业学院 机电工程学院,郑州 450002)
对含有噪声的信号进行滤波处理是信号处理领域的重要课题之一。由于小波在时频域同时具有良好的局部化功能及多分辨率特性,而受到广泛的应用。小波阈值滤波中,阈值的选取直接影响滤波效果。目前,确定滤波阈值的方法主要有通用阈值法、极小化风险阈值法、多假设检验法和 Bayes Shrink阈值法[1]。Abramovich 和 Benjamini[2]指出,小波阈值处理过程可以看作是一个多重假设检验过程,通过检验小波系数是否为0,仅保留一些较显著的系数,在允许一定误判的情况下,引入 FDR[3]准则,通过step-up过程来确定小波滤波阈值。
Benjamini和Liu[4]提出了基于多假设检验FDR方法的step-down过程,并且指出在假设样本较少并有大量非真假设存在的情况下,该过程较step-up过程具有更大的势(power)。Troendle[5]进一步证明了合适选择临界常数step-up和step-down过程能够控制FDR在给定的水平。Tamhane[6]提出了多假设检验中的step-updown过程,该方法在具有最少拒绝数目先验知识的情况下非常有效。Sarker[7]证明了 step-up和 step-down过程在控制FDR本质上是一致的。
本文将step-up-down过程控制FDR的方法引入到确定小波滤波阈值的算法中,该方法不仅适于具有信号噪声先验知识的情况,而且也适于没有先验知识的情况,并能够加快阈值的确定过程。通过灵活设置显著性水平,可以得到满意的滤波效果。
1 FDR的定义
对于单个假设检验问题,设Θ是参数空间,θ为参数。θ∈Θ0代表原假设,记为H0。与H0不相容的假设称为备择假设,记为H1,这时θ∈Θ1。这里Θ0∩Θ1=Ω,Θ0∪Θ1=Θ。通常的检验策略是控制第Ⅰ类错误,即弃真错误,同时尽量减小犯第Ⅱ类错误,即取伪错误。
同时对多个假设进行检验时,情况将变得更为复杂。表1给出了m个假设检验的不同结果。这时候每个检验都可能同时存在第Ⅰ类错误和第Ⅱ类错误,如何衡量总体检验的错误率是不确定的。传统上采用family wise错误率(FWER),但在很多情况下,FWER过于保守。Benjamini和Hochberg[3]引入了一个新的准则——错误发现率(FDR)来衡量总体检验的错误率,FDR指在多重假设检验中,错误的拒绝频数与拒绝频数比值的数学期望,可以表示为:q=FDR=,在相同控制水平下,FDR控制过程较FWER控制过程拒绝更多的原假设,即FDR相对宽松,从而具有更大的势。

表1 多假设检验输出结果Tab.1 Possible outcomes from m hypothesis tests
2 Step-up和step-down过程控制FDR
Benjamini和 Hochberg[3]提出的多假设检验 FDR准则(记为 BH FDR),检验方法采用的是 Simes[8]提出的算法,其检验过程如下:参数空间Θ中各样本点为独立同分布,设 p1,p2,…,pm为检验统计量的 p值,其大小反映了显著性水平的高低,对应的原假设为H(1),H(2),…,H(m)。对p值进行排序得到序列 p(1)≤p(2)≤…≤p(m),记p(t)对应的原假设为H(i),从最大的p值p(m)开始,依次是 p(m-1),p(m-2),…,取临界常量 c(i)=(i/m)q,令 k=max{i∶p(i)≤c(i)},然后拒绝所有的H(i),i=1,2,…,k。这就是控制 FDR 显著性水平在 q的step-up过程。
Benjamini和 Liu[4]给出了一种 FDR step-down 控制过程:从最小的p值p(1)开始,依次是p(1),p(2),…,取临界常量,令k=min{i∶p(i)> c(i)},然后拒绝所有的 H(i),i=1,2,…,k。可以证明,该过程也能控制FDR在水平q,并且在m较小并且有大量非真假设存在的情况下,该过程较step-up过程具有更大的势。
3 FDR step-up-down小波阈值滤波算法
FDR多假设检验过程要求样本是独立(independent)分布的,一般时序信号并不符合FDR多假设检验过程的条件。正交小波变换具有很强的去相关特性,经过小波变换得到的小波系数可以认为是相互独立的,由于小波阈值滤波可以看作是一个多假设检验过程,得出FDR step-up-down小波滤波算法如下:
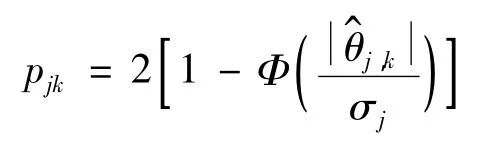
对 pj,k按从小到大排序,即 p(1)≤p(2)≤…≤p(m),每一个 pi对应的小波系数为,对应的原假设0)记为 H(1),H(2),…,H(m)。选择评价常数 0≤c(1)≤c(2)≤…≤c(m)≤1,暂取 c(i)=(i/m)q,并选取 r初始值。
(2)如果p(r)≤c(r),那么拒绝原假设H(1),H(2),…,H(r),转(4)。
(3)如果 p(r)>c(r),接受原假设,H(1),H(2),…,H(r),转(5)。
(4)令H(i)表示最后拒绝的原假设(在(2)中,i=r),如果i=m,停止并且 k=i;否则,检查 H(i+1),如果p(i+1)>c(i+1),那么接受 H(i+1),H(i+2),…,H(m)并停止并且k=i。如果p(i+1)≤c(i+1),那么拒绝H(i+1)。令i=i+1,返回(4)。这一步中 c(i)=1-[1-min(1,mq/(m
(5)令H(i)表示最后接受的原假设(在(3)中,i=r),如果 i=1,停止并且 k=i;否则,检查 H(i-1),如果p(i-1)≤c(i-1),那么拒绝 H(i-1),H(i-2),…,H(1)并停止并且 k=i。如果 p(i-1)> c(i-1),那么接受 H(i-1)。令 i=i-1,返回(5)。
(6)计算阈值,阈值就是上面得到的p(k)对应的小波系数,并对小波系数进行阈值化处理。
显然,上面算法中,如果r=m,则是step-up过程;如果r=1,则是step-down过程。当具有r的先验知识的时候,也就是如果知道大约有r0个0假设为真,则取r=r0。当没有这个先验知识的时候,可以由程序生成一个随机数 r∈[1,m] 。
在对小波系数进行阈值化处理中,常用的阈值函数有硬阈值方法和软阈值方法两种,硬阈值函数是不连续函数,会产生一些间断点,实践证明软阈值效果较好[9]。对任一小波系数 θ^j,k,软阈值函数为:

T为由FDR step-up-down方法得出的小波阈值。
4 算例
为了验证本文方法的效果,以Matlab工具箱中的典型信号heavy sine为例进行仿真实验。通过对原始信号叠加白噪声形成待处理信号,利用db5小波对信号进行5层分解,实验中采用前述软阈值方法。图1为原始信号、含噪信号及显著性水平取0.05时经FDR step-up-down滤波后的对比图。为对比不同显著性水平的影响及不同降噪方法的效果,以信噪比和最小均方误差为度量指标,表2列出了对seavy sine含噪信号分别采用BH FDR、FDR step-up-down、heursure、sqtwolog阈值滤波后的结果。其中,对BH FDR和FDR step-updown 的显著性水平分别取 0.05、0.2。
信噪比及最小均方误差采用如下公式计算[10]:

从图1可以看出,对含噪信号利用本文提出的FDR step-up-down方法滤波后,信号质量明显得到改善。从表2根据SNR、MSE计算出的结果来看,改变FDR显著性水平的大小对信号质量的改善影响也非常显著。在大部分情况下,本文所提出的方法较经典的BH FDR方法表现更佳,其性能与heursure滤波效果相当,这三种阈值都明显优于sqtwolog方法。分析表2还可以看到,FDR step-up-down方法可以根据滤波结果灵活选择显著性水平的大小,进而取得比较理想的滤波效果。由于对FDR step-up-down过程r初始值的选取是采用取随机数的方法,每执行一次滤波过程得到的SNR、MSE会有所变化,但总体上其势要大于FDR过程,并且在小波系数较多的情况下,可以明显提高算法的速度。如果已知信号中噪声点的先验知识,可以根据该先验知识确定r的初始值,从而获得较大的势。
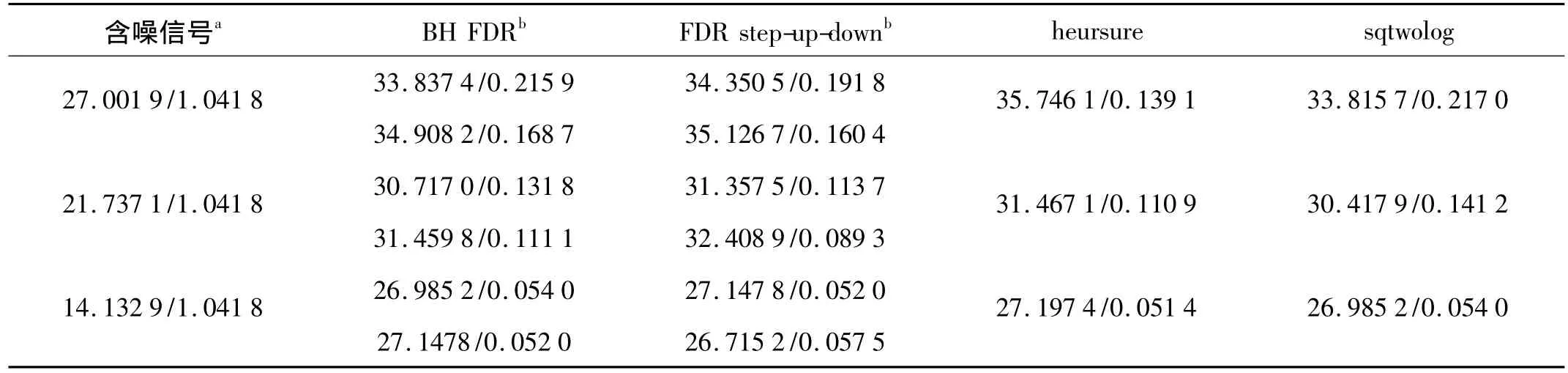
表2 heavy sine信号小波去噪前后不同阈值准则对比(SNR/MSE)SNR单位:dBTab.2 The compare of wavelet de-noising of heavy sine signal with different methods(SNR/MSE)

图1 不同信噪比heavy sine信号q=0.05时滤波效果Fig.1 The de - noising result of heavy sine signal with different SNR at q=0.05
下面用一组来自美国Case Western Reserve University电气工程实验室的滚动轴承实验数据来进行实例验证,轴承型号SKF6205,采样频率为12 kHz。图2上部分为轴承内圈损伤的振动加速度原始信号,下部分为利用本文所提方法进行小波分解重构后的信号,其中,选择db5小波,显著性水平取0.05。从图中可以看出经过滤波后信号质量有了明显改善。

图2 滚动轴承内圈故障原始数据及滤波结果Fig.2 Original signal and De-noised signal of ball bearing inner race fault

图3 不同显著性水平下得到的信噪比Fig.3 The SNR for different significant levels
为了考察采用不同显著性水平时,FDR step-updown方法对滤波效果的影响,采用前述heavy sine信号,叠加白噪声信号,形成SNR为21.7371的待处理信号。取显著性水平变化范围为0.05到0.4,步长0.01。利用db5小波对信号进行5层分解,采用前述软阈值方法进行滤波。经FDR step-up-down方法滤波后计算出对应的SNR如图3所示。从图中可以看出,FDR step-up-down滤波效果与显著性水平大小的选取关系很大,并且表现出并非简单的线性关系。分析其中存在的原因,主要是FDR step-up-down方法初始启动值的影响,另外,显著性水平反映了错误拒绝原假设的情况,但是并没有考虑到错误接受备择假设。因此,如果只选择显著性水平作为小波滤波阈值选择的依据,就必须根据经验选择合适的显著性水平,或者考虑错误接受备择假设的情况进行折中。
5 结论
本文针对小波滤波算法中阈值选取问题,构造了FDR step-up-down过程确定小波滤波阈值的新算法。在具有噪声信息先验知识的前提下,可以更有效、快捷的求得阈值,但是在通常情况下,关于噪声的先验知识比较难以获得,这时,用随机数方法产生一个初始的启动值r,也同样可以体现出算法的优越性。在算法实现过程中,可以根据滤波效果,灵活选择显著性水平的大小,这是该算法的另一个优势。仿真实验表明,显著性水平大小的选择对滤波效果有明显的影响,如何更进一步将错误接受择备假设的情况考虑进来,是下一步改进的方向。
[1] 潘 泉,张 磊,孟晋丽,等.小波滤波方法及应用[M] .北京:清华大学出版社,2005.
[2] Abramovich F,Benjamini Y. Thresholding of wavelet coefficients as multiple hypotheses testing procedure[J] .Lecture Notes in Statistics,1995,103:5 -14.
[3] Benjamini Y,Hochberg Y.Controlling the false discovery rate:a practical and powerful approach to multiple testing[J] .Journal of the Royal Statistical Society.Series B(Methodological),1995,57(1):289 -300.
[4] Benjamini Y,Liu W.A step-down multiple hypotheses testing procedure that controls the false discovery rate under independence[J] . Journal of Statistical Planning and Inference,1999,82(1 -2):163 -170.
[5] Troendle JF.Stepwise normal theory multiple test procedures controlling the false discovery rate[J] .Journal of Statistical Planning and Inference,2000,84(1 -2):139 -158.
[6] Tamhane A C,Liu W,et al.A generalized step-up-down multiple test procedure[J] .Canadian Journal of Statistics,1998,26(2):353 -363.
[7] Sarkar SK.Some results on false discovery rate in stepwise multiple testing procedures[J] .Annals of Statistics,2002,30(1):239-257.
[8] Simes R.An improved bonferroni procedure for multiple tests of significance[J] .Biometrika,1986,73(3):751 -754.
[9] Donoho D.De-noising by soft-thresholding[J] . IEEE transactions on information theory,1995,41(3):613 -627.
[10] 刘卫东,刘尚合,胡小锋,等.小波阈值去噪函数的改进方法分析[J] .高电压技术,2007,33(10):59 -63.

