分圆类在离散信号设计中的应用

孙彩锋，刘红梅，邢经纬

（1.山西大同大学物理与电子科学学院，山西大同 037009；2.燕山大学里仁学院，河北秦皇岛 066004）

分圆类在离散信号设计中的应用

孙彩锋1，刘红梅1，邢经纬2

（1.山西大同大学物理与电子科学学院，山西大同 037009；2.燕山大学里仁学院，河北秦皇岛 066004）

研究了利用分圆类构造差集偶问题。首先，基于分圆类和差集偶概念和基本性质，提出在一种分圆中用分圆类构造差集偶的两个定理，并给出证明过程和具体事例；然后，利用分圆类得到的差集偶构造出对应的最佳二元序列偶；最后，把分圆类构造的差集偶的这种数学理论应用到最佳离散信号设计中。

差集偶；分圆类；序列偶；离散信号设计

最佳离散信号设计问题不仅在通信、电子工程的设计起着极其重要的作用，而且还与许多数学学科有着密切的联系。数学领域的发展使最佳离散信号的设计［1］有更多的数学工具可用，从而极大地促进了最佳离散信号设计发展。在过去的几十年中，国内外学者经过不断地努力，成功地设计了许多类同时具有循环自相关和互相关特性的阵列（序列），同时由于具有良好循环自相关特性最佳离散信号，往往与一些著名的区组设计［2］（如差集、差集偶）具有等价关系。由于最佳二元序列偶选择范围是更广泛的最佳离散信号，且为工程应用提供了更大的信号选择空间，而差集偶和最佳二元序列偶具有等价关系。文献［3］中提出了利用差集构造差集偶，以及利用差集偶的性质可以构造出大量的差集偶。文献［4］和［5］是从软件和硬件两方面对信号设计进行了研究。基于上面的分析，本文采用了分圆类构造差集偶的新方法，并将得到的最小二进序列偶应用到最佳离散信号设计中，很好地满足了多种工程的需要。

1 定义

定义1［6］：设D，D′是v阶Abel群G的两个子集，k，k′为集合D，D′中元素的个数，即：，，e为D，D′中相同元素的个数，即：e，若G中任意非零元，在此差表中恰好出现λ次，则称（D，D′）为G上的（v，k，k′，e，λ）-差集偶，记作DSP（v，k，k′，e，λ）.

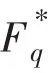
2 分圆类构造差集偶

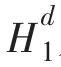
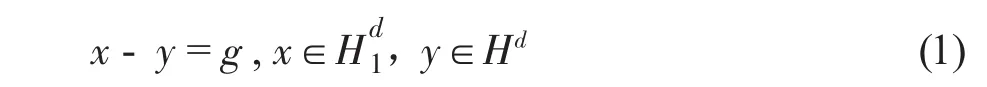
此方程的解数都是λ，由引理［6］得当g∈时方程（1）的解数为（i，1）d，故对i=0，1，都有（i，1）=λ，且λ为整数，所以由λ=f/d得f为偶数，其中d=2故得必要性。

再证充分性：设f为偶数且式（i，1）d=f/d成立，则对中的任一元素g，由定理得方程（1）的解数都是f/d，从而构成一个（q，f，k，0，f/d）—差集偶.即得结论。

100以内是奇素数并且f为偶数的有5，13，17，29，37，41，53，61，73，89，97。那么根据新提出的分圆类构造差集偶的方法，找出q为这些奇素数时Fq加法群中的差集偶，并用差集偶的定义来证明这差集偶的正确性。

例1.当q为13时，素数13的本原元是2，按照D=Hd= ｛1，w2，K，w2（f-1）｝D′＝＝ ｛w，w3，L，w2（f-1）+1｝，得出的差集偶为：

D= ｛20，22，24，26，28｝= ｛1，4，3，12，9，10｝

D′= ｛21，23，25，27，29｝= ｛2，8，6，11，5，7｝

用差值证明如表1所示。

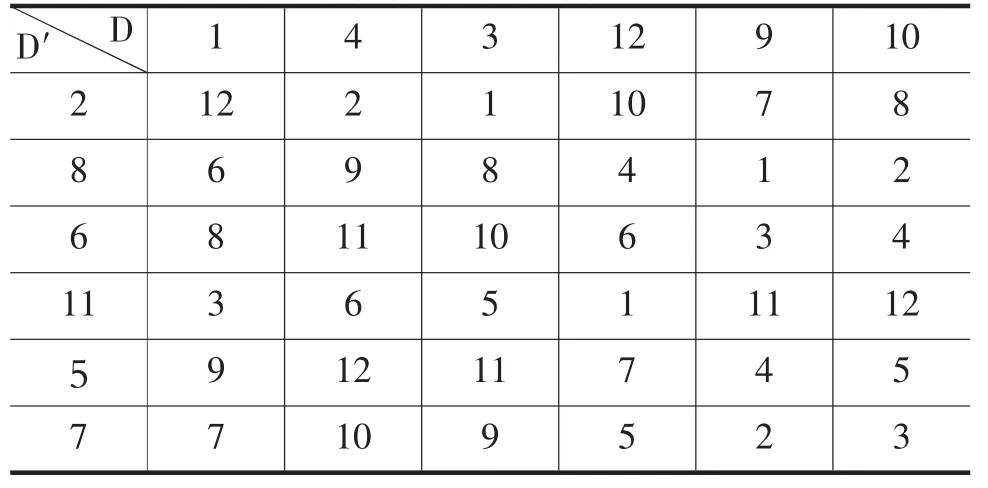
表1 奇素数13的两个分圆类的差

f为偶数的奇素数利用分圆类构造的差集偶的实例就列举这一个，其余都一样，只要符合定理1的条件就可以找出其存在的差集偶。

证明 若D与D′为（v，k，k′，e，λ），则（v，k，k′，e，λ）＝（q，f+1，f，0，（f+1）/d）对于任意元素g∈，方程x-y＝g，都恰有λ个解。设时，方程（1）的解除（1，1）个满足条件的解以外还有一个解（x，y）＝ （0，-g），因此1+（1，1）＝λ，因为此时，当i＝0时，方程满足条件的解的个数为（0，1）＝λ据引理［6］得：（1，1）+（0，1）＝f而（1，1）+ （0，1）＝2λ-1为奇数，所以f为奇数。

再证充分性：设f为奇数，且1+（1，1）2＝（0，1）＝f+1/2成立，对于任意元素，方程x-y＝g，的解的个数都是相等的，因此D确实是满足差集偶定义的一个差集偶，而得（v，k，k′，e，λ）＝（q，f+1，f，0，（f+1）/d）。

100以内是奇素数并且f为奇数的有3，7，11，19，23，31，47，59，67，71，79，83。根据新提出的分圆类构造差集偶的方法，找出q为这些奇素数时Fq加法群中的差集偶，并用差集偶的定义来直接证明这差集偶的正确性。

D=｛21，23，25，27，29｝U｛0｝=｛2，8，10，7，6，0｝

D′=｛20，22，24，26，28｝=｛1，4，5，9，3｝

最后集合中的元素是对11求余后的值。

用差值证明如表2所示。

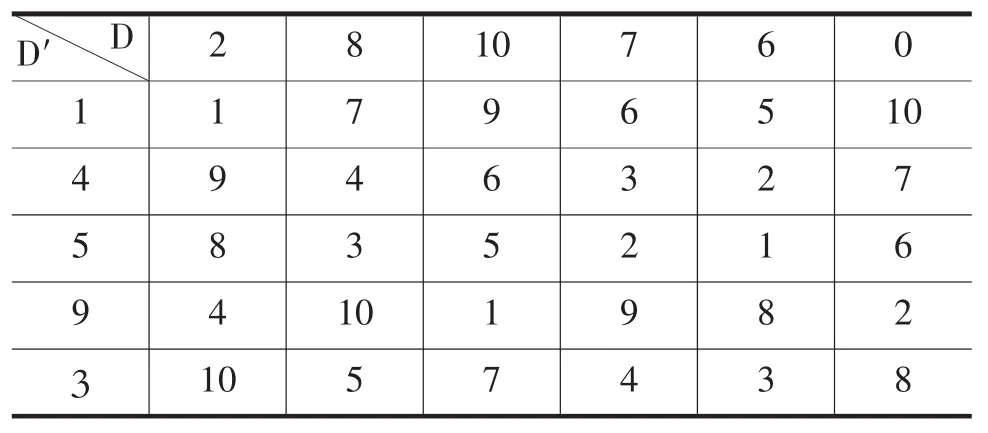
表2 奇素数11的两个分圆类的差

f为奇数的分圆类构造差集偶的例子就不再一一给出，只要满足定理2的条件都可以用分圆类构造出差集偶。

3 差集偶在最佳离散信号的应用

在通信系统中可用序列偶的优良的自相关特性提取有用信息。同时，若在码分多址通信中使用序列偶作为地址码，可提供两个地址码供两个用户使用。在信号处理中由于序列偶循环移位的方阵是正交的，所以可以用于信号交换，同时也可以用于信号实时处理［6］。而根据分圆类构造差集偶的方法得到的差集偶，对应能得到的是序列偶，最终把差集偶的研究应用到最佳离散信号设计中。

例3。根据定理1得到参数为（13，6，6，0，3）的差集偶。根据差集偶和序列偶的关系可以构造出存在的最佳二元序列偶。

D=｛1，4，3，12，9，10｝，D′=｛2，8，6，11，5，7｝构造出的最佳二元序列偶为：

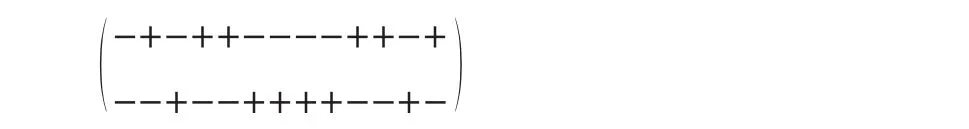
例4.根据定理2可构造出的差集偶—，根据差集偶和序列偶的关系可以构造出存在的最佳二元序列偶。

D=｛2，8，10，7，6，0｝

D′=｛1，4，5，9，3｝

构造出的最佳二元序列偶为：

4 结束语

本文主要基于分圆类和差集偶概念和性质，利用分圆类得到的差集偶构造出对应的最佳而二进序列偶；并把其应用到最佳离散信号设计中。众所周知，差集偶及其推广形式差集偶族是刚提出不久的新概念，有关它们的性质和构造方法等很多深层次问题需要进一步研究。这样，不仅能开辟一个数学研究领域，同时又将为新扩频通信地址码设计提供数学方法，进而推进扩频通信地址码设计的研究，使扩频通信系统的设计有更广泛的地址码选择范围。

［1］Thomas Storer.Cyclotomy and difference sets［M］.Markham publish company.Chicago，1967.

［2］许成谦.差集偶与最佳二进阵列偶的组合研究方法［J］.电子学报，2001，29（1）：86-89.

［3］贾彦国.几类最佳信号的研究［D］.秦皇岛：燕山大学，2003.

［4］刘红梅，姜晓云，刘桂枝.二进制频移键控的软件实现［J］.山西大同大学学报：自然科学版，2010，26（4）：23-25.

［5］张楠，王丽霞.基于DSP的载波通信模块设计［J］.山西大同大学学报：自然科学版，2009，25（4）：29-32.

［6］沈灏.组合设计理论［M］.上海：上海交通大学出版社，1996.

〔编辑 李海〕

Apply Cyclotomic Class to Signal Design

SUN Cai-feng1，LIU Hong-mei1，XING Jing-wei2
（1.School of Physics and Electronics Science，Shanxi Datong University，Datong Shanxi，037009；2.Liren College，Yanshan University，Qinhuangdao Hebei，066004）

This paper studies the constructions of the difference set pairs.Firstly，states the basic definitions and some properties of the difference set pairs and cyclotomic class，constructs some families of difference set pairs by means of single cycloomic class，and meantime，takes some examples to surrport the clam；Secondly，it uses difference set pairs that is constructed cyclotomic class to construct perfect binary sequence pairs；Finally，meanwhile，applyies cyclotomic class to study perfect signals design based on pairs by using the modern mathematical theory was made as well.

difference set pairs；cyclotomic class；sequence pairs；signal design

TN911.2

A

1674-0874（2011）01-0030-03

2010-10-15

孙彩锋（1981-），女，山西临县人，硕士，助教，研究方向：最佳离散信号设计。