因变量缺失的变系数部分线性模型的有效估计

李华鹏，蔡 凯

（山西大同大学数学与计算机科学学院，山西大同 037009）

因变量缺失的变系数部分线性模型的有效估计

李华鹏，蔡 凯

（山西大同大学数学与计算机科学学院，山西大同 037009）

讨论了因变量随机缺失条件下变系数部分线性模型的估计问题。基于局部借补思想，使用局部线性方法和平均技巧同时得到了各个估计量的估计，进而给出了估计的渐近性质。

变系数部分线性模型；随机缺失；借补

统计中经常碰到数据缺失的问题。处理缺失数据常用的方法有：基于完整数据的方法，加权方法及借补方法。人们也做了大量的工作。如Wang Qihua，Sun Zhihua［1］研究了当响应变量随机缺失时部分线性模型的估计，用核方法回归借补和边缘概率逆加权方法相应给出了协变量和非参函数的估计，并用经验似然推断方法给出了响应变量均值函数的估计；Chen Fan［2］研究了在响应变量为随机缺失条件下广义线性模型的局部拟似然估计，分别用局部拟似然方法，局部拟似然加权方法，局部拟似然借补方法给出了响应变量的估计，进一步给出了随机缺失条件下的响应变量的均值函数的估计；李志强、薛留根［3］在协变量随机缺失条件下，研究了广义半参数模型的加权拟似然估计方法，给出了未知参数与非参数回归函数的估计，并证明了所给出的加权拟似然估计的渐近正态性。三种常用的方法中，前两种都没有完全使用数据，造成信息缺失，且当有较多缺失值时，估计的真实效果会大打折扣，这时仅靠增大窗宽也是不行的，这样又产生了额外的偏差。对变系数部分线性模型［5-7］，文中讨论了当响应变量随机缺失［8］时，在张日权［6］的工作基础上，使用回归借补估计方法（能克服以上缺点）给出估计量的有效估计，并得到了其渐进性质。

1 估计和性质

考虑变系数部分线性模型其中Y为因变量，X∈R，U∈R，Z＝（Zj，…，Zp）T∈Rp是协变量，常数项函数α0（·）和变系数函数αj（·）为R上的未知可测函数（j＝1，…，p），随机误差ε满足

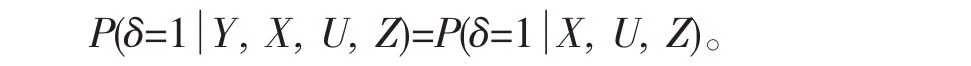
处理缺失数据，一种有效方法就是借补。张日权［6］用最小二乘法和平均方法同时求出了完整数据下α0（·），αj（·）的估计：

j＝0，1，…，p。这里ej是一个第j+1个分量为1的（2p+2）维单位向量，V为n×（2p+2）矩阵，第i行

g1，g2为初始窗宽。

文中借鉴此法，在此基础上令

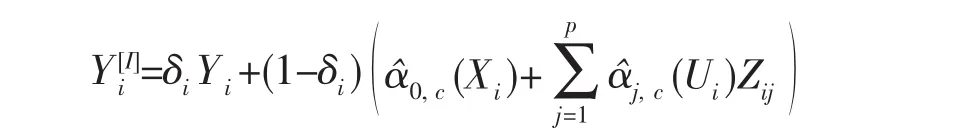
则当δi＝1时，＝Yi；当δi＝0时，

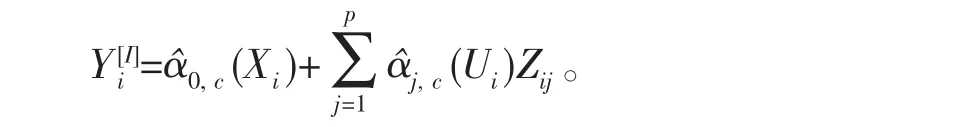
引入记号：令

T＝（X，U，Z），V＝（X，U），

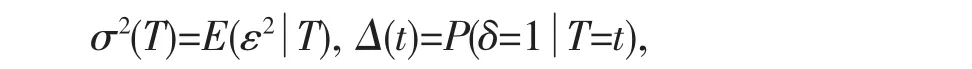
（A1）假设X和U的联合密度p（x，u），X的边缘密度p1（x），U的边缘密度p2（u）以及△（t）都是有二阶连续偏导数且是正有界的。

（A2，Gi，gi（·）是二阶可导的有有界支撑的核函数，i＝1，2。

（A3），都有连续一阶导数且是正有界的。其中A*B是矩阵A和B的Hadamard积。令

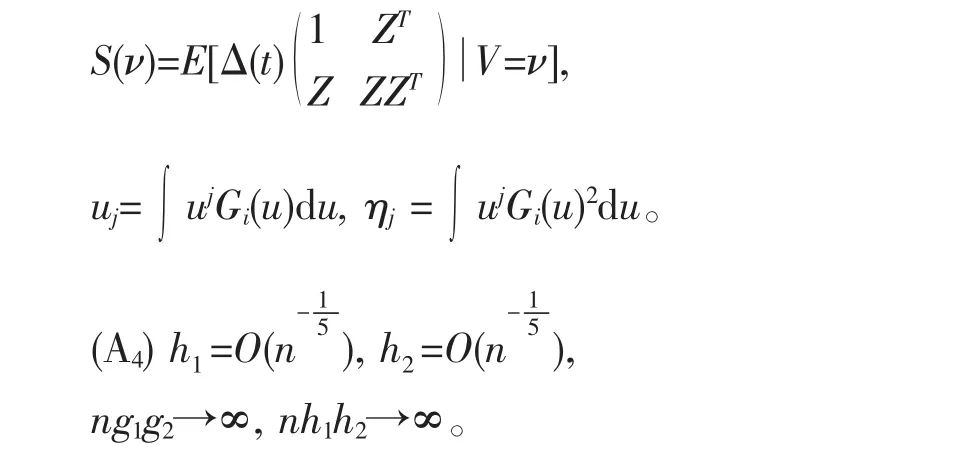
引理 由假设条件及g2/g1→0，有

证明 由文献［6］中定理2.1的结论和中心极限定理可得。

定理1 设上述假设条件成立，当h2/h1→0时，有

定理2 设上述假设条件成立及当g1/g2→0，g2/h1→0，h1/h2→0时，有

2 证明

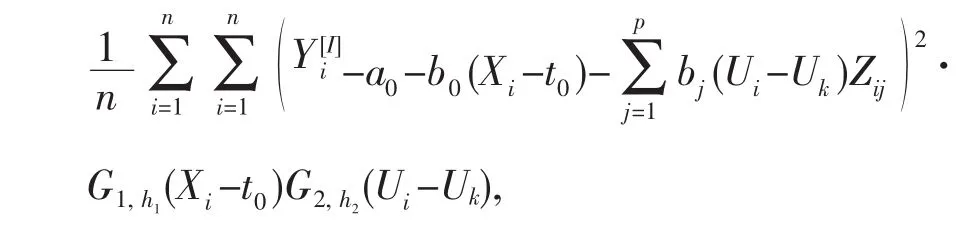
可得到

计算可得

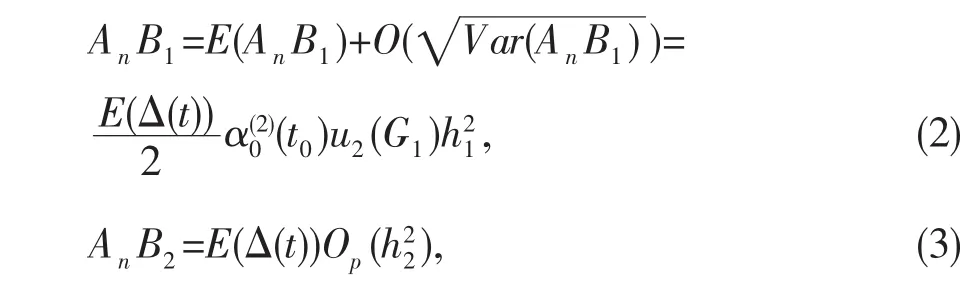
Anε服从正态分布，且

由引理可算得

综合（2）-（5）可知

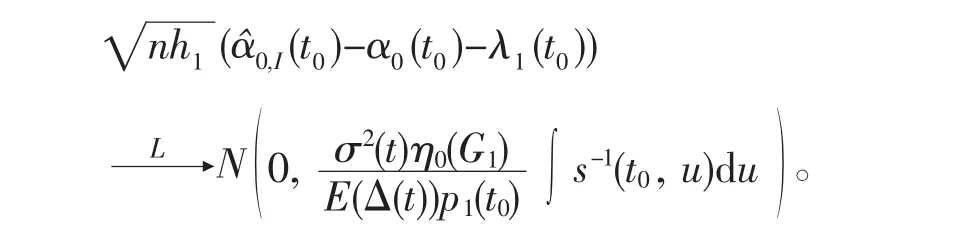
定理2的证明完全类似定理1的讨论可得。

［1］Wang Q H，Sun Z H.Estimation in partially linear models with missing responses at random［J］.Journal of Multivariate Analysis.2007（98）：1470-1493.

［2］Chen J W，Fan J Q，Li K H，et al.Local quasi-likelihood estimation with data missing at random［J］.Statica.Sinica.2006（16）：1071-1100.

［3］李志强，薛留根.协变量随机缺失的广义半参数模型［J］.北京工业大学学报，2007，33（7）：761-765.

［4］Zhang R Q，Lu Y Q，Zhang T S.Functional-coefficient Partially Linear Time Series Models for Hydrological Forecasting［J］.Advances and Application in Statistics，2006，6（1）：57-69.

［5］张日权，卢一强.变系数模型［M］.北京：科学出版社，2004.

［6］张日权.变系数部分线性模型的研究与分析［R］.北京：中国科学院数学与系统科学研究所，2003.

［7］冯井艳，张志强，李华鹏.变系数模型误差方差的估计［J］.山西大同大学学报：自然科学版，2010，26（1）：5-7.

［8］Roderick J A Little，Donald B Rubin.缺失数据统计分析［M］.孙山泽译.北京：中国统计出版社，2004.

〔编辑 高海〕

Estimation in Functional-coefficient Partially Linear Regression Model with Data Missing at Random

LI Hua-peng，CAI Kai
（School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

A functional-coefficient partially linear regression model is considered when the responses are missing at random（MAR）.Based on the method of the estimation with the imputed values，the local linear method and averaged technique are employed to give the estimators of all functions.Furthermore，the asymptotical normalities of all estimators are given.

functional-coefficient partially linear model；missing at random；local imputation

O211.7

A

1674-0874（2011）01-0007-02

2010-10-25

山西大同大学科学基金资助项目［2010K4］

李华鹏（1981-），男，河南周口人，硕士，助教，研究方向：数理统计。