特殊情形下线性模型异方差性的LM检验

郭彩霞

（山西大同大学数学与计算机科学学院，山西大同 037009）

特殊情形下线性模型异方差性的LM检验

郭彩霞

（山西大同大学数学与计算机科学学院，山西大同 037009）

考虑了特殊情形下具有异方差性的线性模型。首先导出了在模型中当异方差为线性函数时异方差检验的LM检验统计量及其性质，然后举例说明其有效性。

回归分析；异方差性；LM检验

通常的回归模型［1-3］都假设随机误差变量是独立同分布的。对参数进行假设检验通常的方法有：Wald方法，似然比方法，拉格朗日乘子法［4-10］。本文提出了当异方差为线性函数时异方差性检验的LM检验统计量，检验法，即拉格朗日乘子法。它的应用面很广。最后举例说明该方法的功效。

1 LM检验法

考虑如下线性回归模型：

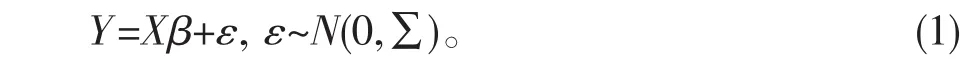
响应变量Y＝（y1，…，yn）T协变量Xi＝（1，Xi1，…，Xip-1）T待估参数β＝（β0，β1，…，βp-1）T随机误差ε＝（ε1，…，εn）T协方差阵Σ的主对角元素（i＝1，…，n）都大于零且不全相等，其余元素全为零。称模型（1）具有异方差性。

模型（1）是否具有异方差性即为如下统计假设检验：

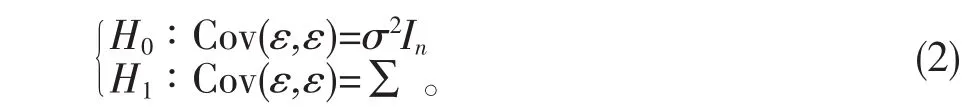
σ2为误差独立同分布时的方差。假定具有如下形式：

其中σ（·）是一个可微函数，σ（α0）＞0且σ′（α0）＞0，α0和α＝（α1，…，αq）T为待估参数，Zi＝（zi1，…，ziq）T，q＝1，…p-1为影响方差εi变化的因素。

此时对于模型（1），假设检验（2）又可表述为：

LM检验法是将零假设条件看成一个约束条件，通过对有约束的极大似然函数的一阶偏导数进行检验，对参数假设作出判断，记θ＝（α0，α1，…，αq）T，＝（θT，νT）T，ν＝（β0，β1，…，βp-1）T，

考虑假设检验问题

H0∶hj（）＝0，j＝1，…，k，k＜p。

由（1）式可知，在备择假设H1下，Y关于参数的对数似然函数

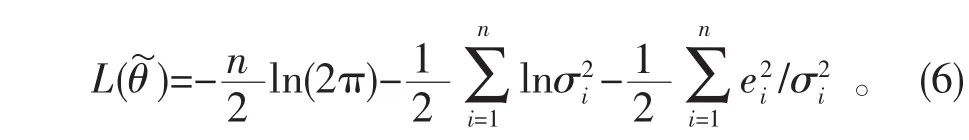
定理1 记参数ν＝（β0，β1，…，βp-1）′的极大似然估计为

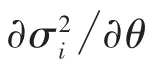
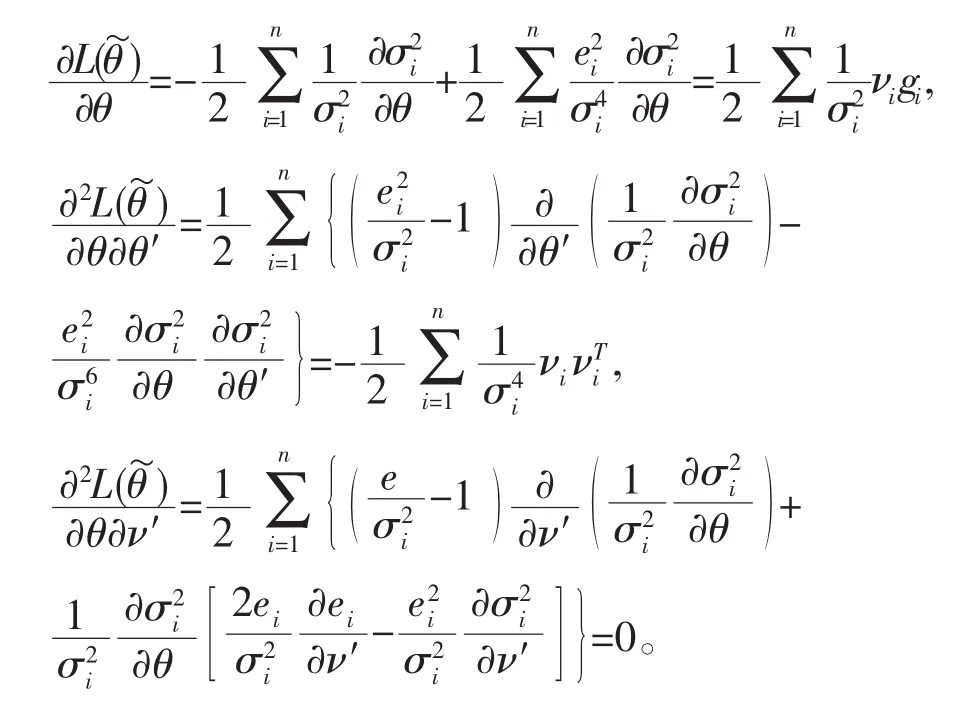
若零假设H0成立，则的有约束极大似然估计H0近似于的无约束极大似然估计。令

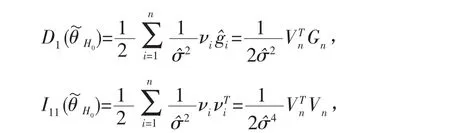
即可得所求的LM检验统计量

根据王松桂［6］可以证明，当H0成立时，

2 应用举例

模型：yi＝β0+β1xi+ei，ei～N（0，）。其中xi由如下方式生成：xi＝εi；ln（εi）～N（3，1），i＝1，…，n.。具有形式：＝σ2xi，i＝1，…，n。选择样本容量n＝20，30，40，50，60，70，80，每种不同的样本容量选择模拟重复1000次，由于异方差结构中仅含有一个未知参数，故由（7）可知，LM检验统计量的渐进分布为分布。对显著性水平10％，每次模拟计算相应的LM检验统计量的值，并与给定的显著性水平下的临界值相比，若该值大于临界值，则拒绝零假设H0，记录下1000次模拟中拒绝H0的次数的百分比。结果如表1：

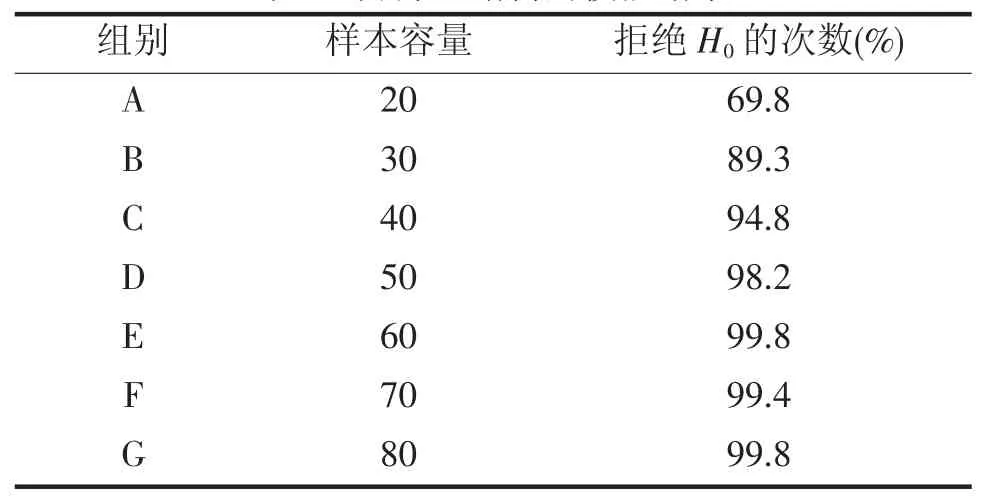
表1 异方差结构的模拟结果

结果表明，当样本容量n≥40时，H0被拒绝的百分比大于或接近0.9。

故LM检验对n≥40是有效的。

［1］冯井艳，张志强，李华鹏.变系数模型误差方差的估计［J］.山西大同大学学报：自然科学版，2010，26（1）：5-7.

［2］刘峰.部分线性模型的序列相关检验与异方差检验［D］.长沙：中南大学，2006.

［3］张霞峰.单指标模型的异方差检验［D］.上海：华东师范大学，2006.

［4］尹光霞.多元线性回归模型中的异方差性问题［J］.湖北大学学报，2003，25（2）：121-125.

［5］茆诗松，王静龙，濮晓龙.高等数理统计［M］.北京：高等教育出版社，2006.

［6］王松桂，陈敏.线性统计模型［M］.北京：高等教育出版社，2004.

［7］童恒庆.理论计量经济学［M］.北京：科学出版社，2005.

［8］陈希孺.数理统计引论［M］.北京：科学出版社，2007.

［9］吴喜之，王兆军.非参数统计方法［M］.北京：高等教育出版社，1999.

［10］范剑青，姚琦伟.非线性时间序列建模及应用［M］.北京：高等教育出版社，2005.

〔编辑 高海〕

LM Tests for Heteroscedasticity of Some Linear Models

GUO Cai-xia
（School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

A general heteroscedastic regression model is considered in a special setting.In this model，the heteroscedastic function is a linear function.A LM test for heteroscedasticity is established at first.An example is presented to show the efficiency of the method.

regression analysis；heteroscedasticlty；LM tests

O212

A

1674-0874（2011）01-0005-02

2010-09-11

郭彩霞（1980-），女，山西左云人，硕士，助教，研究方向：泛函分析。