例谈课本例题教学目标的落实

443400 湖北省五峰土家族自治县教研培训中心 雷 斌

例题教学是中学数学教师的教学任务之一，如何紧扣课标，结合教材内容要求，最大限度地挖掘和发挥例题的教学功能，落实它承载的教学目标，是值得每位数学教师深入研究的问题.本文从一个书本例题来谈例题教学目标的落实.

1 课本例题的教学设计

本例题出自于北师大版义务教育课程标准实验教科书八年级下册第147页.

图1

问题1如图1，AD是△ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，四边形PQRS是正方形.

(1)△ASR与△ABC相似吗?为什么?

(2)求正方形PQRS的边长.

分析本例题是学习“相似三角形对应高的比、对应角平分线的比和对应中线的比都等于相似比”之后的运用.从本节课的内容来看，它有三个要完成的知识技能目标为：一是复习三角形相似的判定;二是相似三角形对应高的比等于相似比的运用;三是运用方程思想解决几何问题.过程性目标：一是通过本例题的学习，学会未知的边用一个变量来表示的方法;二是通过变式练习，学会将未知的图形转化成已知的图形的方法，作出相应的高.

根据以上对本例题功能的分析，通过下面的教学设计落实教学目标.

活动1学生读题，完成问题(1)之后，教师提出问题：由△ASR与△ABC相似可得出哪些对应成比例的线段?设正方形的边长为xcm，那么AE的长度如何表示?

教学设计分析完成△ASR与△ABC相似的证明，落实知识技能目标一，学生不会感到困难，教师提出问题引导学生进一步思考解决问题(2)要找的等量关系，学生初步学会将未知的边用一个变量来表示的方法，落实过程性目标一.

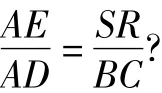
教学设计分析解答了问题(2)之后，学生对教师提出的问题进行思考，此处教师提出问题可以促使学生反思自己的学习行为，要解决问题，找到的等量关系必须只含有一个未知变量，如果还含有未知的其它量，要用已设的未知变量来表示，学会用方程思想解决几何问题，落实知识技能目标三，同时为问题2作铺垫.

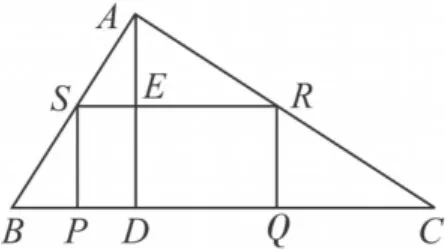
图2

问题2如图2，AD是△ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，四边形PQRS是矩形，且面积为S.

(1)如果设SP的边长为xcm，那么SR的长度如何表示?

(2)用含有x的代数式表示S.

教学设计分析本题将上题中正方形PQRS变成了长方形，在学习解一元二次方程之后，已知长方形面积，是可以求出长方形的边长的，在北师大版九(上)59页就有与之相似的题.

在此将问题和情境变化，作一个变式练习，用变量x来表示边SR，同问题1中求正方形边长是同一种方法，在此近一步强化用一个变量来表示其它变量的方法，找出相等的关系，进一步落实过程方法目标.

问题3如图3，在△ABC中，AB=AC=10cm，BC=12cm，点P，Q在BC边上，点R在AC边上，点S在AB边上，四边形PQRS是矩形，且面积为S，如果设SP的边长为xcm，用含有x的代数式表示S.

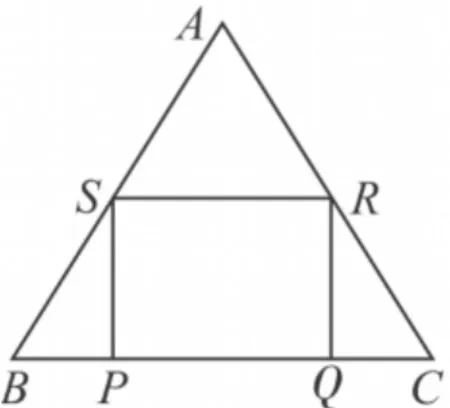
图3

教学设计分析本题将上题中的△ABC变成等腰三角形，同时BC边上的高不是已知条件，要用含有x的代数式表示S，必须作出BC边上的高，然后求出BC边上的高.设计此题，让学生掌握将变化的图形，转化成已学过的图形，同时学会这种作辅助线的方法，落实过程目标二，体会转化思想，从而学会这一类题的解法.为学习北师大版九(下))63页、69页相类似的题作好铺垫.

2 课本例题设计的教学启示

2.1 准确定位课本例题的教学目标

根据课程标准和教材内容，准确定位课本例题所要落实的教学目标.

从学生实际出发，补充和拓展例题内容.

2.2 教学中让学生经历“模仿练习、变式练习、反思感悟、获得方法”的过程

因为学生对解题方法的理解，有一个从被动到主动、从自发到自觉、从感性到理性、从模仿到创新、从内隐到外显的发展过程.如果教学中能有效地促使学生理解的深化，学生解决问题的能力就会提高，例题教学目标落实才真正到位.

2.3 通过有效提问，促使学生领悟解题思想、解题方法、问题的深层结构

学生在做题时，有时可以模仿，但为什么这样做，学生很少主动去思考，教学中通过教师的提问促使学生去思考.在完成问题2之后，教师要引导学生思考：求SR的长度与求正方形的边长方法比较;在完成问题3之前，教师引导学生思考：问题3与问题2的已知条件哪些变化了，哪些没有变化?促使学生去类比，从而获得解决问题的方法.