例谈试题模型建构的演变性

224054 江苏省盐城市亭湖区永丰初中 唐耀庭

例谈试题模型建构的演变性

224054 江苏省盐城市亭湖区永丰初中 唐耀庭

《全日制义务教育数学课程标准》强调：“让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程，进而使学生获得对数学理解的同时，在思维能力、情感态度与价值观等多方面得到进步和发展.”若将某些典型题图变异发展，形成一组能易中求活求深求精，融课本例习题、中考题于其中的提高型系列训练题组，则既能提高学生平时训练及综合复习的兴趣，使学生积极投入解题活动，又能以点带面，覆盖一片，同时还能从变换中创设习题教学新情境，引导学生探索演练，广开思路，拓展思维，培养思维灵活性和深刻性，提高解题能力，能使解某些数学题达到巧妙的境界，给人以赏心悦目的数学美的感受，本文以一道盐城中考试题进行模型建构的演变探究，供同仁参考.

原题 (2011年盐城)情境观察 将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A'C'D，如图1所示.将△A'C'D的顶点A'与点A重合，并绕点A按逆时针方向旋转，使点D，A(A')，B在同一条直线上，如图2所示.观察图2可知：与BC相等的线段是______，∠CAC'= ______°.

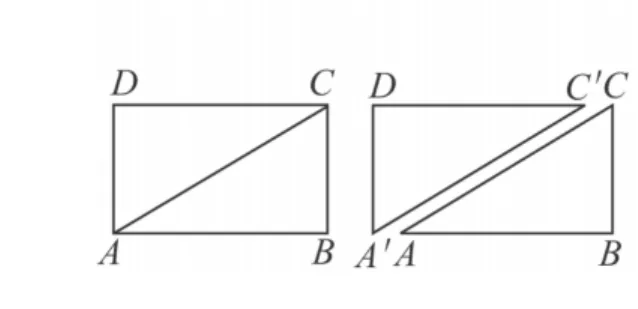
图1

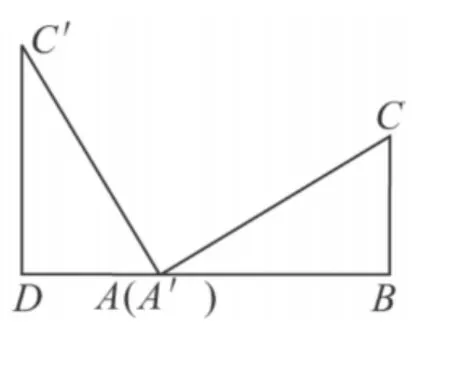
图2

问题探究 如图3，△ABC中，AG⊥BC于点 G，以 A为直角顶点，分别以AB，AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点 E，F作射线 GA的垂线，垂足分别为 P，Q.试探究EP与FQ之间的数量关系，并证明你的结论.

拓展延伸 如图4，△ABC中，AG⊥BC于点G，分别以AB，AC为一边向△ABC外作矩形ABME和矩形ACNF，射线 GA交 EF于点 H.若AB=kAE，AC=kAF，试探究 HE与HF之间的数量关系，并说明理由.

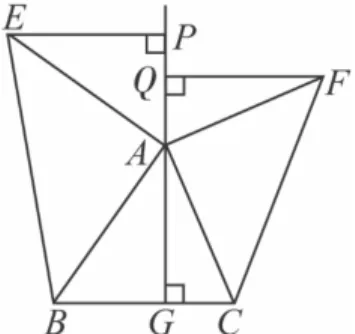
图3

1 试题赏析

1.1 正确的解题思路源于基础知识、基本技能和数学思想方法的熟练掌握

进入新课改后，各地纷纷出现了问题情境型新题型.该题型背景新颖、设问巧妙，能有效考查学生的自学能力以及观察分析、类比操作、抽象概括、数学归纳、语言表达等能力.本题的问题情境是通过操作积累，为学生提供了一个思维平台——以构造“三角形、矩形”为载体结合“拼图、旋转、全等、相似”等知识解决问题.并由此提供了解决问题的方法.

第(3)问只是在问题情境的基础上设置了一个台阶(将三角形变为矩形)，解此试题，必须把握住试题的核心，与问题探究相仿，只不过将全等改为相似，可以借助第(2)问构建的几何模型：证出FQ=AG.再证Rt△EPH∽Rt△FQH，从而使得问题解决.使得实际问题数学化，数学问题形象化，体现了不同数学知识之间的相似性.本题考查的思想方法有：建模思想、转化思想、数形结合思想.

1.2 试题高超的设计技巧和良好的思维策略

本题设问层层铺垫，思维层次逐步递升.第(1)问是对新建数学模型的再认识，第(2)问是对新建模型的灵活应用.这两问帮助学生同化新建数学模型，为下一问题的解决作铺垫.是思维层次上的一个跳跃，该问同时较好地考查了学生的思维策略：首先恰当地选用图形解决问题;其次要观察图形，对复杂图形要善于分解，弄清楚不同的构成要素(AB=kAE，AC=kAF);最后要大胆猜想，严谨论证，用相似知识解决问题(HE=HF)，启发我们在今后得教学中要注重几何模型的教学.

2 试题模型建构的演变探究

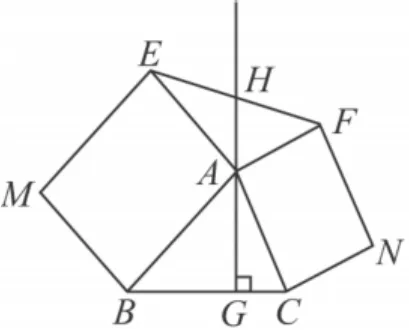
图4

新课程强调：数学模型的应用价值，一方面，是从实际问题中抽象出遇到的问题，回归到数学模型，通过解决数学问题，完成对数学问题的解答;另一方面，就是以数学的眼光，审视实际生活中数学模型的“原始状态”，学以致用.使问题具有一定的探究空间.有鉴于此，笔者对此题做了如下演变.

2.1 模型探究1 改变条件，探究结论

例1 如图5，图6，以△ABC的边AB，AC为直角边向外作等腰直角△ABE和△ACF，M是BC的中点，请你探究线段EF与AM之间的数量关系.

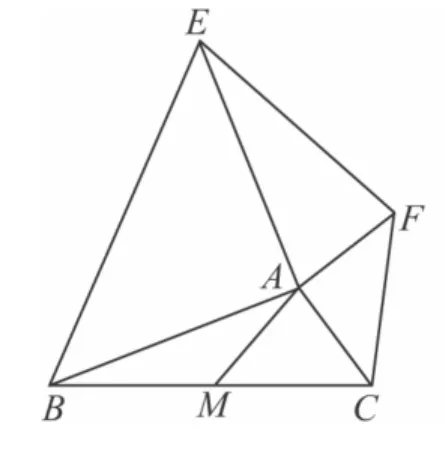
图5

图6

解析 利用中点的中心对称性，将△CAM绕点M顺时针旋转180°，构造平行四边形证明

(1)如图7，延长AM 至 N使MN=AM，(或将△CAM绕点 M顺时针旋转 180°得△BNM)连接 BN，CN则四边形ABNC是平行四边形，BN=AC，∠BAC+ ∠ABN=180°，

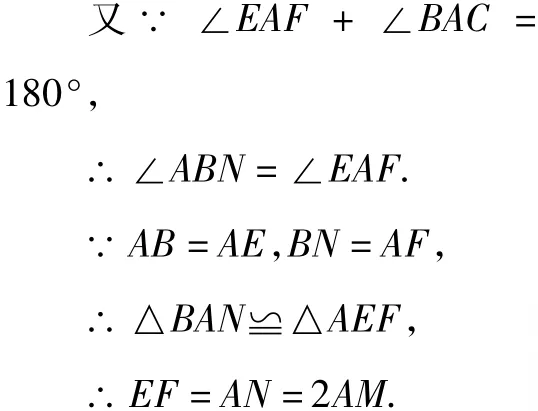
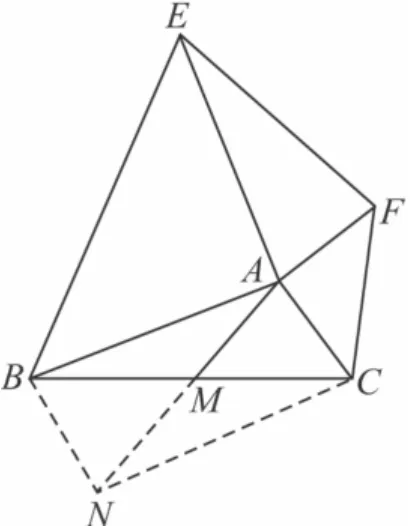
图7

(2)如图 8，延长 AM至N使MN=AM，连接 BN(或将△CAM绕点M顺时针旋转 180°得△BNM)则AC=BN，∠BAC+∠ABN=180°.

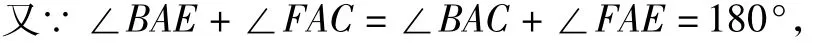
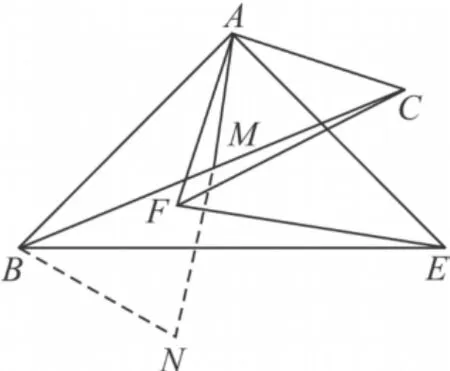
图8

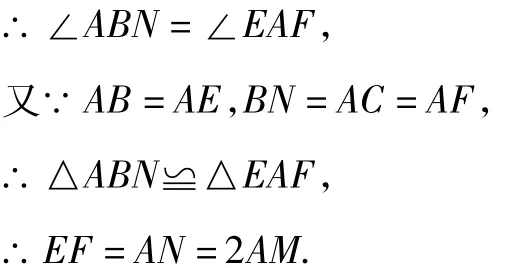
2.2 模型探究2 引申结论，步步深入

原题设不变，若连接BF，CE交于点P，则线段BF，CE有何位置关系?

解析 设BF，AE交于点Q.

如图9，BF=CE且 BF⊥CE，

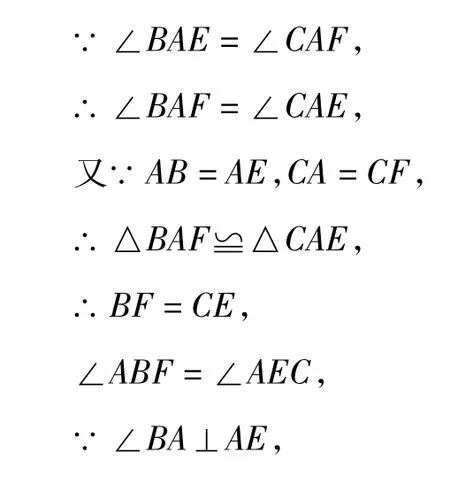
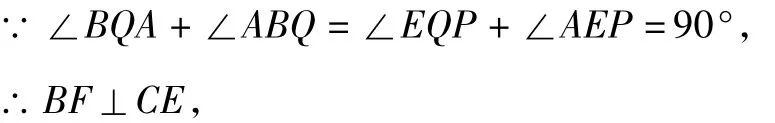
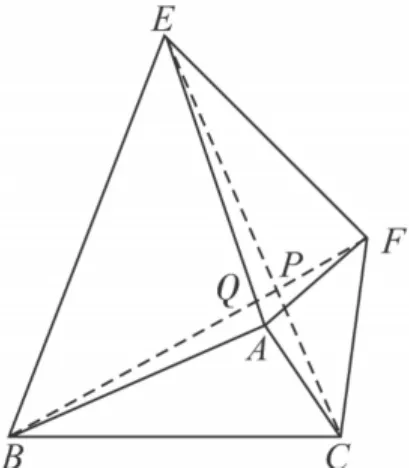
图9

如图10，BF=CE且BF⊥CE，

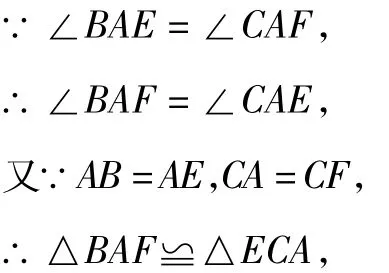
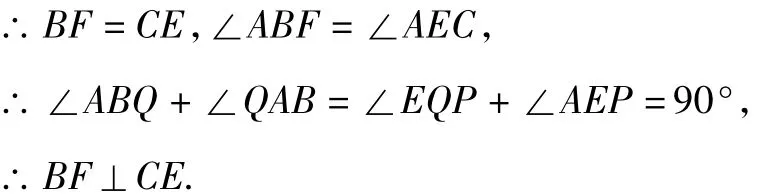
点评 将△ABE，△ACF绕A点任意旋转一个角度，都存在BF=CE且BF⊥CE这一结论.

2.3 模型探究3 巧改条件，另立新意

例2 变换中点位置将△ABE，△ACF绕A点任意旋转一个角度，取斜边BE，CF的中点M，N，线段MN，AP又有何关系?

解析 如图11.连接 MP，MA，NP，NA，

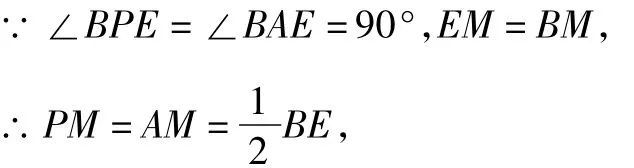
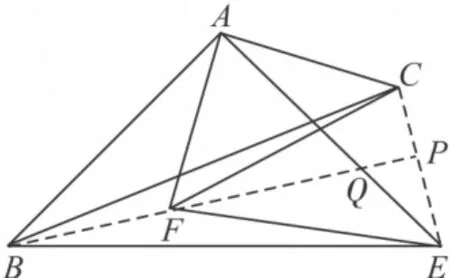
图10

∴点M在线段AP的垂直平分线上，同理点N在线段AP的垂直平分线上，

∴线段MN垂直平分线段AP.

如图12，连接 MP，MA，NP，NA，

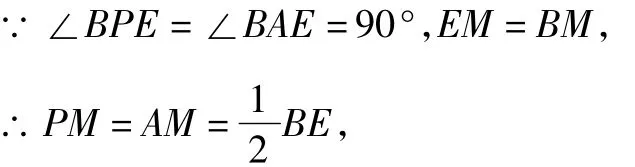
∴点M在线段AP的垂直平分线上，同理点N在线段AP的垂直平分线上，

∴线段MN垂直平分线段AP.

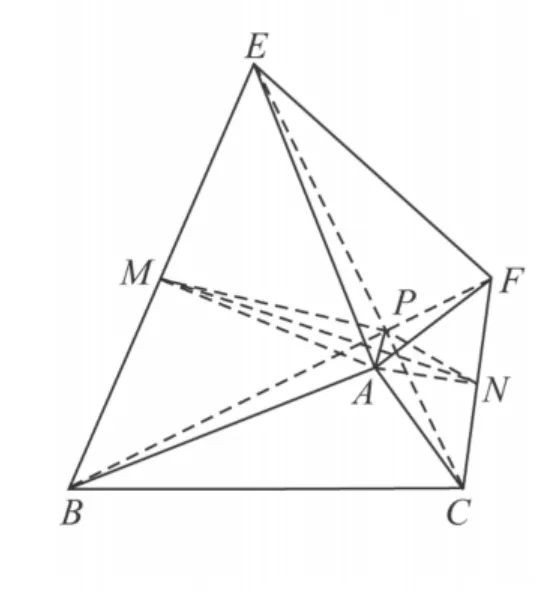
图11

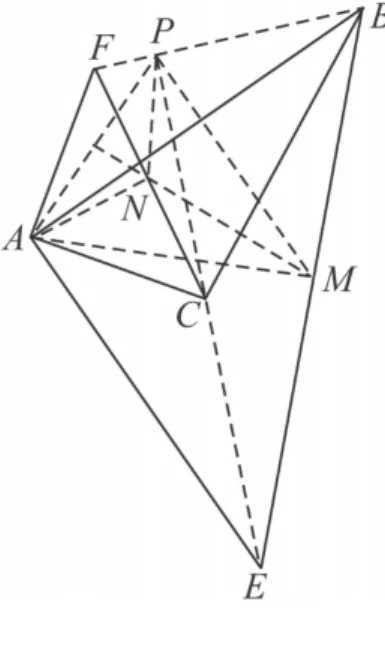
图12

2.4 模型探究4 强化条件，殊途同归

例3 在图9，图10的基础上，以AB，AC为边作正方形ABFE，正方形ACGF，M，N分别是两个正方形的中心，若正方形ABFE和正方形ACGF的面积分别为338及200，在旋转过程中使得AP=10，求MN的长.

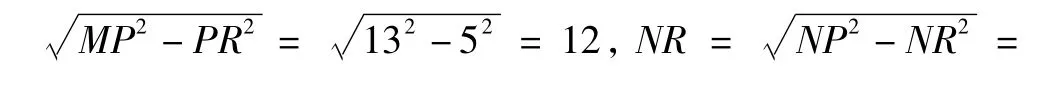
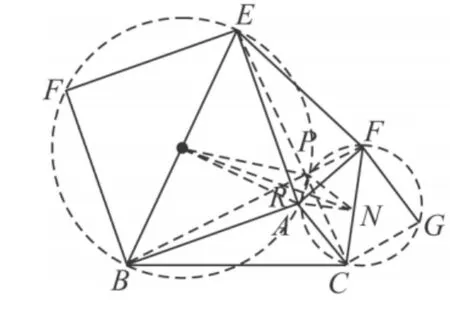
图13

图14

2.5 模型探究5 调换条件，使问题特殊化

(1)若⊙O'与⊙O外切于点 A(见图15)，EA，BA的延长线分别交⊙O'于点C，F，连接CF，则△ACF是_________三角形;

(2)若⊙O'与⊙O相交于点 A，P(见图 16)，连接EP，BP并延长分别交⊙O'于点C，F，请选择下列两个问题中的一个作答：

图15

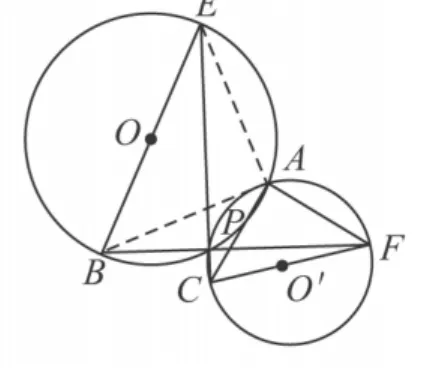
图16

问题1 判断△ACF的形状，并证明你的结论;

问题2 判断线段EC与BF的关系，并证明你的结论.我选择问题_____，结论：__________________.

(3)若⊙O'与⊙O内切于点A(见图17)，AE，AB分别交⊙O'于点 C，F，连接 CF，则△ACF 是_______三角形;

(4)若⊙O'与⊙O相交于点 A，P(见图 18)，连接EP，BP并延长分别交⊙O'于点C，F，请选择下列两个问题中的一个作答：

问题1 判断△ACF的形状，并证明你的结论;

问题2 判断线段EC与BF的关系，并证明你的结论.我选择问题_____，结论：_____________________.

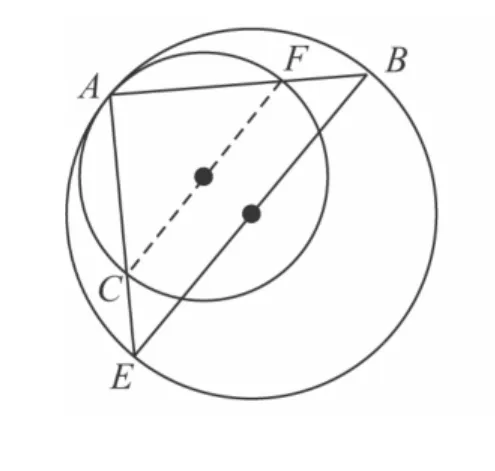
图17

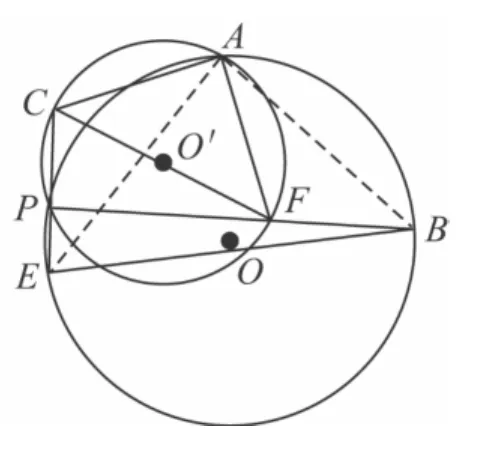
图18

解析 (1)等腰直角

(2)问题1 △ACF是等腰直角三角形

证明 连接AE，AB，

问题2 连接AE，AB，∴ ∠EPB=∠FPC=90°，

2.6 模型探究6 变换形式，迁移深化

将三角形变为正方形设计得如下两题

例5 如图19，正方形ABCD中，E，F 分别是 AD，AB 的中点，过点A作AM⊥BE，交对角线BD于M，连接ME.探究ME与DF之间的位置关系并证明.

解析 ME⊥DF 将△ABE沿BA方向平移BA的长度，再绕点A顺时针旋转90°(或延长AM交DC于点H)得∠DHA=∠AEB，DH=AE，

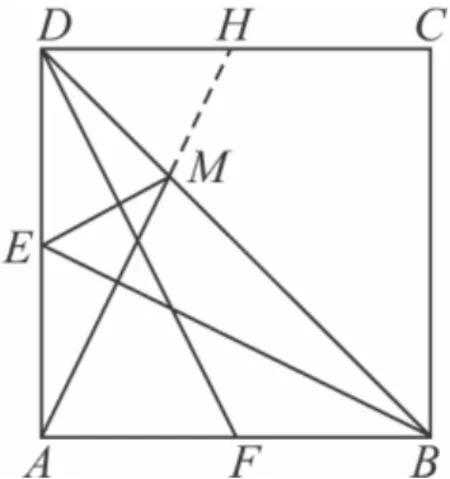
图19

例6 如图20，若E，F分别是 AD，AB 上的点，且 AE=AF.过点A作AM⊥BE，交对角线BD于M，过点M作 MG⊥DF，交 AD于N，交BE的延长线于G.探究BG，AM，MG之间的数量关系并证明.

解析 BG=AM+MG 将△ABE沿BA方向平移BA的长度，再绕点A顺时针旋转90°(或延长AM交DC于点H)，

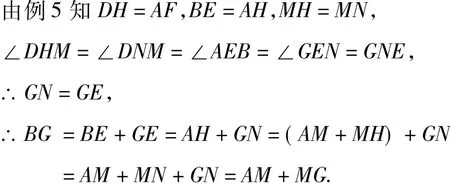
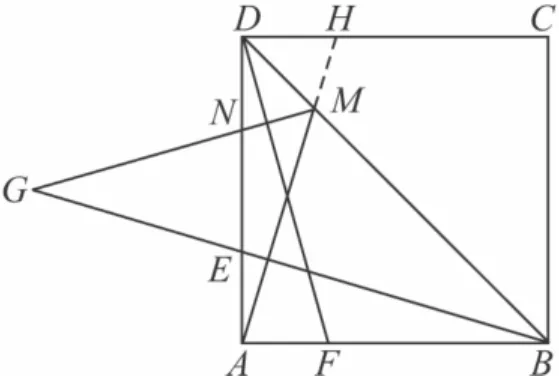
图20

20110823)