抓住基本图形教学 提升数学思维水平

430079 华中师范大学教育学院 刘 辉

抓住基本图形教学 提升数学思维水平

430079 华中师范大学教育学院 刘 辉

平面几何是初中数学一个重要的内容模块.初中数学的平面几何内容以欧几里德的《几何原本》所建立的公理化体系为基础，对于培养学生的逻辑推理能力、培养学生的理性思维、形成实事求是的态度有重要的作用.然而，现实情况下，一些学生感到几何难学，或是学习效果不佳，畏惧几何，继而畏惧数学，甚至放弃数学学习.“对初中生来说，首先是几何比代数难学，许多学生连“基本题”也做不好;其次是“两极分化”……［1］，那么，怎么样解决这些问题?

《全日制义务教育数学课程标准(实验稿)》在几何内容的学习方面，要求学生“能从较复杂的图形中分解出基本的图形，并能分析其中的基本元素及其关系”“利用直观来进行思考”［2］.“平面几何的教学，从某种意义上讲，就是教会学生认识基本图形的性质，引导学生运用基本图形的方法去分析和解决问题，培养学生的逻辑思维和逻辑推理能力”［3］.抓住基本图形的教学，有助于在学习过程中提升学生的思维水平.

1 基本图形及基本图形法的含义

1.1 基本图形

关于基本图形的含义，学界并没有一个统一的界定，它不像一些基本的数学概念那样严格清晰.只是在长期的教学实践过程中，人们对基本图形形成了一些相对稳固的约定与共同的认识.傅佑珊老师认为，“现行中学平面几何课本中概念、定理、公理所对应的图形都称为基本图形.”可以说，基本图形是内容和形式的统一体.因为，每一个几何概念、每一条几何公理、定理及定理的推论都对应着一定的图形.

基于此，平面几何中的基本图形有概念型基本图形与定理型基本图形(包括公理、定理的推论在内)之分.这两大类型的基本图形大致将教科书上平面几何知识点包括在内了.还有一类也可作为平面几何中的基本图形，称之为经验型基本图形.因为，以这一类基本图形为基本构图的几何题会以相关的形式稍有变化地在学生的练习题中出现，有了相关的经验型的基本图形，能够快速引领学生找到解题的方向.

具体说来，三种基本图形的含义如下.

1.1.1 概念型基本图形

即几何概念所对应的图形.直线、角、三角形、矩形、正方形、菱形，圆等.每一个几何概念对应着一定的图形.

1.1.2 定理型基本图形

这一类基本图形将公理、定理及推论对应的图形包含在内，它们区别于概念型基本图形之处的是，图形的元素(如线段、角)之间有一定的数量上或空间位置上的相互关系.平面几何中一般的定理分为性质定理与判定定理.一般是满足一定的条件，才会有一定的结论.如两直线平行，同位角相等(如图1);角平分线上的点到角两边的距离相等(如图2).一条定理、公理也对应着一定的图形.

1.1.3 经验型基本图形

此类基本图形是在教学过程中，或是学生的学习过程中遇到的，具有一定代表性的、典型的基本几何图形，是一个开放的系统，通常具有从经验中积累的特点.教师在几何教学过程中可以指导学生注意此类图形所包含的几何性质、结论的总结，如“母子相似三角形”(如图3)、“射影定理”(如图4)、“角平分线加平行线会有等腰三角形”(如图5)等.每个人都可以在自己的经验积累的基础上进行总结，这样的范例式图形越丰富，学生学起几何来也就越容易.一般综合性较大、学生感到困难的几何题，究其本质也就是一些基本图形的叠加与组合.

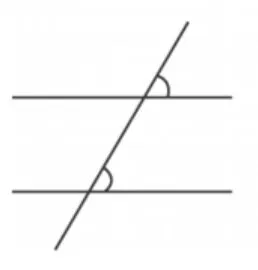
图1

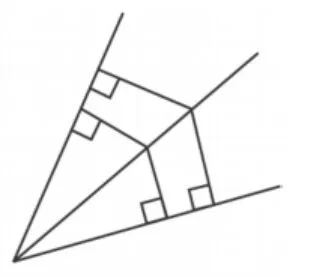
图2

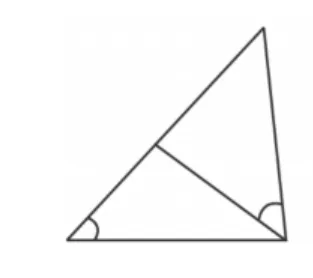
图3

图4

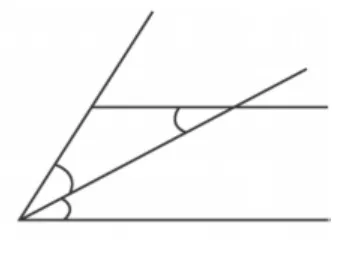
图5

1.2 基本图形法

基本图形法，是指“在几何图形中分解或构造出起主要作用的基本图形，通过这些基本图形建立已知条件与要得出结论之间的联系，以求得问题的解决.”

让学生学会运用基本图形法，对复杂的几何图形进行分解，从中抽出基本图形出来，对于提高学生的几何解题能力有着直接的促进作用.

2 基本图形教学的运用

所谓抓基本图形的教学，一是教师在几何内容的教学过程中要以平面几何中的基本图形为出发点，让学生以此为抓手，掌握基本的概念、定理、公理等基本知识，即知道有哪些知识可用;二是教学生会用基本图形法，在纷繁复杂的几何图形中分解出基本图形出来，化繁为简，化难为易，即掌握知识该怎样运用.

下面从知识表征、知识的掌握记忆、复杂图形的分解等方面来研究基本图形在教学中的运用.

2.1 运用基本图形掌握数学概念

以“三线八角”为例，如图6这一基本图形之中包含了同位角、内错角、同旁内角三个相关的概念.这三种角的共同特征都是由两条直线被第三条直线所截而成的角，而角与角之间不同的位置关系也就造成了三类角的名称的不同.有学生在学习这些概念时要么对于单独的一种角的判断错误，要么是对于这三类角的判断互相混淆.在教学过程中，一般是一个一个地解决，先让学生借助这幅图，结合教师对概念的讲解，依次理解同位角的含义、内错角的含义、同旁内角的含义.分别学习三类角的概念之后，为检验他们是否真正掌握理解了三类角概念的含义，让他们在一幅图中指出同位角有哪些、内错角有哪些、同旁内角有哪些.当学生能在一幅图中清楚准确地分辨出三类角时，就表明学生对这三类角的概念含义已完全掌握了.

图6

教科书上对几可概念是用语言文字形式进行表征的，相对而言，概念型基本图形对几何概念以图象形式进行的表征更为形象、直观.从认知心理学的角度来看，几何图形作为一种视觉通道的信息，更容易在人的头脑中形成表象，对于知识的表征以图象的形式贮存.这种表征适合处于初中阶段的学生的思维发展水平，使知识变得更易于理解和接受.相反，如果，不注重概念型基本图形，而只关注于对文字进行解释的角度来把握概念，那么，效果就会大打折扣.抓住概念型基本图形，有助于促进学生对几何概念的理解掌握，这为他们进一步学习几何知识打下基础.

2.2 运用基本图形成良好的知识结构

以人教版九年级下册的锐角三角函数这一章节知识为例.要想顺利地解决解直角三角形的问题，理解掌握30°，45°，60°这三个特殊锐角的正弦值、余弦值及正切徝是必须过的第一关.有学生在学习这一章节的内容时，总是记不住，记错或记混了.其实，只需要抓住两个特殊的直角三角形，即等腰直角三角形与一个角是30°的直角三角形，它们三边之比分别是1∶1∶，1∶∶2，再结合正弦、余弦、正切它们的定义，即对边比斜边、邻边比斜边、对边比邻边;就很容易地得出这三个特殊锐角的三角函数值了，在理解的基础上记忆这些三角函数值也就没什么困难了.

平面几何知识主要是以陈述性知识的形式进行呈现的.在对陈述性知识进行学习过程中，记忆是必须的.后继的学习将以前面掌握的知识为基础，因此必须要保持记住一些知识块.而从记忆的策略来讲，零散的知识点形成的知识结构太过于分散，不利于形成知识模块.运用基本图形，结合相关的概念定义，有助于理清知识点之间的来龙去脉及相互关系.即不仅是促进学生对于知识的理解，而且有助于促进学生对知识的保持记忆，形成良好的知识结构.

2.3 运用基本图形法，分析复杂的几何图形

在平行线的性质里有“两直线平行，同旁内角互补”这一条.对应的基本图形，如图7比较简单，属于定理型基本图形.在此基础上，稍有变化形成图8.这时四条线形成的三个角之和为360°，也不算难.

图7

图8

图9中，x轴与y轴交于O点，AB交 y轴于 A点，DE交 x轴于 E点，AB∥DE，∠OAB与∠OED的角平分线交于P点，求∠P的度数.

分析 此题借助基本图形图8的基础，从图中分解出B-A-O-E-D这个图，利用图8的结论，

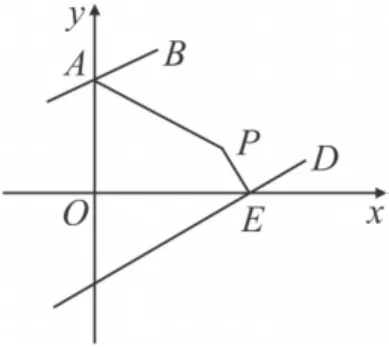
图9

四边形PAOE内角和为360°，

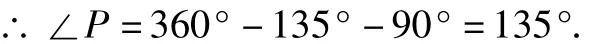
3 基本图形教学中蕴含的数学思想方法

基本图形法并不只是简单地为了解决微观层面的学生学习过程中的问题，这种方法蕴含了更高层面的数学思想方法.教师通过基本图形法在教学中的运用，有助于向学生渗透数学思想方法，从而提升学生的数学思维水平.

3.1 数形结合思想

“数缺形时少直观，形缺数时少精确”.这句话准确恰当地点明了数与形之间的重要联系.在学习数学过程中培养学生形成数形结合的思想，有助于他们“数学化”地思考问题，即从数学的角度来看问题，具体到平面几何知识上来说，更是少不了对图形的关注.平面几何本来就是以平面图形的性质特征为主要研究内容的.此外，在几何知识与代数知识相结合的地方，即既需要考查图形间的相互位置关系，同时也需要关注图形中的数量关系的时候，运用数形结合思想是很自然的了.如文中提到的锐角三角函数运用到解直角三角的相关问题时，就是一个典型的例子.

3.2 转化、化归的思想

数学知识体系是以一定的逻辑建立在基础知识之上的.因而对后续知识的学习必须要以前面基础知识的掌握为依托，否则，后续的学习无法进行.在遇到复杂问题时，我们总是尽量把它往已熟悉的内容上转化、化归.化未知为已知、化繁为简、化难为易.

基本图形法就是这样一种方法，面对纷繁复杂的几何图形，从众多的线条中分解、抽出基本图形，是一项重要的几何思维能力.分解、抽出基本图形出来，尤其是经验型基本图形，即将任务难度进行分解，将不熟悉的转化为已熟悉的，将复杂的任务化为简单的任务的过程.

3.3 综合法与分析法相结合的思想

这一思想是紧承转化、化归思想而来.运用基本图形法从复杂的图形线条中抽出基本图形以后，任务难度就降低了，这是一种分析的方法.即要解决这个问题，需要先满足什么条件;而要满足这个条件，又必须先满足什么条件，这样一步步往前追踪，追踪到某一个基本图形时，需要的条件满足了.再按原路返回，倒过来推理，结合其他条件，进行证明或解答的过程，就是综合法.基本图形法在解决平面几何的过程中，起到了连接分析法与综合法的桥梁的作用.如果没有基本图形法的思路来找到熟悉的基本图形，思维链可能就会断开，继而影响到问题的解决.而有了基本图形作纽带，再使综合法与分析法相结合，问题就能得到很好的表征，解决起来也就简单得多.运用基本图形法解决问题的过程中，包含了综合法与分析法相结合的过程.

1 张奠宙.平面几何教学的回顾与前瞻［J］.数学教学，2005，5

2 叶尧城，向鹤梅主编.全日制义务教育课程标准(修订稿)教师读本［M］.武汉：华中师范大学出版社，2003，6.

3 傅佑珊.浅谈平面几何图形的基本教学［J］.数学通报，1993，5

4 傅佑珊.平面几何基本图形的方法与教学实践［J］.北京教育学院学报，1997，2

20110822)