走进压轴题的“路径长”

210019 南京金陵中学河西分校 李玉荣

为了体现中考的选拔功能，中考命题者特别关注初高中数学知识的衔接，在衔接点处精心设置压轴题，已成为中考命题的一种时尚.近年压轴题出现的“求点运动的路径长”是高中解析几何“求点的运动轨迹方程”的雏形，它不同于几何课本中单纯代入公式求解的一些几何计算题，也不同于单纯考查逻辑思维的几何证明题，需要数形结合，边推理边运算，有很强的探索性，体现知识的发展过程，考查学习潜能，内涵丰富、立意新颖，使中考命题真正实现了由“知识立意”向“能力立意”的过渡，不仅有利于高一级学校选拔合格的新生，而且对初中数学教学具有良好的导向作用.

1 运动路径为线段

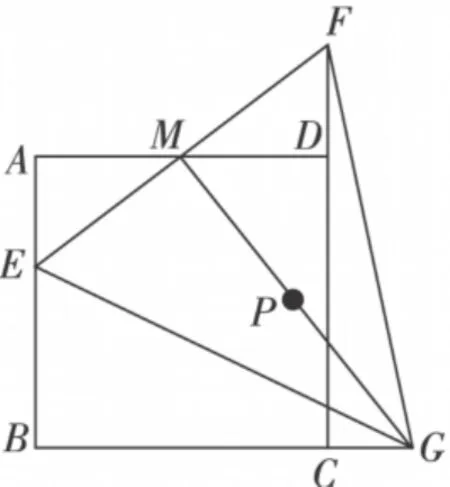
图1

例1(2010年南京)如图1，正方形ABCD的边长是2，M是AD的中点，点E从点A出发，沿AB运动到点B停止.连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG，FG.

(1)设AE=x时，△EGF的面积为y，求y关于x的函数关系式，并写出自变量x的取值范围;

(2)P是MG的中点，请直接写出点P运动路线的长.

简解(1)略;

(2)如图2，当点E与A重合时，

显然BG1=AM=1;

当点E与B重合时，

由△AMB∽△MBG2，

易求得BG2=5，

所以G1G2=4，

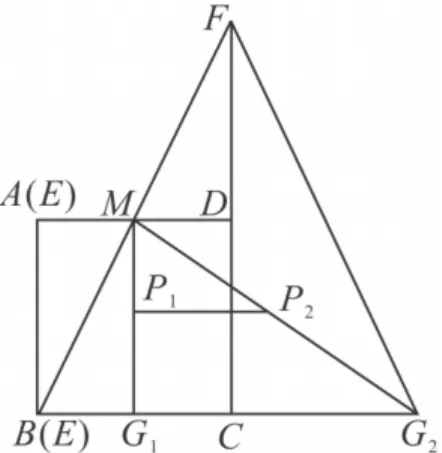
图2

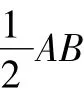
点评 第(2)题中P为动点，求点P运动路线的长，可考虑点E的极端位置——初始点A，终止点B，相应的点P的起始位置分别为P1，P2，再经探索得到点P运动路线为线段P1P2，从而可求出点P运动路线的长.

例2(2011年三明)在矩形ABCD中，点P在AD上，AB=2，AP=1.将直角尺的顶点放在P处，直角尺的两边分别交AB，BC于点E，F，连接EF(如图3).

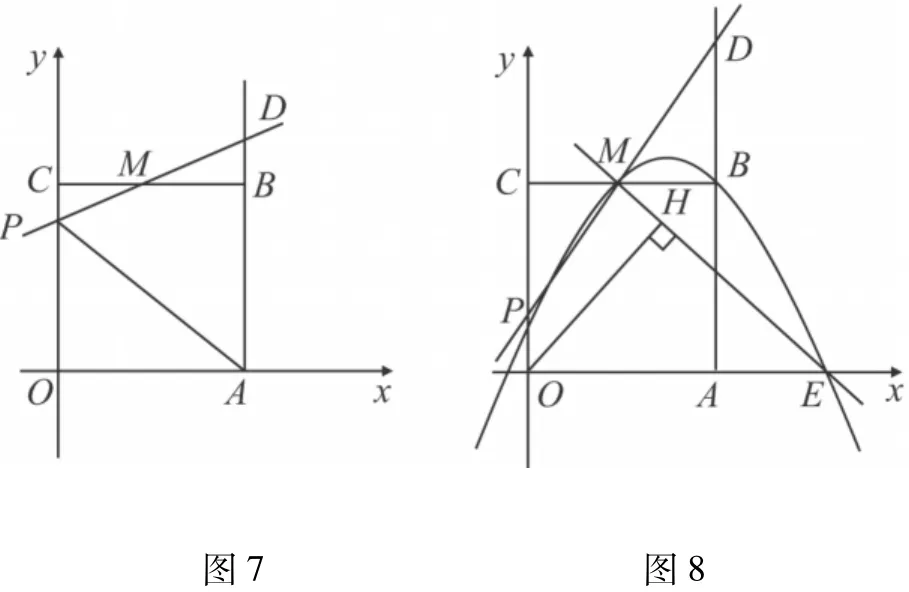
(1)当点E与点B重合时，点F恰好与点C重合(如图4)，求PC的长;

(2)探究：将直尺从图4中的位置开始，绕点P顺时针旋转，当点E和点A重合时停止.在这个过程中，请你观察、猜想，并解答：

①tan∠PEF的值是否发生变化?请说明理由;

②直接写出从开始到停止，线段EF的中点经过的路线长.

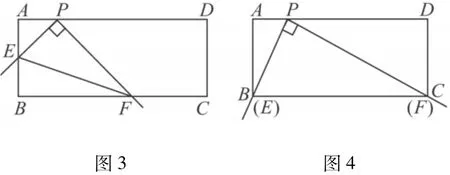
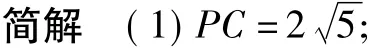
(2)①tan∠PEF的值不变;

点评第(2)②题中线段EF的中点为动点，求它运动路线的长，关键是抓住题设中直角尺旋转的开始位置与停止位置，确定线段EF的中点的起始位置，再经探索知线段EF的中点经过的路线为线段，从而可求出路线长.

2 运动路径为圆孤

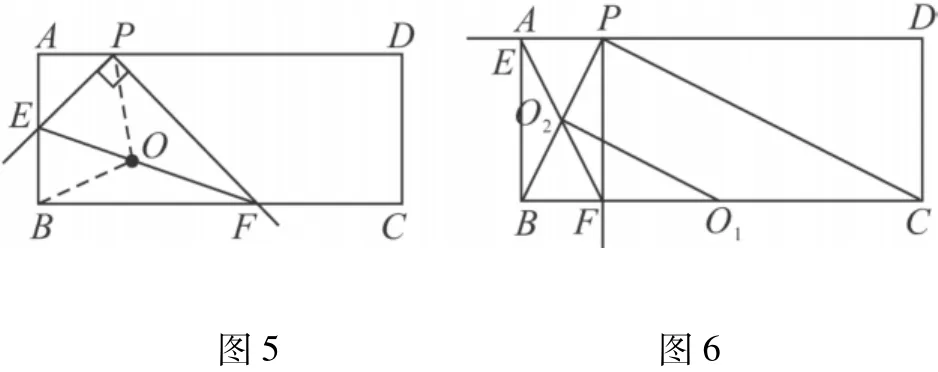
例3 (2011年湖州市)如图7，已知正方形OABC的边长为2，顶点A，C分别在x，y轴的正半轴上，M是BC的中点.P(0，m)是线段OC上一动点(C点除外)，直线PM交AB的延长线于点D.

(1)求点D的坐标(用含m的代数式表示);

(2)当△APD是等腰三角形时，求m的值;

(3)设过P，M，B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H(如图8)，当点P从点O向点C运动时，点H也随之运动.请直接写出点H所经过的路径长.(不必写解答过程)

简解(1)点D的坐标为(2，4－m);

(2)当△APD是等腰三角形时，

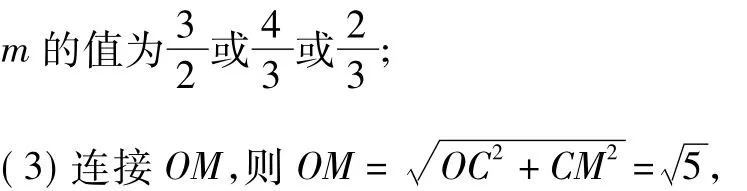
设OM的中点为O1，

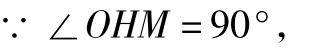
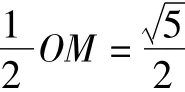
可考虑点P的极端位置：当点P从点O开始运动时，

过P，M，B三点的抛物线为y=－x2+3x，点E(3，0)，易知∠MEO=45°，

可得∠EOH=45°，所以∠COH=45°;

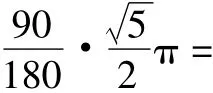
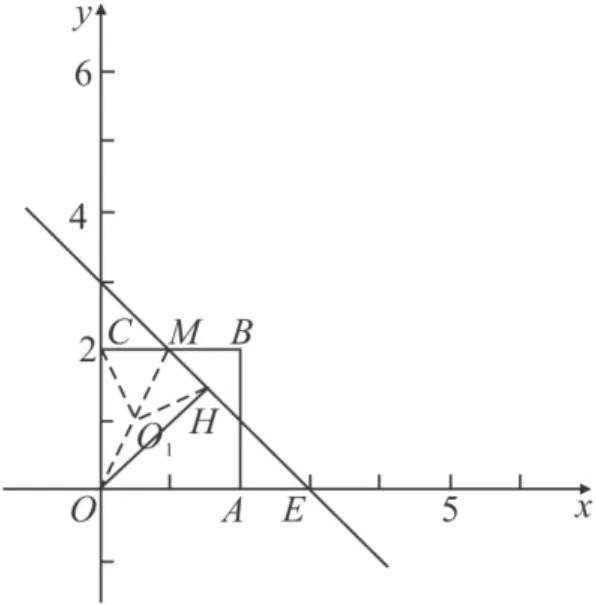
图9

点评第(3)题中垂足H为动点，求它所经过的路径的长，注意到点H是随点P从点O向点C运动而运动，关键是关注点P运动的极端位置点O和点C，得知点H的两个极端位置，再经探索知点H所经过的路径为一段圆弧，从而可求出路径长.

以上几例的共同特点是在几何图形中研究点或图形在运动中牵制形成另一相关联的动点的运动路径的长，设计新颖，不落俗套，给学习能力较强的学生创造了展示自我的空间，确保了试题在《数学课程标准》中的要求范围内具有较高的区分度和较好的效度.对这类问题要善于借助动态思维的观点来分析，不为“动”所迷惑，从特殊情形入手，变中求不变，动中求静，抓住静的瞬间，以静制动，把动态问题转化为静态问题来解决，从而找到解决问题的突破口.动与静是相对的，抓住运动中的不变量(如图形全等、距离不变等)，对比运动前后两种状态的区别，用心体会，寻找规律.教师可以通过解剖典型试题，引导学生经历解题思路的探索过程，解题方法和规律的概括过程，学会分析问题、解决问题的方法.