认知无线电中基于拟合优度的频谱盲检测算法研究

沈雷，王海泉，赵知劲，孙闽红

(1. 杭州电子科技大学 通信工程学院，浙江 杭州 310018；2. 浙江省综合信息网技术重点实验室，浙江 杭州 310027)

1 引言

在认知无线电系统中，非授权用户在频谱空闲的时候使用已经分配给授权用户的频谱，从而提高了频谱的使用效率。检测授权用户是否占用频谱，也就是频谱检测，是认知无线电系统中的一个重要问题[1]。

目前已有的频谱检测方法主要包括基于能量的频谱检测法[2～4]、基于循环谱的检测法[5,6]和基于Anderson-Darling检测法[7,8]。基于循环谱的频谱检测法利用已知授权用户的调制信息来提高频谱检测的性能，但所需样本时间长，计算复杂度高。1967年，H.Urkowitz提出了基于能量的频谱检测算法[2]，该方法不需知道授权用户的任何先验知识，近年来被广泛用到频谱检测中[3,4]。

以上叙述的方法，从数理统计的角度看，都是属于参数假设检验的范畴，即根据随机变量的某一特定参数来做假设检验。如果假设的参数估计不准，频谱检测的性能下降。例如，如果噪声方差未知，基于能量的频谱检测法性能快速下降[9,10]。

近年来，在文献[7]中提出了基于拟合优度检验的频谱检测法，可以得到比基于能量的频谱检测法更好的性能。其基本频谱检测原理是：如果授权用户没有占用频谱，则非授权用户端接收到的信号仅是高斯噪声, 从而服从零均值、方差为2σ的正态分布；另一方面，如果授权用户占用频谱，则非授权用户接收到的信号由2部分组成, 一是经过信道到达接收端的授权用户信号, 二是接收端的噪声，2种信号叠加之后，使得接收到的信号不再服从零均值、方差为2σ的正态分布。基于这一事实，频谱检测就转换为判断接收到的采样信号样本分布函数是否符合零均值、方差为2σ的正态分布函数。在文献[7]中通过度量接收到信号的经验分布和零均值、方差为2σ的正态分布之间的AD距离来判决授权用户是否使用频谱。从上面的分析可知，AD检测是基于接收信号的整个分布，而非基于某个特征参数。因此AD检测性能应该优于能量检测，并且不需要任何授权用户信号的先验知识。但遗憾的是这种算法只适合于噪声方差2σ已知情况，本文的目的是为了解决这个弱点。

为了克服以上的弱点，在文献[8]中提出了基于t分布的频谱盲检测方法。但遗憾的是，只对基于自由度为2和4的t分布频谱检测性能进行了分析，并没有给出对任意自由度 t分布的频谱盲检测性能，以及最佳自由度选择。本文首先提出一种噪声方差未知时，基于任意自由度t分布的AD检验的频谱检测算法。假设接收到的信号样本有L个，把接收到的L个样本分成N部分，每个部分有m＝L/N个数据，求其样本的均值和方差，然后求两者的比，这样可以得到一个新的序列。从统计学知识可知，这N个比值可被认为是从自由度为m的t分布的随机变量中独立得到的N个样本值。对这N个数据进行AD检测，从而判决信道频谱是否被占用。应该注意到，这种检测方法并没有用到噪声方差。基于上述原理，本文分析其频谱检测性能，并给出了最佳自由度m的选择。

其次，本文还提出了一种基于特征函数的盲频谱检测方法。由于多元AD检验并没有明确的定义，AD检测很难推广到多天线检测中。特征函数是分布函数的傅立叶变换，也能够完全描述一个信号。特征函数无论是单元还是多元都给出了明确的定义，很容易推广到多天线检测系统中。基于这种考虑，本文提出通过度量经验特征函数和已知特征函数之间的距离，在噪声方差未知的情况下，判决信道频谱是否被占用。

本文分析了所提2种频谱检测方法在衰落信道下的虚警概率和检测概率。理论分析和仿真结果都表明，所提2种算法在噪声方差未知情况下的频谱检测性能，比噪声方差已知时的AD检测性能下降1dB左右，但比噪声方差已知时的能量检测好3dB以上。在低信噪比或小样本条件下，所提2种盲频谱检测算法相比能量检测法在性能上的优点表现的更明显。

2 Anderson-Darling频谱盲检测原理

为了消除检测方法对噪声方差估计的依赖，使得噪声方差未知时，AD频谱检测算法也有效，本文引进t分布。

假设非授权用户采样了L个样本，把样本按先后顺序分成了N个不同的部分，m=L/N是每部分的样本数。M、N都是大于零的自然数。本文先对每一部分求其样本的均值和方差，然后求两者的比，这样可以得到一个新的序列：

其中，yi( i=1,2,…,N)服从自由度为m-1的t分布，由文献[11]可知，自由度为m-1的t分布的概率密度函数记为

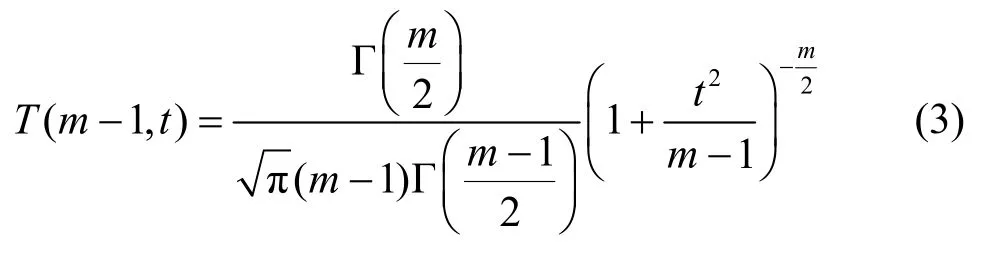
Γ是伽玛函数，其累积分布函数记为G0,m(y),则其值为

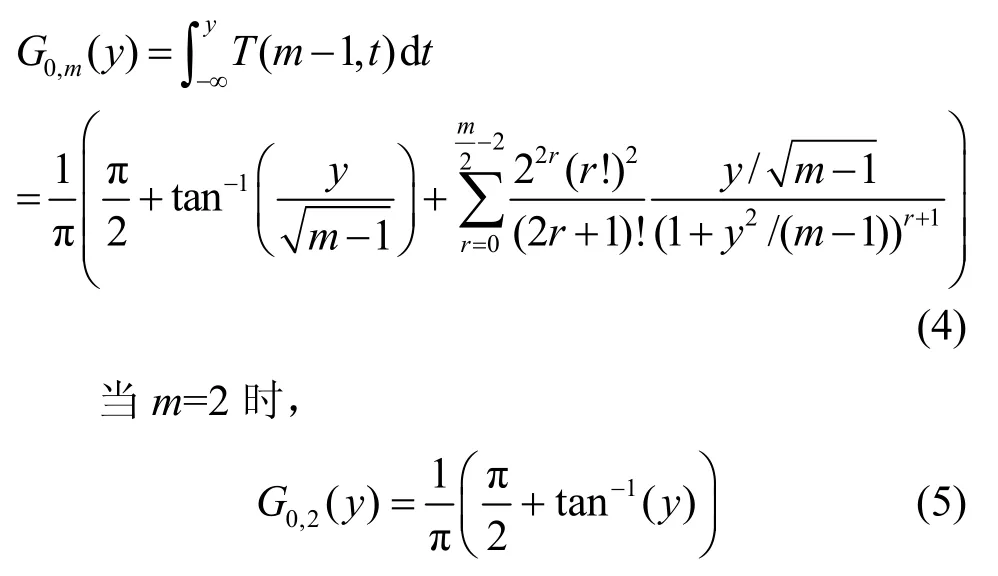
如果授权用户存在，由于授权用户信号的调制特性以及信道的传输特性，非授权用户端接收的样本不再是均值为0，方差为2σ的高斯噪声。因此m个样本的均值和方差比yi也不服从自由度为m-1的t分布，从而样本yi一般不服从分布G0,m(y)。基于这一事实，认知无线电系统中频谱检测就可以等价于下列假设检验。

H0：授权用户接收样本是统计独立的变量，服从分布G0,m(y)。

很显然，如果H0不成立，样本yi不服从分布G0,m(y)，表明非授权端接收到的信号不是均值为0，方差是σ2的高斯噪声, 从而说明信道中存在授权用户信号的传输。相反，如果H0是成立的，样本yi服从分布G0,m(y), 表明非授权端接收到的信号均值为0，方差是σ2的高斯噪声，信道中不存在授权用户信号的传输。

为了对这个假设进行检验，从上面的分析可以知道，引进t分布以后，在m给定情况下，G0,m(y)的分布是已知的，可以用Anderson-Darling检验进行检测。其具体方法如下，首先对所有新的样本序列按小到大排列，这里假设y1≤y2≤…≤yN，利用这些样本，当每个部分有m个数据时，定义经验分布函数为GN,m(y)，具体如下：

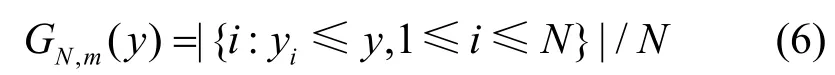
如果信道中没有授权用户传输，那么H0假设是成立的，由大数定理，如果N趋向无穷大，GN,m(y)必然趋向于G0,m(y)。如果信道中存在授权用户传输，那么H0假设是不成立，即使当N趋向无穷大时，GN,m(y)不会趋向于G0,m(y)。

由上面的分析，可以利用GN,m(y)与G0,m(y)之间的差别进行信号频谱检测。通常情况下，上述差异的大小是用2个分布之间的距离来度量，如果距离大于某个门限，则假设H0不成立，信道中存在授权用户传输；反之，如果距离小于某个门限，则接收假设H0，认为信道中只存在噪声，不存在授权用户信号的传输。

在文献[12]中，AD检测是基于分布间的距离定义，其具体定义如下：

这里φ(u)=(u(1-u ))-1。式(7)的计算可以简化为[12]

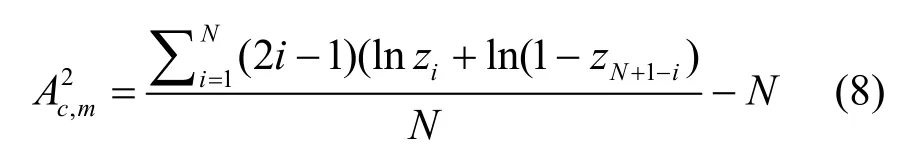
其中，zi=G0,m(yi),i=1,2,…,N 。为了得到门限值，一般情况下需要的分布函数。文献[12]给出了一个当N趋向无穷时的渐近分布，具体的分布函数为

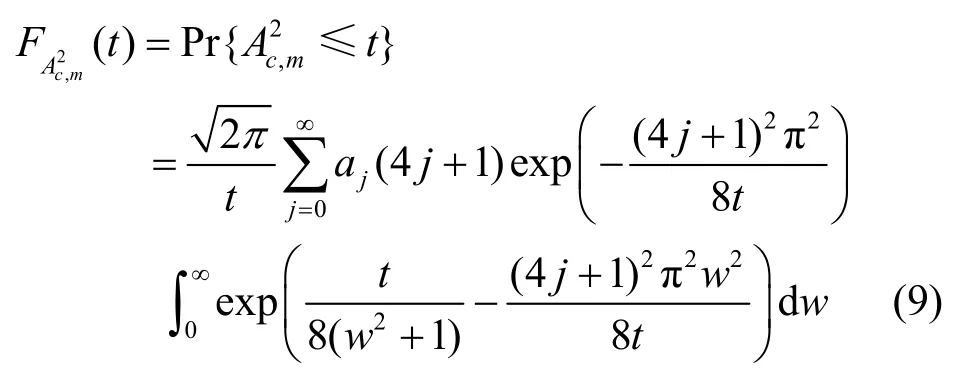
其中， aj=(-1 )jΓ( j + 0 .5)/(Γ(0.5)j!)，对于某个给定的虚警概率α，其门限值t0可由式(10)决定：

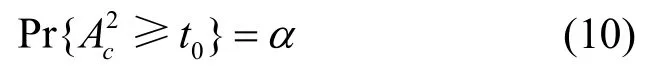
3 基于特征函数的频谱盲检测原理

由于特征函数可以完整地描述随机变量，可以通过度量特征函数的距离来进行频谱检测，其具体方法如下。

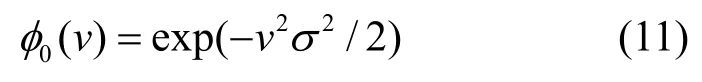
当信道中存在授权用户信号传输时，由于受信号调制特性和信道传输特性的影响，X不服从均值为零，方差为2σ的高斯正态分布，此时其特征函数也不服从φ0(v)。这样，基于特征函数的频谱检测可以等价于下列假设检验。

很明显，如果 H0成立，则表明信道中不存在授权用户传输；如果 H0不成立，则表明信道中存在授权用户的传输，信道频谱被占用。

文献[14]中为了检验信号的高斯性，定义了经验特征函数。根据相同的原理，进行信号频谱检测，此处定义X的经验特征函数为

假如信道中不存在授权用户传输，则L趋向无穷时，经验分布趋向于高斯正态分布，因此，φL(v)趋向φ0(v)。而当信道中存在授权用户传输的时候，φL( v)不趋向φ0(v)。所以通过度量经验特征函数φL( v)与特征函数φ0(v)的距离，可以用来判决是否存在授权信号的传输。这里令特征函数距离统计特征量为

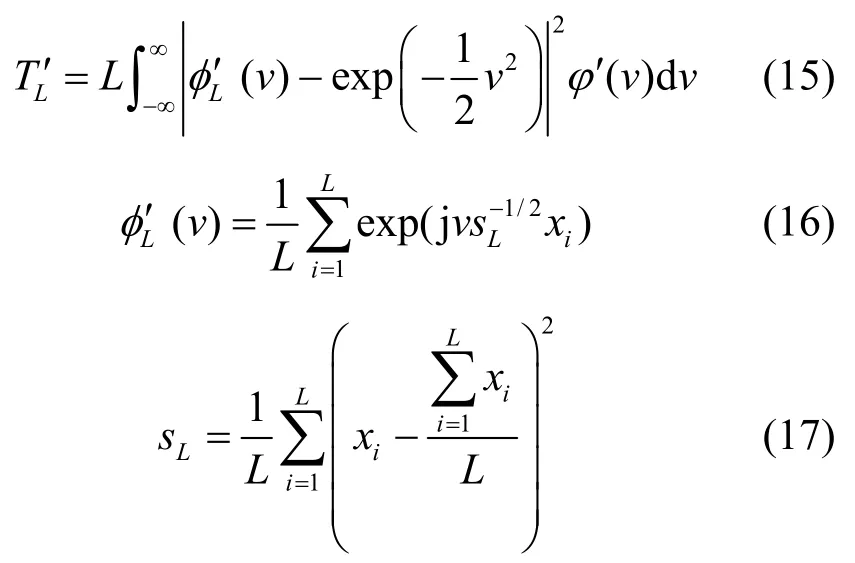
对式(15)的积分进行展开，可以得到TL′的简明计算公式为

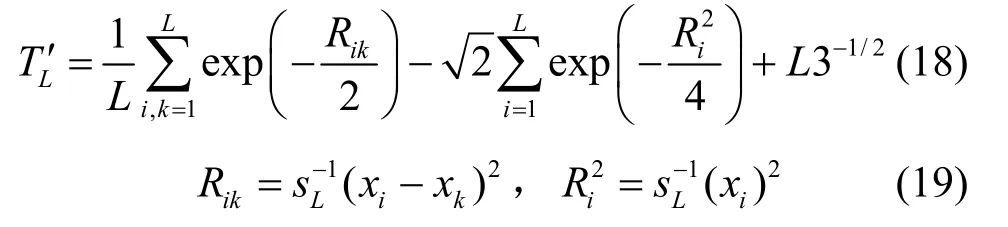
信道噪声方差未知情况下，基于特征函数的频谱盲检测等价于下面的假设检验：

这里t0表示检测门限，可通过式(18)～式(19)仿真得到。如果 TL′ ＞t0，表明经验特征函数 φL′(v)与φ0′(v )距离很远，因此拒绝假设检验 H0，认为信道中存在授权信号的传输。否则，表明经验特征函数φL′(v ) 与φ0′(v)距离很近，假设检验H0成立，认为信道中不存在授权用户信号的传输。

通过Monte Carlo仿真的方法，表1给出了不同虚警概率下，不同采样样本个数下的特征函数盲检测方法的门限。从表1可知，在虚警概率为0.05和0.01时, 当样本L大于50时，门限t0已不随样本个数的变化而变化，这是由于此时 φL′(v)与exp(-v2/2)已经足够近似。

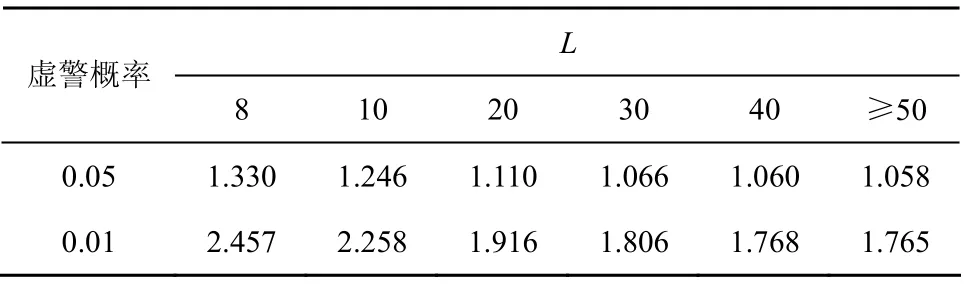
表1 特征函数盲检测门限与虚警概率

4 Anderson-Darling频谱盲检测概率分析

频谱检测概率是衡量频谱检测方法性能的一个重要参数。本节分析噪声方差未知时，衰落信道下AD检测的检测概率，在授权用户信号存在时，接收到的信号样本可以表示为

其中，c表示所传送的信号，传输的信号一般是复数，但复数可以表示成实部和虚部的和，如果把实部与虚部分别来考虑，则可以假设c为实数。并且在下文中，始终在实数范围内来考虑问题。不失一般性，这里假设c=1。wi是服从标准正态分布的变量，2σ是噪声的方差，h表示衰落因子，服从标准正态分布。假设信道是平稳慢衰落的，基于这一假设，可以假定在得到样本 x1, x2,… ,xL的过程中，h始终是一个常数，但在得到下面L个样本时，h可以变为另外一个常数。h的这个变化是服从标准正态分布的。在信号存在情况下，式(1)可以重新写为

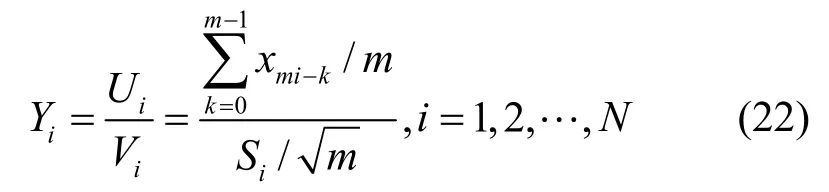
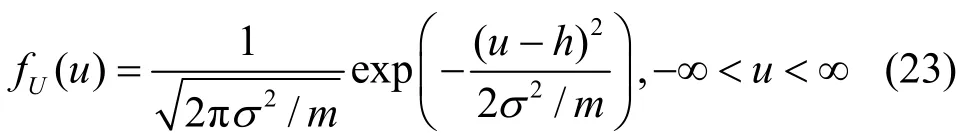
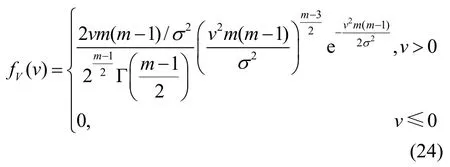
在式(23)和式(24)的基础上，可以得到Yi服从累积分布函数：

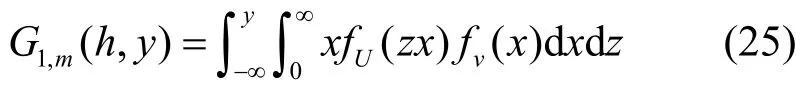
当m＝2时，累积分布函数可以写为

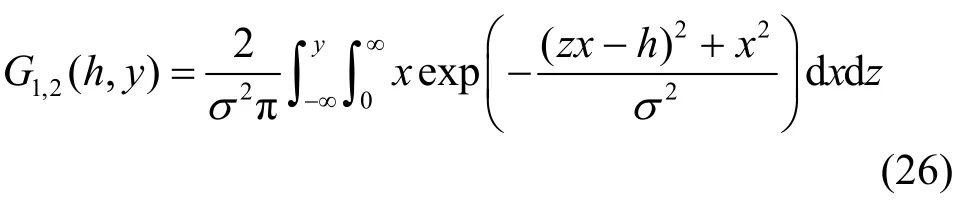
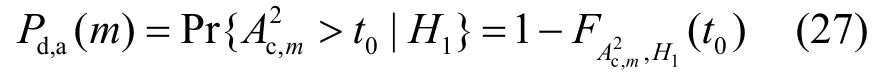
假设接收到的信号样本 y1≤ y2≤ … ≤ yN，每个样本都是m个X样本的均值和方差比，GN,m(h, y)是衰落因子为h时候的信号样本 y1≤y2≤…≤yN的经验分布函数；授权用户传输信号存在时，当N趋向无穷时， GN,m(h, y)应逼近 G1,m(h, y)。

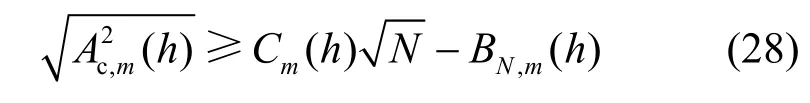
其中，

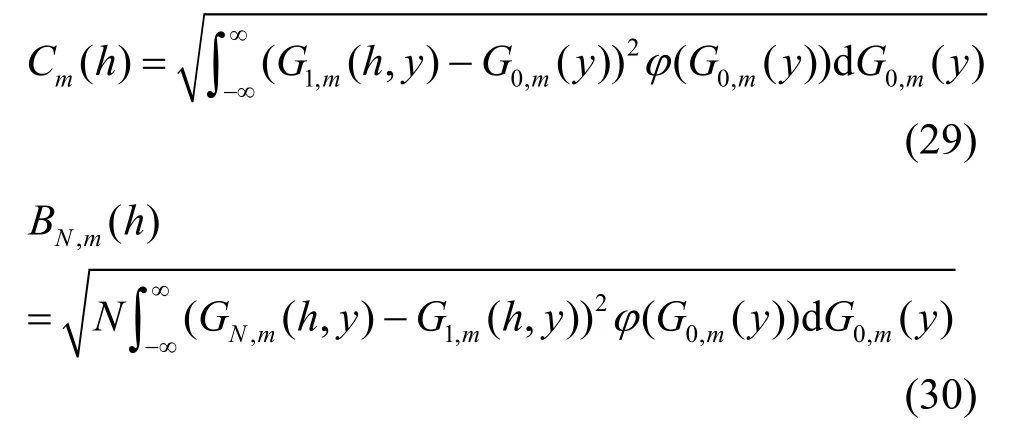
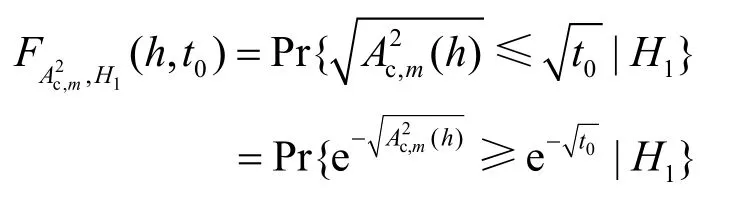
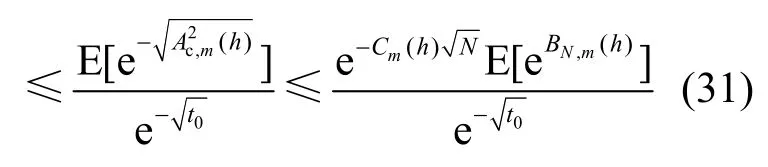
式(31)中第1个不等式是马尔可夫不等式得到，而第2个不等式是式(30)得到。期望均值的大小和样本值和衰落因子h相关。式(31)可以表示为

在m，h给定条件下，AD检测的检测概率Pd,a(m, h)的下界为

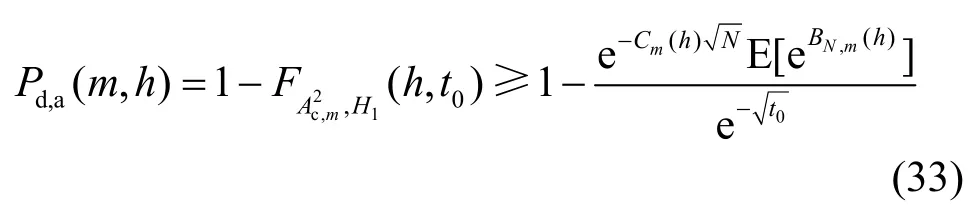
由式(29)计算，如果在m，h给定，Cm(h)是一个大于零的常数；文献[13]证明在H1假设下，当N-＞∞，(h)有界分布，则也是有界的。由式(31)～式(33)可知，对于给定的门限t0，随着采样样本数N增加，趋向于0，检测概率Pd,a(m, h)趋向于1，变化的速率为

瑞利衰落信道下，h服从标准正态分布, 由式(32)和式(33)，如果门限t0、m给定，基于AD的频谱盲检测的平均检测概率下界为

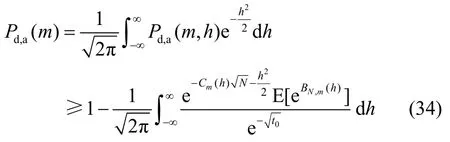
平均检测概率是Pd,a(m, h)的加权积分，随着样本数N增加，检测概率Pd,a(m)也趋向于1。

5 基于特征函数的频谱盲检测检测概率分析

在本节中，将给出基于特征函数的频谱盲检测的性能。在信道中存在授权用户传输的时候，给定衰落因子h，其检测概率为

由式(22)可以知道，当信道中存在授权用户传输，L趋向无穷大，φL′(v)趋向于φ1′(v)=exp(jvh/σv2/2)。类似于式(28)～式(33)的分析过程，可以得到基于特征函数的频谱检测概率的下界为

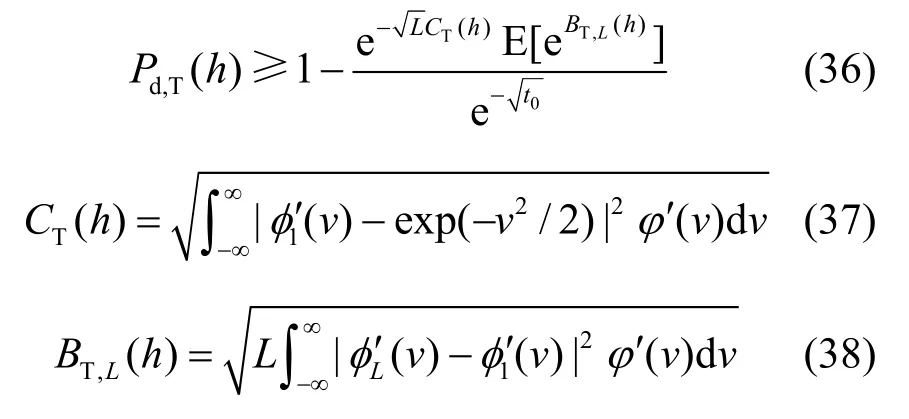
很明显，在h给定的情况下，CT(h)是一个固定的常数，根据文献[13]，当L-＞∞，(h)有界分布，则也有界。当L趋向无穷大的时候，检测概率Pd,T(h)以最小的速度趋向于1。

由于瑞利衰落因子服从标准正态分布，在设定门限t0后，基于特征函数频谱检测的平均检测概率下界为

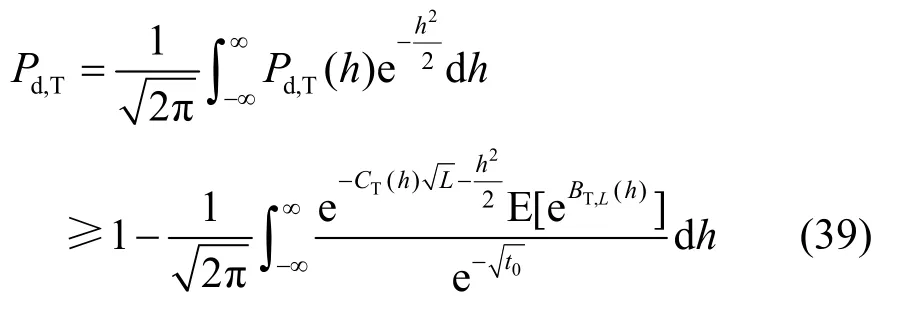
当样本L趋向无穷大时，平均检测概率Pd,T同样趋向于1。

6 仿真结果与分析

为了验证理论分析的结果，本节将给出Matlab环境下的仿真结果。具体的仿真环境如下：假设信道是瑞利慢衰落，噪声方差是未知的。对基于AD频谱盲检测算法和基于特征函数的频谱盲检测算法的检测概率做了仿真。为了比较，同时对噪声方差已知时，瑞利衰落信道下AD检测概率[7]和能量检测的检测概率做了仿真。在仿真中只对信号的实部进行处理，此时衰落因子h服从标准高斯正态分布，不失一般性，这里假设发射信号C=1。

图1给出了虚警概率a=0.05，采样样本数L=32时，不同信噪比下，衰落信道下各种检测方法仿真值的比较。噪声方差已知时，AD检测[7]的检测概率比能量检测概率提高大约4dB。本文提出的噪声方差未知时的AD盲检测性能比噪声方差已知时的AD检测性能有所下降(性能下降在1dB以内)，但比噪声方差已知时的能量检测提高了3dB以上。噪声方差未知时，采样点数L=32时，样本分成8部分，每部分m=4时的检测性能比样本分成16部分，每部分m=2更接近噪声方差已知时的AD检测性能。本文提出的噪声方差未知时，基于特征函数盲检测算法性能与AD盲检测性能相近。这2种盲检测方法都不需要噪声方差的先验知识，克服了能量检测方法在噪声方差未知时，检测性能急剧下降的缺点。

图1 衰落信道下各种方法检测概率比较

图 2给出了虚警概率 a=0.05，采样样本数L=64时，自由度m取不同值时的AD盲检测性能分析。从图 2可以得到，m=2的时候，AD盲检测性能最差，随着m值的增大，AD盲检测性能提高，m=32时，AD盲检测性能与噪声方差已知时的AD检测性能接近。一方面随着m的增加，n值减少，AD检测性能下降。另外一方面，由于自由度 m值增大，t分布更快速地趋近于高斯分布，也就是逼近噪声方差已知时的AD检测。可见，随着自由度m的增大，AD盲检测的性能提高。从以上的仿真结果可以看出，在采样样本数L给定的情况下，选择自由度 m=L/2，盲检测性能最好。

图2 不同自由度AD盲检测性能分析

从图2和图3的比较可以得到，采样点个数增大，检测概率的性能提高。在同样采样点个数下，所提2种检测算法基于AD的频谱检测算法和基于特征函数的频谱盲检测算法性能比能量检测性能好。

图3 各种检测方法工作区间特性分析

为了进一步对本文所提2种盲检测方法和能量检测的性能进行比较，图3给出了信噪比为6dB，采样样本数L=32，AD检测、AD盲检测、基于特征函数的盲检测和能量检测的工作区间特性。可以看到，AD检测比能量检测具有更理想的工作区间特性，AD检测概率更快速的逼近 1。噪声方差未知时的AD盲检测比噪声方差已知时的AD检测工作区间特性略有下降，但比噪声方差已知时的能量检测性能好。基于特征函数的盲检测性能与AD盲检测性能接近。在虚警概率要求较低时，AD盲检测和基于特征函数盲检测比能量检测具有更高的检测概率。

7 结束语

本文提出了认知无线电系统中，基于Anderson-Darling的频谱盲检测方法和基于特征函数的频谱盲检测方法。这2种方法不需要授权用户信号的先验知识，而且克服了Anderson-Darling检验和能量检测对噪声方差先验知识的要求。本文分析了衰落信道下，所提2种盲检测方法的虚警概率和检测概率，并与传统的能量检测性能做了比较。理论和仿真表明，AD盲检测和特征函数盲检测相比传统的能量检测，具有更好的性能。

[1] MITOLA J, MAGUIRE G Q. Cognitive radio: making software more personal[J]. IEEE Personal Commun Mag, 1999, 6(4): 13-18.

[2] URKOWITZ H. Energy detection of unkown deterministic signals[J].Proceedings of the IEEE, 1967, 55(4): 523-531.

[3] KIM S, LEE J, WANG H, et al. Sensing performance of energy detector with correlated multiple anetennas[J]. IEEE Signal Processing Letters, 2009,16(8):671-674.

[4] DIGHAM F, ALOUNINI M, SIMON M K. On the energy detection of unknown signals over fading channels[J]. IEEE Trans Commun,2007,55(1): 21-24.

[5] DU K L, MOW W H. Affordable cyclostationarity-based spectrum sensing for cognitive radio with smart antennas[J]. IEEE Transations on, Vehicular Technology, 2010,59(4): 1877-1886.

[6] LUNDEN J, KASSAM S A, KOIVUNEN V. Robust nonparametric cyclic correlation-based spectrum sensing for cognitive radio[J]. IEEE Transactions on Signal Processing, 2010, 58(5): 38-52.

[7] WANG H Q, YANG E H, ZHAO Z J, et al. Spectrum sensing in cognitive radio using goodness of fit testing[J]. IEEE Transactions on Wireless Communications, 2009, 8(11): 5427- 5430.

[8] SHEN L, WANG H Q, ZHANG W, et al. Blind spectrum sensing for cognitive radio channels with noise uncertainty[J]. IEEE Transactions on Wireless Communications, 2011, 10(6):1721-1724.

[9] SONNENSCHEIN A, FISHMAN P M. Radiometric detection of spread-spectrum signals in noise of uncertain power[J]. IEEE Trans Aerosp Electron Syst, 1992,28(3): 645-660.

[10] TANDRA R, SAHAI A. Fundamental limits on detection in low SNR under noise uncertainty[A]. Proc IEEE Int Conf Wireless Networks,Commun And Mobile Computing[C]. Maui, Hi, 2005. 464-469.

[11] GOSSET W S. The probability of a mean[J]. Biometrika,1908.1-25.

[12] ANDERSON T W, DARLING D A. Asymptotic theory of certain“Goodness of Fit”, criteria based on stochastic processes[A]. The Annals of Mathematical Statistics[C]. 1952, 23(2): 193-212.

[13] STEPHENS T W. EDF statistics for goodness of fit and some comparisons[J]. Journal of the American Statistical Association, 1974,69(347):730-737.

[14] EPPS T W, PULLEY L B. A test for normality based on the empirical characteristic function[J]. Biometrika,1983, 70(3):723-726.