认知无线多跳网中保证信干噪比的频谱分配算法

孙杰，郭伟，唐伟

(电子科技大学 通信抗干扰技术国家级重点实验室, 四川 成都 611731）

1 引言

认知无线电（CR, cognitive radio）的概念最早由Joseph Mitola III于1999年提出[1,2]，旨在解决目前使用固定频谱分配方式造成无线频谱资源使用紧张且利用率低下的问题[3]。认知无线电技术已经成为当前无线通信技术的研究热点之一[4～12]，一些相关的国际标准草案也在不断提出与讨论之中，如IEEE 802.22[13,14]，IEEE 802.16h[15]，IEEE 802.11s[16]等。

动态频谱分配（DSA, dynamic spectrum allocation）是认知无线电中最重要和最关键的技术之一，主要分为overlay和underlay 2种分配方式。前者仅允许次用户在主用户空闲时才能使用频谱；后者允许次用户与主用户同时使用频谱，但次用户对主用户的干扰功率不能超过一定限制。

目前对认知无线电动态频谱分配的研究主要集中在蜂窝网络中[4～8]，对其在无线多跳网络环境下的研究相对较少[11]。众所周知，在单一频谱或固定多频谱条件下，无线多跳网络的分布式特性使得信道冲突问题成为巨大的挑战。认知无线电技术为解决这一问题提供了新的思路，同时也为无线多跳网络的研究开拓了新的空间。

目前对underlay方式下频谱分配的研究以总的干扰功率为指标进行考虑[4,5]。然而，传输性能的好坏实际取决于接收信干噪比（SINR, signal to interference plus noise ratio），而不仅仅是总的干扰功率。节点的发射功率与接收到的干扰功率二者往往互相耦合，低的干扰功率并不一定意味着高信干噪比。更多的研究是以信干噪比（或其函数，如信道最大传输率等）作为衡量指标[6～8]。一般使用优化理论或博弈论等数学工具来最大化节点或者系统总的信干噪比。此类算法尽管以最大化信干噪比为目标函数，然而并不能满足节点最低接收信干噪比的要求，且不一定能够实现分布式算法。如果网络中需要分配频谱的次用户较多，而最低信干噪比要求较高，那么这些算法无法保证有效通信。

本文针对多主用户（频谱）多次用户环境下的无线多跳网络，设计了一种适合underlay方式的频谱分配算法，同时实现信道与功率2个层面的分配。该算法在保证次用户总干扰功率不超过主用户干扰限制的同时，能够满足次用户间无线传输最低接收信干噪比的要求。以该算法为基础，次用户之间可以实现信干噪比有保障的数据传输。

在下文中，第2节首先给出本算法适用的网络场景及系统模型，第3节将给出算法的详细步骤及相关证明，第4节通过仿真验证本文算法的有效性，第5节是结束语。

2 网络场景与系统模型

本文将频谱分配分为2个层面：1）信道分配：即不同可用频段的分配，假设不同信道间相互正交；2）功率分配：同一信道下多个次用户间的功率分配。

本文考虑多主用户（频谱）多次用户并存的认知网络环境。设共有M个主用户，每个主用户只有一个可用频谱，即共有M个可用信道。所有信道相互正交（不考虑邻道干扰），且信道具有对称性（双向的信道增益相等）。为表述方便，次用户成对出现且配对固定（一跳内接收节点选择属路由问题）。前一用户对的接收节点作为下一用户对的发送节点，次用户端到端多跳传输即可视为在多个次用户对间依次传递。不考虑移动性。设需要进行频谱（信道、功率）分配的次用户共有N对（即N跳），每对次用户在同一时刻仅能选择一个信道。

在underlay方式下，同时考虑主用户干扰限制和次用户接收信干噪比要求，则次用户的发射功率必须满足以下2点。

第1点，所有次用户总的发射功率受限。本文沿用美国联邦通信委员会（FCC, Federal Communications Commission）定义的“干扰温度”来表征这一限制[17]，并假设所有可用信道的带宽是固定且已知的。干扰温度上限的等效数学表达式如式(1)所示：

其中，pi是次用户对i的发射功率，ck表示第ck个信道，hick表示从次用户对i到主用户的信道增益注1注1 在实际系统中可能为从次用户到若干测量点的信道增益。具体干扰对象的考虑，可以为主用户发送节点，也可以为主用户接收节点，本文不加区别。，Tck表示总的功率限制。

第2点，所有次用户对的接收信干噪比须大于等于一定阈值Γi。如式(2)所示：

其中，N0为背景噪声，Pck为主用户ck的发射功率。hii表示次用户对i收发节点之间的信道增益，hji表示从次用户对j的发送节点到次用户对i的接收节点的信道增益。

在下文，将设计一套信道、功率联合分配算法，实现次用户之间信干噪比有保证的通信。这样做的好处是：1）如果每个次用户只装备一套收发机，则可以解决暴露终端问题（各对次用户的信干噪比始终是被保证的）；2）如果每个次用户装备2套收发机，配合一定的控制协议则可以实现全双工通信，如图1所示；3）不同的信干噪比下限Γi决定了不同最大数据传输率，通过改变Γi可以实现对不同数据传输率QoS要求的支持。

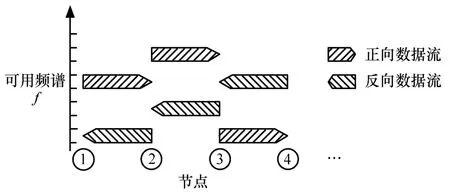
图1 可实现全双工的频谱分配

3 保证信干噪比的信道-功率联合分配算法

多信道条件下的多次用户频谱分配问题，一般采用优化理论或博弈论等方法求解。考虑到应尽可能减少主用户的参与，以及在实际应用中信道增益参数不易获取，在本文场景中采用优化理论是不合适的。博弈论更适合于分布式系统，但有时只能得到次优解。本文利用博弈论提出一种联合信道与功率的频谱分配算法，其结果虽不是最优的（如以总功率、总信道利用率等进行度量），却是一种行之有效的方法。

3.1 信道分配算法

考虑对次用户总发射功率的限制，规定次用户须先向主用户提出频谱分配申请，得到主用户批准才能使用其频谱。在实际系统中可通过收费等手段实现。假设主用户在正常传输中专门划出特别时隙（或专门的认知导频信道）用于接收次用户频谱分配申请。主用户在该时隙内广播自身中心频率、频谱带宽、干扰温度上限等信息。次用户监听这些信息，在有数据传输需要时选择某一主用户向其发出频谱分配申请。只有在这特殊的时隙内，次用户不受总功率限制可与主用户通信。由于主用户只具有单一频谱，同时次用户是分布式的，因而此时适合使用CSMA/CA方式接入。这意味着在同一时间只能有一个次用户与主用户通信。这为总功率受限的实现提供了便利。次用户选择信道，同时满足总的发射功率受限的算法如下。

步骤1 次用户对i监听各主用户的中心频率fck、频谱带宽B、干扰温度上限TL(fck,B)、发射功率等参数，按Tck=κBTL(fck,B)计算总的发射功率限制Tck。其中，κ为玻尔兹曼常数。

步骤2 次用户对i选择Tck值最大的信道ck作为自身的信道，向其主用户发出频谱分配申请。

步骤3 次用户对i根据主用户的发射功率参数计算与主用户之间的信道增益hick。将Tck/hick作为自身发射功率的上限，即发射功率取值范围为[0,Tck/hick]。

步骤4 次用户对i按照本文功率分配算法计算自身发射功率pi。

步骤5 主用户测量当前的干扰温度TI，如果TL-TI＜0，则拒绝次用户对i的频谱分配申请；如果TL-TI=0，则仍接受i的申请，但此后关闭参数广播，不再接受新的频谱分配申请；如果TL-TI＞0，使用TL=TL-TI更新干扰温度上限值，回到步骤1。

3.2 功率分配算法

3.2.1 功率博弈模型

为保证满足主用户的干扰限制，次用户在功率分配时必须以在信道选择时获得的Tck/hick作为发射功率上界，然后与同一信道上其他次用户进行非合作博弈，最终选定满足最低信干噪比的功率。

将次用户对i确定发射功率pi的过程建模成完全信息静态非合作博弈GP=＜N, {Si}, {Ui}＞。其中，N为博弈者，即次用户对集合；Si为次用户对i的策略集，即发射功率取值范围，Si=[0,Tck/hick]；Ui为次用户对i的收益函数，定义如式(3)所示：

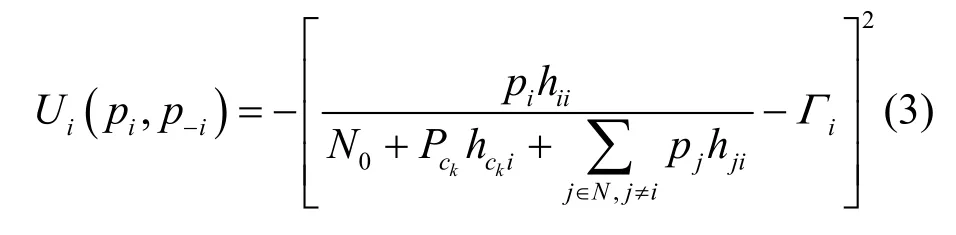
其中，p-i指除pi以外的其他次用户发送功率的集合。

使用这样的收益函数的意义如下。1）每个次用户将选择最接近自身信干噪比要求的发射功率。在满足信干噪比要求的条件下实际降低了发射功率，达到了节能的效果。如果直接将信干噪比（或者其单增函数）作为收益函数，博弈结果只会使所有次用户使用最大功率进行发射[6]，其虽然在数学上是帕累托最优的，但是显然不是实际可行的方案。2）如果需要更高的信干噪比，次用户可以通过改变自身Γi值来灵活实现。在其他一些算法（如拍卖算法[7,8]，VCG算法[9,10]，Stackelberg算法[11,12]等）中无法实现最低信干噪比的要求，并同时兼顾灵活性。

定理1 GP存在纯策略的纳什均衡点且唯一。即算法有解且唯一。

证明 Si=[0,Tck/hick]是实数域R上的紧致凸集。易验证∂2Ui/∂pi2＜0对任意s-i∈S-i都成立，因此可推出Ui是si∈Si的连续凹函数。由Debreu-Fan-Glicksberg不动点定理[18]可知，GP至少存在一个纯策略的纳什均衡点。

下面证明唯一性。将Ui对pi求一阶导数，并令其等于0，可得：

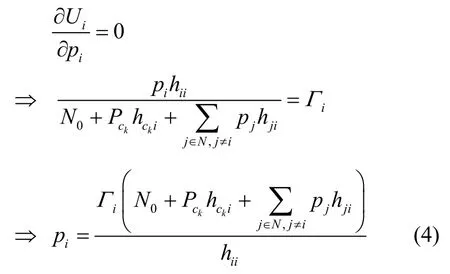
由文献[19]可知，因为∀i∈N，Ii(p)=都满足以下3点，所以博弈Gp拥有唯一的纳什均衡点，其中p={p1, p2,…,pn}。

a) 正数性（positivity）：Ii(p)＞0。

b) 单调性（monotonicity）：如果p≥p′，则有I( p)≥I( p′)。

c) 伸缩性（scalability）：∀α＞1，均有αI( p)＞I(αp)。

3.2.2 功率分配的分布式迭代算法

3.2.1节证明了次用户功率博弈Gp具有唯一的纳什均衡点，但如何求解该纳什均衡点是另一个重要问题。如果直接对所有次用户的收益函数求一阶导并令其等于0，Gp的纳什均衡点并不难求得。可以通过求解式(5)的线性方程组来计算得到。

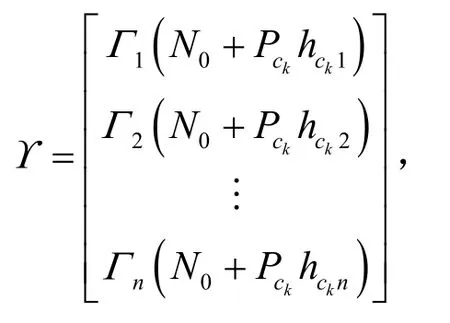
但是，由于有发送功率上界的限制，功率博弈Gp本身并无法保证博弈结果一定大于等于Γi，因此只是尽可能接近。同时，式(5)的求解假设了任意节点间的信道增益hij是已知的，这一要求在实际网络中很难实现。因此，本文提出一种分布式迭代算法，使得各次用户在仅需测量自身信干噪比的条件下收敛到Gp的纳什均衡点，且该均衡点恰好使得各次用户信干噪比等于Γi。

证明 从定理1的证明及纳什均衡点的定义可知，次用户对i调整发射功率应使得自身的信干噪比逐渐逼近Γi。即在第t次迭代中，有

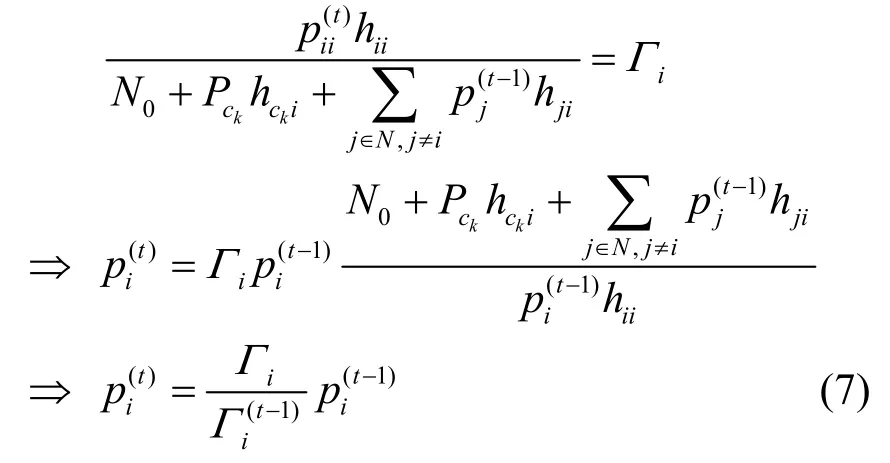
直接按照式(6)迭代能够得到Gp的纳什均衡点，但该均衡点不一定满足最低信干噪比要求。因此，制定以下算法实现各次用户对的最终迭代结果等于Γi：

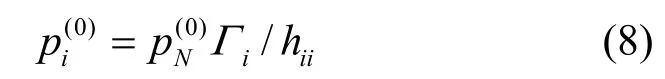
步骤5 事先设定最大迭代次数T（或者最长迭代时间），以及允许的信干噪比迭代误差ε，如果在T次迭代内，则退出功率选择，选择其他可用信道。回到信道分配算法。

4 仿真及分析

4.1 仿真网络场景

为验证算法的有效性，本文使用 MATLAB进行仿真实验。使用的网络场景如下。

10对次用户随机分布在1 000m×1 000m的范围内。场景内总共有1～20个主用户，根据仿真需要出现的数目不等，位置随机。每个主用户只有一个可用频谱，且不同频谱相互正交。假设各频谱除中心频率外，干扰温度上限、频谱带宽等都相同。节点间信道增益按照FreeSpace无线传播模型进行计算。为简便起见，所有次用户对的最低信干噪比要求Γi统一设为1，信干噪比迭代误差ε除特别说明外都为0.001，最大迭代次数为100。每个仿真结果均为同一条件下多次仿真的平均值。

4.2 仿真结果及分析

本文算法的典型迭代过程如图2所示。图2(a)是当某次用户对已经达到纳什均衡后，又有新的次用户对陆续加入同一信道，造成新的功率博弈，重新开始新的迭代并最终收敛的过程。从图中可以看出，更高的信干噪比迭代误差要求将导致更多的迭代次数。但总体来说，本文所提算法具有较好的收敛速度。通过大量仿真实验，当信干噪比迭代误差要求为0.001时，本文算法基本能在100次迭达内达到收敛。图2(b)所示是当次用户在首次选择的信道中，在规定迭代次数内无法满足信干噪比迭代误差要求时，将重新选择其他信道开始新的博弈，最终达到纳什均衡的过程。从图中可以看出，在无法达到收敛时，次用户会很快迭代到最大功率，在加大干扰其他次用户的同时并无法提高自身信干噪比。当找到能够收敛的信道时，最终的发射功率值反而有所下降。

图3所示为随着次用户的增多，主用户所受到的干扰功率。干扰功率会随着次用户数量的增加而加大是必然的，但本文的迭代算法保证了这种变化是平坦的。同时使得次用户不会为了更高的信干噪比而无限制提高发射功率，陷入如文献[6]中的“发射功率陷阱”。相反，次用户会合理地控制发射功率，其实际效果反而会提高信干噪比（如图 2(b)所示）。当次用户过多，总的干扰超过主用户的干扰限制时，最后一个次用户将不被允许接入该信道，以保证对主用户干扰限制的满足。这一点由3.1节的信道选择算法保证。这也是图3中曲线最后先上升再下降的原因。

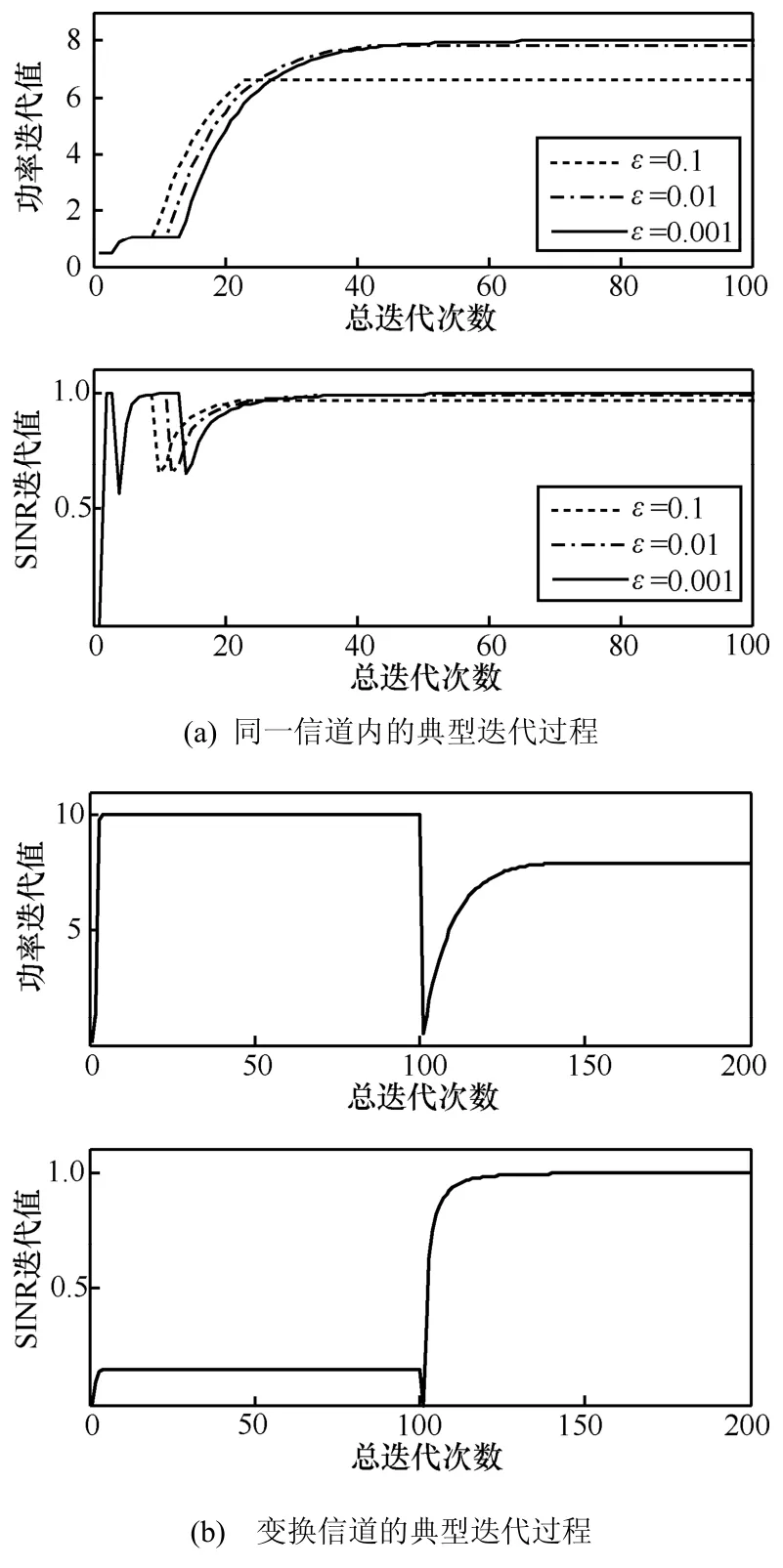
图2 执行算法的典型迭代过程

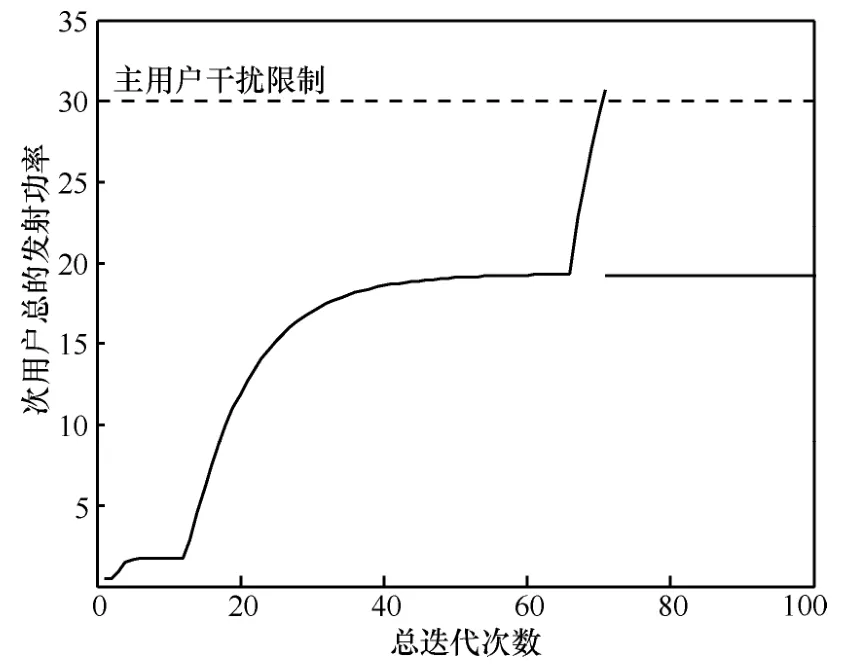
图3 主用户所受干扰

图4所示为次用户平均迭代次数随可用信道数变化的仿真结果。图中每条曲线都是多次随机节点分布仿真结果的平均值。从仿真结果可以看出，当可用信道数较少时，多个次用户竞争同一信道，将导致更多的迭代次数；当可用信道数较多时，一个信道下包含较少次用户，因而很快得到收敛。3.1节的信道选择算法保证次用户将选择具有最大干扰功率限制的主用户，从而使次用户尽可能地分散到不同的信道中。这样一方面减少了干扰，另一方面也避免了多个次用户集中在同一主用户下，造成总迭代次数过多的情况。

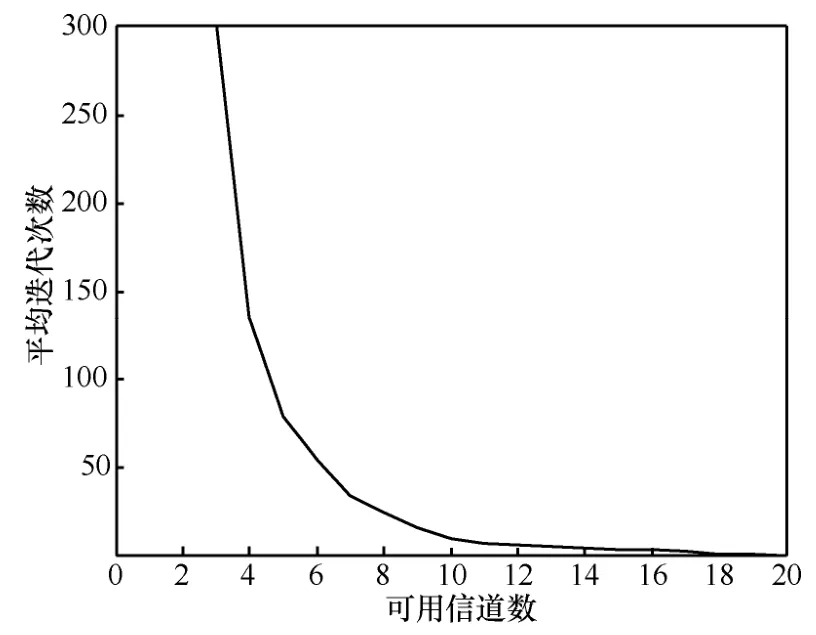
图4 次用户平均迭代次数

图5所示为在不同的可用信道数目的情况下，次用户在收敛到合适的发射功率之前平均需要变换信道的次数。在本文的算法设计中，主用户不能无限制容纳任意数目的次用户。能够成功进入某主用户信道并最终在功率博弈中收敛的次用户，必须满足总功率受限和最低信噪比要求2个要求。当次用户在某一个信道内进行功率博弈无法收敛时，将跳变到另一个信道开始新的博弈。因此，当总的可用信道数较少时，一个次用户可能需要经过多次频率跳变才能最终找到能够满足自身信干噪比要求的信道。从图中可以看出，合理设置可用信道数将能够极大减小次用户信道跳变的次数。

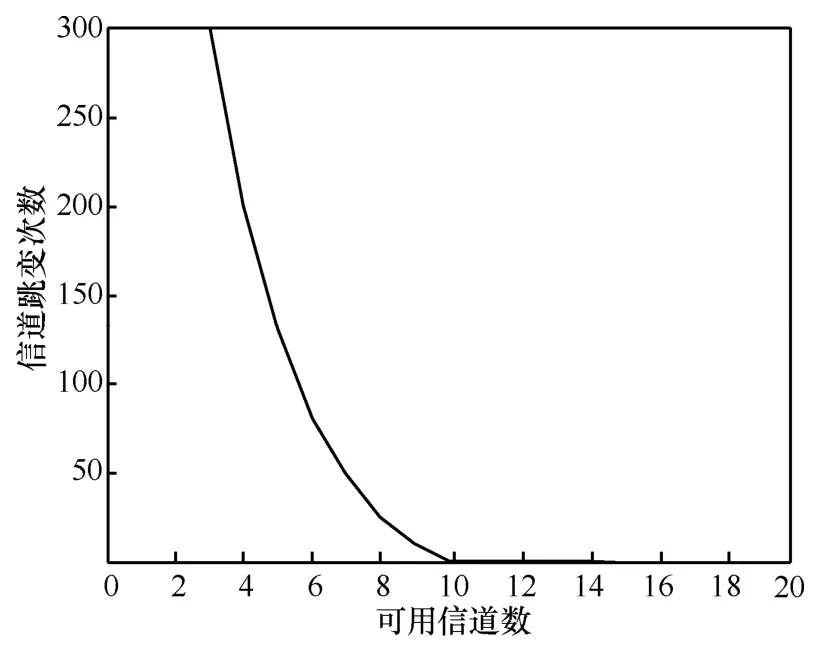
图5 次用户信道跳变次数

5 结束语

动态频谱分配技术的运用，为无线多跳网络的研究发展提供了新的空间。但同时，由于频谱资源可能随着时间的流逝发生变化，使用不同频谱的节点间如何通信等问题还需要深入研究。在本文所提出的频谱分配算法的基础上，如何设计高效合理的信道接入控制协议，实现不同频谱节点间的通信将是下一步工作的重点。

更进一步，由于算法中节点可以根据需要改变自身的最低信干噪比要求——最大信道传输率，因此可以制定专门的控制信令，让网络中的特定节点具有所需要的最大信道传输率，从而实现某些QoS指标的端到端重构。这将是今后工作长期关注的研究方向。

[1] MITOLA J, MAGUIRE G Q. Cognitive radio: making software radios more personal[J]. IEEE Personal Communications, 1999, 6(4):13-18.

[2] MITOLA J. Cognitive Radio: An Integrated Agent Architecture for Software Defined Radio[D]. Royal Institute of Technology, 2000.

[3] FEDERAL C C. Notice of Proposed Rule Making and Order[R]. ET Docket No 03-322, 2003.

[4] LA Q, CHEW Y, SOONG B H. An interference minimization game theoretic subcarrier allocation algorithm for OFDMA-based distributed systems[A]. Proc GLOBECOM ’09[C]. 2009. 2799-2804.

[5] LIANG Z, CHEW Y H, KO C C. On the modeling of a non-cooperative multicell OFDMA resource allocation game with integer bit-loading[A]. Proc GLOBECOM ’09[C]. 2009. 2805-2810.

[6] NEEL J, REED J H, GILLES R P. Game models for cognitive radio algorithm analysis[A]. SDR Forum Technical Conference[C].2004.

[7] HUANG J, BERRY R, HONIG M L. Auction-based spectrum sharing[J]. Mobile Networks and Applications (MONET), 2006,11(3):405-418.

[8] CHEN L, IELLAMO S, COUPECHOUX M, et al. An auction framework for spectrum allocation with interference constraint in cognitive radio networks[A]. INFOCOM, 2010 Proceedings IEEE[C]. 2010. 1-9

[9] HUANG J W, KRISHNAMURTHY V. Truth reveling opportunistic scheduling in cognitive radio systems[A]. SPAWC '09[C]. 2009.91-95.

[10] TAN X Z, LIU Y T, XU G S. Dynamic spectrum allocation in cognitive radio: auction and equilibrium[A]. Proc International Forum on Information Technology and Applications (IFITA)[C]. 2009. 554-558.

[11] SIMEONE O, STANOJEV I. Spectrum leasing to cooperating secondary ad hoc networks[J]. Selected Areas in Communications, 2008,26(1): 203-213.

[12] HADDAD M, ELAYOUBI S E. A hybrid approach for radio resource management in heterogeneous cognitive networks[J]. Selected Areas in Communications, 2011, 29(4): 831-842.

[13] IEEE 802.22 working group on wireless regional area networks[EB/OL]. http://www.ieee802.org/22/.

[14] CORDEIRO C, CHALLAPALI K, BIRRU D, et al. IEEE 802.22: the first worldwide wireless based on cognitive radio[A]. IEEE International Symposium on New Frontiers in Dynamic Spectrum Access Networks (DySPAN'05)[C]. 2005.328-337.

[15] IEEE 802.16h: amendment 2: improved coexistence mechanisms for license-exempt operation[EB/OL]. http://standards.ieee.org/ getieee802/download/802.16h-2010.pdf.

[16] IEEE 802.11s[EB/OL]. http://www.ieee802.org/11/ Reports/tgs_ update.htm.

[17] FEDERAL C C. Establishment of Interference Temperature Metric to Quantify and Manage Interference and to Expand Available Unlicensed Operation in Certain Fixed Mobile and Satellite Frequency Bands[R]. ET Docket 03-289, Notice of Inquiry and Proposed Rulemaking, 2003.

[18] FUDENBERG D, TIROLE J. Game Theory[M]. Massachusets,USA:MIT Press, 1991.

[19] YATES R D. A framework for uplink control in cellular radio systems[J]. IEEE Journal on Selected Areas in Communications, 1995,13(7): 1341-1347.