认知MIMO MAC最优迭代注水算法

魏飞，杨震

（南京邮电大学 宽带无线通信与传感网技术教育部重点实验室，江苏 南京 210003）

1 引言

可分配频谱资源的短缺以及已分配频谱利用率偏低的差异现状已成为制约无线通信发展的瓶颈。认知无线电[1]技术通过认知无线电（CR, cognitive radio）用户或称为次用户（SU, secondary user）与主用户（PU, primary user）共享频谱资源的方式来最大化频谱利用率，作为一种解决频谱资源短缺困境的有效技术手段正受到广泛的研究。在CR场景中，CR用户通常可采用基于频谱空洞（spectrum hole）或干扰温度约束的方式与PU共享频谱资源，前者通过检测PU的活动性，当发现PU处于静默状态时（即PU不在通信）接入PU的空闲频谱，后者则是一种与PU同时共存的方式，通过使得所有CR用户对PU接收端的叠加干扰限制在PU的干扰门限内，在保证PU正常通信的前提下与PU共享频谱。

近年来，CR研究从最初的在时域与频域与PU共存拓展到空间域，主要集中在满足给定的PU干扰温度约束的条件下如何给 SU分配资源（如发送功率以及空间方向选择）以优化 CR系统的某种性能度量[2～7]。文献[2]研究了如何设计发送协方差矩阵使得单个MIMO CR用户获得的信息速率最大；文献[3]研究了单个MIMO CR用户在完全获取、部分获取以及无法获取其与 PU接收端信道状态信息时最大化信干噪声比(SINR,signal-to-interference- plus-noise ratio)的波束赋形问题；文献[4]研究了多用户CR构成的多址接入信道(MAC, multiple access channel)中最大化加权速率和的最优功率分配问题；文献[5]研究了在使用零强制的决策反馈均衡器的情况下，多用户 CR构成的SIMO MAC中的速率和最大化以及SINR平衡问题，提出了联合波束赋形和功率分配算法；文献[6]研究了在CR非完美获取其与PU接收端信道状态信息时，最大化多用户MISO CR系统中的最小SINR的强健波束赋形设计问题；文献[7]研究了多用户 CR系统构成的广播信道(BC,broadcast channel)中使得加权速率和最大的最优发送协方差矩阵设计问题。

然而，据本文作者所知，迄今为止尚未有文献研究如何设计 CR发送协方差矩阵以使得多用户CR构成的 MIMO MAC的速率和最大，即认知MIMO MAC的速率和最大化问题。虽然传统无线环境下的MIMO MAC已被充分研究，如在文献[8]中，Wei Yu等提出一种迭代注水算法用于求解MIMO MAC的速率和最大时的最优发送协方差矩阵。然而，由于缺乏对PU接收端叠加干扰的控制，已有算法无法确保满足PU干扰温度约束，因而不适用于CR系统。同时，由于文献[8]中的算法只适用于含有一个与发送协方差矩阵相关的约束条件的情况（即单用户最大发送功率约束），这使得文献[8]中的算法无法直接应用于受发送功率与干扰温度双重约束的CR系统。

本文研究了认知MIMO MAC的速率和最大化问题，其主要内容及创新处如下：本文将认知MIMO MAC速率和最大化问题表示为一个凸优化问题，通过部分对偶分解[9]松弛干扰温度约束，将原始凸优化问题分解为相互联系的2个子问题。文中提出一种迭代算法，通过交替进行对偶变量更新与顺序迭代注水运算求解分解后的子问题，从而得到使得速率和最大的SU最优发送协方差矩阵。最后通过仿真展示算法的有效性与快速收敛特性，以及PU干扰温度约束对认知MIMO MAC信道的最大速率和的影响。

2 系统模型与问题表述

2.1 系统模型

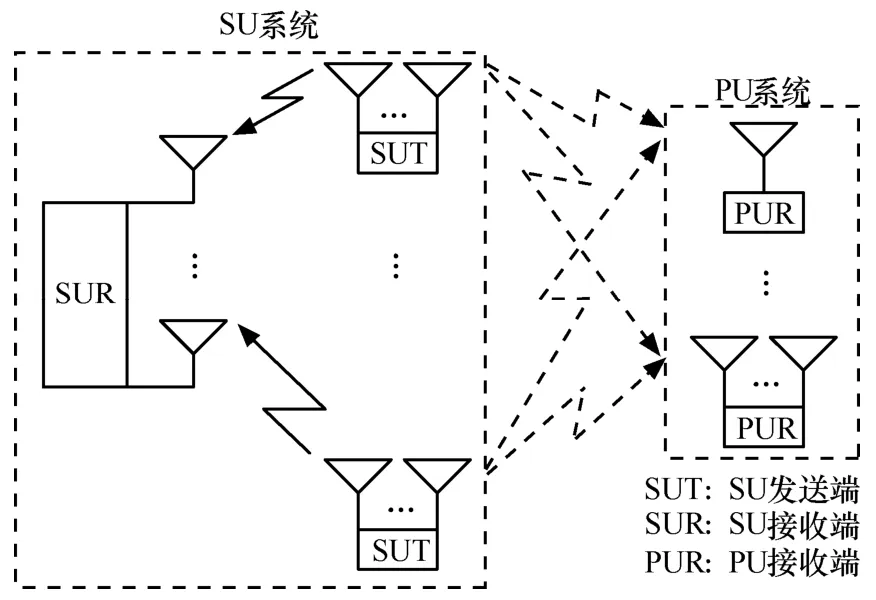
图1 SU与PU共享频谱场景图

图2所示的是上述频谱共享场景所对应的认知MIMO MAC信道模型，简单起见，图中仅示出SU发送端与第j个 PU接收端之间的信道。基于上述信道模型，SU共同接收端接收到的信号向量可表示为

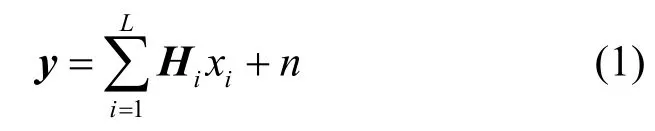
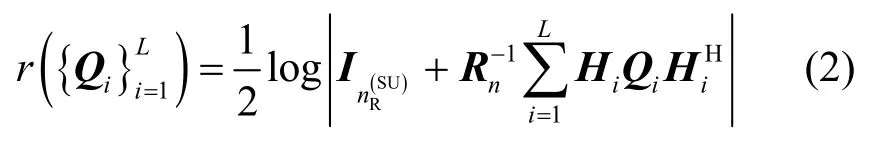
其中，SUi的发送协方差矩阵Qi被定义为Qi，Rn被定义为， E{·} 表示取均值；为阶单位矩阵。同时，SU发送信号会对PU接收端造成干扰，PU接收端j接收到的SU的干扰信号可表示为

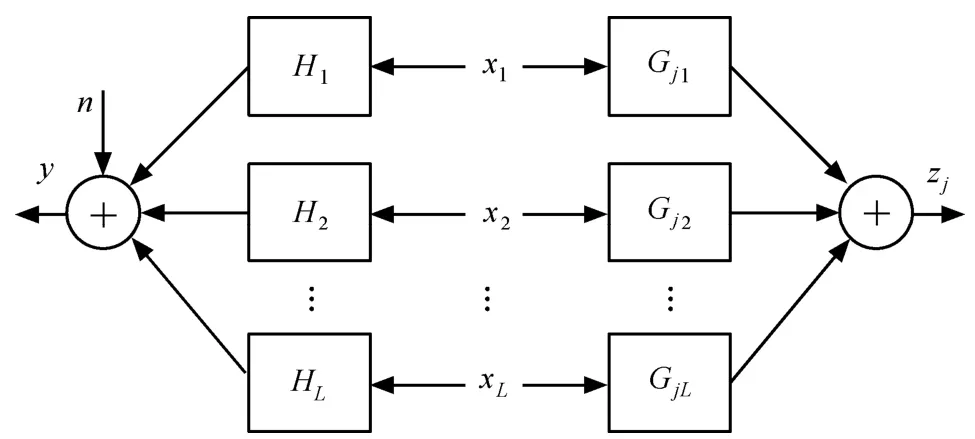
图2 认知MIMO MAC模型

2.2 问题表述

每个 SU发送信号时会受到自身发送功率约束，第i个 SU的发送协方差矩阵构成的集合Qi可表示为

在认知MIMO MAC中，为不影响PU的正常通信活动，SU在选择发送协方差矩阵时需使PU接收到的SU干扰信号的叠加功率小于一给定值，即PU干扰温度约束，如式(5)所示。

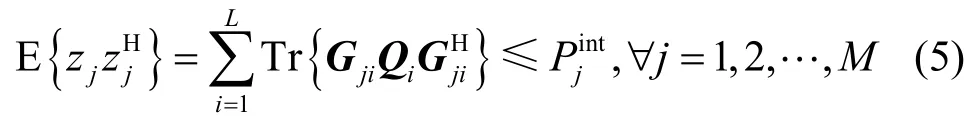
在给定发送功率约束与PU干扰温度约束下，本文研究的认知MIMO MAC速率和最大化问题可表述为

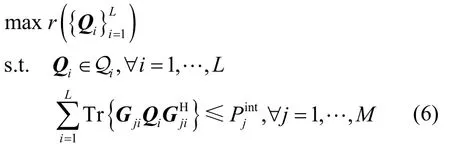
显然， r (Q1,… ,QL)为发送协方差矩阵的凹函数，上述问题为凸优化问题。如不考虑上式中的干扰温度约束，式(6)则为传统MIMO MAC速率和最大化问题，这样的问题可由多个用户按顺序依次进行迭代注水[8]来求解。然而干扰温度约束的存在使得各 SU的发送协方差矩阵互相耦合，这使得文献[8]中的算法无法通过简单地拓展应用于 CR系统。下面首先通过部分对偶分解[9]来去除干扰温度约束的影响。

3 部分对偶分解

对式(6)中的原始问题进行部分对偶分解，松弛PU干扰温度约束，可得到Lagrange函数为

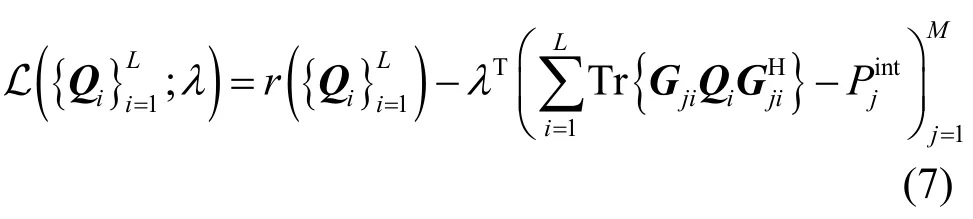
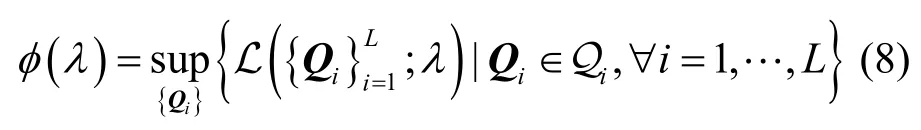
其中，sup表示上确界。

由于原始优化问题(式(6))中目标函数为凹函数，且干扰温度约束是线性不等式约束，因而强对偶性存在的条件满足，由强对偶性定理[11]，式(6)等价于Lagrange对偶问题如下

可以看出，通过以上部分对偶分解，原始优化问题被分解为2个相对简单的问题，即子问题(式(8))以及式(9)。由 φ ( λ)是关于λ的仿射函数族的点式上确界，可知 φ ( λ)是λ的凸函数，从而子问题(9)总是存在唯一的最优解。当子问题(式(9))的最优解λ*被确定后，使得子问题(式(8))中值最大的即为取得最大速率和的SU最优发送协方差矩阵，且此时。

4 算法

4.1 求解子问题(式(8))

首先，需要研究在给定任意λ值时如何求解子问题(式(8))，显然子问题(式(8))即为以下的优化问题：

观察到优化问题(式(10))类似于传统MIMO MAC速率和最大化问题[8]，不同之处在于目标函数带有一个与λ有关的附加项，因而本文使用与求解传统MIMO MAC最大速率和类似的方法：首先令Q1之外的其他{Qi}i≠1为常量，优化Q1，然后令Q2之外的其他{Qi}i≠2为常量，优化Q2，以此类推循环优化其中的单个变量，直至达到问题的全局最优解。因此，优化问题(式(10))等价于所有SU分别按顺序求解下面的凸优化问题

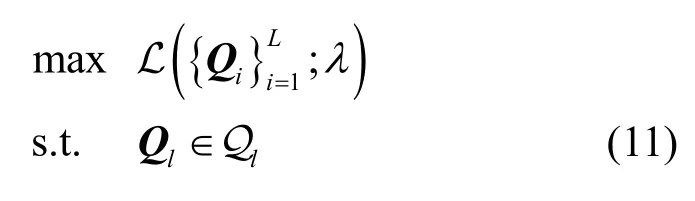
注意到式(12)中的前两项为与Ql无关的常量，所以，对任意给定的对偶变量λ，优化问题(式(11))等价于

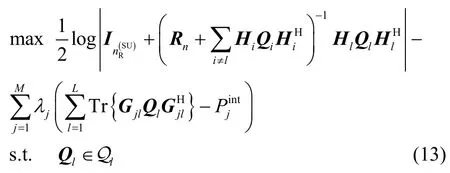
由于优化问题(式(13))是凸优化问题，因而其最优解的充分必要条件即为KKT（karush-kuhntucker）条件，给出如下：

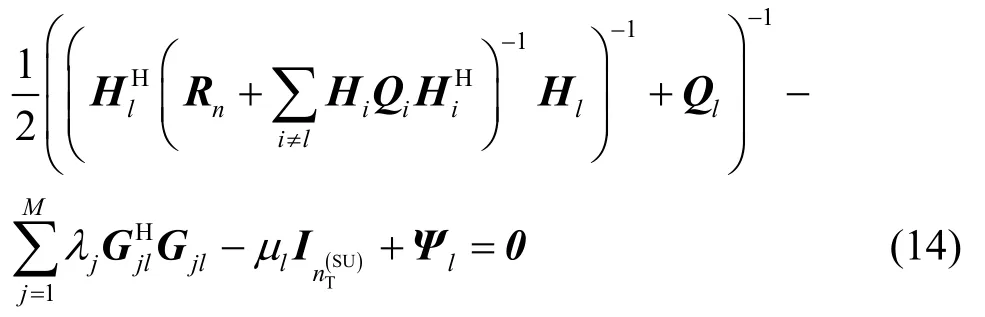
其中，lμ与Ψl分别为对应于最大发送功率约束以及正半定发送协方差矩阵约束的对偶变量。

由KKT条件可知优化问题(式(13))的最优解Ql可通过以下的注水运算求解：

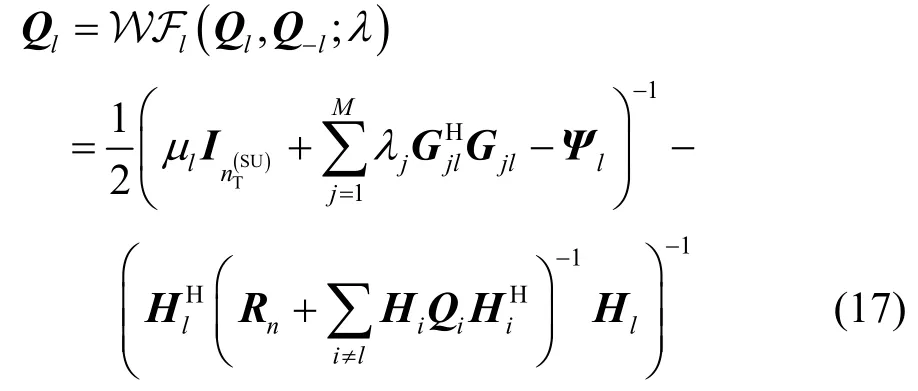
其中，μl的选择需使式Tr{Ql}≤成立，Ψl的选择需使Ql0。由于式(17)中的计算需要确定2个对偶变量μl以及Ψl，同时Ψl还是矩阵变量，这使得通过式(17)计算最优解几乎不可能。但利用Ql0等价于Ql的所有特征值非负的性质，可将式(17)等价于以下更具有实际操作意义的运算符：

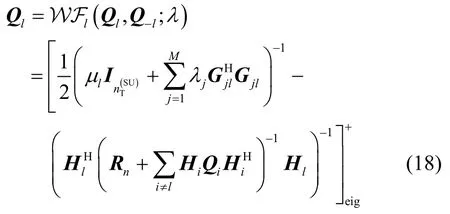
算法1所示的是求解子问题(式(8))的顺序迭代注水算法的主要步骤。由于算法1中的迭代注水总是使得子问题(式(8))中的目标函数值单调非递减，而子问题(式(8))中的目标函数具有上界且是凹的，因而算法1总是能够收敛到唯一最优解。

算法1 顺序迭代注水。

步骤1 初始化迭代指数k1=0；

步骤2 所有SU按下式更新发送协方差矩阵

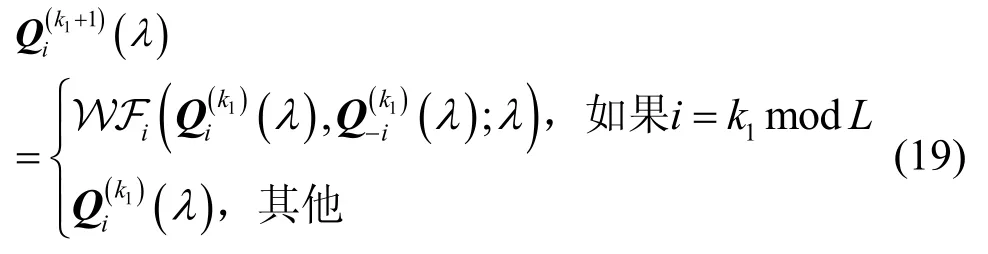
其中，式(19)中的注水运算WF(·)见式(18)，mod表示模运算；

步骤3 若满足停止条件，k1←k1+1停止并输出

步骤4 设置，返回步骤2。

4.2 求解子问题(式(9))

由于子问题(式(9))中的目标函数φ( )λ是不可微的，这使得一些基于梯度的方法（如最速下降法、牛顿法）无法应用于求解φ( )λ的极值，因而本文使用基于次梯度的方法。首先需要确定函数φ( )λ的次梯度，对于函数φ( )λ的次梯度，有如下命题成立

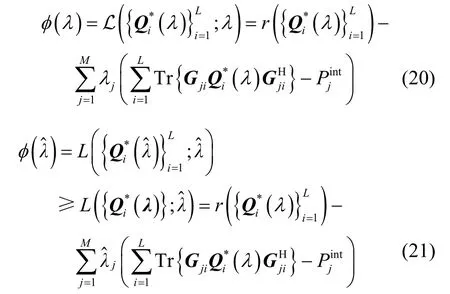
由式(21)减去式(20)易知：

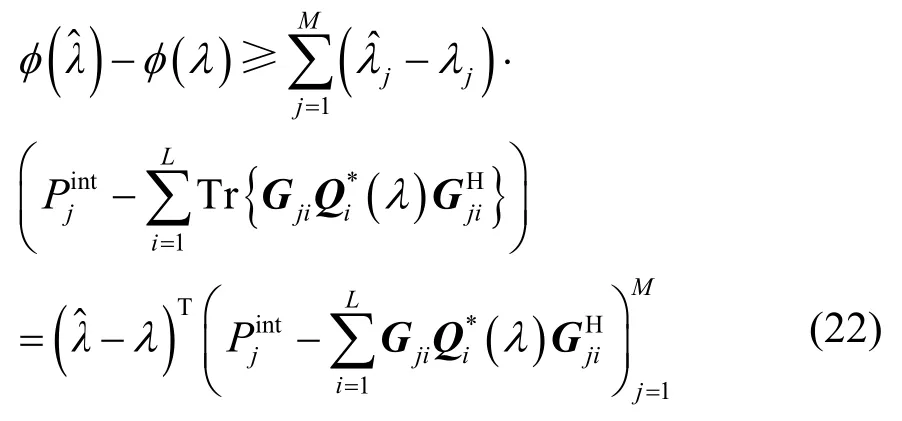
而对于凸函数φ( )λ，向量d为其在λ点处的次梯度[11]，如d满足以下的不等式：

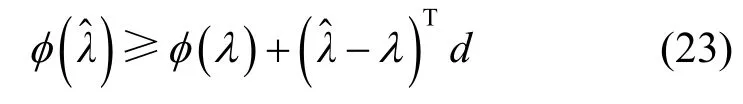
最后，比较式(22)和式(23)易知命题成立。

证毕。

算法2中所示的是基于次梯度投影法[12（]projected subgradient method）的对偶变量λ更新算法的主要步骤。文献[12]中证明了次梯度投影法能够收敛到最优解，由于φ( λ)是凸函数，因而算法2总是能够收敛到唯一最优对偶变量。当最优对偶变量λ*被取得后，其相应的(λ*)，i=1,2,…,K即为所求的SU最优发送协方差矩阵。

算法2 对偶变量更新。

步骤1 选择任意λ(0)≥0，(λ(0))∈Qi，i=1,…,L，初始化迭代指数k2=0；

步骤3 按下式更新对偶变量。

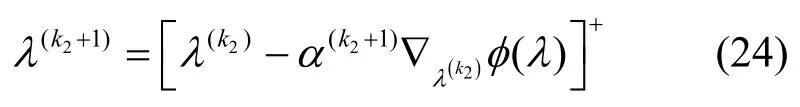
其中，α(k2+1)为第k2+1次迭代的步长；

步骤5 设置k2←k2+1，返回步骤2。

5 仿真结果

本节通过MATLAB数值仿真展示本文算法的有效性。仿真中使用的认知无线场景包含有4个2天线SU发送端与一个2天线SU公共接收端以及1个单天线PU接收端。简单起见，设置各个SU发送端与SU接收端的距离相等为dss，各个SU发送端与PU接收端的距离相等为dps。仿真中所使用的随机信道系数为0均值单位方差循环对称复高斯的，如表1所示；SU共同接收端的复高斯噪声向量n是0均值、方差的，简单起见，归一化=1，设置SU的发送功率相等为P；路径损耗系数设置为γ注1注1 经过路径损耗后的信道系数可表示为Hi=，Gji=， ∀i=1,2,…,L ，j=1,2,…,M 。注2 设定干扰门限为2倍与4倍。初始化算法参数λ(0)=0，(0)=0。

图3中所示的是在表1中的信道系数下经典算法与本文算法取得的速率和以及对PU的叠加干扰随迭代次数的变化过程，干扰门限分别设置为Pint=2与Pint=4注2注1 经过路径损耗后的信道系数可表示为Hi=，Gji=， ∀i=1,2,…,L ，j=1,2,…,M 。注2 设定干扰门限为2倍与4倍。从图中可以看出，相对于经典算法，本文算法能够很好地控制SU对PU的叠加干扰，满足PU的干扰温度约束，同时，由于要满足PU干扰温度约束，本文算法收敛到最优解所需的迭代次数有所增加，但仍然具有较快的收敛速度。

表1 信道系数

表2 最优发送协方差矩阵（ P/=10dB，dss=1，dps=2，γ=2.5）

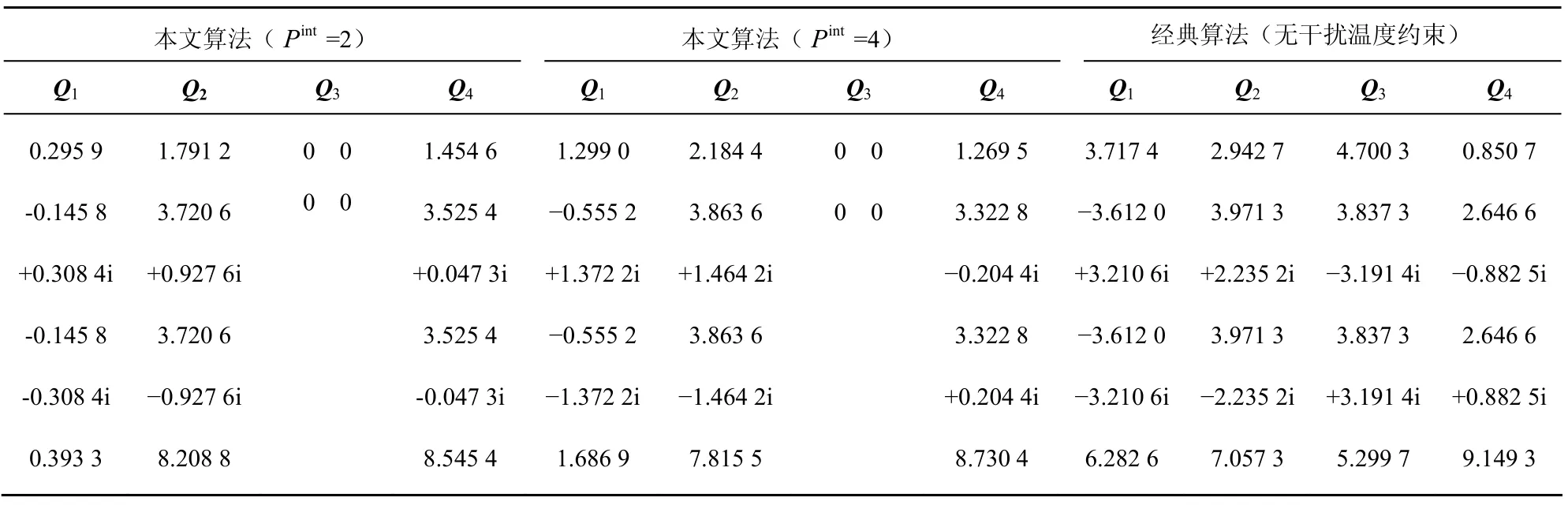
表2 最优发送协方差矩阵（ P/=10dB，dss=1，dps=2，γ=2.5）

?

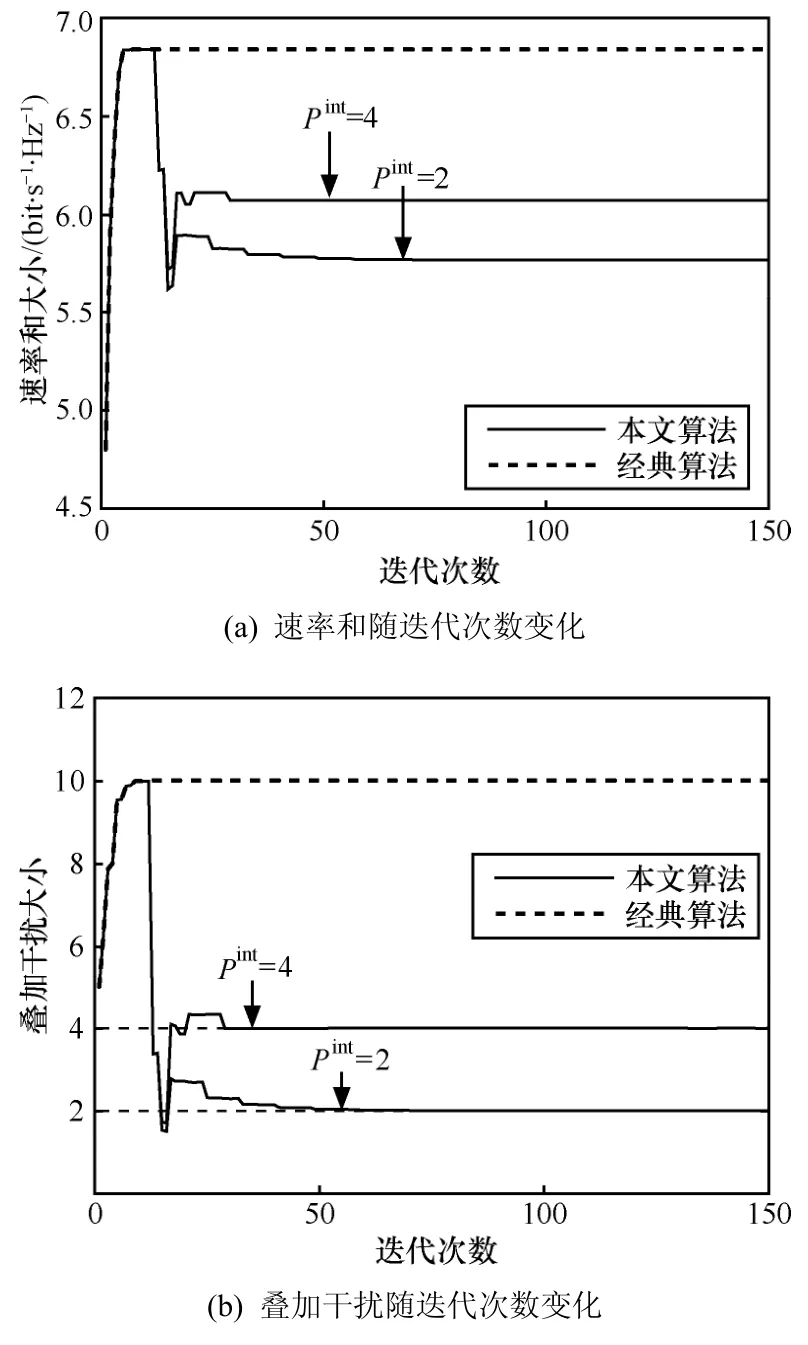
图2 算法收敛过程（ P/=10dB，dss=1，dps=2，γ=2.5）

表2所示是上面的仿真中最后得到的SU最优发送协方差矩阵。注意到相对于无干扰温度约束时，在 Pint为2以及4时，SU3的最优发送协方差矩阵Q3=0。对任一SU来说，理想的信道状况指的是它到SU接收端之间的信道传输特性好而到PU接收端间的信道传输特性差。SU3的信道状况差于其他 3个SU，因而相对于其他SU，SU3在对PU产生单位干扰时能够给CR系统提供的信息速率是最小的，因而从系统速率和最大的角度出发，只有在其他 3个 PU都已满功率传输且叠加干扰仍小于干扰门限时才会考虑SU3，而由表2中可知，Q1的主对角元素之和小于发送功率10，SU1尚未满功率传输而此时叠加干扰就已达到干扰门限，因而SU3选择不发送任何信号。同时从表中可以看出，随着intP 的上升，SU1能够使用的发送功率也在增大。

图4中所示是给定不同的PU干扰门限时，认知MIMO MAC的最大速率和随SU收发端的距离的变化曲线图，同样使用了表1中信道系数。从图中可以看出，随着干扰门限intP 的不断增大，认知MIMO MAC的速率和不断逼近没有干扰门限限制的传统MIMO MAC的最大速率和。在干扰门限增大至Pint=12时，由于此时PU干扰温度约束失效（由图3(b)中经典算法对PU产生的叠加干扰小于 Pint=12可知），从而认知MIMO MAC与传统MIMO MAC的最大速率和相等。

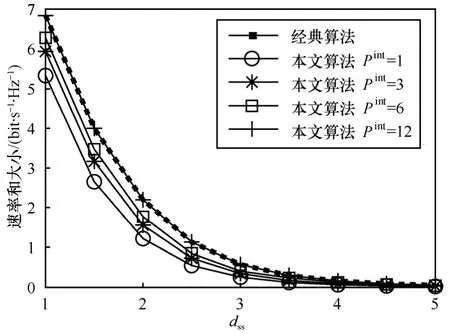
图4 不同干扰门限下的速率和vs.dss（ P/=10dB，dps=2，γ=2.5）

6 结束语

本文研究了发送功率以及干扰温度约束下的认知MIMO MAC的速率和最大化问题,提出了一种迭代注水算法求解使得速率和最大的SU最优发送协方差矩阵。仿真结果表明本文算法具有快速收敛的特点且很好地满足了干扰温度约束，能够适用于认知无线电环境。

[1] HAYKIN S. Cognitive radio: brain-empowered wireless communications [J]. IEEE Journals on Selected Areas in Communications, 2005,23 (2): 201-220.

[2] ZHANG R, LIANG Y C. Exploiting multi-antennas for opportunistic spectrum sharing in cognitive radio networks[J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2 (1): 88-102.

[3] ZHANG Y J, SO A M. Optimal spectrum sharing in MIMO cognitive radio networks via semidefinite programming[J]. IEEE Journal on Selected Areas in Communications, 2011, 29 (2): 362-373.

[4] ZHANG L, XIN Y, LIANG Y C. Optimal power allocation for multiple access channels in cognitive radio networks[A]. Proceedings of IEEE Vehicular Technology Conference[C]. Singapore, 2008. 1549- 1553.

[5] ZHANG L, LIANG Y C, XIN Y. Joint beamforming and power allocation for multiple access channels in cognitive radio networks[J]. IEEE Journal on Selected Areas in Communications, 2008, 26 (1): 38-51.

[6] ZHENG G, WONG K K, OTTERSTEN B. Robust cognitive beamforming with bounded channel uncertainties[J]. IEEE Transactions on Signal Processing, 2009, 57(12): 4871-4881.

[7] ZHANG L, XIN Y, LIANG Y C. Weighted sum rate optimization for cognitive radio MIMO broadcast channels[J]. IEEE Transactions on Wireless Communications, 2009, 8(6): 2950-2959.

[8] YU W, RHEE W, BOYD S, et al. Iterative water-filling for Gaussian vector multiple-access channels[J]. IEEE Transactions on Information Theory, 2004, 50(1): 145-152.

[9] PALOMAR D P, CHIANG M. A tutorial on decomposition methods for network utility maximization[J]. IEEE Journal on Selected Areas in Communications, 2006, 24 (8): 1439-1451.

[10] GOLDSMITH A, JAFAR S A, JINDAL N, et al. Capacity limits of MIMO channels[J]. IEEE Journal on Selected Areas in Communications, 2003, 21(5): 684-702.

[11] BERTSEKAS D. Nonlinear Programming[M]. Belmont, MA:AthenaScientific, 1999.

[12] BOYD S, XIAO L, MUTAPCIC A. Subgradient methods[EB/OL].http://mit.edu/6.976/ www/notes/subgrad_method.pdf, 2003.