面向统计QoS保障的多时间尺度接纳控制算法

陈艳平，王慧强，冯光升，高玉龙

(1. 哈尔滨工程大学 计算机科学与技术学院，黑龙江 哈尔滨 150001；2. 哈尔滨工业大学 通信技术研究所，黑龙江 哈尔滨 150080)

1 引言

接纳控制是保障业务流QoS的有效方法之一，目前主要有2种方法，一种是基于测量的接纳控制，一种是基于参数的接纳控制。其中基于参数的接纳控制采用相关模型来预测和计算流的行为特征和估算流量，由于设定了流模型，使用的算法简单，但基于参数接纳控制算法的控制能力取决于对访问模式研究的深度以及数学模型的拟合程度。

各种新兴网络访问方式的出现导致网络数据流突发性的变化更加随机，这种随机性一方面使得构建统一、准确的业务流模型更加困难，同时也给保障业务流服务质量带来挑战。在业务流建模方面，随着音频、视频数据的增加，网络数据流不再满足泊松过程，而是表现出自相似、多分形等特性，自相似的本质是一种单分形结构，大量研究表明业务流在大时间尺度上表现出单分形，而在小时间尺度上表现出多分形特性[1]，即业务流具有特征尺度。目前业务流建模主要针对某个特征进行建模，文献[2]提出了采用分形布朗运动(FBM, fractional Brownian motion)模型描述自相似过程，但是对于非高斯(即重尾性)的自相似流突发性刻画能力有限，文献[3]提出了基于线性分形α稳定自相似过程流模型，引入了倾斜参数用于表示重尾性。文献[4]研究表明，vBNS在突发水平高的业务流用多分形流模型表示比较准确，而突发水平低的业务流并不适合用多分形流模型建模。文献[5]也表明业务流的到达快慢影响它的特性。针对多分形流，文献[6]提出了乘法多分形模型(multiplicative multifractal model)对业务流的多分形特性建模，文献[7]提出了基于小波的多分形模型描述业务流的多分形。针对流的不同特征尺度，目前还没有一个统一的业务流模型，采用单一的特征模型影响后续的业务流性能分析及QoS保障，特别是于业务流的突发性对网络性能影响很大[8]。

对业务流模型的研究可以看出，目前还没有统一模型针对流的所有特征进行建模，因此基于参数的接纳控制大多采用针对单一特征的流模型，这大大影响接纳决策的准确性。另外，在QoS保障方面，大多采用确定服务质量参数[9]，然而越来越多的音频、视频等数据对延迟等性能具有一定的容忍能力，统计QoS保障成为接纳控制新的研究方向。其中统计网络演算是新兴的QoS统计分析的理论，以该理论为基础研究基于参数的接纳控制方法方兴未艾。文献[10，11]提出了基于网络演算的统计QoS保障接纳控制方法，但两者都基于一个前提，即业务流符合线性包络，该方法不能用于自相似、多分形业务流的接纳分析。

针对以上研究问题，本文提出通过在线测量，估计业务流的突发水平，进而采用不同的模型对网络业务流进行建模；基于选定的流模型有效带宽推导其有效包络，采用统计网络演算对业务流进行性能分析，根据获得的性能参数进行接纳控制决策，以此保障业务流的统计QoS。内容组织如下：第2节给出用于统计QoS分析的网络演算基本定义及定理；第3节介绍本文接纳控制的系统模型；第4节给出自相似、多分形流模型估计方法、有效包络获得方法及突发期的估计，结合第2节的相关理论给出接纳控制算法；第5节仿真实验从统计QoS保障、带宽利用率方面对算法的性能进行验证；第6节是结束语。

2 统计QoS分析基础

统计网络演算为网络性能分析提供了新的研究方法，为实现统计QoS保障提供了新理论，为接纳控制等技术提供基础。本节简要介绍下文用到的统计网络演算基本理论和表示符号。业务流的到达过程和离开过程表示为A=(A( t))t≥0和D=(D( t))t≥0，其中，A( t)、D( t)分别表示业务流在t时刻到达和离开网络节点的累积业务量。很明显，A, D都是非降左连续的，并且∀t≥0,D( t)≤A( t)。

定义1 (非负广义递增函数集)[12]：F={f(·):∀0≤x≤y, f( x)≥0,f( x)≤f( y)}

定义2 (非负广义递减函数集)[12]：={f(·):∀0≤x≤y, f( x)≥0,f( y)≤f( x)}

定义3 (统计到达曲线)[12]：给定函数α∈F,εA∈，如果业务流的到达过程A满足P{ A( s, t)-G( t-s)＞x}≤εA(x)，其中，A( s, t)=A( t)-A( s),0≤s≤t, x≥0，则称业务流A具有误差函数为εA的统计到达包络G。

定义4 (统计服务曲线)[12]：给定函数β∈F,εS∈，到达网络节点的业务流，其到达过程为A，如果该业务流的离开过程满足P( D( t)＜A⊗[β-x]+(t +τ0))≤εS(x)，其中，f( u)du＜∞，则称该网络节点为业务流A提供了误差为εS的统计服务曲线β。

统计网络演算利用到达曲线和服务曲线推导出网络输出、延迟、积压等性能指标，这其中用到2类重要的运算，即最小加卷积和最小加去卷积，卷积定义见定义5，有关去卷积及统计网络演算其他理论详见文献[12]。

定义5 (最小加卷积)[12]：f, gF∀ ∈ ，函数f, g的最小加卷积运算为其中，t≥0。

定义6 (统计延迟)[12]：∀t≥0，统计延迟W( t)定义为

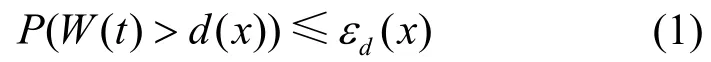
其中延迟上界为

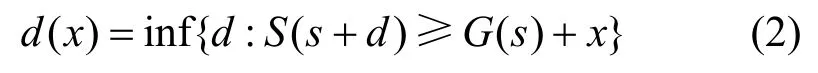
目前网络演算理论本身还不完善，用于性能分析的流模型主要有3种[12]，文献[13]将有效带宽与网络演算中的统计包络进行融合，从而扩宽了网络演算的应用范围。下面介绍有效带宽的定义及有效带宽和有效包络转换定理。

定理1[13]到达过程A( t)的有效带宽为α(s, t)，其有效包络为

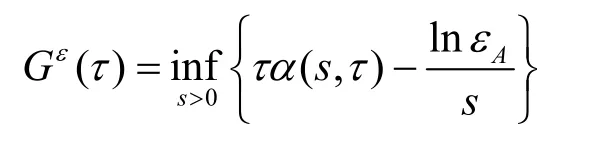
其中，εA为业务流到达曲线的误差函数，s为空间参数，表示业务流的到达分布特征，t为时间参数，表示时间间隔长度。

3 系统模型

为了突出本文提出的思想及说明问题的便利性，仅考虑单个节点的接纳控制，系统模型如图1所示。在该模型中，业务流是一组具有相同包头属性的包列，当数据分组到达时，流模型估计模块首先分析流的突发水平，通过在线测量决定其流模型，在线测量过程并不在业务流的接纳控制中，因此减少接纳控制本身对业务流性能的影响。流模型采用定义3表示，根据流模型推导流的有效包络及突发期。参数估计模块估计服务节点当前剩余的服务能力，采用定义4的服务曲线表示。接纳控制算法模块首先根据流的有效包络和当前节点的剩余服务能力利用网络演算理论推导流的统计延迟，基于统计延迟及突发期来进行接纳决策。

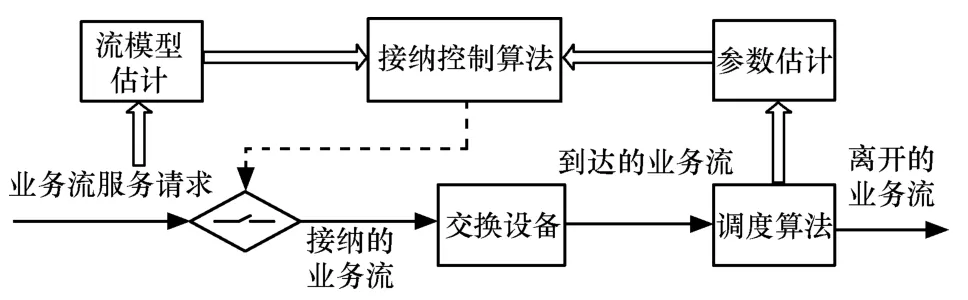
图1 系统模型

对于业务流的QoS要求，本文主要考量延迟参数，统计延迟采用定义6表示，其通过业务流模型和网络节点的服务能力推导而来，而节点动态提供的服务能力也与当前网络节点中的业务流有关，因此，业务流模型的选择将在很大程度上影响接纳控制的性能。本文根据不同业务流在不同时间尺度上表现出不同的特性，进而采用不同的业务流模型，以提高接纳控制的性能，并采用网络演算理论对流进行性能分析，实现统计QoS保障。

4 多时间尺度接纳控制算法

根据文献[1,14]，业务流在小的时间尺度上表现出多分形特性，而在大的时间尺度上表现出自相似性。然而目前的业务流建模大多数是对流的自相似性和多分形分别建模，没有统一的模型描述多特征尺度的业务流。研究表明在突发水平较高时采用自相似模型刻画流较准确，而在突发性较低时采用多分形流建模较准确，因此如果接纳控制算法仅采用一种流模型，对接纳控制的性能产生很大的影响，例如，假设网络业务流目前的突发水平较低，如果采用自相似模型，使得对业务流的估计过高，如果业务流的突发水平较高而采用多分形流模型，则对的业务流实际业务量估计不够。本文提出多尺度接纳控制算法，通过预测网络业务流采用哪种模型建模更加准确，进而决定选择相应的流模型用于接纳控制。另外，由于在流的突发期网络性能波动较大，为了保障业务流的统计QoS，并不是所有的流在所有的时间都需要接纳控制，本文提出在突发期推导业务流的性能，并据此对业务流进行接纳控制。

4.1 流模型估计

考虑2类流模型：自相似流和多分形流模型。首先给出，多分形和自相似的定义。

定义7(多分形)：如果一个随机过程X( t)满足以下条件，则称该过程为多分形：

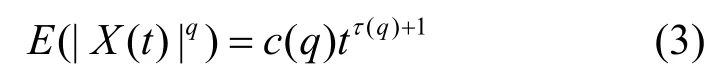
t表示时间，q表示q阶距。其中，c( q)和τ(q)分别表示多分形过程的尺度参数和距参数。如果τ(q)与q呈线性关系，则该过程为单分形，否则，呈多分形。

定义8(自相似)：如果连续过程Y( t)满足以下条件，则称该过程为自相似：

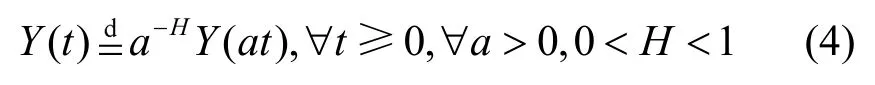
根据以上定义及文献[15]的分析，对于网络流非负时间序列X=X( t1),…,X( tN)，采用式(5)估计X的q阶距μ(m)(q)：

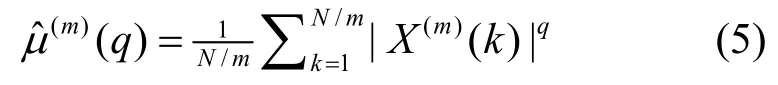
4.2 有效带宽和包络估计

网络演算是QoS分析的新兴理论，理论本身还不完善，可用于QoS分析的流模型有限，特别是统计QoS分析。有效带宽是另外一个重要的性能分析工具，更多类型的流都可以获得其有效带宽。文献[13]提出了有效带宽和有效包络的转换定理，根据此定理，更多类型的流可用于网络演算的统计QoS分析，进而保障业务流的统计QoS。对于分形流模型和自相似流模型，本文分别采用 AWMM (adaptive wavelet-based multifractal model)和FBM (fractional Brownian motion)，并根据定理1给出2类模型对应的有效包络，获得这2类流模型的有效包络就可以利用网络演算推导流的延迟等性能参数，为接纳控制提供决策基础。

根据文献[7]提出的分形流模型 AWMM，其到达过程X( k)的有效带宽为

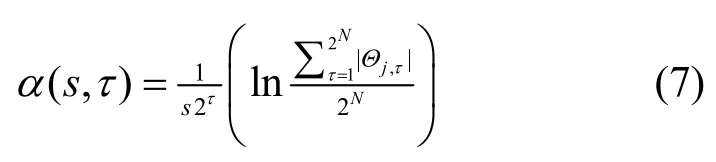
自相似过程采用FBM流模型，其有效带宽为[16]

其中，ρ表示流的平均速率，β表示标准差，H表示hurst参数。

根据定理1，分形流的有效包络为

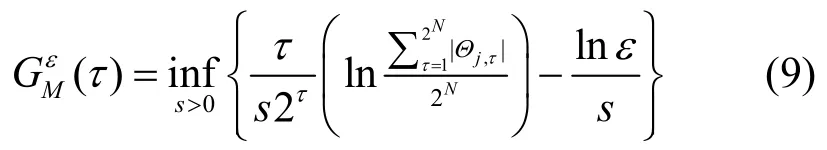
自相似流的有效包络为

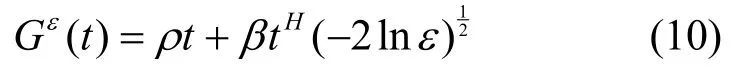
推导过程极为简单，这里不赘述。

4.3 突发时间估计

引理1[13]假设服务节点的服务速率为常数C,调度算法为 workconserving，如果聚集流的到达过程Ac满足

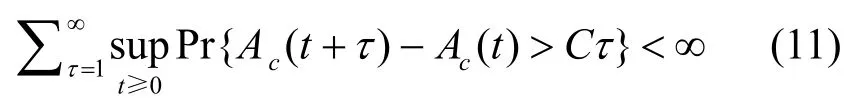
对于给定的 ε ∈ ( 0,1)，T为突发时间的上界，选择最大T使得：

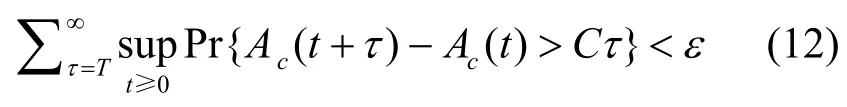
根据引理 1，为了获得突发期上界，首先要验证流模型是否符合引理的假设条件。根据切比诺夫不等式(Chernoff bound)，有

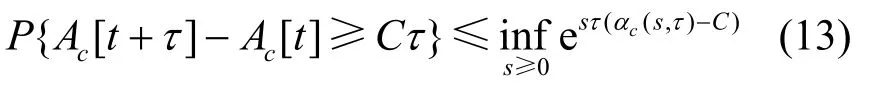
对于多分析流模型，将有效带宽式(7)代入式(13)，则式(13)的右侧为设，根据阿贝尔定理有

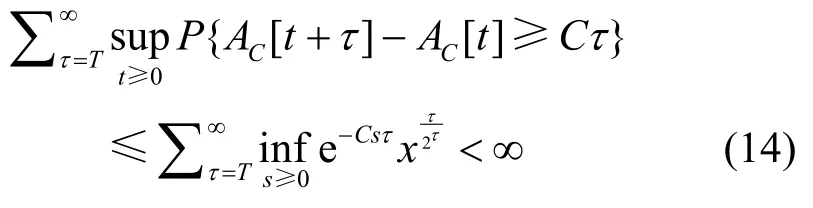
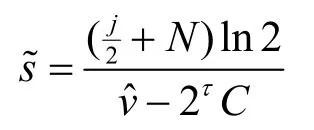
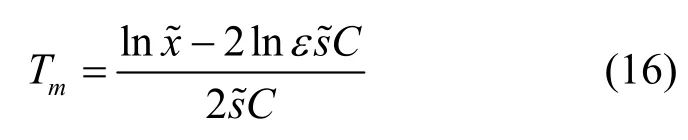
同理,FBM流的突发期为

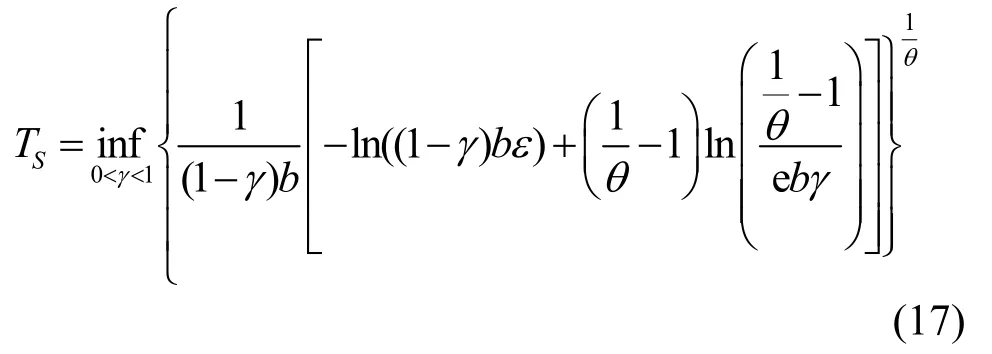
4.4 接纳控制算法

算法思路：一个新流向网络节点请求服务，延迟要求满足式(1)，为实现流的统计QoS要求，算法采用统计网络演算对流进行性能分析，基于分析结果进行接纳控制。由于流在不同时间尺度上表现出不同特性，因而有不同的流模型，本文考虑自相似和多分形2类主要流模型，算法首先通过在线测量，选取适当的时间尺度t，判断流的突发水平，据此选定流模型。根据网络数据量变化的统计结果，即数据量发生突发性变化是与特定时间段相关的，因此，在这样的时间段内能够反映业务流特征的最短时间作为时间尺度t；另外，多分形流模型还不能直接用于统计网络演算分析，算法通过有效带宽和有效包络转换定理，获得多分形流模型的有效包络，使得多分形流模型能够用于统计网络演算分析；由于接纳算法本身会对流的性能产生影响，因此接纳决策时机的选择对满足流的性能也至关重要，算法通过推导估计流的突发期，在流的突发期内对流进行接纳控制。

算法具体描述如下：

1) 初始参数设置。设节点的服务速率为C，到达曲线、服务曲线和延迟的误差参数分别设为εa,εs, εd；

2) 选取时间尺度t，根据式(5)和式(6)判断当前流的突发水平，确定流模型。若采用自相似流模型，转入3)，若采用多分形模型，转入4)；

3) 计算流的均值和方差，根据式(8)得到流的有效带宽，根据式(10)计算流的有效包络，根据式(17)得到流的突发期上界；

5) 在突发期内，一个新流到达，根据式(2)推导延迟界，如果满足流的延迟要求则接纳，否则丢弃。对于非突发期内的流则全部接纳。

该算法以业务流QoS参数作为接纳决策的依据，只有满足业务流QoS参数要求的流才被接纳，通过这样的方式来实现对业务流QoS保障。

5 仿真实验

采用2个数据集对算法的性能进行验证，分别是LBL-TCP-3和pAug。研究表明，LBL-TCP-3具有多分形属性，而pAug具有自相似性[1]，AWMM流模型较适合前者数据的建模，而FBM模型较适合后者。首先，考察针对相同的数据采用AWMM和FBM流模型对接纳性能的影响。

LBL-TCP-3和pAug数据流的统计参数如表1所示。采用单个服务节点，服务模式为workconserving，网络节点带宽为1Mbit/s。

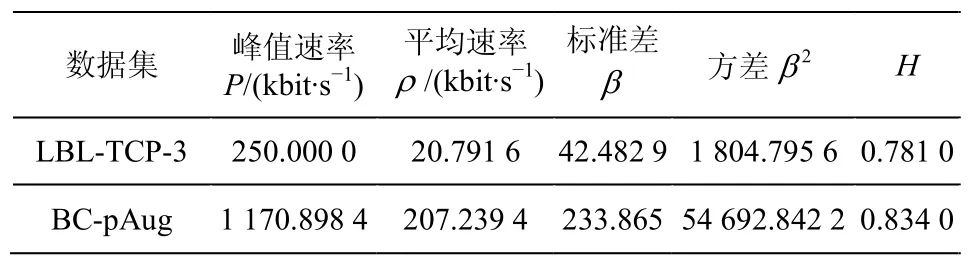
表1 数据流的统计参数

首先，针对LBL-TCP-3数据，分别采用2种模型进行建模，获得的有效包络如图2所示。从图2中可以看出，采用FBM模型推得的有效包络要高于多分形流模型的有效包络，这一结果将直接增加向服务节点申请的带宽，如果数据流的突发水平并没有这么高，将导致资源的浪费，资源利用水平低。图3给出了LBL-TCP-3数据流在满足统计延迟要求的情况下接纳流的数量，从图中可以看出，对比AWMM模型，FBM流接纳的流数较少。而对于pAug突发水平较高的数据流，采用FBM流模型和多分形流模型进行接纳的对比如图4所示，pAug适合采用FBM流进行建模，采用多分形流建模，由于计算所需的有效带宽较小，过多的接纳了数据流，致使产生拥塞，使得很多分组丢弃，导致带宽利用率下降，且业务流的延迟加大。采用本文算法通过在线测量，能够识别出流的类型因而解决流模型对接纳性能的影响。

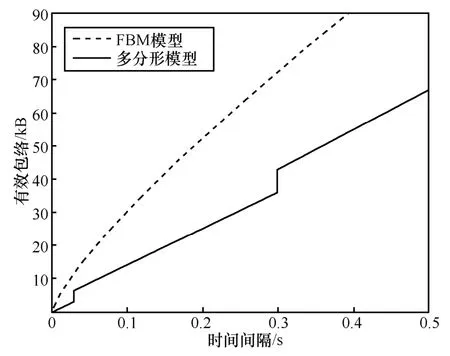
图2 流的有效包络

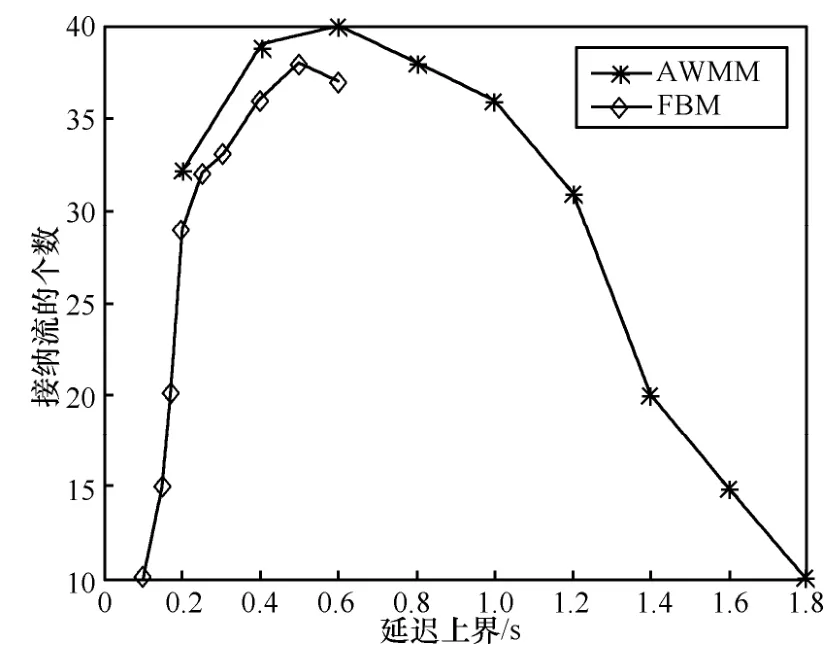
图3 AWMM和FBM流模型接纳数对比(LBL-TCP-3)

图4 AWMM和FBM流模型接纳数对比(pAug)

其次，针对LBL-TCP-3数据流，考察2种情况：

方法 1 判断流的突发期，只有在流的突发期内进行流的接纳决策；

方法2 只要新的数据流到达就进行接纳决策。

图5给出了二者的对比。从图中可以看出，在流的突发水平较低，在非接纳控制情况下，大部分流的延迟要求能够满足，然而如果进行接纳控制，尽管流的统计延迟要求仍能够满足，但流经历的延迟增加了。

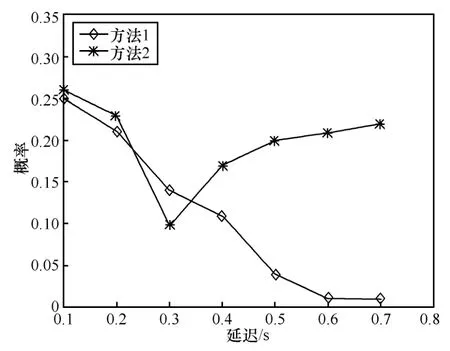
图5 流的延迟分布(LBL-TCP-3)

综上所述，针对不同的特征尺度选择不同的业务流模型使得对流模型的描述更加准确，为后续准确的接纳控制提供了基础；另外，接纳控制的目的是保障或提高服务质量，但不是控制越多越能提高性能，因此控制时间的选择对业务流QoS保障也至关重要。

6 结束语

由于数据模型对实际业务流的拟合程度存在误差，特别是当前对流的自相似、多分形等特性还没有统一的数学模型，而业务流呈现多样性，目前采用一种模型对流建模的误差较大，本文通过在线测量业务流的突发水平，选取对应的业务流模型，实现了对业务流更加准确的建模，减小流建模中的误差，为后续的接纳控制提供更可靠基础。另外，由于音频、视频等数据逐渐成为网络中的主要数据形式，这类数据对服务质量有一定的容忍能力，因此QoS保障由确定性转向统计性，统计网络演算作为统计QoS分析理论，本身需要完善，在具体应用中需要结合相关理论拓展理论的应用范围，本文通过有效带宽和有效包络的转换定理，实现了多分形模型用于网络演算统计QoS分析；最后，通过接纳时机的选择尽量减小接纳控制本身对业务流性能的影响。

[1] ABRY P, BARANIUK R, FLANDRIN P, et al. Multiscale nature of network traffic[J]. IEEE Signal Processing Magazine, 2002, 19(3):28-46.

[2] NORROS I. On the use of fractional brownian motion in the theory of connectionless networks[J]. IEEE Journal on Selected Areas in Communications, 1995, 13(6):953-962.

[3] KARASARIDIS A, HATZINAKOS D. Network heavy traffic modeling using α-stable self-similar processes[J]. IEEE Transactions on Communications, 2001, 49(7):1203-1214.

[4] GAO J, RITKE R. Long-range-dependence and multifractal modeling of vBNS traffic[A]. Proceedings of the 2001 Applied Telecommunications Symposium[C]. Seattle, Washington, 2001.167-173.

[5] MAULIK K, RESNICK S. The self-similar and multifractal nature of a network traffic model[J]. Stochastic Models, 2003, 19(4):549-577.

[6] GAO J, RUBIN I. Multiplicative multifractal modeling of longrange-dependent traffic in computer communications networks[J].Nonlinear Analysis, Theory, Methods and Applications, 2001, 47(9):5765-5774.

[7] VIEIRA F H T, LEE L L. Adaptive wavelet-based multifractal model applied to the effective bandwidth estimation of network traffic flows[J]. IET Communications, 2009, 3(6): 906-919.

[8] ERRAMILLI A, NARAYAN O, NEIDHARDT A, et al. Performance impacts of multi-scaling in wide area TCP/IP traffic[A]. IEEE INFOCOM[C]. Tel Aviv, Israel, 2000.352-359.

[9] MENTH M, LEHREIDER F, BRISCOE B, et al. A survey of PCN-based admission control and flow termination[J]. IEEE Communications Surveys & Tutorials, 2010, 12(3):357-375.

[10] PAOLO G, GABRIELLA S. Resource allocation and admission control for the provisioning of quality of service in networks of static priority schedulers[J]. Computer Networks,2009, 53(2):231-243.

[11] WANG S Q, XUAN D, BETTATI B, et al. Toward statistical QoS guarantees in a differentiated services network[J]. TeleCommunication,2010,43(3-4):253-263.

[12] JIANG Y. A basic stochastic network calculus[A] ACM SIGCOMM Conference on Network Architectures and Protocols[C]. Pisa, Italy,2006.123-134.

[13] CHENG Z L, BURCHARD A, LIEBEHERR J. A network calculus with effective bandwidth[J]. IEEE/ACM Transactions on Networking,2007, 15(6):1442-1453.

[14] GONG W B, LIU Y, MISRA V, et al. Self-similarity and long range dependence on the internet:a second look at the evidence, origins and implications[J]. Computer Networks, 2005, 48(3):377-399.

[15] TAQQU M S, TEVEROVSKY V, WILLINGER W. Is network traffic self-similar or multifractal[J]. Fractals, 1997, 5(1):63-73.

[16] KELLY F. Notes on Effective Bandwidths[M]. USA: Oxford University Press, 1996.