剪力墙抗震能力设计措施有效性的校验与改进

韩 军,李英民,陈伟贤

(1.重庆大学 a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆400045;2.中山大学基建处,广州510275)

目前大部分国家抗震规范采用的抗震设计思路是取用比设防烈度水准明显偏低的地震作用(小震)进行结构构件截面设计,利用不显著降低构件承载力前提下结构足够的延性来达到在较强地震作用下结构损伤不严重,在预估的更强地震作用下(大震)不造成危及生命的严重破坏或结构倒塌的目标[1-2]。选用较低承载力的设计思路导致结构抗震的关键因素是如何保证抗侧力结构和构件的延性。20世纪70年代后期,新西兰知名学者 T.Paulay和R.Park提出的能力设计法是保证结构具有足够延性的主要技术措施,得到了一致的认可,其核心思想实际上是通过一定的构件承载能力级差设计措施来控制结构在强震下出现预期的延性破坏模式。但中国抗震规范[3]采取的钢筋混凝土结构能力设计措施在汶川地震中并未有效引导结构形成预期的破坏模式[4-5],规范采取的抗震能力设计措施的有效性引起了广泛关注,开展了有针对性的研究,但大多集中在框架结构的能力措施上[6-8];汶川地震中少量剪力墙结构震害表明,按中国2001版抗震规范设计的剪力墙结构抗震性能基本达到预期设防目标要求,但重灾区剪力墙结构和框剪结构较少,未能充分检验剪力墙结构抗震设计能力措施控制其出现预期破坏模式的有效性和合理性,且中国抗震规范采取的剪力墙能力设计措施明显有别于其他国家规范,中国2010版抗震规范修订时对能力设计措施进行了修改,但对其有效性进行计算分析和试验验证的研究很少见,已有研究多侧重于“强墙弱连梁”和框架剪力墙的多道防线[9-11],针对剪力墙自身抗弯和抗剪的能力设计措施的研究很少,其他国家有少数文献[12-13]对规范采用的剪力墙能力设计措施进行了校验,但由于各国规范之间存在的显著差别,其结论并不适用于中国规范。因此,亟需对中国剪力墙能力设计措施的有效性进行校验和评估,找出其中存在的问题并进行改进,以便剪力墙构件在强震中更为有效的实现其预期破坏模式,保证其在大震甚至是超大震下的抗倒塌性能。该文通过理论分析指出中国01版抗震规范中剪力墙能力设计措施可能存在的问题;对按规范设计的结构算例进行精细有限元动力时程分析,验证规范能力措施对控制剪力墙构件出现预期破坏模式的有效性和可行性,并对其改善措施进行了试算对比分析,给出相应的设计建议,并被2010版新规范修订时采纳。

1 现有剪力墙抗震能力设计措施对比分析

RC剪力墙构件能力设计的基本目标是引导剪力墙底部一定区域发生弯曲破坏,并对此区域采取严格的针对性延性保障措施以保证其具有足够的塑性转动能力,其他部位不出弯曲铰;并且采取措施保证剪力墙任何部位都不发生剪切失效,从而使得结构的破坏具有较好的可控性和耗能性。其主要措施是增大底部加强区以上的剪力墙设计弯矩和增大剪力墙所有部位的剪力设计值。对于剪力墙构件抗震设计主要有以下3种方法:

1)美国规范方法[14]:按设计地震作用组合下的计算弯矩进行抗弯承载力设计(如图1(a)),采用极限剪力作为设计值保证不出现剪切破坏(图2(a));

2)新西兰[15]和欧洲[16]规范方法:对剪力墙底部加强区段取基底最大设计弯矩(如图1(b))进行抗弯承载力验算,其上部楼层剪力墙取直线分布弯矩进行抗弯承载力设计。为了保证“强剪弱弯”,欧洲规范考虑弯曲超强对剪力墙剪力计算值乘以不小于1.5的增大系数,对框剪结构等双重结构体系取如图2(b)中设计剪力包络,对剪力墙1/3高度以上考虑高振型影响取值较大,顶部剪力设计值不小于底部设计值的一半;新西兰规定剪力设计值 Vu=ωvφo,w vE,如图2(c)所示,其中 ωv为和结构基本周期相关的动态剪力放大系数,以30层结构为例,ωv为2.3,φo,w为弯矩超强系数,一般大于1.4;

3)中国规范方法[3]:①对于一级抗震等级设计的剪力墙各截面弯矩设计值,底部加强部位及其上一层应按墙底截面弯矩计算值采用,其他部位可按墙肢组合弯矩计算值的1.2倍采用,如图1(c)所示;②对于底部加强部位(1/8结构高度和底部2层的较大值)剪力设计值在一、二和三级抗震等级时分别放大1.6、1.4和1.2倍,如图2(d)所示,对于9度区按实配调整,以保证剪力墙构件“强剪弱弯”性能。

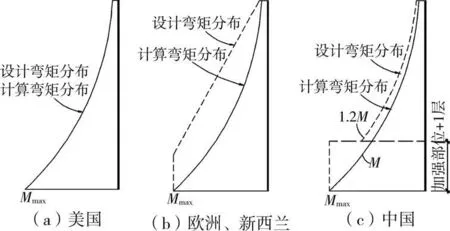
图1 剪力墙抗弯能力调整措施示意

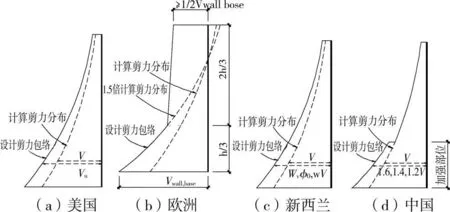
图2 剪力墙抗剪能力调整措施示意

可见,各国规范都采用了一定的“强剪弱弯”措施以保证剪力墙在达到所需的弹塑性弯曲变形之前不发生剪切破坏,但具体措施差别较大,新西兰规范剪力增大系数相对最大,常大于2.0;欧洲规范对底部1/3结构高度的剪力设计值放大1.5倍,对其以上部位放大较多;中国规范对底部加强部位剪力设计值进行了放大,但对加强部位以上的剪力墙剪力未进行放大。在剪力墙抗弯能力设计方面,美国规范方法未对剪力墙计算弯矩进行能力调整,剪力墙破坏部位不易得到控制,沿结构高度范围都可能发生弯曲破坏,不利于采取针对性的延性构造措施;新西兰和欧洲规范除结构底层以外对计算弯矩放大较多;中国规范方法相比欧洲和新西兰方法底部加强部位以上楼层放大系数取较小的定值1.2。

因此,中国规范方法相比国外规范存在的主要问题是底部加强区段上下的弯矩和剪力设计值沿高度有减小的突变,其带来的具体不利影响可能有:

1)底部加强部位及其上一层按墙底截面弯矩计算值采用,可能致使底层外的其他加强部位楼层及加强部位上一层设计弯矩增大较多,在强震中可能不出塑性铰或塑性变形较小,而剪力墙底部截面在强震中塑性变形集中而延性需求可能过大,这种能力设计调整方案未能充分发挥整个底部加强区的塑性变形能力,也使得底部加强区除墙底截面以上部位的延性构造措施未能真正起到作用;

2)剪力墙加强部位以上对其抗弯能力进行了增大,而未对其进行“强剪弱弯”措施调整,其抗剪安全性存在较大隐患,特别是底部加强部位上一层,设计弯矩增大较多,会使其实际能够形成的剪力可能大于其设计剪力导致剪切失效先于弯曲破坏,汶川地震中都江堰有几栋框剪结构在3层及以上出现了剪切裂缝,可能与此有一定的关系。

因此,中国规范关于剪力墙的抗弯和抗剪能力设计措施的有效性需进行验证和改善。为此,下文通过精细有限元动力时程算例对比分析来考察中国规范剪力墙能力设计措施的实际控制效果及提出改进措施。

2 非线性地震反应分析模型

非线性动力时程分析已成为结构抗震性能研究的主要手段之一,得到了广泛的应用。已有研究表明[17],在地震反应分析中采用纤维模型可较合理地模拟框架柱在双向弯曲和变化轴力间的耦合作用;有限元柔度法以单元截面力场的假定作为单元建立的出发点,对于轴向和弯曲变形为主的梁柱单元该假定通常能准确满足,不受单元所处非线性状态的影响,因此能较好地模拟单元进入软化阶段后的强非线性问题。该文采用OpenSees[18](Open System for EarthquakEEngineering Simulation)平台上基于柔度法的梁柱纤维单元模拟框剪结构中的梁和柱。材料对象分别采用基于Scott-Kent-Park的单轴约束混凝土模型和基于Menegotto-Pinto的钢筋模型,保护层和楼板混凝土采用无约束混凝土,梁柱核心区采用约束混凝土;非线性分析时材料强度取平均值;截面采用纤维截面(Fiber Section),单元采用基于柔度法的非线性梁柱单元,单元设置5个积分点,通过单元层次的迭代可确定各控制点的截面抗力和截面刚度,采用Gauss-Lobatto法沿杆长积分计算整个单元的抗力和单元刚度矩阵。

剪力墙的非线性模拟一直是结构动力分析的难点,以往研究多采用宏观模型[19],应用较多的是等效梁模型、三垂直杆元模型和多垂直杆元模型等,但此类模型没有考虑构件的轴向、弯曲效应与剪切效应的耦合,结果依赖于试验结果拟合,精度难以保证,且模型参数较多,定参困难,应用较为麻烦。为了克服这些缺点,吕西林[20]基于框架杆系纤维模型提出了纤维墙元模型,即由承受轴力及弯矩的纤维子单元与承受剪切变形的剪切子单元相合成的墙元计算模型,是对多垂直杆元模型的改进,尽管其仍不能考虑剪力墙弯曲与剪切效应的耦合作用,但其计算结果与试验值吻合较好,可近似模拟剪力墙在地震中的非线性反应,国际上比较流行的IDARC、PERFORM 3D等商用软件中剪力墙构件也采用了这种模型。该文借鉴纤维墙元模型的思想在Opensees分析平台上采用纤维梁柱单元附加剪切子单元来模拟剪力墙,剪力墙构件分析结果与试验吻合较好[21]。

3 算例设计

按中国2001版抗震规范设计8度0.3 g区3×3跨12层框剪结构,Ⅱ类场地,设计地震分组为第一组,底层层高3.9m,其他层层高3.3m,跨度 6m,图3给出其平面布置示意图。Y向左右各布置一道剪力墙,剪力墙长度6m,算例基本情况见表1。梁混凝土强度等级为C30,柱、墙混凝土强度等级1～6层为C35,7～12层为C30。约束混凝土及钢筋材料参数取值参见文献[23]。剪力墙抗震等级为一级,框架抗震等级为二级,底部加强部位为1～2层。模型中梁边各取6倍板厚范围内的板和板筋参与工作,近似考虑楼板的影响;不考虑土结相互作用,基础底部约束假定为固结。动力时程分析选用6条地震波,其中包括按双频段选波法在强震地震动数据库中选出的3条实际地面运动记录和2条采用ARMA模型拟合相应规范反应谱的人工波,如表2和图4所示。本算例弹性设计剪重比从下到上为8%～16.8%,大于规范要求的4.80%,经Pushover分析计算得到屈服剪重比从下到上为18%～39%,说明该结构算例在大震下具有较高的保有抗侧承载力[22]。

图3 偏心框剪结构算例平面布置示意图

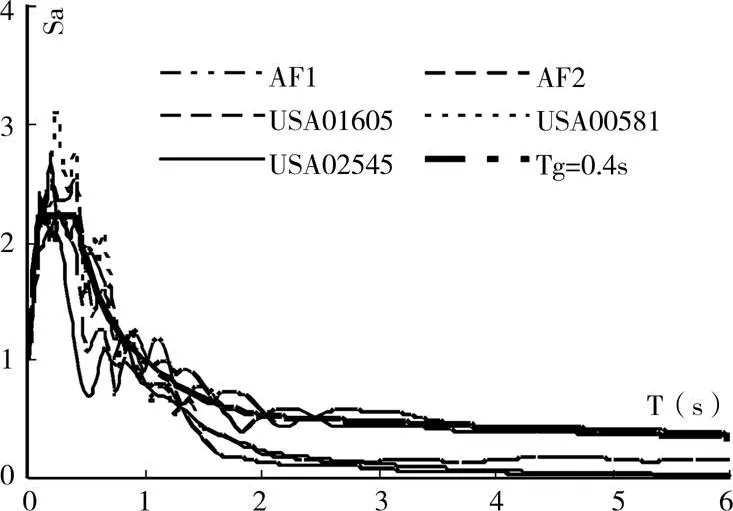
图4 结构算例选用地震波加速度反应谱

表1 12层偏心框剪结构算例基本情况

表2 计算所用地震记录一览表

4 计算结果及分析

4.1 剪切变形的影响

相对梁柱杆件而言,剪力墙的剪切变形不容忽略,剪力墙结构非线性分析结果的可靠性将依赖于剪力墙模型的剪切单元的合理非线性剪切模型及参数的选取,目前应用较多的剪力墙非线性滞回恢复力骨架线如图5所示,各控制点参数的确定用的比较多的是广泽公式[21],其定参过程详见文献[22],但需注意的是,按照广泽公式计算出的屈服承载力有时会显著低于按中国抗震规范公式的计算结果,如表3所示,对于按中国抗震规范设计的剪力墙屈服承载力若按广泽公式计算则会带来抗弯承载力与抗剪承载力的不匹配,导致计算中剪切先于弯曲破坏,因此比较合理的做法是采用规范公式计算剪力墙的屈服承载力,再利用广泽公式提供的其与最大承载力及开裂荷载的比例关系来确定其它参数。剪切滞回曲线捏缩的程度与剪跨比、腹板配筋方式、腹板配筋率、截面正应力水平、混凝土强度等诸多因素相关。鉴于问题的复杂性,参照文献[9]的简化方法处理:取用变形的捏缩系数为0.6,力的捏缩系数为0.25。卸载刚度退化指数β取为0.5,卸载刚度Kd=μ-βks0,μ为延性系数,ks0为初始加载刚度。卸载至0后,反向加载先按上述捏缩系数加载至裂缝闭合点,再按原点指向型加至先前一次最大位移点。

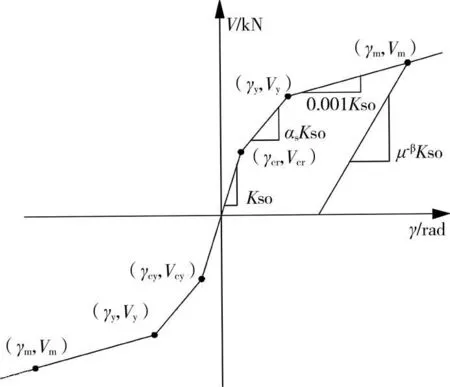
图5 剪力墙骨架曲线示意图

表3 剪力墙剪切参数对比

考虑剪力墙剪切变形与否会显著影响结构地震反应,图6和图7分别给出了剪力墙Q1在大震下(以USA00581为例)的弯曲曲率滞回曲线和层间位移角沿楼层分布。可以看出,考虑剪切变形与否对结构位移反应和构件损伤都有明显的影响,不考虑非线性剪切变形时剪力墙构件的弯曲破坏程度相对严重些,层间位移角相对明显减小。因此,剪力墙结构强震反应分析时必须考虑剪力墙的非线性剪切变形。

限于篇幅,分别以人工波AF1和实际地震动USA00581为例,计算得到的剪力墙Q1的剪切变形值如表4所示,Q1大震下弯曲曲率滞回曲线和剪切变形滞回曲线分别如图8和图9所示。可见,1)采用规范公式确定屈服剪力时,计算得到的剪力墙底部弯曲铰相对更为严重,因为规范公式在墙底部剪切屈服变形比广泽公式大,相应的剪切变形反应小而弯曲变形比重更大;2)采用规范公式定参时,3层剪力墙出现了剪切破坏,屈服系数达到了1.54,这是由于规范对剪力墙底部2层加强部位进行了“强剪弱弯”能力调整,基本能达到要求,但第3层在加大了抗弯能力的情况下不进行强剪弱弯调整则可能造成大震下的剪切失效,而采用广泽公式,底层和3层都发生了剪切破坏,主要是广泽公式计算出的剪切强度在1层明显小于规范公式所致,因此,01规范的剪力墙抗剪能力措施不足以确保其大震下“强剪弱弯”,应对其进行改进。

图6 剪力墙Q1底层墙底在大震下的弯曲曲率滞回曲线(USA00581)

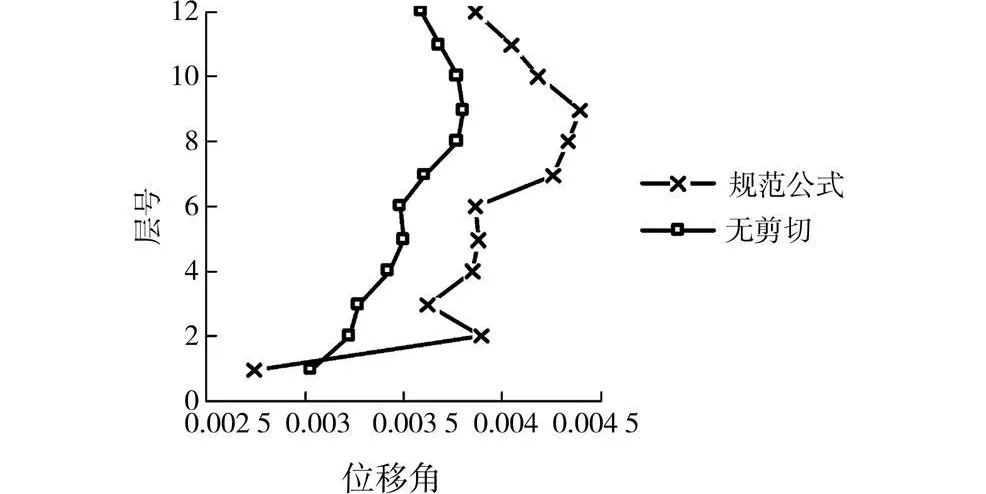
图7 模型L-6层间位移角最大值沿楼层分布(USA00581)

表4 墙Q1剪切变形

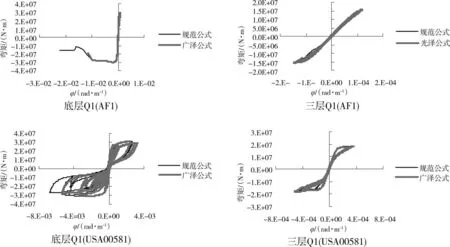
图8 剪力墙Q1在大震下的弯曲曲率滞回曲线

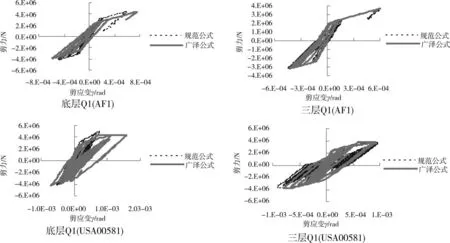
图9 剪力墙Q1在大震下的剪切变形滞回曲线

4.2 抗弯能力措施控制效果

从图8可以看出,人工波大震作用下仅底层墙底发生弯曲屈服,曲率延性系数达到了41,这是剪力墙结构构造措施无法达到的延性需求。图10和表5给出了人工波大震下底层剪力墙底截面钢筋、混凝土最大应变,钢筋最大屈服应变达到0.032,边缘构件范围内混凝土被压溃,墙体轴向承载力迅速降低(如图11(a)所示),丧失稳定的竖向承载能力,甚至其在中震时剪力墙曲率延性系数也达到了4.3;在实际地震波作用下,仍是仅墙底截面屈服,曲率延性约为10～14,但还具有较为稳定的竖向承载力(如图11(b)所示)。

1)人工波比选出的实际地震动计算结果大很多,原因主要是,对于框剪结构算例来说,由于剪力墙提供了大部分刚度,致使其底部出铰后结构周期增大较多,该文算例结构第1周期0.96 s在反应较大时周期变为3.5～5.7 s。而选波时根据弹性反应谱选波法得到的实际地震动在长周期段反应谱明显小于规范反应谱(如图2),而人工波与规范反应谱拟合较好。

图10 墙体钢筋和混凝土应变输出位置示意

图11 剪力墙轴力时程曲线

表5 底层墙Q1钢筋最大应变(AF1)

2)仅在墙底截面出现严重的塑性铰是由于采取的抗弯能力调整措施导致的,说明了第1节中理论分析的正确性。8度0.3g区一级抗震等级的剪力墙一般受地震组合内力控制,剪力墙抗弯承载力超强系数约为1.3(钢筋平均值与设计值之比)×1.3(地震荷载分项系数)×0.85(γRE)=1.436 5,实际上钢筋平均值与设计值的比值1.3还并不能反映剪力墙抗弯承载力增大了1.3倍,实际上由于轴力项的影响承载力并未增大到1.3倍,因此一级剪力墙的底部加强部位超强系数约为1.43,考虑到中震下剪力墙构件开裂后刚度退化周期变长,假设周期变长1.3倍,中震地震作用约减小1.25倍,若实现中震下不屈服则要求抗弯承载力再增大2.86(中震到小震的地震力降低系数)/1.43/1.25=1.6倍。因此,不考虑较软土-结构动力相互作用时,假定墙底固接于地面,剪力墙在大震下甚至是中震下会过早出现塑性铰,而能力调整措施使得除底层截面以外的部位不易出铰,塑性集中在底部截面,导致其峰值反应时曲率延性需求过大,甚至压溃区域过大而丧失稳定的竖向承载能力。根据文献[1],结构位移延性系数μΔ和曲率延性系数μφ存在如下关系:

式中:h w为墙截面长度,H为墙总高。一般根据试验RC墙体在适当构造措施下位移延性系数可达到3～5,因此,算例中的剪力墙曲率延性系数可较为可靠的达到7～14。人工波作用下墙底曲率延性系数41明显超出过多,没有可靠措施能达到这样大的延性需求。因此,应对剪力墙抗弯能力措施进行改进,减小墙底截面过大的延性需求。

需要说明的是,“强墙弱连梁”措施引导连梁出现弯曲塑性铰,是剪力墙结构能力设计的主要措施之一,已有研究较多,该文未对此展开研究,而主要着眼于剪力墙构件自身的能力调整措施的合理性和有效性上,算例大震中连梁弯曲塑性铰曲率延性较大时达到9～15,起到了多道防线的作用,连梁更弱时,连梁塑性耗能相对增大,剪力墙底部损伤会有所减小,但不会改变剪力墙损伤集中在底截面的状况。

4.3 能力措施的改善

为了改善中国2001版规范剪力墙构件在强震中可能存在的剪切失效问题,考虑到中国规范剪力墙底部加强区以上剪力未放大,而国外规范又放大较多,结合中国国情本文取相对折中的剪力加强方案,对剪力墙加强部位设计剪力乘以增大系数1.6,加强部位以上楼层设计剪力取直线变化,结构顶层取计算剪力值,如图12所示,相比国外规范取值偏低,此设计剪力计算出的抗剪钢筋与规范规定的构造配筋取大值,需要说明的是,中国规范对二、三级抗震墙底部加强部位剪力调整系数采用相对较低的增大系数的做法是不合理的,在相同的延性需求下理应采用相同严格程度的延性措施。从剪力墙构件计算剪力分布特征来看,剪力墙中上部抗剪承载力多数由构造配筋控制,对于中下部计算剪力乘以1.4～1.6的增大系数,对于避免剪力墙在强震中由于内力重分布和高振型的影响而发生剪切失效将大有好处。这在后面的算例中将得到证明。

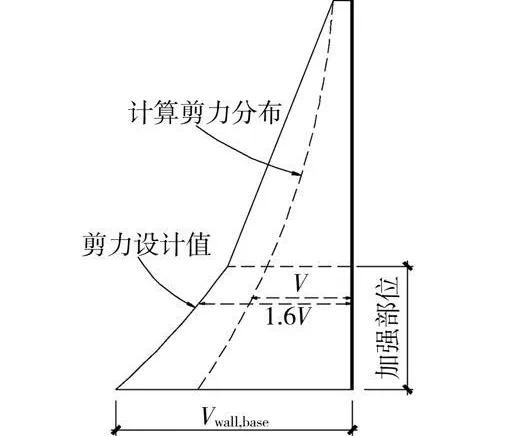
图12 抗剪能力改进措施

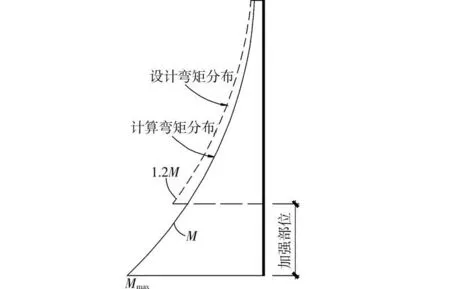
图13 2010版抗震规范剪力墙抗弯能力调整措施

对于解决剪力墙仅在底部截面弯曲延性需求过大的问题,可对剪力墙底部设计弯矩予以放大,但可能会带来屈服部位上移至非加强部位;较为理想的改进措施是将屈服部位控制在底部延性加强区内,尽量使加强区内的截面尽可能多的屈服而耗散能量,减小底截面延性需求,使底部加强区采取的较为严格的延性措施能真正发挥作用。为此设计如表6所示的抗弯能力调整方案进行非线性动力反应分析,考察各措施的有效性。算例R-01和R-02沿袭01抗震规范的思路增大底部加强部位的设计弯矩以期望减小剪力墙底截面的弯曲变形;R-03对剪力墙底部加强部位计算弯矩不进行放大,仅对底部加强部位以上计算弯矩放大1.2倍;R-04和R-05在R-03的基础上对底层计算弯矩进行适当放大。图14给出了各算例剪力墙Q1的弯矩曲率。算例 R-01剪力墙底层底截面屈服仍很严重,曲率延性系数达到了31,第3层屈服程度较轻,曲率延性系数为1.5,其他层剪力墙未屈服;算例R-02剪力墙第1、3和4层发生弯曲屈服,曲率屈服系数分别为2.8、4.8和12.1,说明底部计算弯矩放大后可能导致破坏部位转移到非加强部位,不利于针对性的采取严格的延性构造措施。算例 R-03剪力墙底部加强部位即第1、2层发生弯曲屈服,屈服系数分别为24.1和3.0,底层剪力墙承载力下降到极限承载力的75%,具有较为稳定的竖向承载力(图15(a)所示),其他部位未发生弯曲屈服,相比原01规范措施的控制效果有了明显的改善,但底部延性需求仍较大;算例R-04剪力墙第1、2层屈服系数分别为11.2和26.5,说明1层加强较多后2层屈服程度显著加重,曲率延性需求过大;算例R-05剪力墙第1、2层屈服系数分别为14.5和9.8,极限承载力未下降,具有稳定的竖向承载力(图15(b)所示)。总体来说,R-03和R-05是比较符合将剪力墙弯曲破坏较为均匀的控制在底部加强区范围内的改进措施,2010版新抗震规范即采纳了R-03的改进措施(图13所示),尽管底部截面弯曲曲率仍较大,但考虑到剪力墙结构实际土-结构动力相互作用效应将降低底层剪力墙构件的地震反应,R-03的措施在实际情况中也可能取得较好的效果,可以肯定的是R-03的改进措施比01抗震规范采取的抗弯能力措施更为有效;从该文算例计算结果来看R-05改进措施是符合能力设计要求的最有效措施,究竟哪种抗弯能力改进措施更为有效有待进一步的土-结构动力相互作用分析及结构模型试验研究验证。

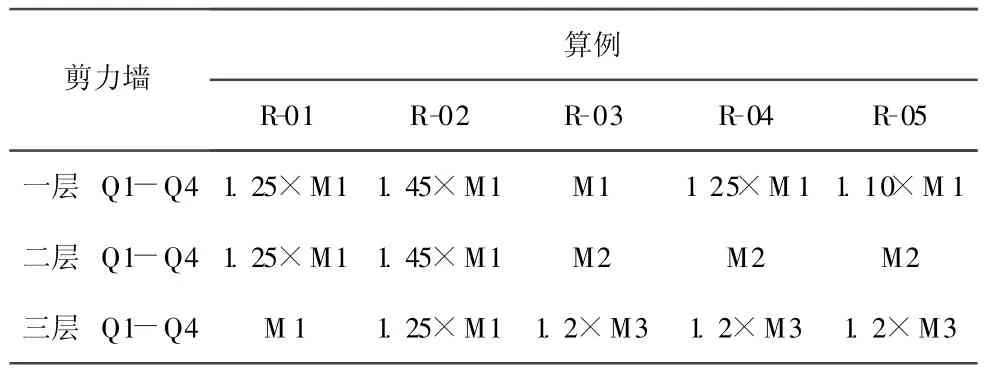
表6 剪力墙抗弯承载力调整方案

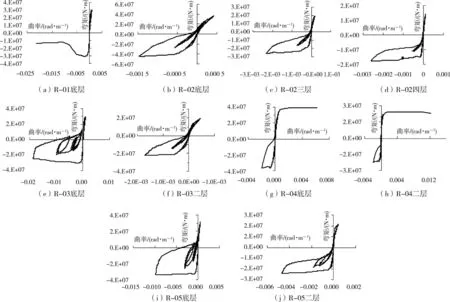
图14 各改进措施算例剪力墙弯矩曲率滞回曲线(Q1)

图15 改进措施剪力墙轴力时程曲线

以R-05为例,图16和图17分别给出采取规范抗剪能力措施和该文建议的改进措施时剪力墙剪切变形滞回曲线。可见,采用规范剪力墙抗剪能力调整措施时,在第3、4层将出现剪切失效;而采用该文提出的抗剪能力调整措施,各层都未出现剪切失效。

图16 算例R-05采取规范抗剪能力调整措施时Q1在大震下的剪切变形滞回曲线

图17 算例R-05采取提出的改进抗剪能力调整措施时Q1在大震下的剪切变形滞回曲线

5 结语

该文指出中国2001版抗震规范的剪力墙能力设计措施存在的问题,通过精细有限元动力时程算例分析,校验了中国规范剪力墙能力调整措施控制其预期破坏模式的有效性;提出了改进措施,并进行了算例验证,得到的主要结论有:

1)中国2001版抗震规范采用的剪力墙抗震能力设计措施理论上存在不足,亟需改进。在刚性地基假定下的算例分析表明,剪力墙底截面弯曲延性需求过大、竖向承载力丧失,而底部延性加强区其他部位不屈服,未充分发挥底部延性加强区塑性耗能的目的;现行规范采用的抗剪能力措施不能避免底部加强区以上剪力墙楼层剪切失效。

2)对剪力墙抗弯能力设计改进措施的算例对比分析表明,对剪力墙底部加强部位以上进行抗弯能力增大调整、底部加强区除底截面外不进行调整,可引导剪力墙弯曲屈服较为均匀的出现在底部延性加强区内,2010版抗震规范采用的改进措施相比目前国外各国抗震规范更为合理。

3)提出了剪力墙抗剪能力设计改进措施,即对剪力墙加强部位设计剪力乘以增大系数1.6(不区分抗震等级),加强部位以上楼层设计剪力取直线变化,结构顶层取计算剪力值,设计剪力计算出的抗剪钢筋与规范规定的构造配筋取大值,通过算例分析表明其可有效避免剪力墙底部加强区以上楼层强震中出现剪切失效。

4)剪力墙屈服后结构周期变大较多,按弹性反应谱双频段选波法选出的实际地震波比拟合规范反应谱的人工波大震计算结果小很多,结构强震非线性动力时程分析时选波原则和方法需进一步开展研究。

5)该文针对剪力墙抗震能力设计措施开展了一些初步研究,提出的改进措施在理论上更为合理,但其有效性还有待进一步深入的土-结构动力相互作用分析及结构模型试验研究进行验证。

[1]鲍雷◦T,普里斯特利M◦J◦N.钢筋混凝土和砌体结构的抗震设计[M].北京:中国建筑工业出版社,2002.

[2]叶列平,曲哲,陆新征,等.提高建筑结构抗地震倒塌能力的设计思想与方法[J].建筑结构学报,2008,29(4):42-50.YELIE-PING,QU ZHE,LU XIN-ZHENG,et al.CollapsEprevention of building structures:a lesson from thEWenchuan earthquake[J].Journal of Building Structures,2008,29(4):42-50.

[3]GB 50011-2001建筑抗震设计规范[S].北京:中国建筑工业出版社,2001.

[4]王亚勇.汶川地震建筑震害启示——三水准设防和抗震设计基本要求[J].建筑结构学报,2008,29(4):26-33.WANG YA-YONG.Lessons learnt from building damages in thEWenchuan earthquake:threeearthquakEperformancEobjectives and basic requirements for seismic design of buildings[J].Journal of Building Structures,2008,29(4):26-33.

[5]谢礼立.汶川地震的教训[J].南京工业大学学报:自然科学版,2009,31(1):1-8.XIELI-LI.Lessons learnt from Wenchuan earthquake[J].Journal of Nanjing University of Technology:Natural SciencEEdition,2009,31(1):1-8.

[6]韩军,李英民,姬淑艳.RC框架结构合理破坏机制的实现[J].哈尔滨工业大学学报,2010.42(12):1559-1565.HAN JUN,LI YING-MIN,JI SHU-YAN.Realization of rational failuremechanism for thERCframEstructure[J].Journal of Harbin InstitutEof Technology,2010.42(12):1559-1565.

[7]林旭川,潘鹏,叶列平,等.汶川地震中典型 RC框架结构的震害仿真与分析[J].土木工程学报,2009,42(5):13-20.LIN XU-CHUAN,PAN PENG,YELIE-PING,et al.Analysis of thEdamagemechanism of a typical RC framEin Wenchuan Earthquake[J].China Civil Engineering Journal,2009,42(5):13-20.

[8]单慧敏,戴君武,王艳茹.现浇楼板对钢筋混凝土框架结构破坏模式影响浅析[J].土木工程学报,2010,43(S1):169-172.SHAN HUI-MIN,DAI JUN-WU,WANG YAN-RU.Effects of casting slabs on thEfailuremodEof RC framEstructure[J].China Civil Engineering Journal,2010,43(S1):169-172.

[9]韦锋,陈文科,傅剑平,等.8度区框-剪结构中框架在罕遇地震下的反应性态[J].土木建筑与环境工程.2009,31(6):60-65.WEI FENG,CHEN WEN-KE,FU JIAN-PING,et al.Seismic behaviors of f rames in frame-wall structures under rarEearthquakes on thEzonEof fortification intensity 8 in China[J].Journal of Civil Architectural&Environmental Engineering,2009,31(6):60-65.

[10]季静,韩小雷,郑宜,等.基于能力设计原理的双肢剪力墙极限承载力研究[J].地震工程与工程振动,2006,26(4):114-120.JI JING,HAN XIAO-LEI,ZHENG YI,et al.Analysis of ultimatebearing capacity of coupled shear walls based on philosophy of capacity design[J].EarthquakEEngineering and Engineering Vibration,2006,26(4):114-120.

[11]胡庆昌.钢筋混凝土框剪结构抗震设计若干问题的探讨[J].建筑结构,2006,36(6):84-86.HU QING-CHANG.SomEproblems relating to seismic design of RC frame-wall structure[J].Building Structure,2006,36(6):84-86.

[12]SULLIVAN,TIMOTHY J.Capacity design considerations for RC frame-wall structures[J].EarthquakEand Structures,2010,1(4):391-410.

[13]BOIVIN Y,PAULTREP.Seismic performancEof a 12-storey ductilEconcreteshear wall system designed according to thEnew Canadian building design codes[C]//Proceedings,Annual Conference-Canadian Society for Civil Engineering,JunE10,2008,Quebec City,Canada.

[14]ACI 318-05 Building CodERequirements for Structural Concrete[S].American ConcretEInstitute,2005.

[15]NZS3101 New Zealand Standard CodEof PracticEfor thEDesign of ConcretEStructures[S].Standard Association of New Zealand,1995.

[16]Eurocode8:Design of Structures for EarthquakEResistance[S].European Committeefor Standardization,2003.

[17]FABIO F TAUCER,ENRICO SPACONE,FILIPC FILIPPOU.A Fiber Beam-Column Element for Seismic ResponsEAnalysis of Reinforced ConcretEStructures[R].Berkeley:UCB/EERC-91/17,1991.

[18]MAZZONI SILVIA,MCKENNA F,SCOTTm H,et al.OpenSees Usersmanual[R].Berkeley:PEER,University of California at Berkeley,2006.

[19]YIHAI BAO,SASHI kKUNNATHA.Simplified progressivEcollapsEsimulation of RC frame-wall structures[J].Engineering Structures,2010,32:3153-3162.

[20]吕西林,卢文生.纤维墙元模型在剪力墙结构非线性分析中的应用[J].力学季刊,2005,26(1):72-80.LvXI-LIN,LU WEN-SHENG.Application of fiber wall elementmodel in nonlinear analysis of shear wall structures[J].ChinesEQuarterly ofmechanics,2005,26(1):72-80.

[21]臧登科.纤维模型中考虑剪切效应的RC结构非线性特征研究[D].重庆:重庆大学,2008.

[22]叶列平,孙玉平.日本钢筋混凝土结构的大震设计方法介绍[J].建筑结构,2009,40(6):114-118.YELIE-PING,SUN YU-PING.Introduction of designmethod for RC structures under severEearthquakEin Japan[J].Building Structure,2009,40(6):114-118.

[23]韩军.建筑结构扭转地震反应分析及抗扭设计方法研究[D].重庆:重庆大学,2009.