小跨高比混凝土简支箱梁静力性能试验研究

陈朝晖,黄景华,李观宇,马东升

(1.重庆大学 a.土木工程学院;b.山地城镇建设与新技术教育部重点实验室,重庆400045;2.云南省电力设计院,昆明 650051;3.华北电力设计院工程有限公司,北京100120)

箱形截面具有良好的结构性能,在现代各种桥梁中得到广泛的应用[1]。因其对地基不均匀沉降有很好的适应性,断面形式方便调节,施工简单且容易保证质量等优点,钢筋混凝土箱涵也是大型输水工程中常见的构造形式[2]。与传统的矩形截面梁相比,混凝土薄壁箱梁的弯曲正应力沿翼板宽度的分布不均匀,存在剪力滞现象[3-10]。Luo[11]等利用有机玻璃模型制作了变截面高度箱梁模型,研究了变高度对剪力滞的影响。Khaled Galal[12]等进行了加腋薄壁钢筋混凝土箱梁的试验研究,指出了偏心荷载和底板对箱梁极限承载力的影响,箱梁破坏机制和荷载-位移曲线等。方志等[13]进行了钢筋混凝土连续宽箱梁的破坏全过程试验,研究了连续箱梁在混凝土开裂后的内力重分布变化规律。祝明桥等[14]进行了体外预应力高强混凝土薄壁箱梁从预应力钢绞线张拉至承载力极限的破坏过程,研究了体外预应力箱梁的抗裂性能。杨春、蔡健[15]等研究了箱形型钢混凝土(SRC)梁的性能,给出了箱形SRC组合梁的抗剪承载力计算公式。牛斌等[16]进行了铁路客运专线24m预应力混凝土双线整孔箱梁1∶2模型进行试验和理论研究,结果表明影响箱梁剪力滞系数的主要因素是箱梁的宽跨比及荷载形式。

前述文献集中在对跨高比较大的箱形梁的研究,对腹板间距小、截面高度大、跨高比较小的深受弯箱形梁研究欠缺。重庆市排水干管为满足设计流量的要求、便于结构施工等,采用高而窄的矩形箱涵,跨高比在2.6至4.3之间,为深受弯构件。其中埋地箱涵段一般敷设在边坡上,在正常情况下,由于四周土壤的约束,箱涵的受力与变形都较小,但在强降雨下,边坡容易发生滑坡、坍塌,埋地箱涵下方的土壤发生下陷或流失,形成以两端柱墩支撑的简支箱梁,箱梁上方覆土自重作为外荷载作用于箱梁上,对于按埋地形式设计的管道在这种特殊的荷载工况下受力与变形极为不利。因此,本文对此类小跨高比箱梁的受力性能进行了试验研究。

1 模型试验概况

1.1 试验梁的设计

以重庆市排水主干管埋地箱涵为原型,制作了2根缩尺比为1∶5的钢筋混凝土箱梁进行静力加载试验。试验梁高为700mm,总长2 400mm,壁厚80mm,截面尺寸及配筋如图1所示。钢筋及混凝土的力学性能分别如表1、2所示。其中,混凝土的抗压强度 f cu在试验前一天测得,是与试件同条件养护的一组3个 150mm立方体试块的均值,f c=0.76f cu,f t=0.26f2/3cu。

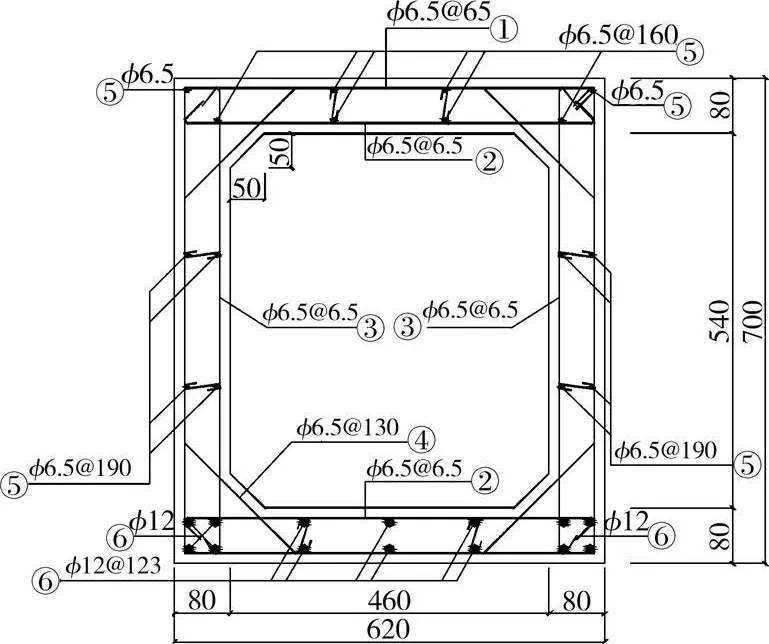
图1 试验梁截面尺寸及配筋

表1 钢筋的力学性能

表2 混凝土的力学性能

1.2 试验方法

在强降雨下,边坡容易发生滑坡、坍塌,埋地箱涵下方的土壤发生下陷或流失,形成以两端柱墩支撑的简支箱梁,箱梁上方覆土自重作为外荷载作用于箱梁上,为模拟此不利工况,试验的箱梁端部一侧采用转动支座,另一侧采用滚动支座以模拟简支约束。由于试验箱梁跨度小,通过在横向分配梁下设置两个面积较大、刚度大的橡胶垫,使得由千斤顶传递下来的荷载较均匀地施加在箱梁上,试验梁加载装置如图2所示。

图2 试验梁加载装置

1.3 测点布置

利用试验梁的对称性,以试验梁跨中截面(1-1)、一侧的加载点截面(2-2)作为控制截面,在控制截面的纵筋上沿梁跨方向布置纵筋应变片。在试验梁剪跨区段的箍筋沿支座-加载点连线(OA)以及45度斜线(OB)布置箍筋应变片,如图3所示。跨中截面腹板范围内的底板布置2个百分表,用于测量试验梁底部的挠度。剪弯段布置4个百分表,用于测量该区段的剪切变形及弯曲变形[17],如图2所示。

图3 钢筋应变片布置及编号

2 试验结果分析

2.1 破坏形态

各试验梁所经历的裂缝发展过程基本相同。总荷载至0.2Pu(Pu为计算极限荷载)左右时,剪弯段腹板中部首先出现多条不连续的腹剪斜裂缝。加载至0.3Pu时,纯弯段底板出现多条小的弯曲裂缝。荷载加至0.4Pu时,底板继续不断出现弯曲裂缝,加载点截面附近的部分弯曲裂缝发展成为弯剪斜裂缝,同时剪弯段则出现新的腹剪斜裂缝平行于既有的腹剪斜裂缝。荷载增加至0.5Pu时,腹板上部出现水平裂缝。加载到0.7Pu左右时,腹剪斜裂缝之间的不断出现细小的裂缝,支座与加载点连线的混凝土有压碎的倾向,其他裂缝发展宽度增加,长度基本不变。荷载达到Pu时,没有明显的临界斜裂缝产生,最终由于混凝土斜向受压柱压溃而丧失承载力,开始进入下降段。与桥梁工程中常见的跨高比大的箱形梁,在极限荷载下伴随着下翼板钢筋屈服、上翼板混凝土压碎而发生弯曲破坏不同,本试验箱梁跨高比较小,剪切效应明显,从试验梁破坏的裂缝形态可以看出,试验梁已呈现出一定的拱受力机制。上部未开裂混凝土可视为拱,荷载通过此拱效应传入支座,受拉钢筋则形成拱的拉杆,最终为斜向主拱肋中混凝土被裂缝分割成若干个斜向短柱而压溃引起试验梁破坏,为典型的斜压型剪切破坏。

图4 试验梁裂缝形态图

埋地箱涵原本由连续地基支承,地基对箱涵产生竖直向上的地基反力,抵消了部分竖直向下的荷载,对管道结构是有利的。但由于滑坡导致地基塌陷,地基与箱涵分离,造成支承条件改变,箱涵不再有竖直向上的地基反力,上覆土壤自重荷载全部由简支架空箱涵本身承担,导致混凝土过早开裂,影响排水管道正常使用。

利用非线性有限元分析软件ABAQUS模拟有地基支承的箱梁,其中混凝土和钢筋分别采用C3D8R单元和T3D2单元,混凝土材料采用损伤塑性本构模型,钢筋采用理想弹塑性模型,不考虑钢筋与混凝土的粘结滑移。支座采用铰支约束(U1=U2=U3=0),基床系数取30 000 kN/m3,采用位移加载。结果显示当总荷载P=58.8 t时,剪弯段腹板中部混凝土首先开裂;箱梁极限承载力为168.8 t。与上述试验箱梁工况对比:当P=24 t时,剪弯段腹板中部首先出现多条不连续的腹剪斜裂缝;加载到P=28 t时,在跨中附近出现第一条弯曲裂缝;箱梁极限承载力为102 t。可见,由于滑坡导致地基塌陷使埋地箱涵成为简支箱涵,支承方式的改变导致箱涵混凝土过早开裂,结构的承载力大幅降低,影响管道的正常使用。

2.2 刚度变化

试验梁的荷载-跨中截面挠度曲线如图5所示。可见,2个构件均发生剪切破坏,破坏时的挠度均比较小。达到极限承载力之前,荷载-位移曲线近似为直线,抗弯刚度基本没有变化。达到极限承载力之后,构件刚度开始降低。虽然构件随着箍筋屈服混凝土斜向压溃而最终发生剪切破坏,但是由于纵筋配筋率较大,刚度下降比较缓慢,使最终破坏时的跨中挠度较大,呈塑性破坏。

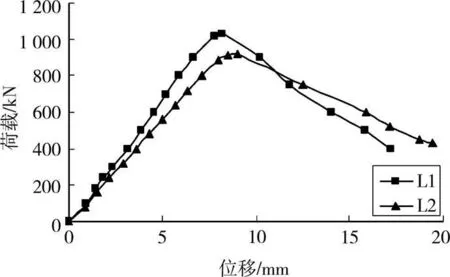
图5 荷载-位移曲线

剪弯段的荷载-剪切角如图6所示,显示出如下规律:

图6 荷载-剪切角曲线

1)混凝土未开裂前,构件的剪力主要由混凝土承担,构件剪弯段的剪切角基本没有变化。刚出现腹剪斜裂缝时,裂缝宽度较小,此时尚有沿斜裂缝的混凝土骨料咬合作用,开裂之时剪切变形并未急剧增加。当裂缝开展到一定宽度后,受粒径影响,骨料咬合力急剧减小,构件的抗剪刚度亦急剧减小,剪切变形急剧增加。

2)实测的L2的混凝土强度低于L1,使得L2的荷载-剪切角曲线突变时的荷载值小于 L1,同一级荷载下L2的剪切角大于L1,说明混凝土强度对构件抗剪刚度的影响较大。

2.3 钢筋受力分析

2.3.1 箍筋受力分析 从图7剪弯段箍筋荷载-应变曲线可以得出以下结论:

图7 箍筋荷载-应变曲线

1)加载初期,剪力主要由混凝土承担,所以箍筋在斜裂缝未形成之前应变较小且增长幅度不大。荷载达到200 kN左右时,斜裂缝通过箍筋,箍筋承担了较多的剪力,从而使多数箍筋应变骤增;

2)部分箍筋最终达到屈服应变,大多是靠近梁的中部即裂缝最宽处的箍筋首先屈服,之后相邻的箍筋相继屈服;因为斜裂缝的位置和开展程度不同,同一根箍筋的应力沿长度的分布也是不均匀的。

2.3.2 纵筋受力分析 从图8箱梁的纵筋荷载-应变曲线中可以得出如下结论:

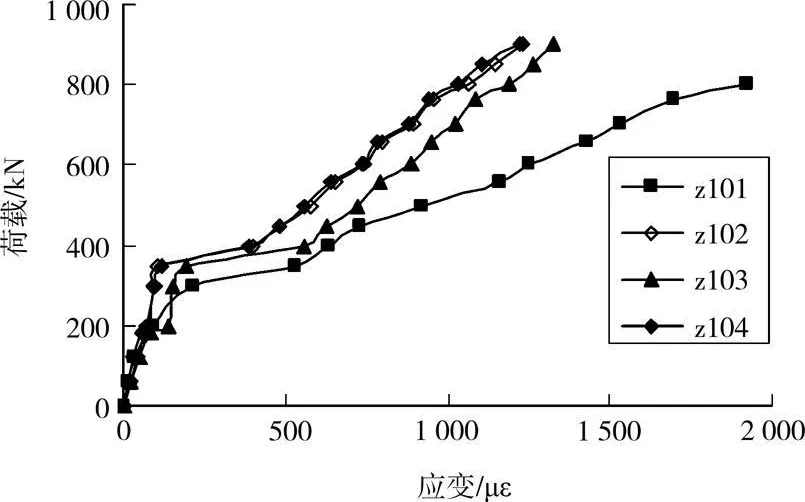
图8 跨中翼板纵筋荷载-应变曲线

1)荷载值较小时,翼板纵筋应变基本为线性增长,应变值较小。当荷载达到380 kN左右时,跨中翼板纵筋荷载-应变曲线出现突变,斜率急剧下降,应变突变值为300～400με之间。纵筋应变的突然增加主要是因为随着荷载的增加,箱梁翼板混凝土实际拉应变大于混凝土极限拉应变,产生弯曲裂缝,有效截面高度减少,钢筋应力急剧增加,因此钢筋应变急剧增加。但是纵筋出现突变时的荷载值晚于箍筋出现突变时的荷载值,说明剪力效应明显,构件先在腹板中部出现腹剪斜裂缝,然后在翼板处出现弯曲裂缝。

2)破坏时,少数翼板纵筋屈服,其屈服荷载大于箍筋的屈服荷载;说明箱梁剪力效应明显,呈剪切破坏,而非弯曲破坏。

从纵筋应变沿翼板宽度的分布图(图9、10)可以看出,混凝土开裂前,腹板范围内的翼板纵筋拉应变比较大,翼板中间纵筋的应变值总体呈现出减小的规律,即产生了正剪力滞现象。剪力滞效应主要受翼板宽度和腹板高度的影响,上下翼板愈宽,腹板高度愈低,剪力滞效应愈突出。而此类箱梁跨高比小,属于深受弯构件,腹板间距比较小,截面高度比较大,有别于桥梁工程中常见的宽矮箱梁,翼板受剪切变形影响小,而试验加载方式导致跨中部分是无剪力区段。此外,由于跨中翼板混凝土开裂后,跨中翼板纵筋测点处钢筋应力受截面内力重分布及翼板裂缝分布形式影响,翼板中央处纵筋应变比较大,而腹板范围内的翼板纵筋应变反而小,没有出现明显剪力滞现象,如图9所示。

图9 混凝土开裂前后跨中翼板纵筋应变分布

图10 加载点截面翼板纵筋应变分布

由箱梁跨中腹板应变沿高度的分布(图11)可见,开裂前截面应变基本符合平截面假定,开裂后则不再符合平截面假定。开裂前,钢筋和混凝土的应变较小,箱梁截面应变分布基本呈线性分布;开裂后,对受压区而言,混凝土的应变基本还是线性分布,但是由于此箱梁截面高度大,受压区高度小,受拉区混凝土与钢筋之间已发生较大的相对滑移,且随着荷载增加,屈服的钢筋增多,裂缝加宽和截面转角增大的速度呈非线性增长,截面应变不再是线性分布。因此,对于跨高比较小的深受弯箱梁在混凝土开裂后平截面假定不再适用。

图11 跨中腹板纵筋应变分布

2.4 斜截面受剪承载力分析

钢筋混凝土受弯构件斜截面抗剪承载力主要受剪跨比(跨高比)、混凝土强度、配箍率、纵筋配筋率、尺寸效应和形状、受压翼缘等因素影响。小跨高比钢筋混凝土简支梁承受横向荷载时,一般可将上部未开裂混凝土视为拱,荷载通过此拱效应传入支座,受拉钢筋则形成拱的拉杆,梁的剪切破坏是由斜向主拱肋中混凝土的压溃所引起的。目前各国规范对箱梁斜截面受剪承载力均无成熟的计算方法,我国《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG-D 62-2004)[18]将箱形梁简化为工字梁计算其斜截面抗剪承载力,具体公式为:V=α1α2α30.45×其中(α1 为异号弯矩影响系数;α2为预应力提高系数;α3为受压翼缘的影响系数;fcu,k为混凝土强度等级;ρsv为斜截面内配箍率;f sv为箍筋抗拉强度设计值;P为斜截面内纵向受拉钢筋的配筋百分率,P=100ρ;b为腹板宽度;h0为正截面有效高度),据此计算得到试验箱梁抗剪承载力为443 kN。上述计算方法主要考虑了混凝土强度、配箍率、纵筋配筋率和受压翼缘的影响,而忽视了剪跨比的影响。研究表明,剪跨比不同导致剪切破坏类型不同,由此产生的抗剪承载力也有较大区别,以斜压破坏抗剪承载力最大,剪压破坏次之,斜拉破坏最小。实验显示,此类城市排水干管闭合箱梁是典型的斜压型破坏,其抗剪承载力均值高于490 kN。可见,中国现行桥涵设计规范低估了此类箱梁的承载力,设计偏保守。

中国现行《混凝土结构设计规范》[19]同样将箱梁视为T形或I形截面梁计算其抗剪承载力,计算公式为,据此得到的试验箱梁斜截面受剪承载力计算值为V=540 kN。公式中虽然考虑了跨高比、混凝土强度、配箍率、纵筋配筋率等因素影响,但其计算值比试验结果约高10%,究其原因在于:1)试验箱梁属于薄壁构件,容易在较薄弱一侧腹板先开裂。2)箱梁在加载过程中存在“框架效应”,箱形截面像“箱形框架”一样受力,腹板发生弯曲外凸,处于弯剪耦合状态,降低了箱梁的抗剪承载力。3)计算公式中没有考虑剪力滞的影响。因此,采用该设计规范公式高估了实际箱梁的抗剪承载力。

可见,现行桥梁设计规范和混凝土设计规范对于深受弯薄壁箱梁斜截面受剪承载力的计算均存在不足,应予以重视。

3 结论

对山地城市排水干管中的埋地箱涵由于滑坡地基塌陷造成支承条件改变后的性能进行了模型静力加载试验,分析了简支条件下小跨高比埋地箱梁的破坏形式、抗剪性能以及剪力滞效应,初步讨论了现行有关设计规范对箱涵抗剪承载力计算之不足,得出以下几点主要结论:

1)在竖向均布荷载下,小跨高比简支箱梁的破坏形态表现为剪切破坏,裂缝主要集中在剪弯段,纯弯段只有少许弯曲裂缝。裂缝分布比较广泛,破坏时没有出现明显的临界斜裂缝。

2)斜裂缝未形成之前箍筋应变较小且增长幅度也不大。混凝土开裂后,裂缝穿过区域的箍筋应变值突然增大,最终使部分箍筋达到屈服,箍筋在混凝土开裂之后承担了较多的剪力,为主要的抗剪部件。

3)1/4跨翼板以及混凝土开裂前的跨中翼板纵筋应变呈现明显的剪力滞效应。但是由于该箱梁腹板间距较小,截面高度较大,混凝土开裂后的跨中翼板纵筋受截面内力重分布及翼板裂缝分布形式等因素影响,混凝土开裂后跨中翼板没有明显的剪力滞现象。

4)混凝土开裂前,截面应变基本符合平截面假定,开裂后则不再符合平截面假定。

5)强降雨致边坡滑坡、坍塌等地质灾害使原来按埋地管道设计的箱涵变成了两端简支的架空箱梁。支承方式的改变,使箱涵结构混凝土过早开裂,结构承载力大幅降低,而我国现行有关规范对于深受弯薄壁箱梁斜截面受剪承载力的计算均存在不足,应予以重视。

因此,为了防止排水管道结构性破坏而导致污水渗漏污染环境,影响排水管道的正常运营。应做好管道沿线边坡治理、加强边坡监测以保障管道安全运营。

[1]郭金琼,房贞政,郑振.箱形梁设计理论[M].北京:人民交通出版社,2008.

[2]何辉,杨志刚,王国涛.长距离输水中混凝土箱涵开裂过程分析[J].海河水利,2006(2):63-66.HEHUI,YANG ZHI-GANG,WANG GUO-TAO.Cracking analysis for reinforced concretEbox girder in long-distancEwater diversion[J].HaihEWater Resources,2006(2):63-66.

[3]张士铎,邓小华,王文州.箱形薄壁梁剪力滞效应[M].北京:人民交通出版社,1998.

[4]罗旗帜,吴幼明.薄壁箱梁剪力滞理论的评述和展望[J].佛山科学技术学院学报:自然科学版,2001,19(3):29-35.LUO QI-ZHI,WU YOU-MING.Comments and prospect on thEtheories of thEshear lag in thin-walled box girders[J].Journal of Foshan University:Natural SciencEEdition,2001,19(3):29-35.

[5]KUZMANOVIC BO,GRAHAM H J.Shear lag in box girders[J].J.Struct.Div.,ASCE,1981,107(9):1701-1712.

[6]FOUTCH D A,CHANG PC.A shear lag anomaly[J].J.Struct.Engrg.,ASCE,1982,108(7):1653-1658.

[7]ALGHAMDI S A.Static andmodal analysis of thinwalled box girder structures[J].AIAA Journal,2001,39(7):1406-1410.

[8]ERKMEN R E,MOHAREBm.Torsion analysis of thin-walled beams including shear deformation effects[J].Thin-Walled Structures,2006,44:1096-1108.

[9]LUO Q Z,LIQ S,Shear lag of thin-walled curved girder bridges[J].Engineeringmechanics(ASCE),2000,126(10):1111-1114.

[10]周世军.箱梁的剪力滞效应分析[J].工程力学,2008,25(2):204-208.ZHOU SHI-JUN.Shear lag analysis of box girders[J].Engineeringmechanics,2008,25(2):204-208.

[11]LUO Q Z,WU Ym,TANG J,et al.Experimental studies on shear lag of box girders[J].Engineering Structures,2002,24(4):469-477.

[12]GALAL K,YANG QING.Experimental and analytical behavior of haunched thin-walled RC girders and box girders[J].Thin-Walled Structures,2009,47(2):202-218.

[13]曹国辉,方志.钢筋混凝土连续宽箱梁受力性能试验[J].中国公路学报,2006,19(5):46-52.CAO GUO-HUI,FANG ZHI.Mechanical behaviors test of RCcontinuous box girder with widEflange[J].China Journal of Highway and Transport,2006,19(5):46-52.

[14]祝明桥,方志,胡秀兰.体外预应力高强混凝土薄壁箱梁试验研究[J].中国公路学报,2004,17(3):25-30.ZHUmING-QIAO,FANG ZHI,HU XIU-LAN,et al.Experimental research on thEexternally prestressed high-strength concretEthin-walled box girder[J].China Journal of Highway and Transport,2004,17(3):25-30.

[15]YANG CHUN,CAI JIAN.Experimental study on box shapEsteel reinforced concretEbeam[J].Journal of Southeast University,2005,19(2):25-36.

[16]牛斌,杨梦蛟,马林.预应力混凝土宽箱梁剪力滞效应试验研究[J].中国铁路科学,2004,25(2):25-30.NIU BIN,YANGmENG-JIAO,MA LIN.Shear lag effect test and study of PC widEbox beam[J].China Railway Science,2004,25(2):25-30.

[17]刘光伟.小跨高比剪力墙洞口连梁抗震性能试验研究[D].重庆:重庆大学,2006.

[18]JTGD 62-2004公路钢筋混凝土及预应力混凝土桥涵设计规范[S].北京:中国铁道出版社,2004.

[19]GB 50010-2002混凝土结构设计规范[S].北京:中国建筑工业出版社,2002.