钢管混凝土柱-钢梁外环板节点抗弯承载力计算方法

王文达,秦 庚,张鹏鹏

(兰州理工大学 a.甘肃省土木工程防灾减灾重点实验室;b.土木工程学院,兰州 730050)

钢管混凝土柱-钢梁外加强环板式节点在多高层钢管混凝土框架结构中应用越来越广,该类节点具有传力明确、刚度大、塑性性能好、承载力高等优点[1]。《矩形钢管混凝土结构技术规程》[2]和《钢管混凝土结构技术规程》[3]中对于该类节点的设计有相关条文,但多限于环板尺寸的计算,而对其抗弯承载力的计算暂没有规定,规程[2]也仅提供了带内隔板的矩形钢管混凝土柱与钢梁刚性焊接节点抗弯及抗剪承载力验算公式,而对于工程中广泛应用的外环板节点则没有给出相关公式。国内外研究者对此类节点的力学性能已进行了相关的试验及理论研究,例如 Thom ann 等[4]、Shin 等[5]、Cheng等[6]、Li等[7]、Choi等[8]、Wang 等[9]、王 文达 等[10]、陈娟等[11]、李成玉等[12]等。上述研究主要集中在环板节点整体的刚度及抗震性能方面,对节点核心区的力学性能及其抗弯及抗剪承载力的研究并不多见。节点设计一般需满足“强柱弱梁、节点更强”的原则,框架结构可能出现的屈服机制有梁端塑性铰模式、柱端塑性铰模式及节点核心区塑性铰模式,为满足框架结构在各种作用下的合理屈服机制和破坏模式,必须避免会造成严重后果的节点屈服模式,节点更应满足“强节点强锚固”的要求。节点的抗弯及抗剪承载力计算方法是进行节点承载力验算的依据,例如为保证满足“强节点”的设计要求,现行抗震设计规范中规定了钢筋混凝土框架梁柱节点核心区的承载力验算方法。相比较而言,目前对钢管混凝土柱-钢梁节点的抗弯及抗剪承载力设计计算公式的研究很少,相关规范中也没有具体条文,因此难以准确地评估节点核心区的承载力,也对合理预测钢管混凝土框架结构的屈服机制造成一定困难。

基于有限元软件ABAQUS建立了钢管混凝土柱-钢梁环板节点的三维有限元数值模拟模型,并用已有试验结果校验了理论模型。通过对典型试件的受力特性进行分析,探讨了各主要参数对此类节点抗弯承载力的影响规律,并在数值回归的基础上建议了此类节点抗弯承载力的简化计算公式。

1 节点有限元数值模型

1.1 有限元模型的建立

所研究的节点试件中,钢梁及钢管满足ABAQUS中的弹塑性材料本构模型,钢材满足Von-M ises屈服准则和相关流动法则。其中低碳软钢的应力-应变关系采用二次塑流模型,高强钢材的应力-应变关系采用线性强化模型,其应力-应变关系表达式可参考文献[1]。

钢管中核心混凝土采用ABAQUS中的塑性损伤模型[13],该模型基于非相关流动法则。其单轴受压应力-应变关系采用韩林海等[1]给出的相应表达式如下：

式中：x=ε/ε0,y=σ/σ0,ε和 σ分别为混凝土受压应变和应力,ε0和σ0分别为混凝土受压时峰值应变和峰值应力,其余参数含义及表达式可参见文献[1]。该模型可合理地反映钢管对核心混凝土的被动约束作用,已成功应用于钢管混凝土结构的大量理论模拟中。

混凝土受拉软化性能基于能量破坏准则[1],通过断裂能与应变的关系表达式实现,其中混凝土受拉峰值应力为 σp=0.26(1.25 f′c)2/3,其中 f′c为混凝土圆柱体抗压强度,单位为N/mm2。

合理的单元类型是准确模拟的关键。建模时钢管和钢梁采用四节点完全积分格式的壳单元,厚度方向采用9点Sim pson积分以满足一定的计算精度。核心混凝土采用八节点三维实体单元。网格划分时进行网格试验对比,在保证计算精度要求的前提下选择1个合理的网格划分密度,以寻求计算精度和效率之间的合理匹配。

钢管混凝土柱建模时需考虑钢管与混凝土之间的相互作用,建模时通过接触模型来实现,两者界面法向定义为硬接触,切向考虑粘结滑移,且切向力模拟采用库仑摩擦模型[1]。

边界条件的施加应尽可能模拟试验的支座条件,故在钢管混凝土柱底部的端板底面中线上,约束其3个方向的平动自由度,以模拟柱底部的平面铰支座边界。在柱顶端施加 y方向的平面外平动约束,在梁端约束竖向和平面外方向线位移,放松x方向的位移[14]。节点典型的有限元模型网格划分及边界条件如图1所示。

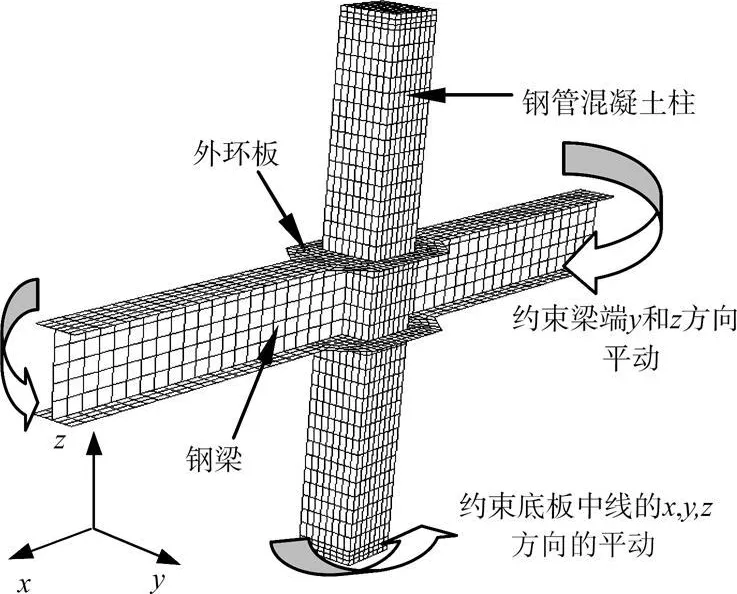
图1 典型节点有限元模型及边界条件

加载时,先在柱顶施加轴力,当施加至预定轴力稳定后,对于柱端加载节点试件,在柱端一侧施加水平方向的荷载或位移;对于梁端加载试件,在梁端施加竖向荷载或位移。文中非线性方程采用New ton-Raphson迭代方法求解,以获取其荷载-位移全过程曲线。

1.2 有限元模型的验证

文献[14]中进行了大量钢管混凝土柱-钢梁环板节点试件的算例对比,表明有限元计算结果与有关研究者完成的环板节点试验值总体吻合良好,验证了本文有限元模型及材料模型等的正确性。图2给出了采用本数值模拟模型计算得到的文献[10]-[12]中部分环板节点试验试件分别在柱端加载和梁端加载情况下的数值计算荷载-位移曲线与试验结果的比较,可见总体上二者吻合良好。图2(a)中试件SJ-21理论计算曲线的后期没有下降,主要原因是数值模型中没有考虑钢梁的初始缺陷且钢材材性为二次塑流模型,因此理论计算中钢材在后期处于强化阶段,从而造成其后期承载力一直上升,而试验中加载后期由于钢梁会出现局部屈曲,其后期承载力会下降。

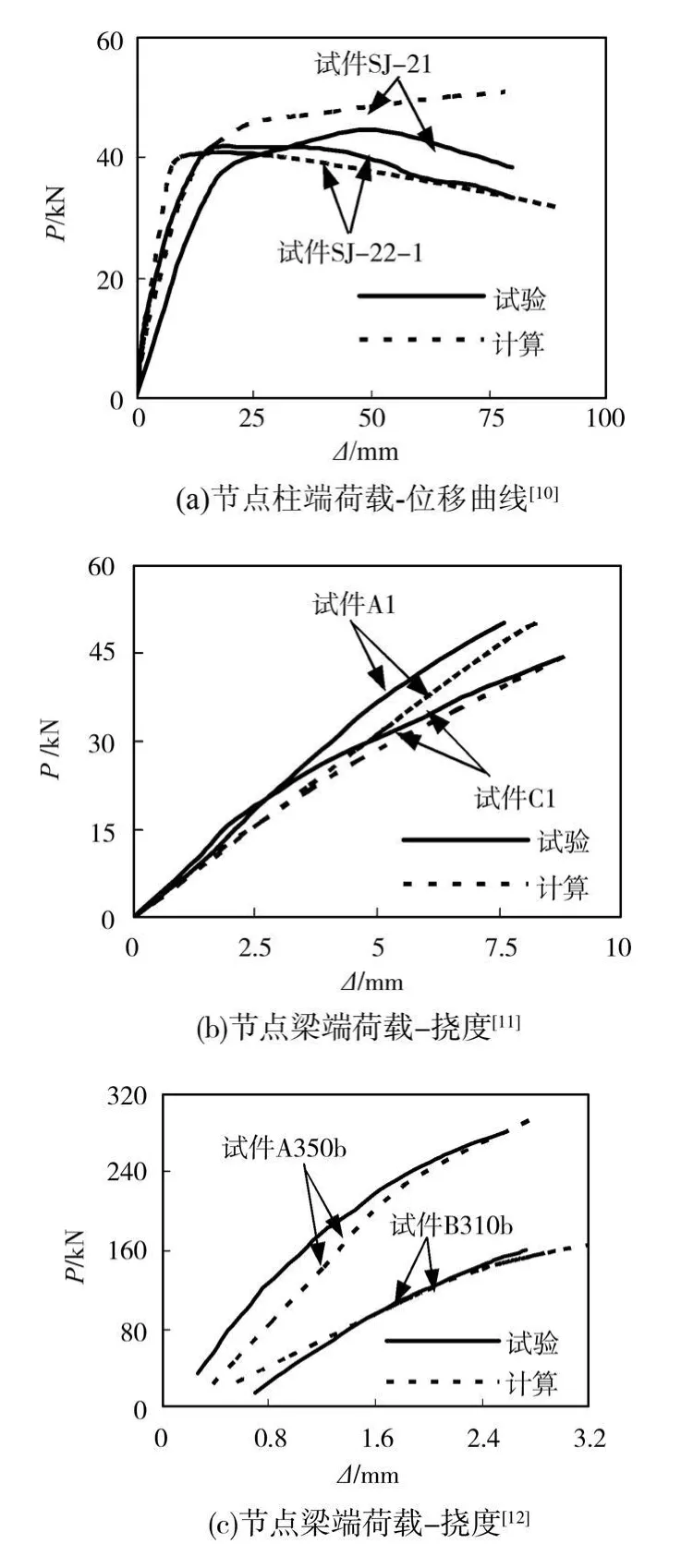
图2 试验值与有限元计算值比较

1.3 节点受力及破坏特性分析

王文达等[10]进行了方钢管混凝土柱-钢梁环板式节点的滞回性能试验研究,考察了不同环板宽度和柱轴压比的节点试件的力学性能和破坏特点,试验结果表明,该文中节点的最终破坏模式分别为梁端塑性铰破坏或环板破坏(环板尺寸最小的试件),节点核心区并未出现破坏,可见该类节点的节点域的抗弯及抗剪承载力均能满足要求。

选取文[10]中SJ-21和SJ-23-2试件试验后的破坏模式进行对比分析。图3所示的照片为试验结束后剖开节点域钢管后混凝土的状态,可见节点域混凝土并未出现裂缝,节点域混凝土具有足够的抗弯及抗剪承载力。

图3 典型节点的节点域混凝土状态对比

为进一步了解图3所示节点试件在受力全过程中节点域混凝土的受力特性,利用前述有限元模型分别对这2个节点试件进行了数值模拟,并进行了微观受力特性分析,理论计算得到的试件达到极限承载力时节点域混凝土应力状态也一并在图3中给出。由图3节点域混凝土的应力云图可见,核心区混凝土的应力数值较小,小于其混凝土的极限抗拉强度,故混凝土并未出现裂缝和破坏,这和试验现象一致。可见,文献[10]中的节点试件在发生破坏时,核心区抗弯及抗剪承载力满足要求,节点核心区不会出现破坏。

2 各参数对节点抗弯承载力的影响

尽管文献[10]中完成的节点试验表明,按照目前规范设计的此类节点其核心区并未出现破坏,但为了获取此类节点的抗弯承载力,应提供其设计公式以供验算。为获得环板式节点抗弯承载力的计算方法,首先需要对影响节点抗弯承载力的主要因素进行参数分析,获得各主要参数对节点抗弯承载力的影响规律,并进一步进行参数分析,最终提供其设计公式。

首先对柱端施加水平荷载的节点进行研究,即选取有侧移框架的中节点进行分析,且要求其破坏模式为梁破坏,即为强柱弱梁节点。参数分析时,节点的极限抗弯承载力暂取节点水平极限荷载P max对应的节点弯矩,而节点的初始刚度则参考韩林海等[1]暂取节点弯矩-转角关系曲线中0.2 Mu,j所对应的割线刚度。定义节点转角为节点屈服前后梁柱的夹角变化,具体确定方法同文献[1]。

影响钢管混凝土柱-钢梁环板节点弯矩-转角关系曲线的因素可能有：环板宽度、钢梁极限弯矩、柱截面含钢率、钢管强度、钢梁钢材强度、核心混凝土强度、轴压比、梁柱线刚度比等。参数分析时选用的典型构件基本信息如下：钢管混凝土柱截面D(B)×t=400×9.3mm,含钢率α=0.1(含钢率定义为α=A s/A c,其中 A s和分别为钢管和核心混凝土面积)。Q345钢材,C60混凝土,柱高 H=3.3m;钢梁采用Q345钢材,截面 H400×200×8×10 mm,跨度L=6.6 m。轴压比取0.4(轴压比暂定义为n=N0/N u,N0为柱顶轴力,N u为柱轴压承载力,由DBJ13-51-2003[3]确定)。

分析结果表明,圆、方钢管混凝土柱-环板节点的弯矩-转角关系曲线变化规律基本相似,下面只给出方钢管混凝土柱-环板节点的参数分析结果。

2.1 环板宽度的影响

图4(a)给出了不同环板宽度b时的环板节点弯矩-转角(M-θ)关系曲线。分析时环板宽度从60mm到180 mm变化。由图可见：随着环板宽度增大,节点抗弯承载力增大,但当环板宽度增大到一定程度后抗弯承载力增加的幅度趋于缓慢,而初始刚度总体上随环板宽度的增大变化并不显著。

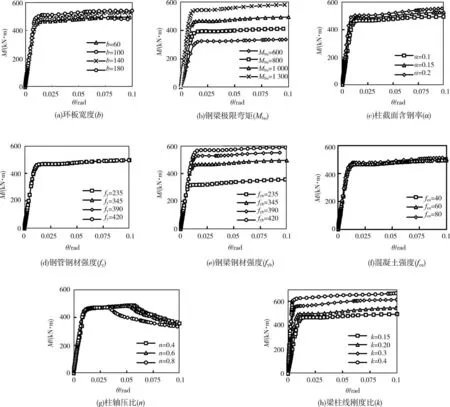
图4 各主要参数对方钢管混凝土柱-环板节点弯矩-转角(M-θ)关系的影响

2.2 钢梁极限弯矩

图4(b)给出了不同钢梁极限弯矩M bu时的节点弯矩-转角(M-θ)关系曲线,其中钢梁极限弯矩单位为kN◦m。由图可见,随着钢梁极限弯矩的增大,节点的承载力和初始刚度均有明显的增大趋势。需要注意的是,在对钢梁极限弯矩变化中,试件仍满足“强柱弱梁”要求。

2.3 柱截面含钢率

图4(c)给出了不同含钢率α时的节点弯矩-转角(M-θ)关系曲线。由图可见,总体上柱截面含钢率对节点的抗弯承载力和初始刚度有一定影响,随着柱截面含钢率的增大,节点抗弯承载力和初始刚度相应增大。

2.4 钢管强度

图4(d)给出了不同钢管强度下的节点弯矩-转角(M-θ)关系曲线。可见钢管强度对节点弯矩-转角关系影响不大,随着钢管强度的增大,节点抗弯承载力和节点初始刚度增大趋势不明显。钢管强度之所以对节点弯矩-转角关系影响不大,主要是由于该文分析的是强柱弱梁节点,节点的抗弯承载力主要是由钢梁控制。

2.5 钢梁强度

图4(e)给出了钢梁强度不同时的节点弯矩-转角(M-θ)关系曲线。可见钢梁强度对节点弯矩-转角关系有显著影响,随着钢梁强度的增大,节点抗弯承载力有明显增大,但对节点初始刚度影响不明显,主要原因是钢梁材料强度增加对其刚度并无影响。

2.6 混凝土强度

图4(f)给出了在不同混凝土强度时的节点弯矩-转角(M-θ)关系曲线。可见随着柱核心混凝土强度的提高对节点抗弯承载力和初始刚度的影响并不明显。

2.7 柱轴压比

图4(g)给出了不同柱轴压比时节点弯矩-转角(M-θ)关系曲线,分析时暂取轴压比从0.4到0.8变化。可见,改变轴压比对节点的抗弯承载力影响较小,但随着轴压比的增大,节点承载力的下降段出现的越早,节点延性下降。节点初始刚度随轴压比的增大变化也不明显。

2.8 梁柱线刚度比

图4(h)给出了不同梁柱线刚度比时的节点弯矩-转角(M-θ)关系曲线,分析时梁柱线刚度比从0.15至0.4变化。可见随着梁柱线刚度比的增大,节点的抗弯承载力和初始刚度都有明显提高。

3 节点抗弯承载力计算探讨

通过上述的参数分析结果可见,对于所研究的有侧移的钢管混凝土柱-钢梁环板节点,影响其抗弯承载力的主要因素有：环板宽度、钢梁极限弯矩、柱截面含钢率、钢梁钢材强度、梁柱线刚度比。根据以上参数分析结果,对节点抗弯承载力M jy进行回归分析,可得到此类节点的抗弯承载力计算公式如下：

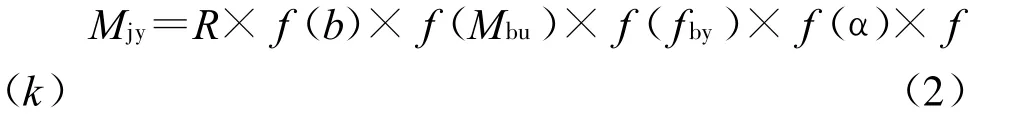
式中：R为系数,对于圆形柱-钢梁节点为7.12×10-5,方形柱-钢梁节点为 5.37×10-5,f(b)、f(Mbu)、f(fby)、f(α)、f(k)分别为 Mjy与环板宽度 b、钢梁塑性弯矩M bu、钢梁强度 f by、柱截面含钢率α、梁柱线刚度比k的关系表达式。

公式(2)中的各参数表达式,对于方钢管混凝土柱-钢梁节点如下：

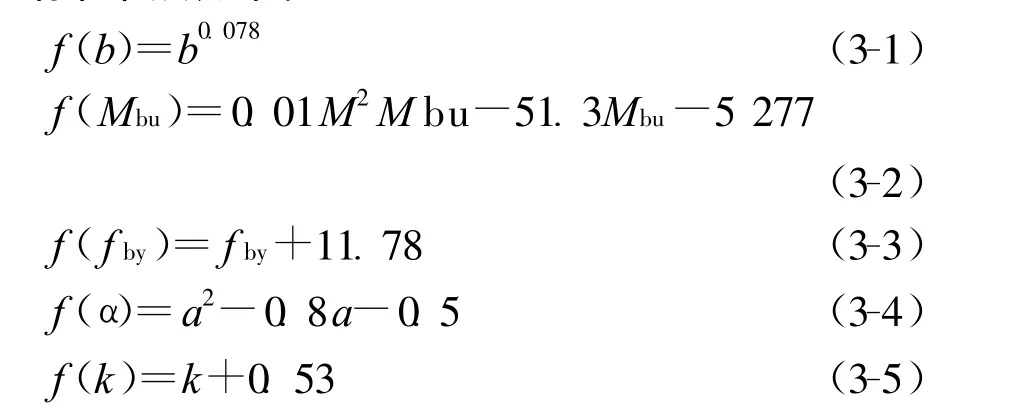
对于圆钢管混凝土柱-钢梁节点如下：

为验证该文建议公式的准确性,对节点抗弯承载力的简化计算值与有限元计算值及有关试验结果进行了比较,部分结果如图 5所示,其中和分别为按本文简化公式(2)计算和有限元计算的数值。为便于和M u,cal结果比较,文献[10]中的节点试验结果也列于图5中,其数值列于横轴数值(即Mu,FEM)中。可见总体上简化公式和有限元计算结果吻合良好,且与试验结果也具有良好的一致性,表明该文提出的节点抗弯承载力的简化计算公式有较好的精确性。

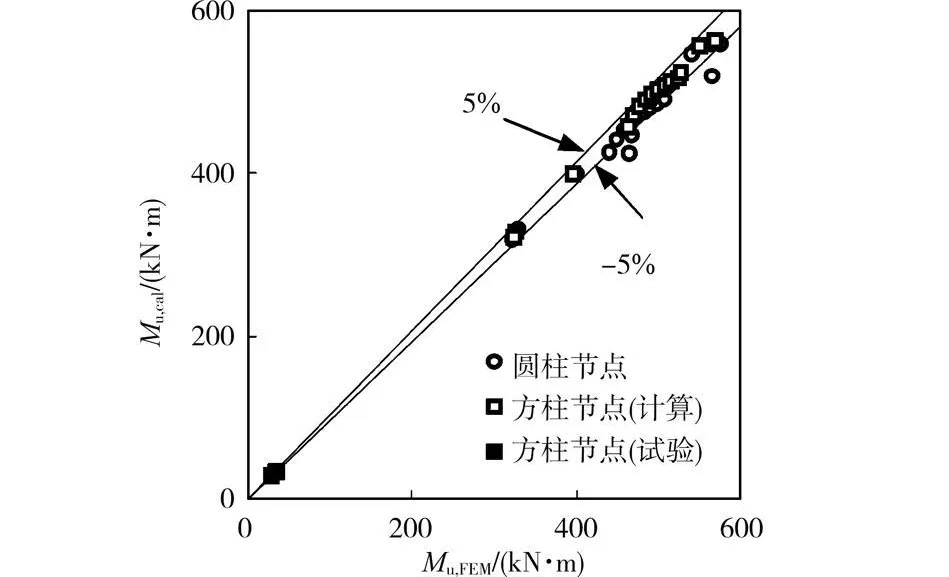
图5 节点抗弯承载力的简化计算与有限元计算及试验结果比较

4 结论

基于该文的研究,有以下初步的结论：

1)ABAQUS软件可较好地模拟钢管混凝土柱-钢梁加强环板节点的力学性能,理论结果与试验值吻合良好。

2)对于该文所研究的环板式节点,环板宽度、钢梁极限弯矩、柱截面含钢率、钢梁强度、梁柱线刚度比是影响节点抗弯承载力的主要因素。

3)通过数值回归建议了有侧移框架中的钢管混凝土柱-钢梁外加强环板节点的抗弯承载力简化计算公式,简化公式结果与有限元计算结果吻合良好。

[1]韩林海,陶忠,王文达.现代组合结构和混合结构-试验、理论和方法[M].北京：科学出版社,2009.

[2]CECS 159：2004.矩形钢管混凝土结构技术规程[S].北京：中国计划出版社,2004.

[3]DBJ 13-51-2003.钢管混凝土结构技术规程[S].福州,2003.

[4]THOMANN M ICHEL,LEBET JEAN-PAUL.A mechanical model for connections by adherence for steel-concrete composite beams[J].Engineering Structures,2008,30(1)：163-173.

[5]SH IN KYUNG-JAE,K IM YOUNG-JU,OH YOUNGSUK.Seism ic behaviour of composite concrete-filled tube column-to-beam moment connections[J].Journa l of Constructional Stee l Research,2008,64(1)：118-127.

[6]CHENG CH IN-TUNG,CHAN CH EN-FU,CHUNG LAP-LOI.Seismic behavior of steel beams and CFT column moment-resisting connec tions w ith floor slabs[J].Journa l of Constructional Steel Research,2007,63(11)：1479-1493.

[7]LI X,XIAO Y,WU Y T.Seism ic behavior o f exterior connections w ith steel beams bo lted to CFT columns[J].Journal of Constructional Steel Research,2009,65(7)：1438-1446.

[8]CHOI SUNG-MO,LEE SEONG-HUI,HONG SUNGDUK,et al.Structural capacities of tension side for CFT square column-to-beam connec tionswith combined-cross diaph ragm[J].Advances in Structural Engineering,2008,11(2)：209-227.

[9]WANG WEN-DA,HAN LIN-HA I,UY BRIAN.Experimental behavior of steel reduced beam section(RBS)to concrete-filled CHS co lumn connections[J].Journalof Constructional Steel Research,2008,64(5)：493-504.

[10]王文达,韩林海,游经团.方钢管混凝土柱-钢梁外加强环节点滞回性能的实验研究[J].土木工程学报,2006,39(9)：17-25.WANG W EN-DA,HAN LIN-HA I,YOU JING-TUAN.Experimental studies on hysteretic behavior s of steel beam to conc rete-filled SHS colum n connections with stiffening ring[J].China Civil Engineering Journal,2006,39(9)：17-25.

[11]陈娟,王湛,袁继雄.加强环式钢管混凝土柱-钢梁节点的刚性研究[J].建筑结构学报,2004,25(4)：43-54.CHEN JUAN,WANG ZHAN,YAUN JI-XIONG.Research on the stiffness of concrete-filled steel tubu lar column and steelbeam joint with stiffening ring[J].Journal of Building Structures,2004,25(4)：43-54.

[12]李成玉,郭耀杰,李美东.钢管混凝土结构外加强环式节点刚性试验研究[J].工业建筑,2006,36(9)：81-83.LICHENG-YU,GUO YAO-JIE,LIMEI-DONG.Experimental research on the joint stiffness of CFT-steel beam space joint with outer concentric annular-stiffer[J].Industrial Construction,2006,36(9)：81-83.

[13]LUBLINER J,OLIVER J,OLLERSO,et al.A plasticdamagemodel for concrete[J].International Journal o f Solids and Structures,1989,25(3)：299-326.

[14]秦庚.钢管混凝土柱-钢梁环板节点力学性能与设计方法研究[D].兰州：兰州理工大学,2009.