高频循环剪切下结构与松砂接触面的土体特性

陈福全,韩 钧

(福州大学土木工程学院,福州350108)

砂性土的结构可视为一个由单粒、集粒或凝块等骨架单元共同形成的空间结构体系。现在对砂性土这种散粒性材料的研究多使用连续介质中的各种理论,然而这种理论对砂性土的性质、形状、大小等特殊性考虑不足,细观结构的复杂性决定了砂性土具有复杂的工程力学性质。该文针对连续介质中各种理论的不足,引进颗粒离散元理论来模拟颗粒介质的运动及相互作用,它克服了传统连续介质力学模型的宏观连续性假设,可以从细观角度对土的工程特性进行数值模拟,并通过颗粒结构的细观参数的研究来分析材料的宏观力学行为。

在研究砂土的力学性质过程中,砂土的密实度对土的工程性质有重要影响。通常情况下用相对密实度D r来反映砂土的密实度,中国学者收集了大量砂土资料,建立了砂土相对密实度D r与天然孔隙比e的关系,得出了直接按天然孔隙比e确定砂土密实度的标准,论文以此作为松砂的定义进行研究[1]。

近年来,已有一些学者在试验、理论和数值模拟等方面对土与结构接触面的力学特性及其对桩土相互作用的影响进行了较深入的研究[2-6],包括砂土或黏性土与结构接触面特性试验研究[7-9]。考虑到试验很难对此进行深入研究,而且已有相关的文献极少涉及高频反复剪切问题。本文采用PFC3D4.0软件,应用颗粒离散元分析方法对松砂与结构接触面在高频率反复剪切荷载作用下的特性进行研究。这对于研究高频振动打桩过程中,板桩对桩周砂土反复剪切时对砂土力学性能的影响,以及砂性土深层竖向高频振动致密时振杆与砂土的高频反复前切特性具有一定的理论意义。这里的高频是指在相对于一般动力打桩的振动频率而言,在10 Hz以上。

1 颗粒离散元分析的试样制备

物理模型如图1,是在Nicolas M[2]等人的物理模型基础上改进的,图2是在物理模型的基础上用颗粒离散元法来建立数值模型,由高频反复剪切板按一定的位移幅度及频率进行单向往返反复剪切,一定厚度外边界施加围压p,上面边界板右侧由铰结点约束。颗粒离散元分析模型如下所述。

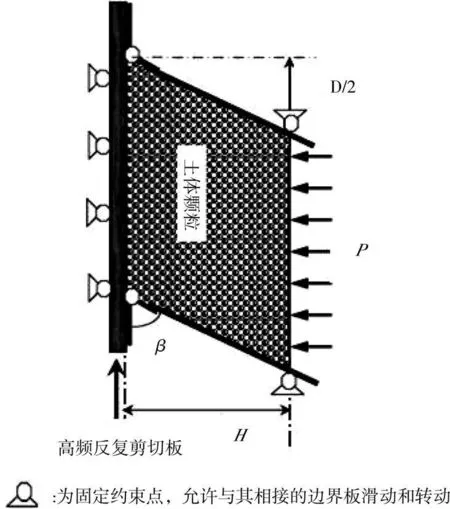
图1 物理模型示意图

1.1 砂箱模型的建立

在PFC3D模拟中建立一个由6面无限刚性墙来确定砂箱的尺寸大小。其中砂箱尺寸为宽20 mm,厚0.8mm,高50mm,粒子生成器根据孔隙率的大小来随机生成颗粒数目,在图2中,按照松砂孔隙率来随机生成颗粒半径大小为0.3～0.4 mm的颗粒,文中只考虑粒子半径按一定范围均匀分布,为1.33,在颗粒生成过程中采用了颗粒放大系数,取值1.5,以获得更好的密实度。周健[11]模拟砂土双轴试验时,对比研究改变颗粒直径对试验曲线的强度、模量的影响范围,发现颗粒大小对数值试样的宏观特性有一定的敏感性,但是通过选择合适的颗粒粒径之比可以消除这种敏感性,并认为对于土体这种复杂的材料,采用非常精确的数值进行模拟是没有必要的,能够保证模拟的结果在工程误差允许的范围内即可。

图2 数值模型示意图

用无限刚性墙作为边界条件的模型通过循环消除试样内部初始成样产生的局部不均衡力。然后删除左右、上下4面墙,最左边由颗粒半径为0.4mm的69个颗粒串连在一起模拟板桩,上、下2面墙分别由颗粒半径为0.4 mm的33个颗粒串连在一起模拟颗粒墙,其中将板桩与上下2面墙组成的颗粒平行粘结连在一起,使得板桩在竖向高频反复剪切过程中带动上下2面颗粒墙运动。最右边由颗粒半径为0.4 mm的62个颗粒串连在一起模拟颗粒墙。固定这些构成边界条件的颗粒,记录作用在这些边界颗粒上的静应力,在这些固定的边界球重新释放后,将记录的静应力施加到相应的边界颗粒上作为基本作用力,使其达到初始静力平衡状态。

板桩和颗粒墙的生成。删除左右、上下4面无限刚性墙,最左边由一排颗粒串模拟板桩,上下各由颗粒串模拟颗粒墙,板桩与上下两面颗粒墙进行平行粘结。最右边由一排颗粒串模拟颗粒墙(根据模型的需要,此柔性墙组成的颗粒之间不会产生相对的转动)。用FISH语言开发模拟的柔性墙由颗粒组成,颗粒与颗粒之间可以承受一定的拉力和变形。上下2面墙的一侧各由2个球来设置约束点,使得上下墙与这2个球之间只能发生相对的滑动和转动。

赋予板桩和颗粒墙材料性质和力学特性,设置组成板桩颗粒的摩擦系数、颗粒刚度及组成颗粒墙颗粒的摩擦系数和颗粒刚度,还需设置板桩与颗粒墙之间的平行粘结刚度和强度。

当板桩在高频反复剪切过程中产生波的传播,若右边的颗粒墙用刚性墙,模型受波反射的影响,故模拟过程中用颗粒墙来代替。对于右边的颗粒墙来说,本身就在其上面施加了一个围压,那么松砂在剪缩过程中一方面由于板桩的剪切使得颗粒致密,另一方面边界围压也对整个砂箱模型起到致密作用。因此对右边的颗粒墙,在其上检测的速度并不是单纯的反射波提供的速度,而要加上围压对颗粒墙提供的速度。为解决这问题,先不施加边界围压,板桩剪切1个循环来检测右边颗粒墙的速度,然后在颗粒边界接触处的法向方向和切向方向分别累加法向应力和切向应力将法向应力yn和切向应力检测出来,根据Kamp[12]分别采用下面2式进行计算,然后施加边界围压,那么右边颗粒墙上施加的力包括静应力、法向应力切向应力和边界围压产生的力。

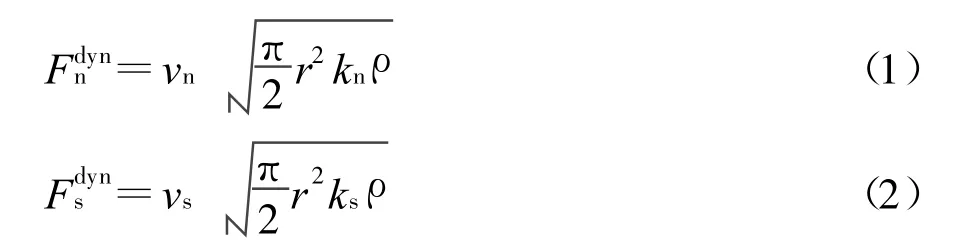
1.2 参数的标定

颗粒流PFC3D的颗粒DEM模型的物理力学参数一般是不能简单地与颗粒细观的一系列的结构参数联系,这和我们以往熟悉的连续类型的模型是有本质的差别。对于颗粒离散元模型,物理力学特性受被颗粒的尺寸和组装方式影响复杂多变。

对于砂性土来说,反应材料宏观的力学参数包括变形模量E C、等效内摩擦角φ、峰值强度σf等。反应材料细观参数包括颗粒摩擦系数μ、颗粒法向接触刚度k n、颗粒切向接触刚度k s、颗粒法向接触刚度与颗粒切向接触刚度比值kn/ks、颗粒密度ρ、颗粒平行粘结的法向接触刚度¯k n、颗粒平行粘结的切向接触刚度¯ks、颗粒平行粘结的法向接触刚度与切向接触刚度比值¯k n/¯k s、平行粘结的半径乘子系数λ等。对砂性土,罗勇[13]进行了大量的数值试验前提和一些合理的假设条件下,可以通过颗粒摩擦系数来标定颗粒的内摩擦角,通过选择颗粒的法向接触刚度和切向接触刚度来标定材料的变形模量。

1.3 参数的设置

通过反复比较已有文献参数的设置,来选择模拟过程中参数的设置,主要分析颗粒半径的设置(最小颗粒半径、最大颗粒半径、颗粒放大系数)和颗粒刚度的设置(颗粒法向接触刚度、颗粒切向接触刚度、颗粒法向接触刚度和颗粒切向接触刚度的比值),具体表格见文献[14-17]。针对这些文献,本文对PFC模型中参数的设置如表1。

表1 松砂细观参数

1.4 围压和剪切荷载的施加

1.4.1 围压的施加 对试样模型右侧的颗粒墙施加边界围压,颗粒墙由具有一定连接强度的颗粒组成,当最左边的板桩进行竖向高频反复剪切时,对松砂来说颗粒之间孔隙较大,颗粒之间发生相互错动引起整个土样的密实,在边界围压的作用下,使得颗粒墙向板桩方向移动。组成右边颗粒墙的颗粒只能发生平动,颗粒之间不能发生旋转,可以承受一定的拉力和变形,围压根据试样的高度和组成墙体的颗粒个数换算成力施加到右边颗粒墙的每个颗粒上,在试样过程中也保证了围压的稳定。曾远[20]对砂土的室内双轴试样数值模拟过程中,对边界条件的模拟利用FISH语言开发模拟柔性边界,使左右边界条件采用具有一定连接强度的颗粒组成柔性边界,比刚度较大的墙体有更好的模拟性。

1.4.2 反复剪切荷载的施加 对左边的板桩施加一个竖向高频反复剪切荷载,板桩由半径为0.4mm的颗粒连接而成,这样跟砂土相剪切的那部分板桩颗粒大小与砂土颗粒大小非常接近,避免了砂土颗粒进入组成板桩颗粒的孔隙中而引起很大的拉应力。

模拟的板桩颗粒通过施加速度来实现反复剪切荷载,由于组成板桩的颗粒与组成上下两面颗粒墙的颗粒进行了平行粘结,所以当板桩在剪切时,能带动上下2面墙的运动,从而能使砂箱模型中颗粒之间发生错动而填满空隙。板桩反复剪切的实现是通过调用一个专门编写子程序函数来实现的,这个子程序函数仅实现在Z方向的单向振动,而在X方向和Y方向速度设为零,具体的数学表达式如下：

表2 桩结构细观参数

2 数值模拟结果分析

在PFC3D模拟试验过程中,通过计算机屏幕可以直接实时观察和记录板桩对松砂在高频反复剪切下的细观响应。在高频反复剪切过程中可以检测砂箱中孔隙率和体应变的变化情况。

2.1 颗粒摩擦系数的影响

模型中球颗粒采用了纯圆的球颗粒,这与实际砂土具有棱角的性质不同,要想模拟砂土这种以摩擦特性为主的材料就必须通过研究颗粒接触之间的摩擦系数的影响。板桩在频率为15 H z,振幅为0.2mm的高频反复剪切作用下剪切砂土,当反复剪切1 000个循环时,整个接确面土体中孔隙率的变化波动非常的小,近似认为整个砂箱孔隙率的变化趋于稳定。松砂的初始孔隙率为0.4,通过分析砂土颗粒摩擦系数为 0.2、0.3、0.4、0.5来研究在高频反复剪切过程中对砂箱孔隙率和体应变的影响。图3反映循环后砂箱的孔隙率值,图4反映了循环后接触面土体的体应变。

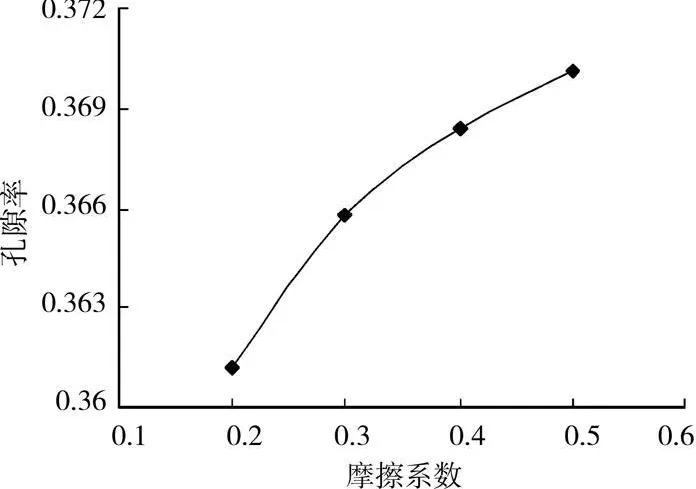
图3 颗粒摩擦系数对孔隙率的影响

图4 颗粒摩擦系数对体应变的影响

从图中可看出随着颗粒摩擦系数的提高,孔隙率和体应变降低的越少,表明接触面松砂的剪缩效果越不明显。这主要是因为桩结构在高频反复剪切过程中会使松砂颗粒之间会发生相互的错动,对于松砂而言,要产生相对错动就只需挤密周围的孔隙就可以,不用上下翻越,一旦颗粒的摩擦系数越大,那么颗粒之间错动就需要克服更大的力,那么相对摩擦系数小的颗粒,其挤密的效果就越不明显,使得松砂剪缩性不明显。

2.2 颗粒刚度的影响

在颗粒刚度比k n/k s不变的情况下,通过改变颗粒最大法向刚度来检测松砂在高频反复剪切过程中力学性状的变化。板桩在剪切频率同样为15 Hz,剪切振幅为0.2mm,边界围压为 100 kPa,砂箱中初始孔隙率为0.4的情况下,来考虑颗粒最大法向刚度为 800 kPa 、900 kPa、1 000 kPa 、1 100 kPa下孔隙率、体应变的变化情况,图5反映循环后砂箱的孔隙率值,图6反映循环后砂箱的体应变。

图5 颗粒刚度对孔隙率的影响

图6 颗粒刚度对体应变的影响

分析表明,接触面松砂颗粒刚度越小,其剪缩性越好。这主要是因为土体由破碎的固体颗粒组成,土的宏观变形由颗粒本身变形和颗粒间位置的变化两部分所引起。颗粒刚度越大,导致变形主要是颗粒位置的改变引起;颗粒刚度小,导致变形可以由颗粒自身形变和位置变化同时引起。所以当颗粒刚度越小时,颗粒之间不仅有位置的变化,还有自身形变,所以颗粒之间更容易挤密,从而表现出孔隙率下降的更快,剪缩性越好。曾远[15]在对砂土的细观参数对宏观特性的影响进行研究时得出结论：颗粒刚度越小,其剪缩性越好,结论相似,但本文是针对高频反复剪切的情况。

2.3 颗粒刚度比的影响

在板桩剪切频率为15 Hz,剪切振幅为0.2mm的情况下,颗粒法向刚度1 000 kPa不变。改变颗粒的切向刚度,分析颗粒法向刚度与切向刚度比值在4、3、2、1这4种情况下孔隙率、体应变的变化规律,图7反映循环后砂箱的孔隙率值,图8反映循环后接触面土体的体应变。

图7 颗粒刚度比对孔隙率的影响

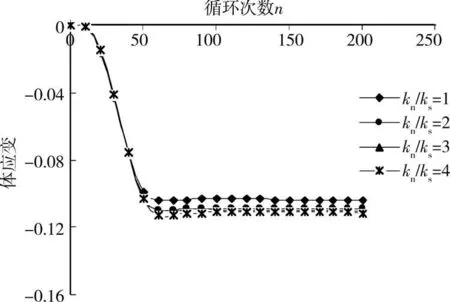
图8 颗粒刚度比对体应变的影响

随着颗粒刚度比的增加,孔隙率和体应变略有下降,但并不明显,可认为颗粒刚度比砂土的力学性质影响不明显。罗勇[14]对无粘性土工程力学性质三维颗粒元模拟过程中认为是不同的颗粒刚度比对砂土应力—应变变化关系和体积应变—轴应变的影响效果不是很明显。研究表明不同颗粒刚度比的松砂,在受到高频反复剪切过程中,其剪缩效应变化不明显。

2.4 边界围压的影响

对最右边的颗粒墙施加一个边界围压在分析中非常重要,显然,考虑越深的桩周土层,其侧向应力越大,反映到模型中边界围压越大。所以考虑边界围压对整个砂箱孔隙率、体应变的变化规律能反映在不同深度砂土土层的力学性能,图9反映循环后砂箱的孔隙率值,图10反映循环后接触面土体的体应变。

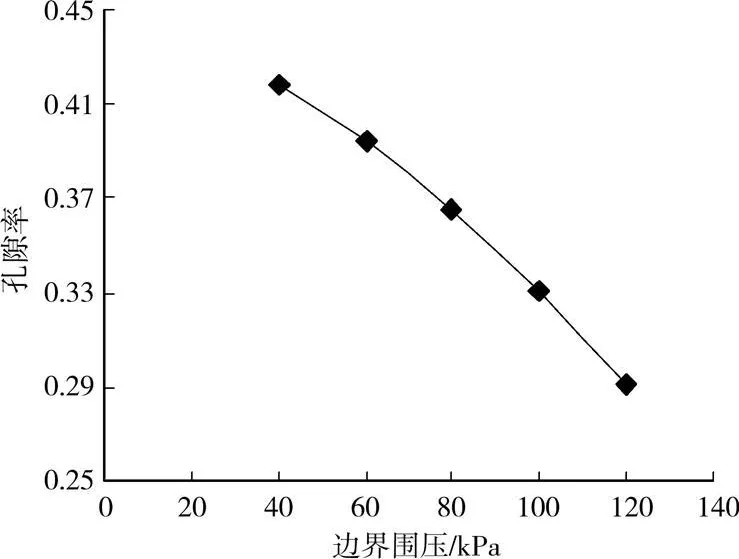
图9 边界围压对孔隙率的影响

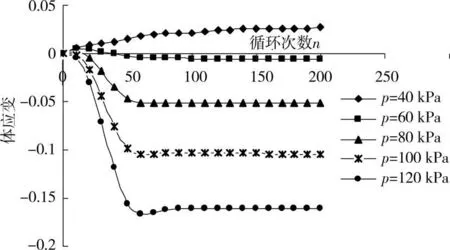
图10 边界围压对体应变的影响

随着边界围压的增加,松砂的剪缩效应更加明显。在边界围压很小的情况下如在40 kPa时,整个砂箱模型还有略微的剪胀,但是随着围压的增加,松砂呈现出剪缩的效果。这个模拟的结果反映到实际工程中可以说明,在打桩过程中,越是深层的桩周土,其孔隙率降低得越是明显。贾敏才[16-17]通过试验与离散元研究了砂土地基振冲加固机理,给出振冲后距振点0.25单位处孔隙率随深度变化曲线,表明在研究的深度范围内,土体孔隙率的降低幅度随着深度的增加而明显增大,与本文结论一致。

2.5 剪切振幅的影响

研究板桩在高频反复剪切过程中剪切振幅对松砂剪缩的影响,考虑剪切振幅分别在0.1 mm,0.2 mm,0.4mm,0.5mm这4种情况下对整个砂箱孔隙率、体应变的影响,图11反映循环后砂箱中的孔隙率值,图12反映循环后土体的体应变。

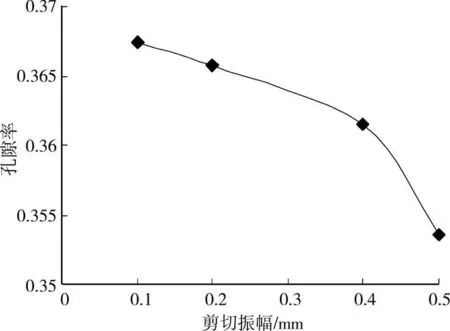
图11 剪切振幅对孔隙率的影响

图12 剪切振幅对体应变的影响

分析表明剪切振幅越大,剪切得到的孔隙率、体应变越低,剪缩越明显。剪切振幅较大时一方面在剪切过称中板桩对桩周土体传递的能量越大,另一方面是板桩在剪切过程中带动上下2面颗粒墙,在大剪切振幅下,上下2面颗粒墙对砂箱颗粒的错动挤密效果就更加明显,所以使得大剪切振幅比小剪切振幅对整个砂箱的剪缩效果更好。M.Nicolas等[10]研究了循环剪切下颗粒的压缩,对砂箱模型施加一个水平向的反复循环剪切,结论与本文一致。

2.6 剪切频率的影响

板桩剪切振幅为0.1 mm,剪切频率分别为10 H z、15 H z、20 H z、25 H z,检测在不同的剪切频率下前100 s内孔隙率、体应变的变化情况,并分析剪切频率为10 H z和剪切频率为25 H z这2种情况下典型位置处砂土颗粒的运动轨迹。图13反映循环后砂箱的孔隙率值,图14反映循环后砂箱的体应变。图15、16显示在不同剪切频率下接触面土体典型位置处颗粒的运动情况。

图13和14反映的规律表明,在频率10～25 H z范围内,剪切频率越大,松砂压缩性越明显。图15和16典型位置颗粒的运动位移变化表明,相对初始颗粒位置,颗粒有向板桩移动的趋向,说明了颗粒之间错动压密的趋势,另一方面从板桩附近颗粒的位移变化看出离板桩越近的颗粒,受到板桩对其的剪切作用越明显。

图13 剪切频率对孔隙率的影响

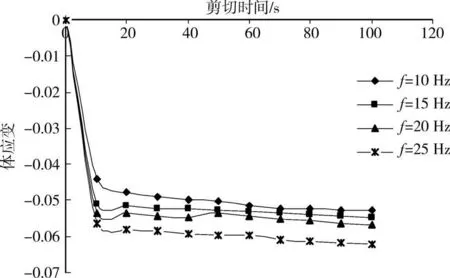
图14 剪切频率对体应变的影响

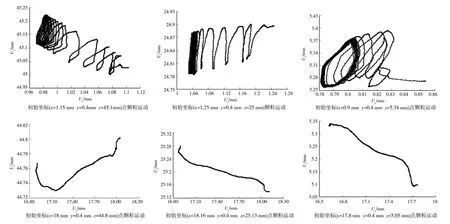
图15 典型位置处颗粒的运动位移(f=10 Hz)

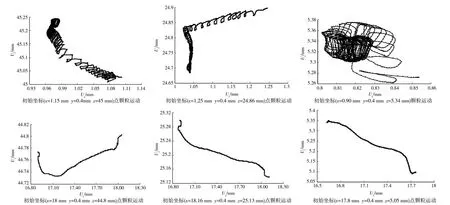
图16 典型位置处颗粒的运动位移(f=25 Hz)

3 结论

通过应用和开发颗粒离散元分析技术,研究高频反复剪切荷载下松砂与结构接触面土体响应的特性,通过对砂箱孔隙率和体应变的变化来反映松砂剪缩效应的影响因素,基本结论为：

1)松砂颗粒摩擦系数和颗粒刚度越高,接触面的松砂的剪缩性越不明显。

2)松砂颗粒刚度比对松砂的剪缩性影响不明显,认为颗粒刚度比对砂土的力学性状影响较小。

3)边界围压、剪切振幅、剪切频率越高,松砂的剪缩性越明显。

4)仅对高频反复剪切作用下结构与接触土体性状进行了分析,但相应的接触面土体应力应变本构理论及其接触面本构模型有待于深入的研究。

[1]张克恭,刘松玉.土力学[M].北京：中国建筑工业出版社,2001.

[2]REDDY E S,CHAPMAN D N,SASTRY V V R N.Direct shear interface test for shaft capacity of piles in sand[J].Geotechnical Testing Journal,2000,23(2)：199-205.

[3]段文峰,廖雄华,金菊顺,等.桩-土界面的数值模拟与单桩Q-S曲线的数值分析[J].哈尔滨建筑大学学报,2001,34(5)：34-38.DUAN WEN-FENG,LIAO XIONG-HUA,JIN JUSHUN,et al.Numericalmodeling of pile-soil interface and numerical analysis of single pile Q-S curve[J].Journal of Harbin University of Civil Engineering and A rchitecture,2001,34(5)：34-38.

[4]DESA ICS,DRUM M E C.Cyclic testing and modeling of interfaces[J].Journal of Geotechnical Engineering,1985,111(6)：793-815.

[5]张嘎,张建民.粗粒土与结构接触面单调力学特性的试验研究[J].岩土工程学报,2004,26(1)：21-25.ZHANG GA,ZHANG JIAN-M IN.Experimental study on monotonic behavior of interface between soil and structure[J].Chinese Jounal of Geotechnical Engineering,2004,26(1)：21-25.

[6]张嘎,张建民.循环荷载作用下粗粒土与结构接触面变形特性的试验研究[J].岩土工程学报,2004,26(2)：254-258.ZHANG GA,ZHANG JIAN-M IN.Experimental study on cyclic behavior of interface between soil and structure[J].Chinese Jounal of Geotechnical Engineering,2004,26(2)：254-258.

[7]DESAICS,NAGARAJBK.Modeling for cyclic normal and shear behavior of interfaces[J].Journal of Geotechnical Engineering,1988,114(7)：1198-1217.

[8]FAKHARIN K,EVGIN E.Cyclic sim p le-shear behavior of sand-steel interfaces under constant normal stiffness condition[J].Journal of Geotechnical&Geoenvironmental Engineering,1997,123(12)：1096-1105.

[9]YOSH IM IY,K ISH IDA T.A ring torion apparatus for evaluation friction betw een soil and surface[J].Geotechnical Testing Journal,1981,4(4)：831-834.

[10]N ICOLASM,DURU P,POULIQUEN O.Com paction of a granular material under cyclic shear[J].The European Physical Journal E.,2000(3)：309-314.

[11]周健,池永.砂土力学性质的细观模拟[J].岩土力学,2003,24(6)：901-906.ZHOU JIAN,CH IYONG.Mesomechanical simulation of sandmechanical properties[J].Rock and SoilMechanics,2003,24(6)：901-906.

[12]KAMP T E,KONIEZKY L H,GUERIN F.Modeling of the Chagan underground nuclear test with the distinct element method[J].International Journal of Blasting and Fragmentation,1998(2)：295-312.

[13]罗勇.土工问题的颗粒流数值模拟及应用研究[D].杭州：浙江大学土木工程系,2007.

[14]周健,史旦达,贾敏才,等.砂土单调剪切力学性状的颗粒流模拟[J].同济大学学报：自然科学版,2007,10(35)：1299-1304.ZHOU JIAN,SH I DAN-DA,JIA M IN-CAI,et al.Numerical simulation ofmechanical response on sand under monotonic loading by particle flow code[J].Journal of Tong ji University：Natural Science,2007,10(35)：1299-1304.

[15]曾远,周健.砂土的细观参数对宏观特性的影响研究[J].地下空间与工程学报,2008,4(3)：499-503.ZENG YUAN,ZHOU JIAN.Influenceofmicro parameters of sandy soil on itsmacro properties[J].Chinese Journal of Underground Spaceand Engineering,2008,4(3)：499-503.

[16]贾敏才.砂土地基振冲加固的试验研究及颗粒流模拟[D].上海：同济大学,2003.

[17]贾敏才,王磊,周健.砂土振冲密实的细观颗粒流模拟[J].水利学报,2009,40(4)：421-429.JIA M IN-CA I,WANG LEI,ZHOU JIAN.M eso-mechanics simulation on vibrocompaction of sand with twodimensional particle flow code[J].Journal o f Hyd rau lic Engineering,2009,40(4)：421-429.