青藏线棚车在强横风下的倾覆稳定性

高广军，段丽丽，苗秀娟

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙，410075)

青藏铁路全长1 142 km，是世界上海拔最高、线路最长、气候最恶劣的高原铁路[1]。铁路沿线桥梁就有500多座，其中高于30 m的桥梁有7座，最高的是三岔河特大桥，仅墩高就有52.1 m。铁路顺山势而建，路堤较高，最高的路堤高大于25 m。青藏高原地区地势高亢开阔，又受到高空强劲西风动量下传的影响，成为全国风速和大风日数分布的高值区之一，沿线年平均大风日为115~160 d，最大风速为20~28 m/s[2]，历史上极端最大风速在 31 m/s 以上，安多地区高达38 m/s[3]。在强横风作用时，很容易引起列车脱轨或倾覆等事故[4-6]。历年来大风引起的事故均发生在高路堤或高架桥地段。而所有车辆中棚车的临界倾覆风速最低，临界倾覆风速仅为30 m/s[7-8]。在我国兰新线发生过的大风吹翻列车事故中，基本上都是空棚车，其倾覆形式包括车辆在轨道上的倾覆和车体在转向架上倾覆2种。为了预防事故的发生，很多研究人员研究了车辆在桥梁或路堤条件下的气动性能[9-11]，并建立了车辆在轨道上倾覆的数学模型[12-14]，甚至在线路上安装大风预警系统[15-17]。在青藏线也建立了一套大风预警与行车指挥系统，系统中包含有棚车在不同路段、不同风速下的车速限值。为此，本文作者采用棚车缩比模型的风洞试验的方法得到棚车的气动力系数，并同时建立车辆在轨道上倾覆和车体在转向架上倾覆的数学关系式，求出车辆运行车速和临界倾覆风速之间的关系。

1 棚车的缩比模型风洞试验

1.1 风洞试验条件

棚车风洞试验在中国空气动力研究与发展中心低速所的8 m×6 m 风洞进行。该风洞是1个开路式闭口串列双试验段大型低速风洞，试验在第2试验段进行，在实验段下部安装了专门为进行高速列车试验研制的带转盘的地板装置(见图1)，地板上表面距风洞下洞壁1.06 m，转盘中心距地板前缘7.84 m，距后缘8.26 m。地板前、后缘加工成流线型，以减少对气流的干扰；地板之间有倾斜的缝隙，以降低地板附面层的影响。在地板中间有一直径为7 m、可旋转360°的转盘，其他为固定部分，桥梁或路堤安装在转盘上。将实验段改造成实际空间为长×宽×高为 16.1 m×8 m×4.96 m、有效截面积为 39.2 m2的列车实验专用实验段。

本实验棚车以四节车编组形式进行，即：机车＋棚车＋棚车＋棚车。试验研究路堤和桥梁高度分别为5 m和15 m时车辆的气动力。

由于此次实验要求最大的侧滑角为 β=90°，故模型长度应小于实验段8 m的宽度，并且必须考虑风洞壁对模型的影响。据此，桥梁、路堤的模型长度取为7 m；而列车模型又需考虑桥梁、路堤对列车的影响，其最长不得超过5 m，从而模型缩尺比例定为1:15。在桥梁和路堤上还安装了路基、钢轨和枕木模型(见图2和图3)。经验算，阻塞系数均远小于5%，因此，模型缩尺比例采用1:15能在8 m×6 m风洞中较好地进行试验。

图1 风洞试验地板装置Fig.1 Floor equipment in wind tunnel

图2 在桥梁上棚车编组的风洞试验模型Fig.2 Box-car model on bridge in wind tunnel

图3 在路堤上棚车编组的风洞试验模型Fig.3 Box-car model on embankment in wind tunnel

1.2 风洞试验结果

在横风作用时，较大横向力和侧滚力矩可直接导致车辆的倾覆，升力的作用相当于减轻车辆的自身重力，使车辆抵抗倾覆的能力减弱，因此，研究了棚车的横向力系数、升力系数和侧滚力矩系数，其表达式为：

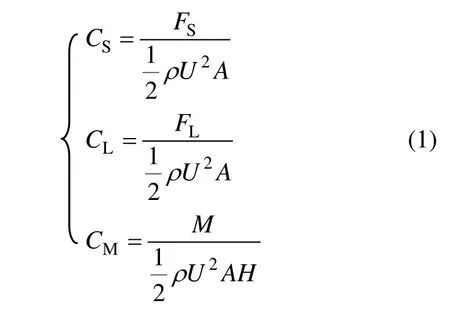
式中：CS为气动横向力系数；CL为气动升力系数；CM为倾覆力矩系数；FS为气动横向力系数；FL为气动横向力；M为倾覆力矩；ρ为空气密度，取20°时空气密度ρ=1.225 kg/m3；A为缩比模型棚车侧向投影面积，A=0.28 m2； H为参考高度，H=0.2 m； U为风速u和车速v的合成风速，，合成风速U分别为30，40，50和60 m/s；侧滑角β分别为0°，30°，45°，60°，75°和 90°。在变风速试验中，发现气动力系数不随风速的改变而改变，说明试验进入自模区。试验得到的气动力系数经过换算后得到实际棚车的气动力系数，如表1所示。

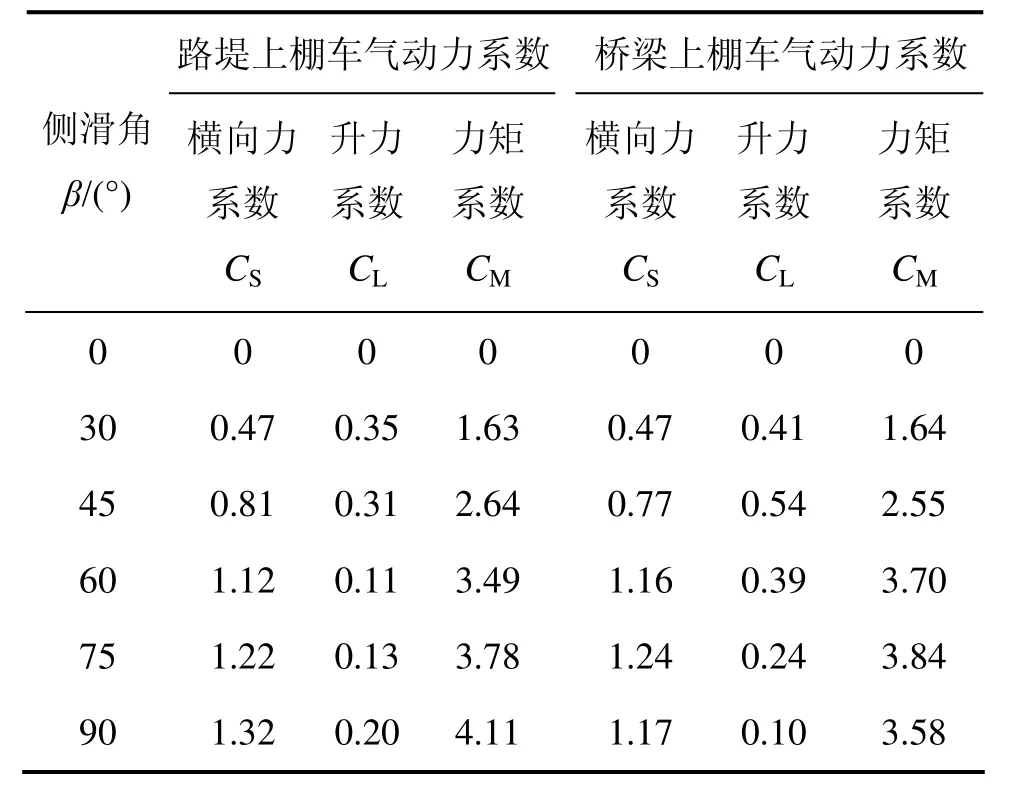
表1 测力试验得到的气动力系数Table 1 Aerodynamic coefficients gotten from force test

从表1可以看出：在路堤上时侧滚力矩系数CM、横向力系数CS、升力系数 CL均随着侧滑角的增大而增大；而在桥梁上时，当侧滑角为0°~75°时，气动力和力矩系数随着侧滑角的增大而增大，75°时到达最大，之后稍微降低。

2 车辆倾覆稳定性计算

2.1 车辆在轨道上的倾覆稳定性计算

车辆在运行过程中，主要受到气动横向力、气动升力、离心力、轮轨作用力、车体横向振动惯性力和重力的作用。其中，气动横向力和气动升力是由车辆迎风面和背风面等车体表面的分布压力和黏性力经积分合成得到。车辆受力图如图4所示。

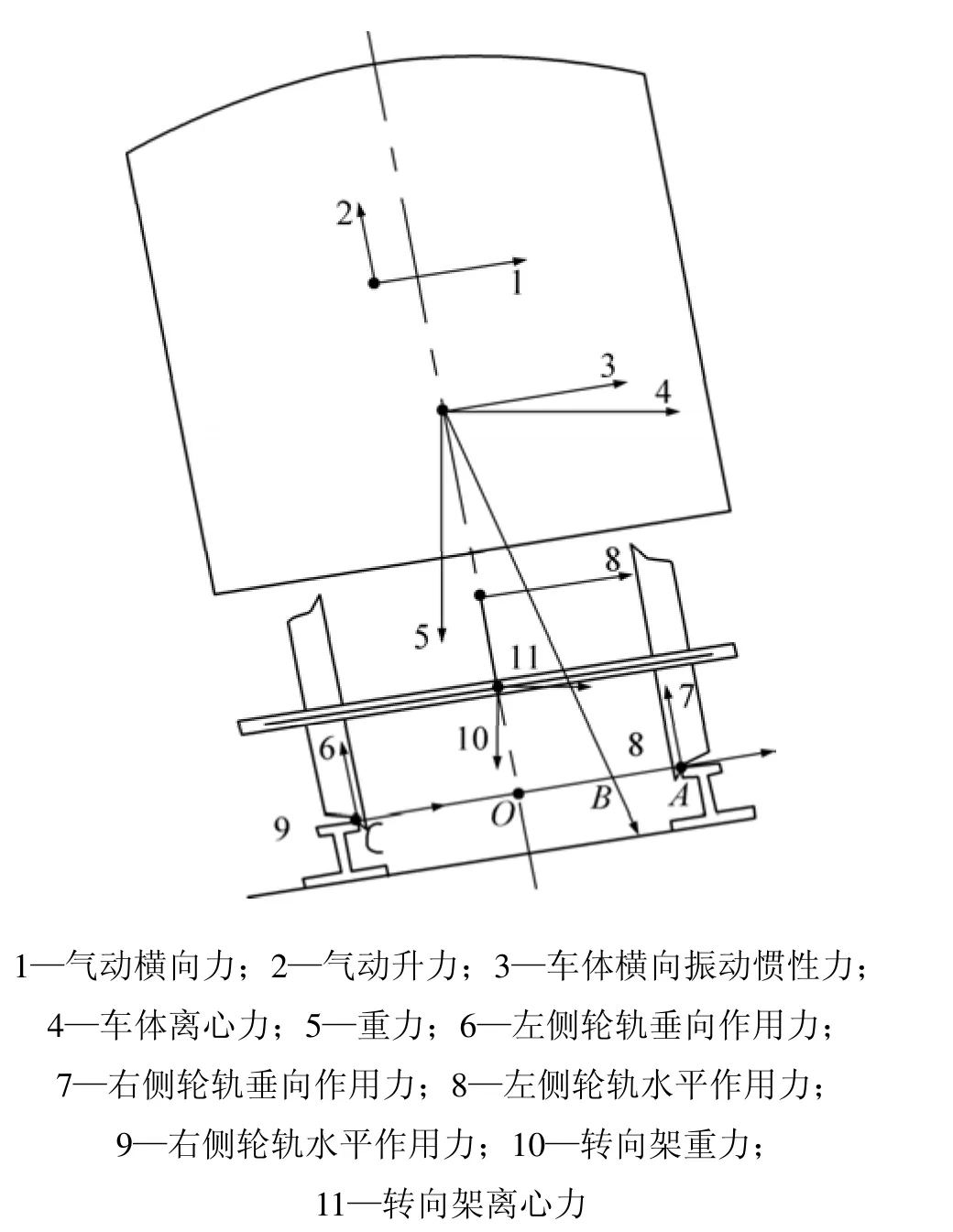
图4 车辆受力图Fig.4 Diagram of train force

在强风作用下，若所有合力的作用点通过B点，对B点取矩，则：

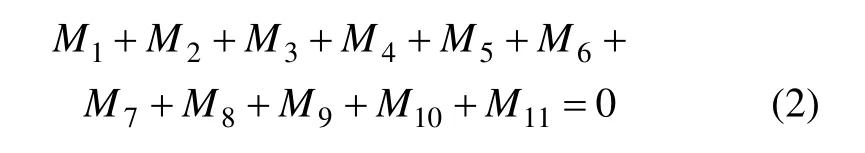
式中：M1为气动横向力 FS产生的力矩,FS=0.5ρ(u2+v2)SCS；ρ为空气密度，取海拔4 km时空气密度ρ=0.776 kg/m3，u为横风风速，v为车速，S为侧墙面积；M2为气动升力 FL产生的力矩，FL=0.5ρ(u2+v2)SCL；M3为车体横向振动惯性力 Fy2引起的力矩，Fy2=mcα；mc为车体质量；α为车体横向振动加速度；M4为车体离心力 Fy3产生的力矩，Fy3=mcv2/R, R为曲线半径；M5为车体重力Fz2产生的力矩，Fz2=mcg，g为重力加速度；M6为左侧轮轨垂向作用力Fz3产生的力矩；M7为右侧轮轨垂向作用力Fz4产生的力矩；M8为左侧轮轨水平作用力Fy4产生的力矩；M9为右侧轮轨水平作用力 Fy5产生的力矩；M10为转向架重力Fz5产生的力矩，Fz5=mbg，mb为转向架质量；M11为转向架离心力Fy6产生的力矩Fy6=mbv2/R；车辆参数见文献[18]。

式(2)中，左、右侧轮轨水平作用力Fy4和Fy5的力臂为 0，则 M8=0、M9=0；同时，由车辆的倾覆系数D[18]的定义可知：M6+M7=0。将气动横向力FS和气动升力FL产生的力矩合并为M，则M=0.5ρ(u2+v2)SCMH，H为参考高度。则式(2)可以写成：

式(3)即为车辆向曲线外侧倾覆的力矩平衡方程式。式(3)中：G为接触斑间距的一半；y为车辆重心的横向偏移，y=y1+y2+y3，y1为外轨超高引起的重心偏移，y2为横向力Fy2和Fy3使车体左右侧轴箱弹簧增减载引起的车体偏移，y3为气动侧滚力矩M使车体左右侧轴箱弹簧增减载引起的车体偏移；h1为车体的重心高；h2为转向架的重心高。

式(3)中，若大风从曲线外侧吹向曲线内侧且车辆向内侧倾覆，则图4中B点位于O点左侧，同时，横向振动加速度指向曲线内侧，即D，v，CS，CL和CM取反号。则式(3)可以写成：

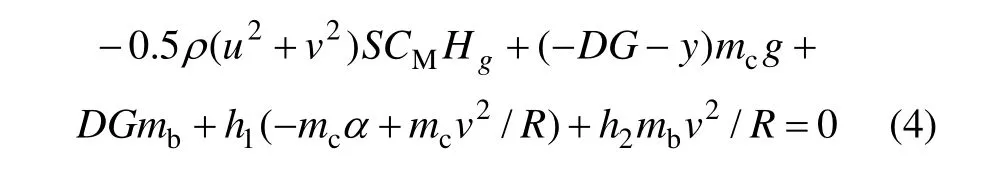
若车辆在直线上运行，则外轨超高引起的中心偏移y1=0，车体离心力Fy3=0，转向架离心力Fy6=0。

式(3)和式(4)中仅有车速v和风速u为未知量，求解式(3)和式(4)，得到车辆在转向架上倾覆时车辆运行速度和临界倾覆风速之间的关系，如图5所示。其中线路为曲线时，曲线半径R=600 m，外轨超高150 mm。

从图5可以看出：若车辆在曲线上运行，车辆在5 m高路堤和15 m高桥梁上的车速和风速关系曲线形状类似，车辆在路堤和桥梁上的临界倾覆风速分别为41.6和44.5 m/s；当车速为100 km/h时，其临界倾覆风速约为 35 m/s。若车辆在直线静止时，则其在路堤和桥梁上的临界倾覆风速分别为48.0和52.0 m/s；当车速为120 km/h时，在路堤或桥梁上棚车的临界倾覆风速接近38 m/s。同时从图5还可以看出：由于海拔较高时空气密度较小，在同样的气动力系数下车辆受到的气动力较小，因此，车辆的临界倾覆风速较高。

图5 车辆在轨道上倾覆时车速与临界风速之间的关系Fig.5 Relationship between train speed and critical wind speed of train overturning on track

2.2 车辆在转向架上的倾覆稳定性计算

车辆在转向架上的倾覆包括2种情况：当车辆的气动升力大于车辆的自重时，气动升力可以将车体向上吸起，可认为车辆发生倾覆；当车辆的气动升力小于车辆的自重时，车辆受到的力使车辆在转向架上倾覆。由于转向架和车体之间倾斜超出一定程度后一侧的旁承会接触，因此，以一侧的旁承为支点建立车辆的倾覆平衡方程式。参考式(3)，车辆在转向架上的倾覆的表达式可以表示为：

式(5)与式(3)的主要区别在于：式(5)中没有考虑转向架的影响。

式(5)中，若大风从曲线外侧吹向内侧且车辆在转向架上向内侧倾覆，则D，v，CS，CL和CM取反号，式(5)可以写成为：

若车辆在直线上运行，则外轨超高引起的中心偏移y1=0，车体离心力Fy3=0。

根据式(5)和式(6)可以得到车辆在转向架上倾覆时的车辆运行车速和临界风速之间的关系，如图6所示。

经验算，在每条曲线上，车辆受到的气动升力均小于车辆的重力，即车辆在转向架上倾覆之前不会被大风向上吸起。从图6可以看出：若车辆在曲线上静止时，车辆在路堤和桥梁上的临界倾覆风速分别为37.0和39.5 m/s；当车速为100 km/h时，临界倾覆风速接近30 m/s。若车辆在直线上静止时，其在路堤和桥梁上的临界倾覆风速分别为45.0和49.0 m/s，当车速为120 km/h时，在路堤或桥梁上棚车的临界倾覆风速接近33 m/s。从图5和图6可以看出：在车速相同时，车辆在转向架上更容易发生倾覆；因此，制订车辆限速标准时应当以车辆在转向架上的倾覆风速作为临界风速。

从图5和图6还可以看出：当车速v≤90 km/h时，风从曲线外侧吹向曲线内侧时的临界倾覆风速较风从曲线内侧吹向曲线外侧时的临界倾覆风速小，即车辆容易向曲线内侧倾覆。这主要是线路的外轨超高造成的。当风从曲线外侧吹向曲线内侧时，倾覆风速在车辆运行速度为60 km/h左右达到最小值。这主要是因为车辆在低速运行情况下，车辆的横向振动加速度随着速度的增加而增加，且占据主导地位，而当车速v＞60 km/h时，车辆在曲线上的离心力随着速度的平方的增加而增加，离心力抵抗车辆向内侧倾覆的能力增强，倾覆风速随着车速的增加而增加。

图6 车辆在转向架上倾覆时车速与临界风速之间的关系Fig.6 Relationship between train speed and critical wind speed of car-body overturning on bogie

3 结论

(1) 在路堤上当气动力系数和气动力矩系数在侧滑角β为0°~90°之间时，随着侧滑角的增大而增大；而在桥梁上时，侧滚角β在0°~75°时气动力系数和气动力矩系数随着侧滑角的增大而增大，之后稍微降低。

(2) 车体在转向架上倾覆的临界风速小于车辆整车在轨道上倾覆的临界风速，车辆的安全速度限值应当以车体在转向架上倾覆为前提。当车辆在曲线上静止时，车辆在路堤和桥梁上的临界倾覆风速分别为37.0和39.5 m/s；当车速为100 km/h时，其临界倾覆风速为30 m/s。当车辆在直线上静止时，其在路堤和桥梁上的临界倾覆风速分别为45.0和49.0 m/s；当车速为120 km/h时；在路堤或桥梁上棚车的临界倾覆风速接近33 m/s。

(3) 车辆在路堤上运行或在桥梁上运行时，车辆的车速和风速关系曲线趋势相同。当车速v≤90 km/h时，风从曲线外侧吹向曲线内侧时的临界倾覆风速较风从曲线内侧吹向曲线外侧时的临界倾覆风速小；当车速v＞90 km/h时，情况正好相反。

(4) 由于高原空气密度较低，在气动力系数相同时，若车辆受到的气动力较小，则车辆相对不容易发生倾覆。

[1] 任建. 青藏铁路客车的几点思考[J]. 铁道车辆, 2003, 41(10):