基于多采样率定时比较技术的并联有源滤波器

侯 睿 郭伟峰 武 健 徐殿国

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

1 引言

有源电力滤波器能够治理电网中的谐波污染，同时能对系统进行快速无功补偿，改善电能质量，从而受到了越来越广泛的研究和关注。并联有源电力滤波器的基本原理[1-2]是检测电网中的无功和谐波电流，同时向节点注入幅值相等、相位相反的电流，从接入点向后看，系统中只剩下基波有功电流。

无功和谐波的检测通常使用赤木泰文提出的瞬时无功功率理论[3]，而控制方法上主要有两类[4-6]：一类是滞环比较控制，即电流直接跟踪PWM控制，定时比较控制是其应用于数字控制系统中的特例；另一类控制方法是三角波调制 PWM技术。前者的优点是响应速度快，系统鲁棒性好，控制简单实用，从而在工程上取得了广泛的应用；不足之处在于开关频率不固定，与环宽或者定时周期有关。后者开关频率固定，然而响应较慢，调节精度较低。近年来，数字信号处理技术取得了飞速的发展，定时比较法本身具有实现简单，节省硬件资源的优点。然而，传统的单采样速率定时比较法控制效果受参考值计算速度的制约，难以取得令人满意的结果。

多速率采样技术是数字控制系统研究的新热点之一，它可以实现单采样率系统所不能实现的许多功能，诸如同时稳定、强镇定、分散控制，还能改善系统的裕度增益[7-10]。文献[8]全面总结了多采样系统的分类和特点，给出了设计多采样系统的准则。文献[10]将其应用于直接转矩控制系统中，取得了令人满意的控制效果。目前来看，关于多采样技术在有源滤波器中应用的文献十分少见。

本文试图将数字控制系统中的多速采样技术应用于有源滤波器的控制当中，通过对制约传统单采样率定时比较技术的因素进行分析，设计出利用多采样率技术改善系统性能的方案，并通过仿真和实验加以验证。

2 系统的基本原理

有源滤波器（APF）的结构简图如图 1所示。电压型逆变器通过电抗器L接入电网，L起着抑制高频电流的作用。此处也可用LCR或LCL滤波器代替单电感滤波，好处是降低了所需的电感值，节省空间和成本。然而本文所研究的定时比较控制方法开关频率是不固定的，设计开关噪声滤波器的参数难度较大，所以仍然采用单电感滤波。

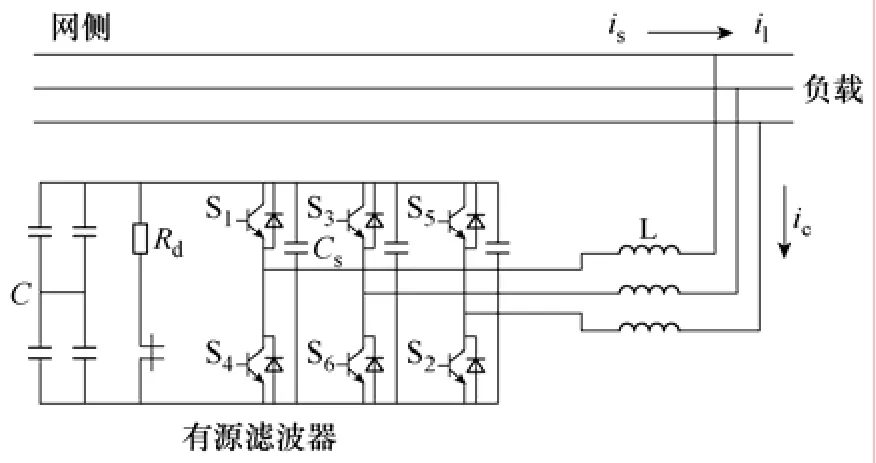
图1 有源滤波器结构Fig.1 Structure of active filter

设逆变器直流母线电压为 Udc，电网相电压有效值为 Us，考虑到 SPWM 方法的直流电压利用率为 0.707，将逆变器输出的交流相电压折算成有效值，则APF发出的最大电流有效值Icmax可以近似地由下式计算：

滤波电感越小，系统的容量可以做得越大，同时可以提升电流的跟踪速度。然而，电感过小将导致输出电流中的高次谐波不能被有效抑制，波形质量变差。设计时电感的取值应综合考虑以上因素。如果检测网侧电流，提取其中无功和谐波乘以增益K作为给定，属于闭环控制，K取得过大系统将不稳定，反之精度则无法保证。采用检测负载电流的方法鲁棒性要远好于检测网侧电流方式。选用瞬时无功功率理论中的ip−iq法，负载电流减去基波有功电流反变换的各相分量作为每相的给定。

低通滤波器（LPF）的设计极大地影响有源滤波器的性能。一方面，LPF的截止频率应该足够低，保证提取出的基波有功电流平滑，才能使计算出的谐波给定准确。由于电力系统中常见的5、7次谐波在ip−iq法中以6次谐波形式叠加在ip通道上，所以要保证滤波器对6次谐波的抑制比足够大。另一方面，如果滤波器的阶跃响应过慢，有源滤波器的快速性将受到较大影响。同时，直流母线的电压更易受负载的变化而波动。可选用二阶巴特沃兹滤波器。

3 单采样率定时比较技术分析

定时比较技术每隔一个定时周期比较参考值与反馈值的大小，同时进行相应的调节。与硬件滞环控制相比，只需一个数字信号处理器（DSP）就可以实现，同时限制了逆变器开关频率的大小，即开关频率最大不会超过定时频率的一半。但是它的主要问题是逆变器输出电流的误差是不定的，对于有源滤波器来说，这会直接影响滤波效果。

由于APF交流输出为双极性的PWM波形，对于每一相来说，APF交流电感两端的电压

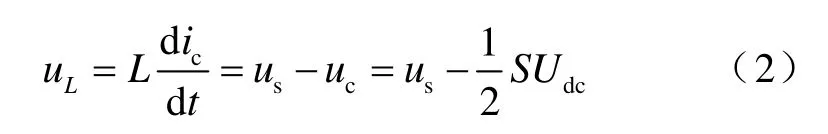
式中，us和uc分别为电网和逆变器输出瞬时电压，S为该相的开关函数，定义S为

设 T为系统的采样周期，于是得到在 kT时刻APF电流变化的斜率

从式（4）中可以看出，APF电流的变化率与直流母线电压大小和交流电抗有关。通常选取合适的交流电抗和直流母线电压值，保证APF电流具有足够陡峭的斜率，从而提高APF电流的跟踪能力。此外，从式中还可以看出，电流上升和下降的斜率是不等的。当电网电压为正极值时，电流上升斜率与下降斜率绝对值之比最大，反之则反是。

图2为有源滤波器定时比较控制的示意图。实际上，为了分析简便，假定给定值在较短的时间内保持不变。当时间间隔足够短时，可以认为APF电流是线性变化的。以 APF某电流极小时刻为零时刻，以给定值为横轴，则电流从(0,icmin)经过m个控制周期T达到极大值(m T,icmax)。令电流上升的斜率为p，下降的斜率为h。定义高斯向上取整函数Ceil(x)==F +1，当 F＜x≤F+ 1，F∈N时。设Tc为APF开关周期，利用解析几何的方法易求得

图2 定时比较原理Fig.2 Principle of timer comparison

Tc作为T的函数来讲，取整函数存在许多畸点，在这些点上Tc不可导。Tc对T不具有一致的单调性。然而，在绝大部分点的邻域内，Tc对T是增函数。从期望的角度来看，减小控制周期T，就会减小开关周期Tc。实际上，在其他条件（电抗值、压差值）一定时，减小T，很大可能会降低APF电流超出给定值的超调量，从而尽快地回调至给定，完成一次开关周期。

数字控制系统中，采样频率要按照香农定理选择，即采样频率应至少为信号频谱中最高有效频率的两倍。实际应用时，为了取得良好的效果，一般至少应为5～10倍。假设APF要补偿20次以内的谐波，则采样频率至少应为5kHz。

所谓单采样率系统，即所有数字量的采样和保持均以相同的频率进行。通常的流程为DSP在定时或捕获中断开始时同步采样各路信号，包括A相电压uA，负载电流il，APF电流ic，直流母线电压Udc等，再利用数学方法计算出各相的无功和谐波给定，之后比较输出，即APF控制周期和采样周期相等。然而，不管用什么数学方法，计算给定都需要多步浮点数乘除法运算，需要占用大量的时间。设计算给定的时间为T0，则系统的最高控制频率只能做到1/T0，且DSP通常还有许多其他任务，比如和人机交互单元的通信，软件压力较大，在这种策略下想获得很高的控制频率是很困难的。此外，由于比较的是T0之前的ic值和给定，会使系统产生额外的延迟，加上数字控制系统本身固有的迟滞，整个系统的延迟时间在一拍以上。这将使APF系统的控制能力较低，如前面所分析的一样，电流的过调将增大，开关频率不高。

4 多采样率定时比较技术分析

多采样率系统是指对被控对象的输入和输出各量按照不同的速率采样的数字控制系统。在一定范围内提高采样速率可以增强对被控对象的控制能力，然而各物理量的变化速率不同，如果不分别对待，势必会使某些量处于“欠控”态，而某些量处于“过控”态，从而影响整个系统的性能。设系统采用的都是零阶保持器，被控对象的输入u按照采样周期Tu保持，输出y按照采样周期Ty采样。如果Tu＞Ty，则称系统为输出多采样系统，否则称为输入多采样系统。实际系统输入输出量有很多，若输入或输出的各分量采样速率不同，则称为广义多采样控制系统。实际应用时，常令Tu和Ty成整数倍关系，称两者中较大值为系统的框架周期，记为Tm。

下面以APF实际系统为例，设计一套便捷有效的多采样率控制方法。

首先，以数字信号处理器（DSP）为控制器，以APF和电网为被控对象，以控制系统的无功和谐波为目标，以0为给定。那么整个控制系统的输入输出量采样关系如图3所示。

图3 多采样系统Fig.3 Multirate sampled system

计算无功和谐波的给定需要采集负载电流il和电网A相电压uA，由于这是系统中最耗时的环节，取它们的采样周期为框架周期Tm。直流母线电压调节是叠加在ip通道上的，而且电压的控制并不需要十分高的速度，取 T4=Tm即可。根据前面的分析，提高APF的控制频率可以提高逆变器的开关频率，相当于提高了 APF的带宽。因此期望 DSP的开关输出S的周期尽量短，可以取Tu=N Tm。其中N成为多采样重数。同时根据系统的原理可知，在一个框架周期内，必须要采集N次 APF电流 ic，于是取T3=N Tm。这个系统是一个周期时变的广义多采样系统，它在一个框架周期内只计算一次给定值，却完成了N次对被控对象的控制，从而较单采样系统有更强的控制力。同时，较整体提高采样频率而言，在一个框架周期内会节省出更多的时间让DSP完成其他的重要工作，软件压力较小。

这种控制是否合理呢？答案是肯定的。首先，设计 APF电抗时，要使 APF电流的平均变化率远大于电网中电流变化率。所以对APF输出电流采用更高的采样频率是合理的。其次，当Tm满足香农采样定理设计要求时，它已经能完全复现系统中的无功和谐波信息，且当Tm足够小时，可以认为在很短的时间内给定相对于ic是不变的，此时仅根据ic的采样对APF的控制是有效的。最后，APF注入电网中的电流不会影响 il即自身给定，所以这属于开环控制，没有稳定性的问题。当然，N不宜取得过大，过高的比较速率会放大系统的噪声，提高系统的开销。实际应用时，N取2较好。

多采样系统在DSP软件中很容易实现，可在每个框架周期内实现两次定时Tm/2的中断，每次只需要采集两相APF电流，完成一次比较即可，软件开销很小。而且利用即时的APF电流比较，可以减小传统同步单采样系统的延时。该法相当于用最小的开销提高了系统的有效控制频率。图4为双采样技术和单采样技术的比较示意图。可以看出，采用了双采样技术之后，系统的开关频率提高，APF输出的电流波形质量会更好。

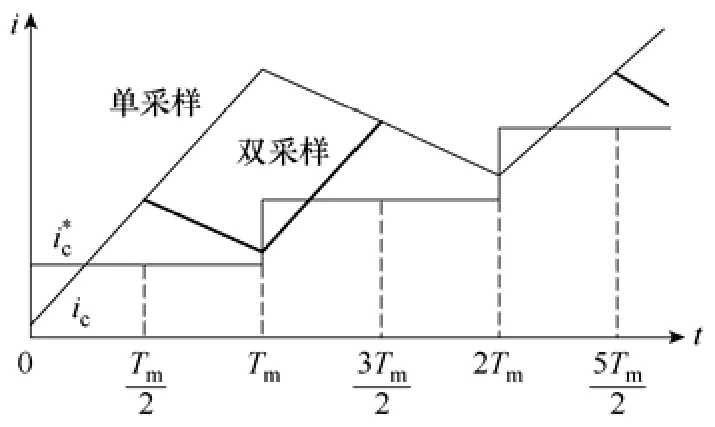
图4 双采样系统Fig.4 Double sampled system

5 仿真与实验分析

为了验证多采样方法对APF输出电流的影响，在Matlab的Simulink仿真环境下搭建了系统的仿真模型。设负载侧电阻为10Ω，负载电抗器为100mH、50mH、25mH三组，可以在任意时刻分组投入模拟系统的无功变化。设定系统的框架周期Tm=1/(12.8kHz)。对于基频来看，一个周期采样256个点，根据香农采样定理，至多可以重现频率为6.4kHz以下的信号，显然框架周期的设计是合理的。

分别利用框架频率12.8kHz实现的单采样和双采样实现APF，投入了100mH和50mH两组电抗，图5对比了补偿后网侧电流的波形和频谱。

图5a为单采样时网侧电流的波形。可以明显看出电流的纹波较大，开关频率较低。由频谱分析来看，开关频率集中在1～3kHz之间。图5b为双采样时的电流波形。从图中可以看出电流的纹波明显减小，开关频率在3kHz以上的成分仍然有许多，带宽较单采样时有较大提高。从电流THD来看，单采样电流THD为14.83%，双采样的THD降为6.70%，波形质量更好。

为了实际验证双采样算法的效果，编制了DSP程序，利用实验室的并联APF样机做了相关实验。相关参数如下：APF交流输入 380V，直流母线720V，APF连接电抗4mH。无功源电抗器参数与仿真中的一致，用整流桥带电阻负载充当谐波源。

利用3196测试仪分析APF补偿无功后网侧C相电流的频谱，3196最大可以分析到 2.5kHz。图6a为12.8kHz单采样时的波形，从频谱看出，2.5kHz以内的开关纹波成分很大，波形质量不高。图 6b为12.8kHz框架频率下双采样时的波形，从频谱看出，2.5kHz以内开关纹波极小，开关纹波应该分布在更高的频域内，波形的质量也较为理想。

图5 仿真波形Fig.5 Simulation waveforms

图6 实验波形Fig.6 Experimental waveforms

图7为APF利用双采样算法补偿整流桥谐波源的波形。il为负载侧A相电流，ic为APF输出B相电流，is为网侧C相电流。

图7 补偿谐波波形Fig.7 Waveforms of harmonic compensation

从上图中可以看出，经过有源滤波器的作用，网侧电流波形明显改善。3196电能质量分析仪记录显示系统的主要谐波，即6k±1次电流的幅值在补偿后都大幅下降，电流THD也由29.57%降为7.67%。当然，如果适当将系统框架频率12.8kHz提高的话，根据采样理论，系统有效控制频率也将随之提高，同时量化误差对系统的影响将更小，补偿效果将会更好。

6 结论

通过分析发现，传统单采样率APF的开关频率在很大程度上与系统的采样周期有关。提高采样频率可以提升APF的性能，然而实际系统中计算给定参考值占据了控制周期的大部分时间，利用传统的单采样率技术难以实现期望的指标。本文提出了将数字控制系统中的多采样技术应用至 APF控制系统中的控制方法，在一个框架周期内计算一次给定值，完成多次定时比较，从而提高了系统控制频率。分析了它的合理性，并利用仿真和实验验证了双采样算法较单采样算法的优越性。仿真和实验表明双采样率APF具有更高的频带和更小的电流纹波。

[1]王兆安,杨君,刘进军.谐波抑制和无功功率补偿[M].北京: 机械工业出版社,1998.

[2]Singh B,Saha R,Chandra A,et al.Static synchronous compensators (STATCOM): a review[J].IET Power Electronics,2009,2(4): 297-324.

[3]Akagi H,Watanabe E H,Aredes M.Instantaneous power theory and applications to power conditioning[M].New York: John Wisley and Sons Inc.,2007.

[4]杨秋霞,梁维国,郭小强,等.准谐振控制器在有源电力滤波器中的应用[J].电工技术学报,2009,24(7): 171-176.Yang Qiuxia,Liang Weiguo,Guo Xiaoqiang,et al.Application of quasi resonant controller for active power filter[J].Transactions of China Electrotechnical Society,2009,24(7): 171-176.

[5]张宪平,林资旭,李亚西,等.LCL滤波的PWM整流器新型控制策略[J].电工技术学报,2007,22(2):74-77.Zhang Xianping,Lin Zixu,Li Yaxi,et al.A novel control strategy for PWM rectifier with LCL filter[J].Transactions of China Electrotechnical Society,2007,22(2): 74-77.

[6]张加胜,李浩光.基于滞环控制的电压型变流器开关频率分析[J].电力系统及其自动化学报,2008,20(2): 57-59.Zhang Jiasheng,Li Haoguang.Switching frequency analysis of voltage source converter based on hysteresis current control[J].Proceedings of the CSU-EPSA,2008,20(2): 57-59.

[7]肖建.多采样率数字控制系统[M].北京: 科学出版社,2003.

[8]Seung Hi Lee.Multirate digital control system design and its applications to computer disk drives[J].IEEE Transactions on Control System Technology,2006,14(1): 124-133.

[9]肖建,徐志根.多采样数字控制系统综述[J].信息与控制,2003,32(5): 436-441.Xiao Jian,Xu Zhigen.Survey on the research of multirate digital control systems[J].Information and Control,2003,32(5): 436-441.

[10]蔡华斌,肖建,严殊.基于 DSP的多采样率直接转矩控制系统研究[J].中国电机工程学报,2008,28(27): 114-119.Cai Huabin,Xiao Jian,Yan Shu.Multirate direct torque control based on DSP[J].Proceedings of the CSEE,2008,28(27): 114-119.