改进加窗频谱峰值拟合算法及谐波分析应用

温 和 滕召胜 黎福海 王 永 胡晓光

（1.湖南大学电气与信息工程学院 长沙 4100822.北京航天航空大学自动化工程学院 北京 100191）

1 引言

电力系统中，谐波的准确检测能够为谐波源定位、谐波治理、电能质量管理等提供科学依据，对电力系统的安全与稳定运行具有重要的意义[1-3]。快速傅里叶变换（FFT）因其易于实现，是目前最主要的电力谐波分析方法，但非同步采样时，FFT固有的频谱泄漏和栅栏效应影响了谐波参数（幅值、相位、频率）估计的准确性[4-6]。

国内外学者研究并提出了基于Hanning窗[7-8]、Bl ackman-Harris窗[9]、 Rife-Vincent窗[10]、 Nutt all窗[11-12]、矩形卷积窗[13-14]、三角自卷积窗[15-16]（Triangular Self-Convolution Windows，TSCW）等的加权电力谐波分析方法，在一定程度上提高了谐波检测的准确度[17-18]。但是采用上述窗函数进行谐波参数分析时，仍存在离散频谱辨识困难、修正公式求解复杂、计算准确度低等问题[19-20]，特别是对弱信号提取或对复杂信号进行分析时仍存在较大误差。

在对非同步采样和非整周期截断时的信号频谱进行分析的基础上，本文结合三角自卷积窗的频谱特性，采用最小二乘法（Least Square Method，LSM）逼近谐波参数分析的多项式，建立简便、易行且可根据计算精度要求进行调节的谐波幅值、频率、初相角参数计算式，该方法具有计算量小、实时性高、易于嵌入式系统实现的优点，较好地解决了非同步采样时离散频谱校正中存在的计算准确度与实时性的矛盾。仿真结果表明：在非同步采样和非整周期截断的条件下，本文算法能有效消除各次谐波相互干扰、抑制白噪声和基波频率波动对谐波参数分析的影响，提高谐波参数分析准确度。

2 频谱泄漏与三角自卷积窗函数

2.1 非同步采样时的频谱泄漏和栅栏效应

考虑一个周期为T、包含H次谐波的离散信号

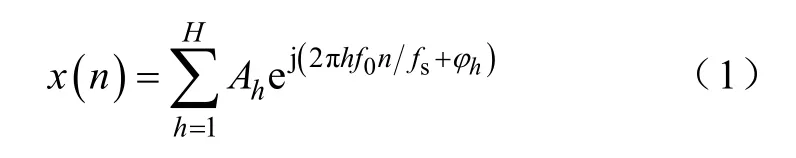
式中，h为谐波次数；f0=1 T代表基波频率；Ah、ϕh分别代表第h次谐波的幅值和初相角；为采样频率； n =0,1,…, N−1。

信号在观测周期Tw转换为 N点离散序列相当于被矩形窗wR(n)截断，其离散傅里叶变换为

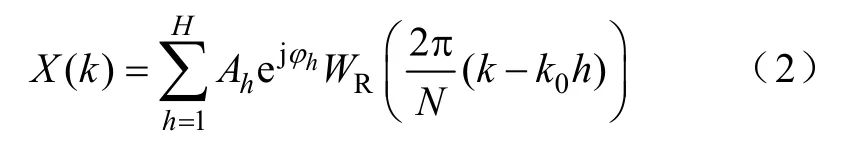
同步采样时，观测周期Tw为信号周期T的整数倍。而非同步采样时，离散频谱中信号各次谐波频率与频率分辨率之间不再为对应的整数倍关系，即出现所谓的栅栏效应。信号各次频率分量不再是单一谱线，而是分布于整个频率轴，即能量不再集中，并向临近谱线泄漏，即所谓的频谱泄漏现象。

非同步采样情况下直接采用FFT进行谐波参数分析，即直接利用频谱峰值计算谐波参数时，频谱泄漏和栅栏效应引起的误差较大。此外，非同步采样时，若信号包含有多个频率分量，则其各频率分量会产生泄漏叠加干扰（矢量之和），影响谐波参数检测的准确度。

2.2 三角自卷积窗与频谱泄漏抑制

由式（2）可知，频率 f0处的频谱形状等于信号截断时所加窗函数的窗谱形状。因此，通过选择窗函数减少频谱泄漏，降低谐波分量之间的相互干扰。三角自卷积窗wT(n) 具有优良旁瓣性能，可由若干个三角窗wg(m) 进行自卷积运算获得[23]，即

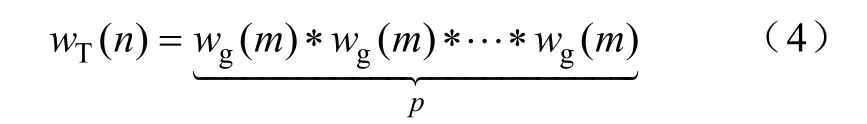
式中，n∈[0,N−1]；m∈[0,M−1]；p为参与卷积的三角窗的个数，称为窗的阶数。为便于计算，卷积运算后可对序列进行补零，将p阶三角自卷积窗的长度调整为N=pM。

根据卷积定理，函数在时域进行卷积等效于频域相乘，因此p阶三角自卷积窗的频率响应为

图1给出了三角窗（M=128）进行1～4阶自卷积得到1～4阶三角自卷积窗的幅频响应曲线。图1中标注了各阶三角自卷积窗的旁瓣峰值电平和旁瓣衰减速率。

图1 p阶三角自卷积窗幅频响应Fig.1 Frequency responses of the p-order TSCW

表1为4阶和8阶三角自卷积窗与常用窗函数在主瓣宽度、旁瓣峰值电平和旁瓣衰减速率等方面的比较。由图1和表1可见，三角自卷积窗的旁瓣电平与衰减速率随卷积阶数的升高而加强；与现有经典窗函数相比，三角自卷积窗具有较好的旁瓣峰值电平和旁瓣衰减速率，能有效减少频谱泄漏引入的误差。

表1 窗函数性能比较Tab.1 Comparison of window characteristics

3 基于LSM的离散频谱峰值拟合算法

3.1 基于TSCW的离散频谱峰值校正原理

对式（1）所示信号 x(n) 加三角自卷积窗后，其加窗离散傅里叶变换为

式中，k =0,1,L,N−1；WT(*)是三角自卷积窗的离散频谱函数。

不失一般性，设当前测量的为第h项谐波（h≤H），为简单起见，忽略其余各次谐波对第h项谐波的泄漏影响，此时，式（6）变为

设第h项谐波的频率hf0在离散频谱中对应的位置为hk0处，即 hf0=hk0Δf。参见图2，非同步采样时，hk0为非整数，即第h项谐波频率hf0与离散谱线不重合，且位于离散频谱幅值最大谱线k1和次大谱线k2之间（k1≤hk0≤k2=k1+1）。

参见图 2，令这两条峰值谱线的幅值分别为y1和y2，即

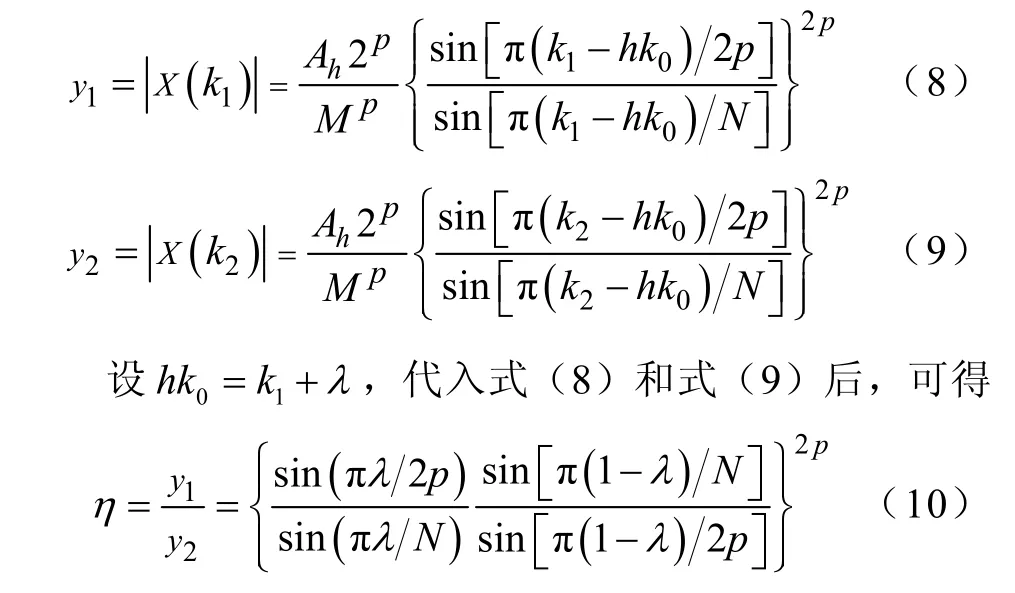
式（10）即为第h项谐波离散频谱的峰值谱线（第k1与k2根谱线）与真实频率谱线（第hk0根）的相对位置参数λ的约束条件。因此，理论上，可通过对离散频谱峰值进行校正，得到参数λ，从而实现谐波参数求解。

图2 非同步采样时离散频谱的栅栏效应Fig.2 Picket fence effect of the spectral with non-synchronized sampling

3.2 基于LSM的离散频谱峰值拟合算法

式（10）为复杂的有理式，若直接求其反函数，计算量较大。此外，式（10）建立的基础是忽略谐波间的相互泄漏影响，仅考虑非同步采样引起的频谱泄漏，即所描述的频谱峰值与相对位置参数λ之间的关系为一种近似关系。因此，本文考虑采用基于LSM的多项式拟合方法获得求解λ的计算式。

根据式（10），取L组待拟合试验数据(ηi, λi)（i=0,1,L,L−1），由于待拟合试验数据本身存在偏差，因此不要求拟合多项式λ=S(η)经过所有已知待拟合数据点(ηi,λi)，而仅要求在给定点ηi上的误差γi=S(ηi)−λi按误差平方和最小，即

显然，式（12）为 a0,a1,…,aK的多元函数，因此多项式拟合过程即为求式（12）极值的过程。由多元函数求极值的必要条件可得

式中，j =0,1,…,K−1。

由式（13）建立了关于a0,a1,L,aK的线性方程组，解出系数ak，从而可得基于 LSM的频谱峰值拟合多项式 SK(η)。

3.3 精度可控的多项式拟合与谐波参数求解算法

由于 hk0=k1+λ，可知λ取值范围为[0，1]，在该范围内取一组λ 值，可由式（10）得到对应的一组η值，即建立待拟合试验数据(ηi, λi)。根据式（13），可求解拟合多项式系数 a0,a1,…,aK。

工程实践中，可以根据测量精度的要求确定基于LSM的拟合多项式的次数。为确保谐波参数计算实时性，拟合多项式一般不超过7次。根据式（13），得到的基于4阶三角自卷积窗的频谱峰值最小二乘拟合5次多项式为

式中，参数 λ的拟合误差为 9.1587×10−5。

基于4阶三角自卷积窗的频谱峰值最小二乘拟合6次多项式为

式中，参数λ的拟合误差为 1.7016×10−5。

基于4阶三角自卷积窗的频谱峰值最小二乘拟合7次多项式为

式中，参数λ的拟合误差为3.3323×10−6。

由于第h项谐波对应的真实频率谱线位置应为第h k0根，因此第h项谐波的频率为

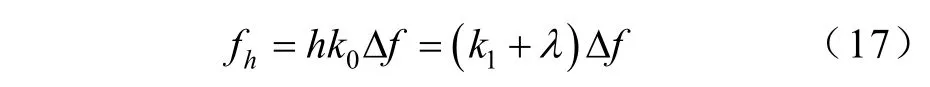
由式（10）可得，第h项谐波的幅值计算式为

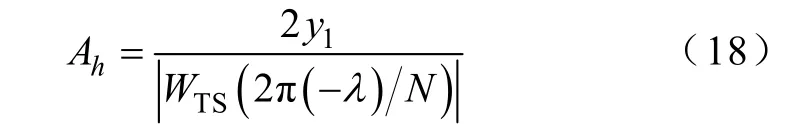
同理，可得第h项谐波的初相角为

信号中基波和各次谐波分量参数的计算可按上述过程逐次计算。

4 仿真与分析

4.1 复杂信号的谐波分析

采用文献[12]给出的含 2～21次谐波的信号进行分析

式中，基波频率f1=50.5Hz；采样频率fs=2500Hz；基波和各次谐波的幅值Ah和初相位hϕ在表2中给出。仿真实验结果由表3和表4给出，其中a E-b代表a×10−b。其中 Blackman、Blackman-Harris、Nuttall窗采用的数据长度为N=512；4阶三角自卷积窗分别长度为N=512和N=1024（最小二乘多项式拟合次数均为7次）。

表2 复杂信号的基波及谐波参数Tab.2 Parameters of the simulated harmonic signal

表3 幅值与频率相对百分比误差Tab.3 Percentage relative errors in calculating amplitude and frequency（%）

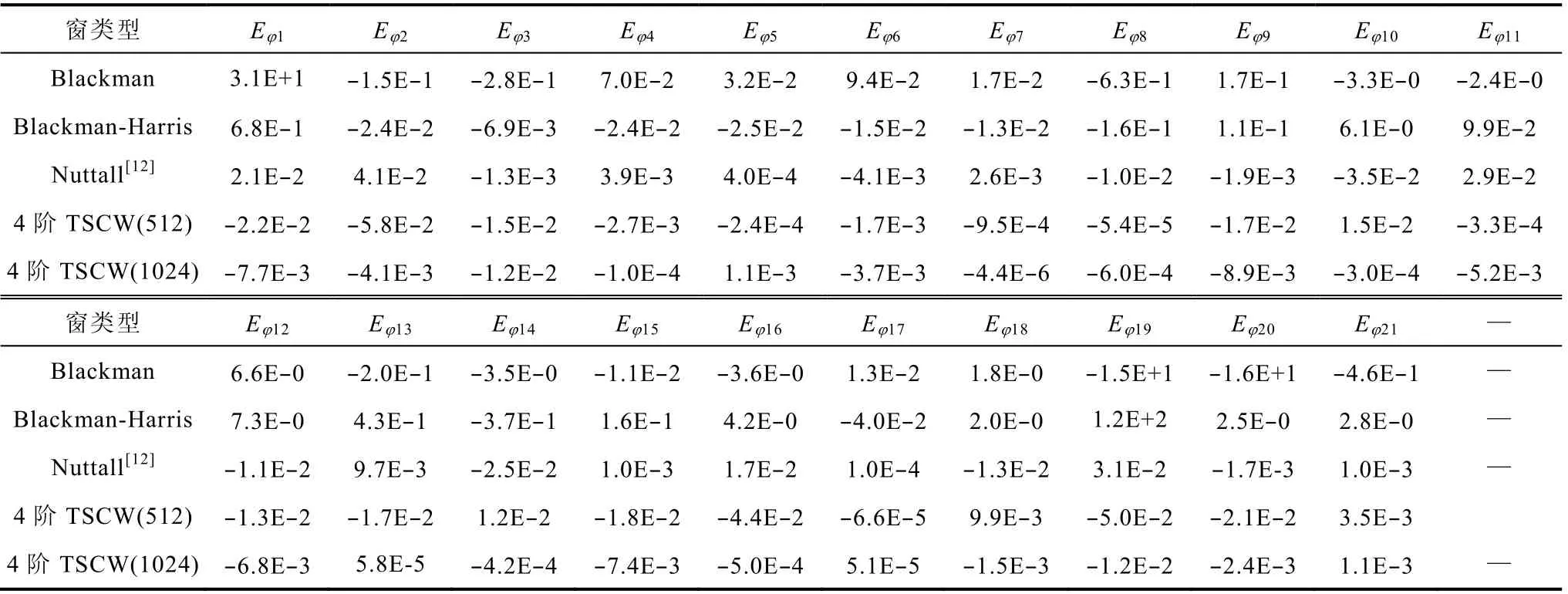
表4 初相位测量相对百分比误差Tab.4 Percentage relative errors in calculating phase（%）

表3中，Ef1表示基波频率的测量值相对于真值的误差。由表3和表4可见，采用4阶三角自卷积窗进行加权，利用本文提出的多项式拟合算法进行离散频谱校正后，N=512时频率计算的相对百分比误差为2.9×10−7%，N=1024时频率计算的相对百分比误差为-6.4×10−9%。当 N=1024时，幅值相对误差EAh≤0.00094%，相位相对误差Eφh＜0.012%，可实现复杂谐波信号参数的高准确度分析。与Blackman窗、Blackman-Harris窗和 Nuttall窗相比，基于 4阶三角自卷积窗的最小二乘多项式拟合频谱校正算法具有更高的谐波分析准确度，且计算简单，易于实现。

4.2 白噪声影响下的谐波分析

在白噪声存在的情况下，对式（20）所示的信号添加白噪声，信噪比（SNR）的范围为[10dB，100dB]，变化步长为10dB。分别采用Blackman窗、Blackman-Harris窗、Nuttall窗和本文算法（4阶三角自卷积窗N=512和N=1024）进行谐波参数估计。以幅值微弱的第21次谐波分析为例，图3～图5分别给出了白噪声存在情况下幅值、初相角、频率的绝对误差曲线。

参见图3～图5，白噪声对相角估计准确度存在一定的影响。当信噪比＜50dB时，采用 Blackman窗、Blackman-Harris窗和四项三阶Nuttall窗均存在较大误差；当信噪比＞50dB时，采用Blackman窗、Rife-Vincent（I）窗和 Nuttall窗获得的幅值、初相角、频率分析准确度有所提高，采用本文算法的准确度最高。由仿真结果可见，采用本文算法可以有效减少白噪声对谐波分析准确度的影响，如在信噪比水平为[50dB，100dB]范围时，采用本文算法可实现谐波参数的准确分析。

图3 白噪声情况下第21次谐波幅值分析绝对误差Fig.3 Absolute errors of amplitude with white noise of the 21st harmonic

图4 白噪声情况下第21次谐波初相角分析绝对误差Fig.4 Absolute errors of phase with white noise of the 21st harmonic

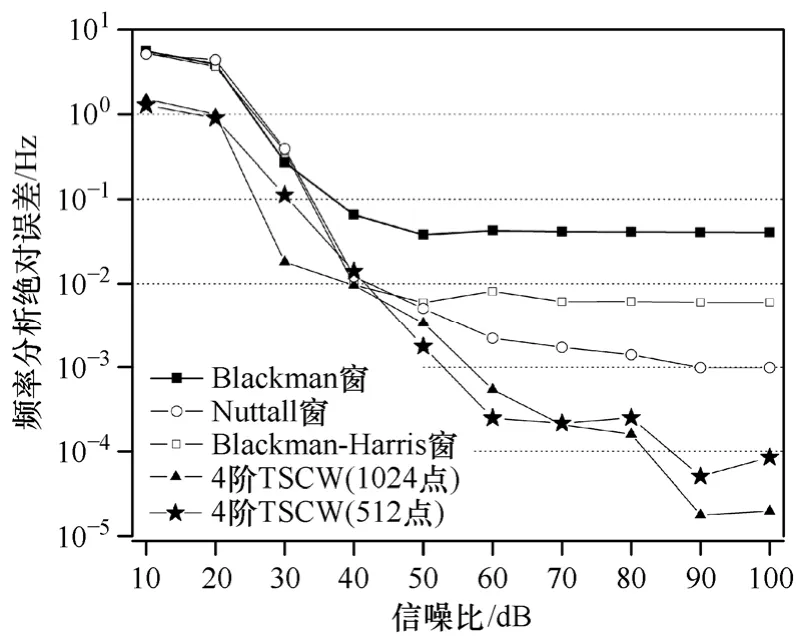
图5 白噪声情况下第21次谐波频率分析绝对误差Fig.5 Absolute errors of frequency with white noise of the 21st harmonic

4.3 基波频率变动下的谐波分析

实际应用中，电网基波频率并非恒定，往往存在小幅波动。设基波频率波动范围为[49.5Hz，50.5Hz]范围，步长为 0.1Hz，采用本文算法（4阶三角自卷积窗N=512）对式（20）所示的信号进行谐波参数分析。图6和图7分别给出了基波频率波动情况下基波和各次谐波幅值和初相角的绝对误差分布情况。

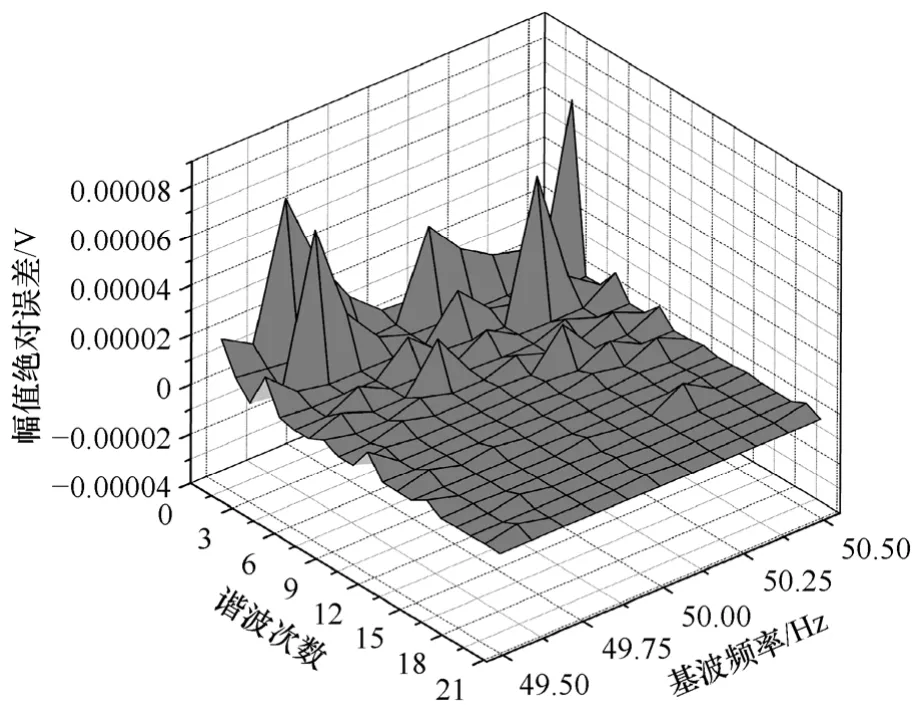
图6 基波频率波动时基波与谐波幅值分析绝对误差Fig.6 Absolute errors of amplitude with frequency changing of fundamental and harmonic components

图7 基波频率波动时基波与谐波初相角分析绝对误差Fig.7 Absolute errors of phase with frequency changing of fundamental and harmonic components

由图6和图7可知，当基波频率发生波动时，谐波参数分析的准确度受到一定程度的影响。图 6和图7中，第2次谐波参数分析的准确度受基波频率波动影响最大，主要原因是第2次谐波幅值较弱，且临近幅值最大的基波分量，受频谱泄漏和栅栏效应影响较大。仿真结果表明，在基波频率波动情况下，采用本文算法实现较为准确的谐波参数分析，基波和各次谐波幅值分析绝对误差＜0.00005V，初相角分析绝对误差＜0.075°，可满足实际测量要求。

5 结论

针对非同步采样时离散频谱校正中存在的计算准确度与实时性的矛盾，本文利用三角自卷积窗所具有良好的频谱泄漏抑制特性，结合三角自卷积窗的频谱函数，采用最小二乘法建立谐波参数求解的多项式，构建了计算简便、易于实现的谐波幅值、频率、初相角参数计算式。在实际使用中，可根据不同精度要求选择拟合多项式，因此该方法具有可调节、实时性高、易于嵌入式系统实现的优点。对存在白噪声和基波频率波动等情况的谐波参数仿真分析结果表明，本文算法能有效克服白噪声、基波频率波动的影响，实现高准确度的谐波参数分析，具有一定的实用价值和参考意义。

[1]Chang G W,Chen C I,Liu Y J,et al.Measuring power system harmonics and interharmonics by an improved fast Fourier transform-based algorithm[J].IET Generation,Transmission & Distribution,2008,2(2): 193-201.

[2]Hagh M T,Taghizadeh H,Razi K.Harmonic minimization in multilevel inverters using modified species-based particle swarm optimization[J].IEEE Transactions on Power Electric,2010,24(10): 2259-2267.

[3]蔡涛,段善旭,刘方锐.基于实值MUSIC算法的电力谐波分析方法[J].电工技术学报,2009,24(12):149-155.Cai Tao,Duan Shanxu,Liu Fangrui.Power harmonic analysis based on real-valued spectral MUSIC algorithm[J].Transactions of China Electrotechnical Society,2009,24(12): 149-155.

[4]Yang Rengang,Xue Hui.A novel algorithm for accurate frequency measurement using transformed consecutive points of DFT[J].IEEE Transactions on Power Systems,2008,23(3): 1057-1062.

[5]Ferrero A,Ottoboni R.High-accuracy Fourier analysis based on synchronous sampling techniques[J].IEEE Transactions on Instrumentation and Measurement,1992,41(6): 780-786.

[6]庞浩,李东霞,俎云霄,等.应用 FFT进行电力系统谐波分析的改进算法[J].中国电机工程学报,2003,23(6): 50-54.Pang Hao,Li Dongxia,Zu Yunxiao,et a1.An improved algorithm for harmonic analysis of power system using FFT technique[J].Proceedings of the CSEE,2003,23(6): 50-54.

[7]Chen K F,Li Y F.Combining the Hanning windowed interpolated FFT in both directions[J].Computer Physics Communications,2008,178(12): 924-928.

[8]Agrez D.Dynamics of frequency estimation in the frequency domain[J]. IEEE Transactions on Instrumentation and Measurement,2007,56(6):2111-2118.

[9]Harris F J.On the use of windows for harmonic analysis with the discrete Fourier transform[J].Proceedings of IEEE,1978,66(1): 51-83.

[10]曾博,滕召胜,高云鹏,等.基于Rife-Vincent窗的高准确度电力谐波相量计算方法[J].电工技术学报,2009,24(8): 154-159.Zeng Bo,Teng Zhaosheng,Gao Yunpeng,et al.An accurate approach for power harmonic phasor calculation based on rife-vincent window[J].Transactions of China Electrotechnical Society,2009,24(8): 154-159.

[11]Nuttall A H.Some windows with very good sidelobe behavior [J].IEEE Transactions on Acoustics Speech Signal Processing,1981,29(1): 84-91.

[12]卿柏元,滕召胜,高云鹏,等.基于 Nuttall窗双峰插值FFT的高精度电力谐波分析方法[J].中国电机工程学报,2008,28(2): 48-52.Qing Baiyuan,Teng Zhaosheng,Gao Yunpeng,et a1.An approach for electrical harmonic analysis based on Nuttall window double-spectrum-line interpolation FFT[J].Proceedings of the CSEE,2008,28(2): 48-52.

[13]张介秋,梁昌洪,陈硕圃.基于卷积窗的电力系统谐波理论分析与算法[J].中国电机工程学报,2004,24(11): 48-52.Zhang Jieqiu,Liang Changhong,Chen Yanpu.Power system harmonic theory analysis and algorithm based on convolution windows[J].Proceedings of the CSEE,2004,24(11): 48-52.

[14]黄纯,江亚群.谐波分析的加窗插值改进算法[J].中国电机工程学报,2005,25(15): 26-32.Huang Chun,Jiang Yaqun.Improved window and interpolation algorithm for analysis of power system harmonics[J].Proceedings of the CSEE,2005,25(15):26-32.

[15]温和,滕召胜,王一,等.基于三角自卷积窗的介损角高精度测量算法[J].电工技术学报,2009,24(2): 164-169.Wen He,Teng Zhaosheng,Wang Yi,et al.High accuracy dielectric loss angle measurement algorithm based on triangular self-convolution window[J].Transactions of China Electrotechnical Society,2009,24(2): 164-169.

[16]Wen H,Teng Z S,Guo S Y,et al.Triangular self-convolution window with desirable sidelobe behaviors for harmonic analysis of power system[J].IEEE Transactions on Instrumentation and Measurement,2010,59(3): 543-552.

[17]Courses E,Surveys T.Dynamics of frequency estimation in the frequency domain[J].IEEE Transactions on Instrumentation and Measurement,2007,56(6): 2111-2118.

[18]Antoni J,Schoukens J.A comprehensive study of the bias and variance of frequency-response-function measurements: optimal window selection and overlapping strategies[J].Automatica,2007,43(10):1723-1736.

[19]Agre D.Interpolation in the frequency domain to improve phase measurement[J].Measurement,2008,41(2): 151-159.

[20]Belega D,Dallet D.Amplitude estimation by a multipoint interpolated DFT approach [J].IEEE Transactions on Instrumentation and Measurment,2009,58(5): 1316-1323.