基于完全电压补偿法的SMES用于抑制电压暂降的参数设计

宋旭东 向铁元

（武汉大学电气工程学院 武汉 430072）

1 引言

根据相关科研机构的调研统计发现，电压暂降是发生频率最高、影响程度最严重、造成经济损失最大的一类动态电能质量问题[1-3]，其引起的用户投诉占整个电能质量问题的 80%以上[4]。目前，电压暂降已经成为最重要的电能质量问题之一。

电压暂降是指由于系统故障或干扰造成用户电压和电流持续时间0.5周波至1min内下降到额定电压或电流的 10%～90%。即幅值为 0.1（pu）～0.9（pu）（标幺值）时系统频率仍为标称值，然后又恢复到正常水平。电压暂降可能造成某些用户的生产停顿或次品率增加，而供电恢复时间取决于自动重合闸或自动功能转换装置的动作时间，因此传统的机械式断路器已不能满足敏感和严格用电负荷的需要。目前，主要解决的方案有利用高速固态切换开关SSTS、动态电压恢复器DVR或利用不间断电源UPS作为后备电源并配合固态电子开关等[5]。

超导磁储能系统（SMES）是将超导磁体与电力电子变换装置相结合用于电力系统的一种新型电力调节装置，是超导电力技术应用领域中一个很重要的方面。由于SMES利用电力电子装置与电力系统相连，不仅可以实现对SMES输入输出功率的四象限调节，而且还能够控制能量在SMES和电力系统之间的双向流动，并具有极快的能量交换响应速度，因此，SMES能够主动抑制电压暂降，有效地改善电能质量。

超导磁体将电能转换为磁场能并无损耗地储存起来。从理论上来说，随着磁体电流的增加，超导磁体可以无限储能。但是，由于磁体的制造工艺以及其固有的电磁特性，当磁体电流超过临界电流时，磁体就会失超。因此，在研究SMES用于抑制电压暂降并进行相应的仿真实验时，将磁体中初始电流设置为较大值是没有意义的。本文在采用SMES对电压暂降进行完全电压补偿时，结合SMES的功率交换范围以及超导磁体的电流特性，提出磁体初始电流参数以及相应参数的设置规则，解决在进行SMES仿真研究时，参数设置的盲目性，并利用PSCAD/EMTDC建立全时域仿真模型，证明所提出的参数设置规则的合理性和实用性。

2 抑制电压暂降的完全电压补偿法

目前，关于抑制电压暂降，补偿电压的控制策略主要有三种方法：完全电压补偿、最小电压补偿法和最小能量补偿法[6]。三种补偿方法如图1所示。

图1 抑制电压暂降的三种策略Fig.1 Three strategies for suppressing voltage sag

如图1a所示，完全电压补偿法是指补偿后的电压完全恢复到电压暂降发生前的负荷电压水平。这种前-故障补偿策略能够保持电压幅值和波形的连续性，对于负荷侧而言，尤其对电能质量要求严格的负荷来说，是最佳的补偿策略。因此，本文采用完全电压补偿作为SMES的控制策略，来深入研究SMES的参数设计。

3 超导磁体的电磁特性

超导磁体的负荷线如图2所示。

图2 超导磁体的负荷线Fig.2 Load curve of the SM

图2中，直线I(H) 为磁体的负荷线；虚线Ic(H)表示超导导线在不同强度磁场下的临界电流值，它与负荷线的交点 c是该磁体的临界点，电流超过Ic(Hc) 磁体就会失超。负荷率越低，磁体的安全裕度就越大[7]。因此，将 SMES应用于电力系统，提高系统稳定性，改善电能质量时，如何设计超导磁体中的初始电流显得尤为重要。换言之，本文研究SMES多大的储能可以解决多大的问题。

4 基于完全电压补偿法的SMES抑制电压暂降时初始参数的设计

SMES的初始参数包括超导线圈的电感值 L、线圈起磁后的初始电流Ism_ref。SMES根据拓扑结构的不同分为电流源型SMES（CSMES）和电压源型SMES（VSMES），对于VSMES而言，其初始参数还包括支撑电容电压Udc。

4.1 超导线圈L的选取规则

超导储能系统的核心即超导线圈，是超导储能装置中的储能元件，可以等效为没有电阻的纯电感元件L，其储存的能量可表示为

由式（1）可知，当L确定后为常数时，I的大小直接决定了超导线圈的储能大小。但是超导磁体的载流能力又受制于自身临界电流Ic(Hc) 以及磁体本身承受的直流电压 USMES。

考虑以上因素并结合实际已经研制出的 SMES装置，本文中将L设置为10H。

4.2 初始电流Ism_ref的选取规则

忽略电子器件的损耗，Ism_ref直接反应了SMES抑制电压暂降的最小储能Eref。Eref主要包括了以下两部分能量：SMES抑制电压暂降的输出能量ΔE和保证SMES最小功率调节范围的储能E0，即

根据式（1）和式（3）即可得到初始电流Ism_ref为

此外，考虑到超导磁体本身的电磁特性，则Ism_ref必须满足

4.2.1 SMES抑制电压暂降的输出能量ΔE

Ism_ref的设置是为了保证 SMES能够在电压暂降的故障期间持续提供能量，保持负荷侧的电压幅值和相位为故障前的状态值不变。假设故障前负荷电压Vload、负荷电流Iload、系统电压 Vs，故障后系统电压Vsag分别为

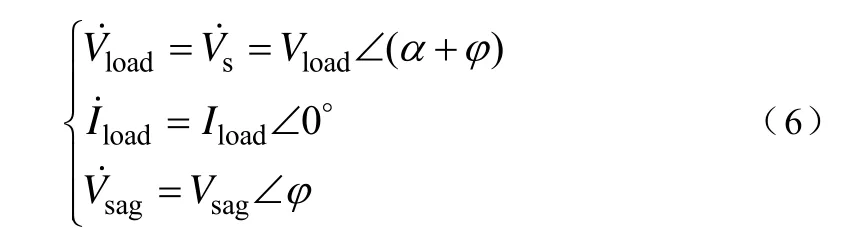
本文研究基于完全电压补偿法来抑制电压暂降。因此，根据图1a所示的相量关系，有

由式（6）和式（7）可以得到补偿电压的幅值Vcomp和相角δ 分别为

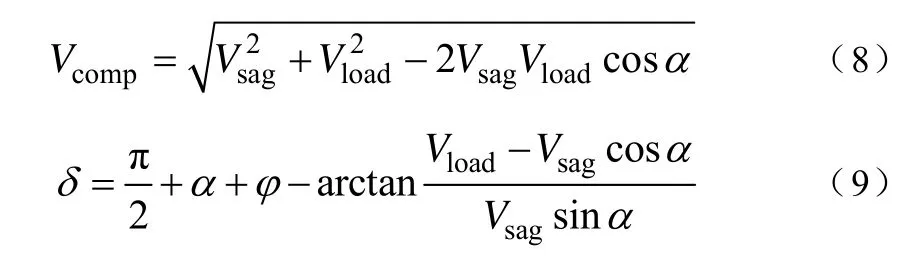
由式（6）、式（8）和式（9）可以得到 SMES在电压暂降故障期间所需要提供的有功功率ΔP、无功功率ΔQ和能量ΔE分别为

式中，tsag为电压暂降时间。

4.2.2 SMES最小功率调制范围的储存能量E0

E0是为了保证SMES在故障结束的瞬间（磁体电流最小）仍然能够保持功率调节范围正好覆盖功率点（ΔP，ΔQ）。由于 VSMES的功率调节范围与超导磁体的储能无关，因此E0VSMES=0，此处只讨论CSMES的最小功率调节储能E0CSMES。CSMES的功率调节范围如图3所示，其一相等效电路如图4所示。

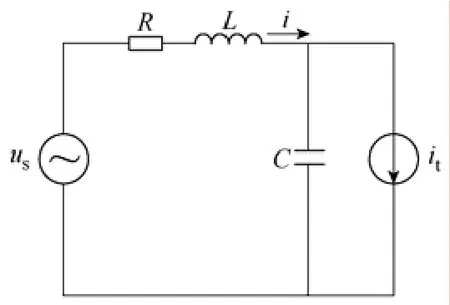
图4 CSMES一相等效电路Fig.4 One-phase equivalent circuit of CSMES

图3中，O为 CSMES功率圆的圆心坐标；R为最小功率调节范围时的半径；Rref为初始时CSMES的最大功率调节范围的半径。随着CSMES释放能量，功率圆将缩小，功率调节半径也逐渐缩小。当系统故障结束时，半径由初始时的Rref缩小为R。

功率圆圆心坐标O和功率圆半径R如下：

式中，Us为系统电压幅值；XL、XC分别为 CSMES系统中一相等效电路（见图 4）的滤波电感和缓冲电容；It为CSMES交流侧输出电流幅值；M为调制比，与调制方式相关；Idc为磁体直流电流。

因此，E0CSMES可以根据式（10）、式（11）和式（13）得到，即

4.3 VSMES支撑电容电压Udc的选取规则

VSMES的支撑电容电压 Udc的选取涉及到VSMES的功率调节范围，在电路结构确定的前提下，Udc的大小与功率调节范围成正比。VSMES的功率调节范围如图5所示，其一相等效电路如图6所示。

图5 VSMES的功率调节范围Fig.5 Power regulation range of VSMES

图6 VSMES一相等效电路Fig.6 One-phase equivalent circuit of VSMES

图5中，O为 VSMES功率圆的圆心坐标；R为最小功率调节范围时的半径。VSMES通过电压源型逆变器VSC调节输出功率，而超导磁体L则释放能量维持支撑电容两端的直流电压 Udc恒定不变。同时，由于Udc直接决定R的大小，因此，在整个抑制电压暂降的过程中，VSMES的功率调节范围不变，即功率圆不变。

功率圆圆心坐标O和功率圆半径R为

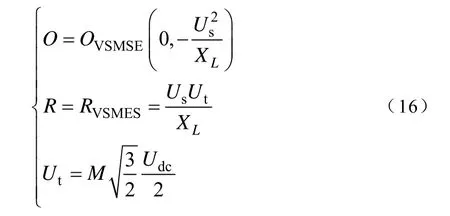
式中，XL为VSMES系统中一相等效电路（见图6）的滤波电感感抗；Ut为 VSMES交流侧的输出电压幅值；M为调制比。

因此，根据式（10）、式（11）和式（14）可得Udc为

4.4 初始参数的修正

在考虑到电子器件等其他损耗时，超导磁体的起磁电流 Ism_ref需要适当增大，以弥补损耗引起的能量损失。

同时，在电压暂降故障发生时系统电压幅值会减小，直接影响到SMES接入点的电压，导致SMES功率圆的圆心O上移和半径R减小，使得SMES的功率调节范围减小，可能导致无法输出有功功率ΔP和无功功率ΔQ。而CSMES功率圆的半径可调参数只有It，VSMES功率圆的半径可调参数只有Ut，因此，对于 CSMES而言，需要调整 Ism_ref以保证CSMES开始动作瞬间能发出所需功率；对于VSMES而言，需要调整Udc以确保VSMES开始动作瞬间能发出所需功率。

5 仿真分析

本文利用PSCAD/EMTDC软件建立了CSMES和 VSMES的全时域仿真模型，采用本文提出的参数设计规则设置相应的初始参数，并分别通过CSMES和VSMES抑制电压暂降的仿真验证上述规则的合理性和实用性。

5.1 仿真系统说明

利用SMES抑制系统电压暂降的电路图如图7所示。图7中，VSMES模块为电压源型超导磁储能装置，此时研究VSMES的参数设置；当研究CSMES的参数时，则将VSMES模块替换成CSMES模块。该仿真系统中，系统电源是线电压为 380V、频率50Hz的理想三相对称电源；系统运行到18s时发生了 0.75s的三相接地短路故障。在系统发生故障的0.75s中，重要负荷处线电压 Vload跌落 50%；故障恢复后，Vload恢复为正常值。

图7 利用VSMES抑制系统电压暂降的电路图Fig.7 The circuit diagram of VSMES for compensating the voltage sag

按照补偿方式的不同，DVR主要可以分为两大类：相电压补偿型和线电压补偿型。相电压补偿型DVR具有控制方便、可补偿零序电压等特点，适合用于包括不平衡故障在内的各种电网电能质量问题，但是存在功率器件多、体积大、造价高等问题；而线电压补偿型DVR所需功率器件少、结构紧凑，适合处理仅要求线电压不偏离标称值的电能质量问题[7]。此外，许多三相负载为无中性线的对称负载。因此，结合仿真算例的故障类型，本文采用线电压补偿型DVR，其变流器单元采用三相三线制的半桥变流器结构，如图8所示。

图8 基于VSMES的DVR的主电路图Fig.8 Main circuit diagram of DVR based on VSMES

5.2 SMES初始参数设计分析

根据图1a及图7中的系统参数可得，在系统没有接入SMES时，系统电路图如图9所示。

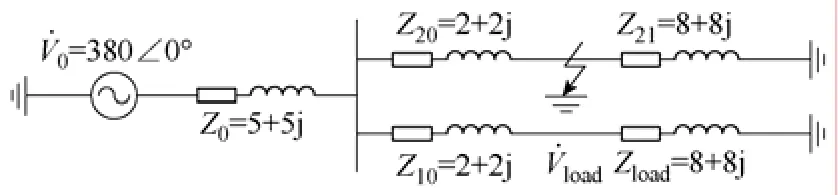
图9 未接入SMES时系统电路图Fig.9 The circuit diagram of power system without SMES

根据本文所提出的SMES参数设计规则，以及仿真系统的相关数据，可以得到SMES的初始参数如下：超导线圈 L=10H；CSMES的初始电流Ism_ref=50A；VSMES的初始电流Ism_ref= 30A，支撑电容电压Udc=100V。

5.3 仿真结果研究

VSMES抑制电压暂降的仿真波形如图 10～图12所示。

图10中，曲线V0是系统未接入SMES时，系统的重要负荷处电压的标幺值；V是系统接入VSMES后，系统的重要负荷处电压的标幺值。由此看出，VSMES较好地抑制了系统的电压暂降，保持了重要负荷处的电压。

图10 VSMES补偿电压暂降电压对比图Fig.10 Comparison graph of the generatrix voltage

图11 VSMES中支撑电容电压Udc的曲线Fig.11 The voltage of the support capacitance

图12 VSMES中超导磁体电流ISMES的曲线Fig.12 The superconducting magnet current

由图11和图12可见，在VSMES能够抑制电压暂降的前提下，VSMES的参数选取是合适的，即VSMES的参数设计规则是合理的。

CSMES抑制电压暂降的效果与 VSMES的类似，且在最终效果的验证下，其参数设计也是合适的，可行的。因此，CSMES的参数设计规则也被证明是合理的。

综上所述，基于完全电压补偿法利用SMES抑制电压暂降，保护重要负荷时，SMES的参数设计规则具有可行性和实用性。需要注意的是，该规则并非局限于SMES抑制电压暂降，SMES在电力系统中的其他应用仍可以参考该规则设计初始参数。

6 结论

本文在分析SMES功率特性的基础上，采用完全电压补偿法抑制重要负荷处的电压暂降时，提出了 SMES的初始参数设计规则；并利用 PSCAD/EMTDC软件建立了 SMES模型，对所提出的参数设计规则做了仿真验证，结论如下：

（1）SMES具有快速的四象限调节能力，能够有效地抑制电压暂降。

（2）所提出的初始参数设计规则是合理的，为SMES的参数设计提供了有益的参考。

（3）在设计磁体电流时，需要留有一定的裕度，避免出现磁体电流过小，影响SMES效果。

（4）SMES抑制电压暂降时，电压暂降的检测方法、SMES的控制策略以及谐波问题都会影响最终的补偿效果，需要进一步的深入研究。

[1]肖湘宁.电能质量分析与控制[M].北京：中国电力出版社,2004.

[2]Lamoree J,Mueller D,Vinett P,et al.Voltage sag analysis case studies[J].IEEE Transactions on Industry Applications,1994,30(4): 1083-1089.

[3]McGranaghan M F,Mueller D R,Samotyi M J.Voltage sags in industrial systems[J].IEEE Transactions on Industry Applications,1993,29(2):397-403.

[4]Hingoran N G.Introducing custom power[J].IEEE Spectrum,1995,32(6): 41-48.

[5]董其国.电能质量技术问答[M].北京: 中国电力出版社,2003.

[6]杨晓萍,许辉,吴成林.动态电压恢复器电压补偿策略及其仿真研究[J].电工技术杂志,2004,23(9):58-61.Yang Xiaoping,Xu Hui,Wu Chenglin.Voltage compensation strategies and simulation of dynamic voltage restorer[J].Electrotechnical Journal,2004,23(9): 58-61.

[7]唐跃进,石晶,任丽.超导磁储能系统(SMES) 及其在电力系统中的应用[M].北京：中国电力出版社,2009.

[8]李学斌,赵彩宏,黄晓华,等.基于超导储能系统的电网电压快速补偿算法[J].电网技术,2006,30(22): 95-98.Li Xuebin,Zhao Caihong,Huang Xiaohua,et al.A fast algorithm for single-phase voltage compensation based on superconductive magnetic energy storagesystem[J].Power System Technology,2006,30 (22):95-98.

[9]Song Xudong,Xiang Tieyuan,Peng Xiaotao.The time domain simulation of the voltage source converter fed SMES in power system[C].APPEEC 2009-Proceedings,2009.

[10]Carson W Taylor.Power system voltage stability [M].New York: McGraw-Hill,1994.

[11]金建勋.高温超导体及其强电应用技术[M].北京：冶金工业出版社,2009.

[12]刘逊,朱晓光,褚旭,等.基于超导储能的瞬时电压跌落补偿[J].电力系统自动化,2004,28(3):40-45.Liu Xun,Zhu Xiaoguang,Chu Xu,et al.Voltage sag compensation by SMES[J].Automation of Electric Power Systems,2004,28(3): 40-45.

[13]林继如,尹忠东,颜全清.基于超导储能的动态电压恢复器的研究[J].高电压技术,2008,34(3):609-611,614.Lin Jiru,Yin Zhongdong,Yan Quanqing.Research on superconducting magnetic energy storage based on dynamic voltage restorer[J].High Voltage Engineering,2008,34(3): 609-611,614.

[14]冯小明,杨仁刚.动态电压恢复器电压补偿策略的研究[J].电力系统自动化,2004,28(6): 68-72.Feng Xiaoming,Yang Rengang.Analysis of voltage compensation strategies for dynamic voltage restorer(DVR)[J].Automation of Electric Power Systems,2004,28(6): 68-72.

[15]郭文勇,张志丰,肖立业.基于共直流电压母线级联型超导储能系统的动态电压恢复器最小能量控制[J].电网技术,2009,33(5): 69-74.Guo Wenyong,Zhang Zhifeng,Xiao Liye.Minimum energy control of dynamic voltage restorer based on common DC voltage link cascaded supercon- ducting magnetic energy storage system[J].Power System Technology,2009,33(5): 69-74.