基于JPEG2000的电能质量扰动数据压缩方法

张 明 李开成 胡益胜

（华中科技大学电气与电子工程学院 武汉 430074）

1 引言

随着电力系统对电能质量分析需求的提高和硬件技术的发展，电能质量信号采集的站点数、采样精度和采样时间随之增加，需要存储和传输的电能质量数据量迅速增长，由于数据量庞大，数据以原始的形式长期保存下来是不现实的，这样对电能质量数据进行压缩是十分必要的[1]。电能质量信号自身具有一定的冗余度，使用压缩的方法可以减少这些冗余，不仅可以节省存储空间，同时也可以有效减少电能质量数据传输对带宽的占用。

目前，小波（包）变换在解决电能质量扰动数据压缩问题上的有效性已经得到证实[2-10]。用一维（1-Dimensional,1-D）小波（包）进行扰动数据压缩时，通过将信号分解为多个尺度，在每个尺度上，将对应的小波系数进行阈值量化处理，保存与扰动相关的小波系数值而抛弃其他与扰动无关的小波系数值，从而实现压缩。对小波系数进行处理时，如阈值选取过大则信号压缩率高，但有效信息损失较大；如阈值选取过小则信号压缩率过小，两者存在着矛盾。为了提高1-D小波的压缩效率，文献[11]基于优化小波基，文献[12]基于多小波，文献[13-14]使用提升小波算法，这些方法使压缩性能进一步得到了提高。

但是现有1-D信号压缩理论与技术难以兼顾压缩效率与信号质量的提高，一些学者开始考虑用二维（2-Dimensional,2-D）或图像压缩技术对1-D电能质量信号进行压缩处理，如Gerek等人将2-D小波压缩技术用于电能质量数据压缩，实验结果显示其压缩性能优于1-D小波压缩方法[15-16]，赵艳粉等人的实验结果也证明了2-D小波电能质量数据压缩性能好于1-D小波包压缩方法[17-18]，高培生等人采用图像压缩中的嵌入式零树小波编码技术进行电能质量数据压缩也获得了较好的压缩性能[19]。

基于小波变换的压缩方法主要包含三个步骤：变换、量化与熵编码。首先，原始采样数据通过小波变换产生一组小波系数并进行相应的阈值处理，然后，小波系数被量化产生符号流，符号流中的每一个符号对应量化表中的一个指标，实际上大部分的信息损失都发生在量化阶段。接着，熵编码对字符串作有效地无损表示。最后，输出编码后的比特流。可见上述基于小波变换的电能质量数据压缩方法大多仅讨论变换阶段的处理方法，而未涉及量化和编码过程对压缩的影响。并且相对而言，目前1-D信号压缩的理论与实践都远远滞后于2-D或图像压缩，可见将2-D或图像压缩方法移植到1-D数据压缩将是一个有益的探索。其中 Bilgin等人用JPEG2000压缩 1-D ECG（心电图）数据就是比较成功的范例[20]。为此，本文提出了一种基于JPEG2000的电能质量扰动数据压缩方法，其优良的压缩性能在实验中得到了验证。

2 JPEG2000简介

JPEG2000是最新的图像压缩标准，基于 2-D小波变换，采用当前最新的优化嵌入式编码技术，在获得优于目前 JPEG（Joint Photographic Experts Group）压缩的同时，生成的码流具有较强的功能，在低比特率的情况下，能获得比目前 JPEG压缩更好的率失真（Rate-distortion）性能和主观图像质量。JPEG2000压缩具有以下主要特点：

（1）良好的低比特率压缩性能：在大压缩比（编码压缩率低于0.25位/样本）情况下，JPEG2000具有良好的率失真性能，可适应网络、移动通信等有限带宽的应用需要。

（2）有损和无损压缩：在JPEG2000压缩中，通过选择参数，能够对图像进行有损和无损两种压缩，其中可逆的（5,3）小波用于无损压缩，而不可逆的（9,7）小波用于有损压缩。

（3）按照像素精度或者分辨率进行累进式传输：累进式图像传输允许图像按照所需的分辨率或像素精度进行重构，用户根据需要，对图像传输进行控制，在获得所需的图像分辨率或质量要求后，便可终止解码，而不必接收整个图像压缩码流。

（4）随机获取和处理码流：由于JPEG2000采用小波技术，利用其局部分辨特性，在不解压的情况下，可对压缩的图像数据进行传输、滤波等操作。

（5）固定速率、固定大小、有限的存储空间：JPEG2000使用分块技术，对每个小块进行处理，可以解决硬件实现以及带宽资源和存储空间有限带来的应用问题。

JPEG2000编解码器框图如图 1所示，在编码时，首先需要把源图像数据无重叠地划分成片（tile）矩形单元，将每个 tile看成是小的源图像，当然也可把整幅图像作为一个 tile，然后进行离散小波变换，根据变换后的小波系数特点进行量化，将量化后的小波系数针对每个码块进行独立的嵌入式编码，得到所有码块的嵌入式位流，按照率失真最优原则分层组织，形成不同质量的层。对每一层，按照一定的码流格式打包输出压缩码流。

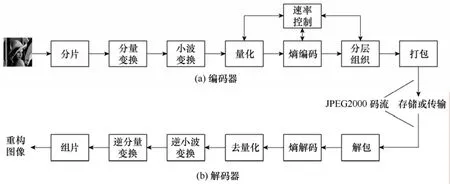
图1 JPEG2000编解码器框图Fig.1 Block diagrams of the JPEG2000 codec

解码过程相对比较简单。根据压缩码流中存储的参数，对应于编码器的各部分，进行逆向操作，输出重构的图像数据。更为详细的 JPEG2000介绍可参考文献[21]。

3 基于JPEG2000的电能质量扰动数据压缩

电能质量信号是一种准周期信号，其波形呈现某种相似性，因而是一种冗余度较大、而信息熵较小的信号，从理论上来讲，应该具有较大的压缩比。以往的1-D压缩方法大都没有考虑到这种周期间相似性冗余，因而压缩比受到很大的限制，而使用2-D压缩方法可以消除周期之间的空间冗余。本文基于JPEG2000编解码器压缩电能质量扰动数据的流程图如图2所示，主要是将电能质量信号按基频周期分段组成2-D矩阵，用电能质量信号幅度值表示为图像的灰度值。

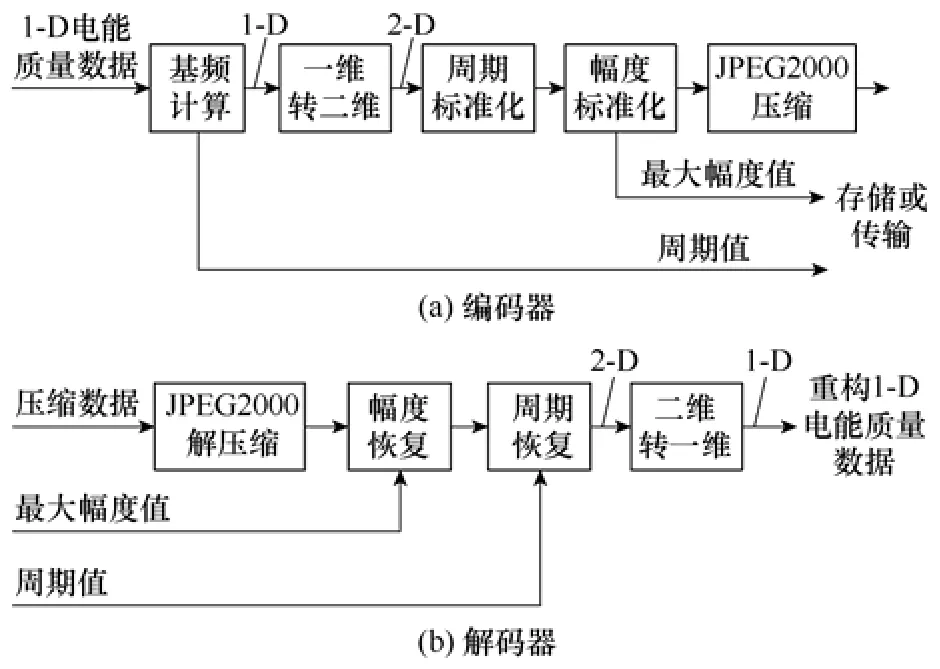
图2 基于JPEG2000的压缩方法流程图Fig.2 Block diagrams of the proposed method using JPEG2000

为了充分利用周期间的相关性，需要对1-D电能质量信号进行基频计算，并依据计算结果对原始1-D电能质量信号进行分割和排列，文献[22]通过对比现有多种典型的基频计算算法，如快速傅里叶变换（Fast Fourier Transform,FFT），插值 FFT（Interpolated FFT,IpDFT），Chirp-Z变换，自适应 Kalman滤波，小波，短时傅里叶变换，Hilbert变换，最小二乘方正弦拟合（Least-squares Sinefitting），以及多重信号分类算法（Multiple Signal Classification），实验结果表明在噪声和谐波背景下，IpDFT算法在计算精度、速度等方面优于其他几种算法，而且在分析基频变化的电能质量波形方面具有一定的适应性。为此本文采用该算法。

图3给出了1-D电能质量信号经过基频计算得到周期后，被分割和排列成2-D电能质量信号矩阵的过程。将1-D电能质量信号按周期分段，逐行排列，这样周期之间的相似性映射到二维图像相邻行之间的相似性，一周期内部采样点之间的变化趋势映射到二维图像相邻列之中，例如有一256个周期，每周期 256个采样点的电压骤降信号（第 10～40周期发生骤降），图4a为其2-D图像，并对其进行1尺度2-D离散小波变换（采用Daubechies4小波），如图4b所示，图中LL表示低频子带，保持了原始图像的内容信息，图像的能量集中于此频带；HL表示垂直子带，保持了图像水平方向上的高频边缘信息；LH表示水平子带，保持了图像竖直方向上的高频边缘信息；HH表示高频子带，保持了图像在对角线方向上的高频信息。

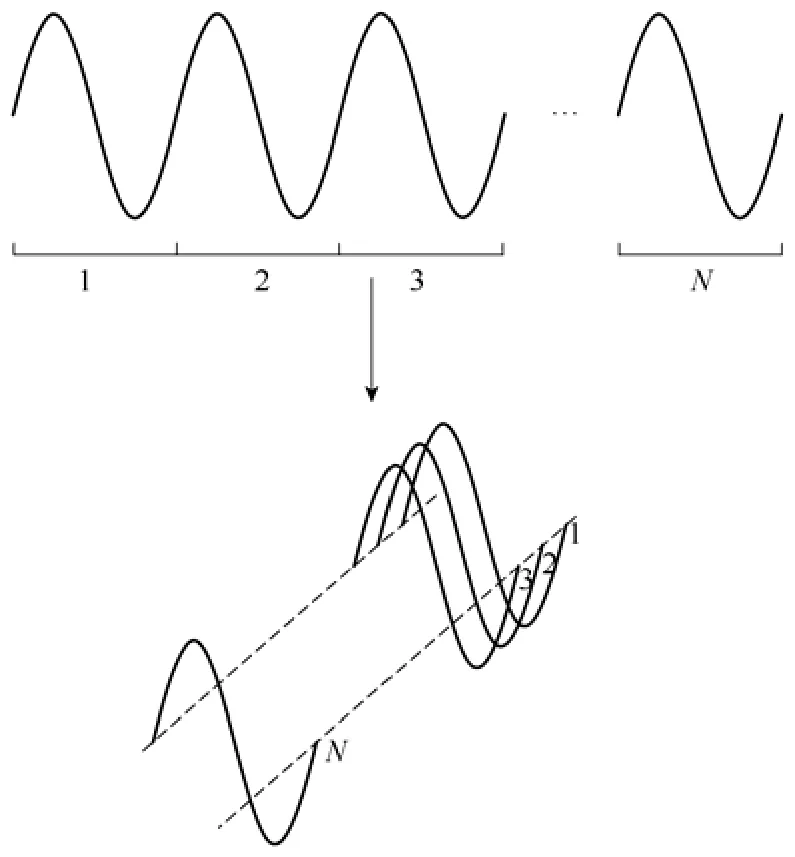
图3 1-D数据变2-D矩阵（或图像）Fig.3 2-D matrix (or image) generation from 1-D data

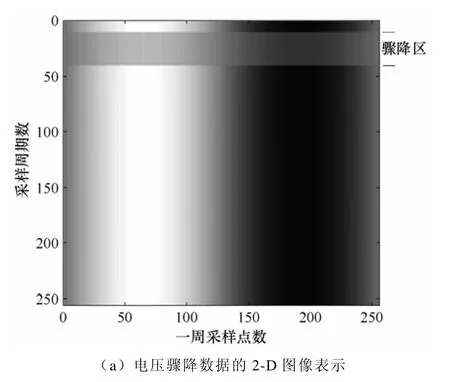
图4 电压骤降数据的二维图像表示及其1尺度2-D小波分解Fig.4 2-D image expression of voltage sag data and its 1-level 2-D wavelet decomposition

因此，可以将2-D图像的压缩方法，应用到1-D电能质量信号的压缩上来，同时基频值也被传输或存储。周期标准化是为使各段长度相同，本文方法允许在各电能质量序列段后添加适当数目的 0。由于基频值已经被编码了，因此不需要再对补零的个数进行传输或存储。

幅度标准化可以使电能质量数据之间的相关性增强。将各电能质量序列采样值分别除以本段数据的最大值，从而使各段电能质量数据的最大幅值等于 1。这样，各段之间的幅度差异将减小，从而增强了数据之间的相关性。同时最大幅度值也将被传输或存储。

为了重建电能质量信号波形，要求压缩数据包括以下信息：①基频值与最大幅度值；②小波系数的编码码流。重建过程如图2b所示。

4 实验结果及讨论

4.1 压缩效果评价指标

为了对数据压缩方法进行性能评估，定义了如下衡量指标：

（1）压缩比（Compression Ratio，CR）

式中，Scompressed为压缩后信号数据大小；Soriginal为原始数据大小。

（2）在信号的压缩处理中，通常采用均方误差百分值（Percent of Root-mean-square Difference in Percentage，PRD）来评估其压缩性能[20]，则 PRD的计算式为

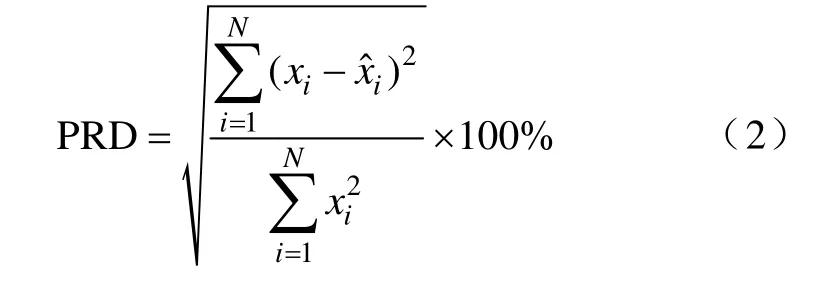
式中，i为信号点的位置；N为信号长度；xi为第i个点原始信号值；xˆi为第i个点经过压缩处理后重构的值。

4.2 实验结果与分析

以实际电网中采集得到的不同类型电能质量扰动信号作为实验对象[25]，来测试 JPEG2000的压缩性能。这些信号的幅值取标幺值，采样频率为12.8kHz，每组信号长度为256个周期（5.12s，50Hz系统），以每个周期256个采样点作为2-D矩阵的一行即可构成一个 256×2562-D矩阵。通常可用二进制数字有限的精度来代表实数，即所有的实数都可以用一串二进制数字来表示，二进制数字表达式的右端每添加一位长，都会取得更好的精度。这样，在允许的精度误差内，可以取有限的位长来表示信号的幅值。由此为了验证方便，本文实验中将原始数据统一保存为无压缩的8位灰度位图格式（8位/样本）。

本文实验采用在 Matlab7.0中调用软件Kakadu6.2.1[26]来实现JPEG2000编解码器，并且能通过参数的设置实现不同 CR的压缩，同时将基频值与最大幅度值嵌入到公共的文件头信息中一并传输。Kakadu软件使用缺省的参数设置，如码块尺寸为64×64，采用（9,7）小波，5层小波分解，等等。实验中，首先将1-D数据变成2-D图像后，然后对其进行 JPEG2000有损压缩，生成 JPEG2000图像（*.j2c）文件，接着再对该*.j2c文件解码最后得到重构数据。

4.2.1 压缩重构性能评估

电能质量扰动信号主要分为稳态信号（如谐波）和非稳态信号（如骤降）[23]，而压缩算法性能的高低和待压缩信号本身的特性有关，为了更好地评估JPEG2000针对不同类型电能质量扰动信号的压缩性能，本文采用谐波和骤降两种典型的电能质量扰动信号来测试 JPEG2000的压缩性能，同时与 Gerek等人压缩算法[15]（以下简称 Gerek算法）进行压缩重构性能对比实验，Gerek算法采用3尺度2-D离散小波变换，而且为了保留信号特征，通过将一部分幅度较小的小波系数设为0来压缩数据，然后使用逆变换得到重构信号，同时可依据希望的 CR，来确定需要置为0的小波系数数目，例如当CR为4:1时，75%幅度较小的小波系数设为0而其余25%得到保留。实验结果如图5和图6所示。图中误差信号为原始信号与重构信号之差。从图5和图6中可以看出在同样 CR下，针对不同类型的电能质量扰动信号，JPEG2000压缩的重构误差均小于Gerek算法，可见 JPEG2000的压缩重构性能优于 Gerek算法。同时从这些图中也可以看出信号的关键特征在重构信号中得到较好的保留，无论是稳态信号和非稳态信号，JPEG2000压缩都能得到很好的压缩重构性能。

图5 JPEG2000和Gerek算法的压缩重构性能比较（谐波）Fig.5 Comparison of compression and reconstruction performance between JPEG2000 and Gerek method(harmonic)

图6 JPEG2000和Gerek算法的压缩重构性能比较（骤降）Fig.6 Comparison of compression and reconstruction performance between JPEG2000 and Gerek method (sag)

4.2.2 与其他压缩算法比较

图7 三种2-D压缩方法在不同CR下的PRD比较（谐波）Fig.7 PRD comparison of three 2-D compression methods with difference CRs (harmonic)

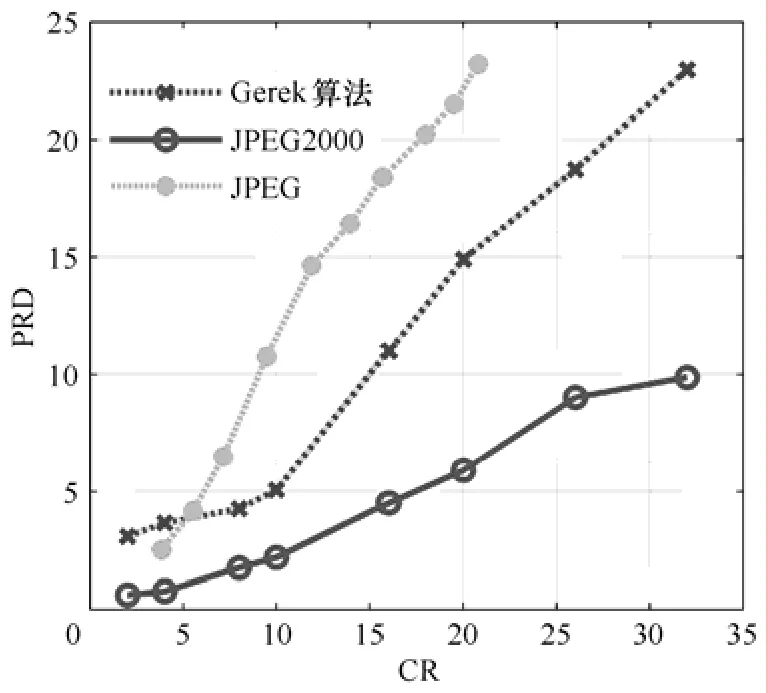
图8 三种2-D压缩方法在不同CR下的PRD比较（骤降）Fig.8 PRD comparison of three 2-D compression methods with difference CRs (sag)

为了进一步评估 JPEG2000在不同 CR下的压缩性能，使用 JPEG2000、Gerek算法及 JPEG（基于2-D离散余弦变换的分块编码方式）[24]进行压缩实验对比，采用同上的两种信号，实验得到的PRD-CR曲线如图7和图8所示。实验表明对于不同类型的电能质量扰动信号，JPEG2000压缩的PRD指标在不同 CR下都优于其他两种压缩方法，而且随着CR的增加，JPEG2000压缩算法的重构波形误差只是渐缓增加，而其他两种压缩方法当 CR较大时，其重构波形误差较大，这主要是因为JPEG2000其独特的量化编码方式，可以适应不同类型的电能质量扰动信号构成的2-D图像。而Gerek算法只是以简单的方式对小波系数进行处理，当要求 CR较大时这种处理方式会产生较大的重构波形误差；另外基于离散余弦变换的 JPEG压缩有无法消除的方块效应，在同样的 CR下，会产生比 JPEG2000大的重构波形误差。

4.2.3 渐进传输性能验证

JPEG2000编解码器对码流可以渐进解码，为了展示JPEG2000的渐进解码性能，实验采用同上的两种信号，使用 CR为2:1（4位/样本）的码流，采用在不同的CR下对码流进行解码，如图9和图10所示，结果表明 JPEG2000具有很好的渐进重构质量，直到很高的压缩比，例如 CR=80 :1（0.1位/样本），而且重构质量随着 CR的增加是渐渐降低的。这是因为首先传输的是 JPEG2000码流中的重要系数，其次是不重要系数（即对图像而言是不断地补充细节），这样即使码流中断，也可以得到一幅完整的图像，只是分辨率差些。也就是说接收端可以在任何时候停止接收编码信息，而不影响图像的解压缩和重构。因此 JPEG2000的这种渐进解码特性可以很好地适应于当前电能质量监测网网络通信的需要。

图9 不同CR下的重构信号（谐波）Fig.9 Reconstructed signals with difference CRs（harmonic）

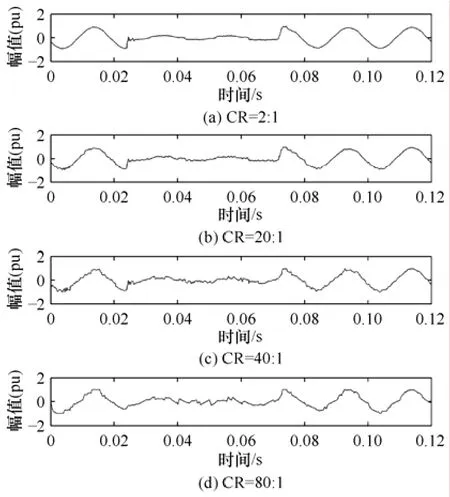
图10 不同CR下的重构信号（骤降）Fig.10 Reconstructed signals with difference CRs（sag）

4.2.4 压缩方法的实时性

为了验证 JPEG2000压缩的实时性，验证环境设置为：CPU为Pentium (R)42.66 GHz主频；内存为512 MB；操作系统为Microsoft windows XP SP2。测试数据为IEEE PES数据库中的60个记录[25]，包括各种类型的电能质量扰动信号，同样取长度 256个周期的原始电能质量扰动信号（共 256×256个采样点）进行实验。实验主要步骤包括：

变换→量化→编码→解码→去量化→逆变换CR分别取 2: 1,4: 1,8:1,16: 1,32:1,64:1，这样共240次实验，实验结果显示整个压缩及解压缩过程消耗时间在0.434260～0.487904s之间，同时对于不同类型的电能质量扰动信号和不同的 CR并没有显示出明显的差异来，可见基于 JPEG2000的压缩能满足实时性的要求（远小于5.12s），同时也能适应不同类型电能质量扰动数据的压缩。目前，DSP的运算速度已达百兆以上，因此从数量级的角度来看完全能够满足电力部门对电能质量监测网的实时性要求。

5 结论

在分析现有的电能质量扰动数据压缩算法的基础上，为了充分利用二维矩阵数据间的相关性，本文提出并设计了基于 JPEG2000的电能质量扰动数据压缩方案。利用实际获取的电能质量扰动数据对算法进行了验证，将 JPEG2000压缩方法与 Gerek算法、JPEG压缩方法进行了实验对比，结果表明JPEG2000在压缩效果上优于其他两种方法，具体体现在同样 CR下重构误差更小，能适应不同类型的电能质量扰动数据压缩，以及具有渐进传输特性。此外，在 JPEG2000压缩后的图像中，还包含了一部分公共的文件头信息，如 JPEG2000图像的层数等，如将这部分信息去除，压缩比仍有提高的空间。

JPEG2000压缩方法能满足系统实时性的要求，而且核心算法已有很成熟的硬件产品，如 Analog Device公司开发的 ADVJP2000芯片组可用于JPEG2000的编解码。因此，本文提出的JPEG2000压缩方法有可能直接应用于便携式电能质量分析仪中。同时，还可以应用于其他电力系统数据测量设备当中。

[1]Ribeiro M V,Park S H,Romano J M T,et al.A novel MDL-based compression method for power quality applications[J].IEEE Transactions on Power Delivery,2007,22(1): 27-36.

[2]Santoso S,Powers E J,Grady W M.Power quality disturbance data compression using wavelet transform methods[J].IEEE Transactions on Power Delivery,1997,12(3): 1250-1257.

[3]Hsieh C T,Huang S J,Huang C L.Data reduction of power quality disturbances – a wavelet transform approach[J].Electric Power Systems Research,1998,47(1): 79-86.

[4]Littler T B,Morrow D J.Wavelets for the analysis and compression of power system disturbances[J].IEEE Transactions on Power Delivery,1999,14(2):358-364.

[5]张兆宁,郁惟铺,张毅刚.基于小波包和矢量量化的电力系统故障数据压缩[J].电力系统自动化,2003,27(1): 45-48.Zhang Zhaoning,Yu Weiyong,Zhang Yigang.Power system fault data compression using the wavelet packet transform and vector quantification[J].Automation of Electric Power Systems,2003,27(1):45-48.

[6]欧阳森,宋政湘,陈德桂,等.基于小波原理的电能质量检测数据实时压缩方法[J].电网技术,2003,27(2): 37-40.Ouyang Sen,Song Zhengxiang,Chen Degui,et al.A wavelet theory based real-time data compression method for power quality detection[J].Power System Technology,2003,27(2): 37-40.

[7]成敬周,张举.基于小波包分析的录波数据压缩原理[J].电力自动化设备,2004,24(7): 64-56.Cheng Jingzhou,Zhang Ju.Theory of power system fault data compression based on wavelet packet[J].Automation of Electric Power Systems,2004,24(7):64-56.

[8]刘应梅,白晓民,易俗,等.基于最小极大法的电力扰动信号压缩[J].电网技术,2004,28(3): 33-37.Liu Yingmei,Bai Xiaomin,Yi Su,et al.Compression of power quality disturbance signal based on least maximum method[J].Power System Technology,2004,28(3): 33-37.

[9]郭彬彬,黄纯.基于小波包变换的电能质量扰动数据压缩[J].电力自动化设备,2005,25(11): 34-37.Guo Binbin,Huang Chun.Power quality disturbance data compression based on wavelet packet transform[J].Electric Power Automation Equipment,2005,25(11): 34-37.

[10]剧高峰,罗安.离散小波变换用于电能质量扰动数据实时压缩[J].电力系统自动化,2002,26(19): 61-63.Ju Gaofeng,Luo An.DWT application to real-time compression of power quality disturbance data[J].Automation of Electric Power Systems,2002,26(19):61-63.

[11]何正友,钱清泉,刘志刚.一种基于优化小波基的电力系统故障暂态数据压缩方法[J].中国电机工程学报,2002,22(6): 1-5.He Zhengyou,Qian Qingquan,Liu Zhigang.An electric power system fault transient data compression method based on optimal wavelet[J].Proceedings of the CSEE,2002,22(6): 1-5.

[12]刘志刚,钱清泉.基于多小波的电力系统故障暂态数据压缩研究[J].中国电机工程学报,2003,23(10):22-26.Liu Zhigang,Qian Qingquan.Compression of fault transient data in electric power system based on multiwavelet[J].Proceedings of the CSEE,2003,23(10): 22-26.

[13]闫常友,杨奇逊,刘万顺.基于提升格式的实时数据压缩和重构算法[J].中国电机工程学报,2005,25(9): 6-10.Yan Changyou,Yang Qixun,Liu Wanshun.A realtime data compression and reconstruction method based on lifting scheme[J].Proceedings of the CSEE,2005,25(9): 6-10.

[14]周瑞,鲍文,于霄,等.基于提升小波和混合熵编码的数据压缩方法[J].电力系统自动化,2007,31(22): 65-69.Zhou Rui,Bao Wen,Yu Xiao,et al.Data compression method based on lifting wavelet transform and hybrid entropy coding[J].Automation of Electric Power Systems,2007,31(22): 65-69.

[15]Gerek O N,Ece D G.2-D analysis and compression of power quality event data[J].IEEE Transactions on Power Delivery,2004,19(2): 791-798.

[16]Gerek O N,Ece D G.Compression of power quality event data using 2D representation[J].Electric Power Systems Research,2008,78(6): 1047-1052.

[17]赵艳粉,杨洪耕.二维离散小波变换在电能质量检测数据压缩中的应用[J].电力系统自动化,2006,30(15): 51-55.Zhao Yanfen,Yang Honggeng.Data compression method using 2-dimensional discrete wavelet transform for power quality detection[J].Automationof Electric Power Systems,2006,30(15): 51-55.

[18]赵艳粉,杨洪耕.改进非分离二维离散小波的数据压缩算法[J].电力自动化设备,2007,27(5): 53-57.Zhao Yanfen,Yang Honggeng.Advanced nonseparable 2-dimensional discrete wavelet transform for data compression[J].Electric Power Automation Equipment,2007,27(5): 53-57.

[19]高培生,陈新建,吴为麟,等.二维表示的电能质量故障数据压缩[J].浙江大学学报(工学版),2008,42(4): 686-690.Gao Peisheng,Chen Xinjian,Wu Weilin,et al.Compression of 2-D representation of power quality event data[J].Journal of Zhejiang University(Engineering Science),2008,42(4): 686-690.

[20]Bilgin A,Marcellin M W,Altbach M I,et al.Compression of electrocardiogram signals using JPEG2000[J].IEEE Transactions on Consumer Electronics,2003,49(4): 833-840.

[21]ISO/IEC 15444—1.Information technology—JPEG 2000 image coding system—part 1: core coding system[S].

[22]Ramos P M,Serra A C.Comparison of frequency estimation algorithms for power quality assessment[J].Measurement,2009,42 (7): 1312-1317.

[23]IEEE Std 1159—2009.IEEE recommended practice for monitoring electric power quality[S].

[24]Wallace G K.The JPEG still picture compression standard[J]. IEEE Transactions on Consumer Electronics,1992,38(1): 18-34.

[25]IEEE Power Engineering Society.IEEE PES working group P1433 power quality definitions[DB/OL].[1999-7-30].http: //grouper.ieee.org /groups/1433/.

[26]Taubman D.Kakadu SDK V6.2.1[CP/OL].[2009-7-3].http: //www.kakadusoftware.com.