τ检验在GPS后处理中对粗差的探测分析

王亦欣

(湖南省第一测绘院，湖南衡阳 421001)

1 概述

在GPS后处理中，经过三维无约束平差(最小约束平差)后，一般要对基线残差进行分析以剔除粗差。无约束平差是以独立基线向量及其方差－协方差阵为观测量。平差后一般输出基线向量各分量改正数(残差)、基线边长、方位和点位精度信息等。常用的对基线残差探测分析方法有X2检验、τ检验、环闭合差和重复基线分析等。但τ检验对粗差探测往往具有不确定性，以下笔者试对其详细分析。

2 τ检验

观测值误差是服从正态分布的随机变量，故残差/标准残差的期望是可预计的。τ检验就是用标准残差去统计测定观测值残差是否位于期望界限之内，再计算出一个阀值来检验每个标准残差。每个被检验的标准差可能有两种结果:

①τ检验通过，标准残差不大于阀值，通常表明观测值中无粗差存在。

②τ检验失败，标准残差大于阀值，应进一步查验粗差情况。

τ检验的严密公式如下:

构造统计量:

其中:

vi为第i个观测值的残差;^σ0为单位权中误差估值;qi为第i个观测值的协因数;f为自由度，等于多余观测值的个数。

那么有:

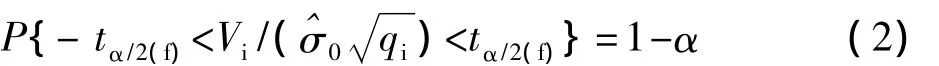
α为显著性水平。因t(f)呈对称分布，如图1所示。

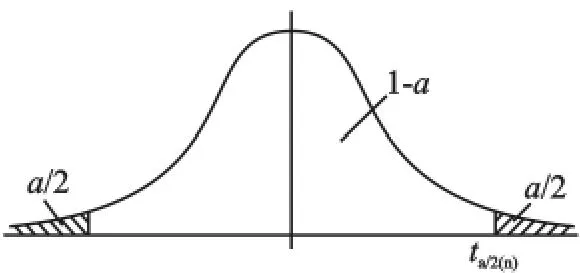
图1 τ检验置信区间图

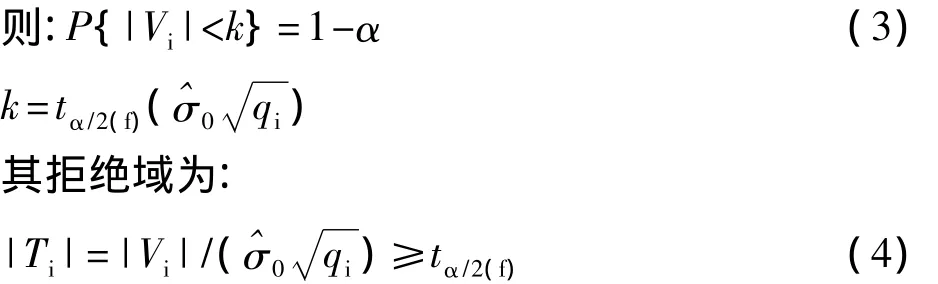
通常选择显著性水平α=0.05，置信水平为95%时，若:

(tα/2(f)可在t分布表中查得)即Vi大于其中误差的2倍时，认为与它相应的观测量含有粗差。

为了减少弃真概率，根据“3σ”原则，选择置信水平接近99.7%时，即Vi大于其中误差的3倍时，则认为其观测量含有粗差。

需要注意的是，残差未通过统计检验，并不意味着观测值中必然存在粗差，只是应进一步查验粗差情况，对可能存在粗差的基线作出标记。一个观测值的粗差往往会影响到其他观测值残差的推算。因此，这种标记可能会张冠李戴，如果有一个甚至多个观测值做上了这样的标记，可逐一检测是否真正存在粗差。

3 实例分析

以中海达Hi－TargetTMGPS数据处理软件算例进行分析。该软件实际提供的τ值为检验值与τ值的比值，如果该值小于±1.0，则说明该观测值不含粗差，如它大于±1.0，则意味着该观测值含有粗差。

例如:有GPS控制网如图2所示。

经三维无约束平差后进行τ检验，如表1所示。

表1和图3表明有3条基线含有粗差。而这3条基线向量各分量的改正数如表2所示。

τ检验列表 表1

图3中，背景曲线为理论上的τ值分布曲线，直方图为实际曲线。

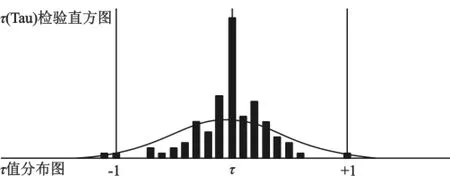
图3 τ检验直方图

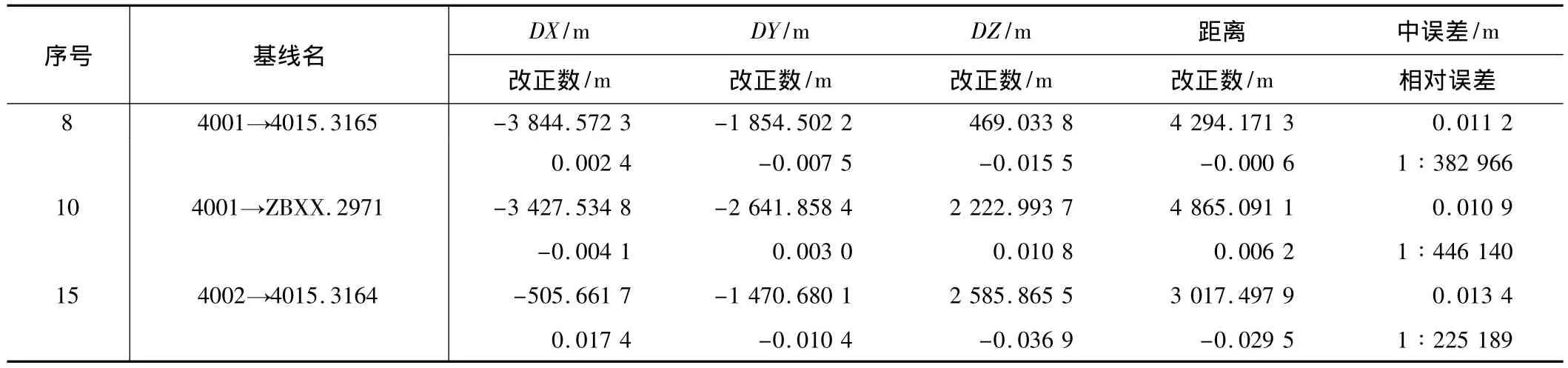
基线分量改正数 表2

对基线向量各分量的改正数可以利用以下简单公式进行检验(见《全球定位系统(GPS)测量规范》GB/T18314－2001)。

式中a为固定误差，mm;b为比例误差系数，ppm;d为相邻点间的距离，km;对 GPS E级网，取 a=10 mm，b=10 ppm。

经过计算，基线4001→4015.3165标准差 σ为4.40 cm;基线 4001→ZBXX.2971标准差 σ为4.97 cm;基线4002→4015.3164标准差 σ为3.18 cm。显而易见，上述3条基线向量各分量的改正数都远远小于各自的3σ，并不存在粗差。

接下来，我们删除4004号站点(该点离这3条基线并不近)，变成如图4所示网形。

重新平差，再进行τ检验，如表3、图5所示。

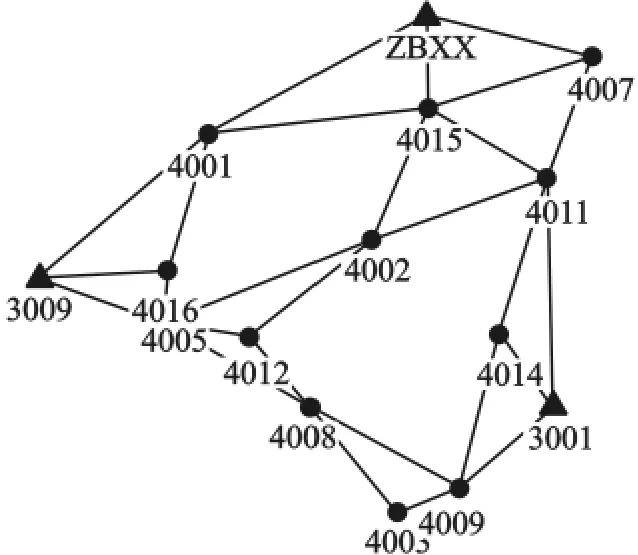
图4 改变后的GPS控制网图

τ检验列表 表3

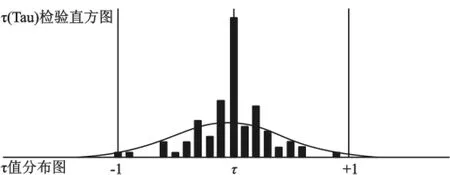
图5 τ检验直方图

结果显示，基线4001→4015.3165还含有粗差，而另外 2条基线 4001→ZBXX.2971和基线 4002→4015.3164则不再含有粗差了。观察这3条基线向量各分量的改正数与前次平差的改正数相比并没有多大的改动。如表4所示。

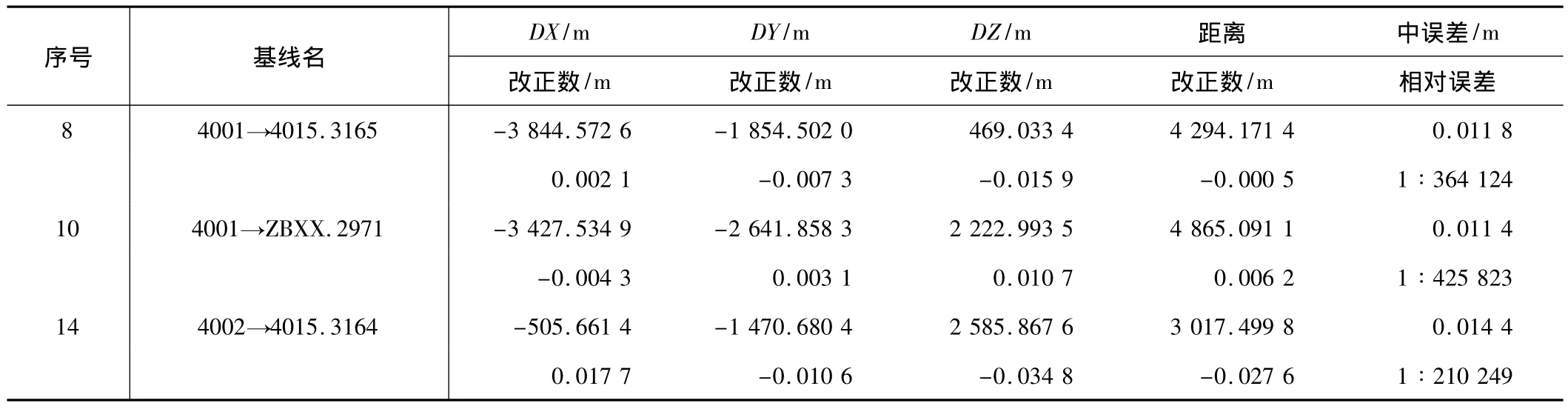
基线分量改正数 表4

4 结语

从以上的算例分析可以看出，τ检验对粗差的探测具有不确定性。如果残差τ检验通过则说明观测值不包含粗差。如果τ检验失败，粗差不一定存在，需要进一步探查。可采用最有效的粗差探测方法:独立环闭合差检验。也可采用式(6)检验，如果 V△X、V△Y、V△Z大于3σ，那么可以肯定该基线或该基线附近存在粗差，需要剔除粗差基线。因此，在 GPS网数据处理中，对平差结果的分析，过于看重τ检验的结果是没有必要的。

［1］李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2005

［2］王国祥.GPS基线解算与质量控制［J］.铁道勘察，2005(6):7～9

［3］陶本藻，姚宜斌.可靠性分析与数据探测［J］.武汉大学学报(信息科学版)，2002(6):607

［4］GB/T18314－2009.全球定位系统(GPS)测量规范［S］.

［5］盛骤，谢式千，潘承毅.概率论与数理统计［M］.北京:高等教育出版社，2008