免棱镜全站仪悬高测量法测定拱圈线形

阙名前，陈顺超

(1.云南路建集团宏程路桥工程有限公司，云南昆明 650501;2.西南林业大学交通机械与土木工程学院，云南昆明 650224)

1 引言

拱桥是我国公路上常用的一种桥梁型式，由于种种原因，大量既有拱桥已出现不同程度的病害，急需进行检测评估和维修加固。拱桥在荷载、基础变位和环境条件等因素的长期作用下，拱圈(拱肋)的轴线不可避免地要发生变化，拱轴线形状的改变又直接影响拱圈内力及截面应力的分布。因此，准确测定拱圈(拱肋)线形，是拱桥检测和评定的基础［1］。

拱圈线形测量的麻烦之处在于，人工难于抵近拱圈(拱肋)安置棱镜或水准尺，目前常用的普通全站仪直接测量法、水准仪测量法均存在这一问题，即使采用桥梁检测车，一般也仅能抵近拱顶侧面。钟正强等［2］提出的激光断面仪法，需要在拱桥的底部架设激光断面仪，由于桥下常为河流或深谷，使其应用受到限制。悬高测量是在待测目标点的天底(或天顶)安设棱镜，利用三角高程测量原理推求待测目标点高程的一种间接方法［3］。免棱镜测距技术是不需要棱镜作为合作目标就可以进行测距的一项技术，目前在全站仪中越来越普及［4］。利用免棱镜全站仪的这一优点，结合悬高测量的原理，作者在桥梁检测实践中摸索了一种测量拱圈线形的方法。

2 悬高测量法的操作程序

拱桥桥面便于安设棱镜，且桥面标高易通过水准测量精确获得，因此将棱镜置于桥面(即拱圈测点的天顶)，利用三角高程测量原理，根据桥面标高推求拱圈标高，如图1所示。具体的操作程序为:

(1)以桥面纵轴线为X轴，垂直方向为Y轴，竖向为Z轴建立局部坐标系。

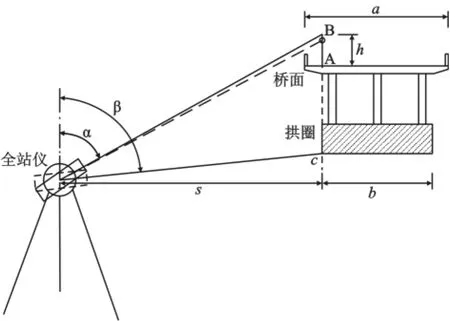
图1 悬高测量法示意图

(2)找到拱圈测点在桥面上的投影点。悬高测量的关键在于保证拱圈测点和棱镜中心在同一竖直线上。拱圈线形一般需要测量拱脚、L/8、L/4、3L/8和拱顶等特征截面。测点纵向位置可利用钢尺或全站仪精确确定。横向位置确定则要麻烦一些，分为粗定和精定两步。粗定利用拱桥的对称性完成，如图1所示，用钢尺量得桥面和拱圈宽度分别为a和b，然后从桥面边缘量距(a－b)/2初定测点A'，由于桥梁并非绝对对称，A'在横向与拱圈测点投影A仍可能存在偏差。如图2所示，立棱镜于A'点，在拱桥侧面适当位置架设免棱镜全站仪，瞄准棱镜，测出平距为L'，然后保持仪器水平制动，向下转动望远镜，瞄准拱圈侧面，利用免棱镜测距功能测出平距为L，两者差值为△L，沿箭头方向移动△L·cosM，重新立棱镜，重复上述步骤，直到L'=L，则该点为拱圈测点在桥面的投影A。

图2 拱圈测点桥面投影精定平面示意图

(3)采用水准测量测得桥面点A的高程Z0。

(4)在河流两侧适当位置架设全站仪，在桥面测点A安置棱镜，棱镜上安设照准用的觇板，用钢尺量出觇板顶部距测点的垂直距离h。

(5)测出测站点至桥面测点A的平距S，如图1所示，然后向上转动望远镜，照准觇板顶缘B，测得竖直角为α，保持全站仪水平制动，向下转动望远镜瞄准拱圈下缘C，测得竖直角为β，假设桥面测点和拱圈下缘点在同一条铅垂线上，则C点高程为:

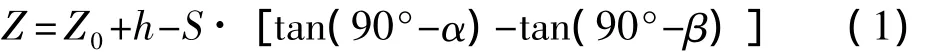
(6)将全站仪倒镜，重复步骤(5)，再次得到C点高程，两次测量取平均值作为C点Z坐标。

对于拱圈线形，拱圈下缘X、Y坐标即为桥面测点的X、Y坐标，Z坐标通过上述方法得到。下面以徕卡TCR802全站仪为例，对Z坐标的测量精度进行分析。

3 Z坐标的测量精度分析

3.1 测量误差来源

式(1)默认桥面测点与拱圈下缘点在同一铅垂线上，实际上二者肯定存在水平偏离。如图3所示，实际拱圈下缘点为C，C'为桥面测点A在拱圈平面上的投影，两点水平偏离为△S。不考虑桥面测点水准测量的误差，则Z坐标的测量误差来源主要有:

(1)棱镜觇板高量测误差:mh可取为±1 mm;

(2)仪器误差:主要由仪器测角、测距误差引起，TCR802全站仪测角误差为±2″，测距误差为±(2+2×10－3S)mm(S的单位为m)，实际测量时，平距S较小，大气折射系数误差可以忽略;

(3)望远镜瞄准觇板上缘和拱圈下缘时的照准误差，可近似取为±2″［5］;

(4)偏离值△S所产生的误差，△S可偏大地取为10 mm。

图3 拱圈下缘高程计算示意图

3.2 Z坐标的测量中误差公式

考虑△S的影响，拱圈下缘点C的高程为:

根据测量误差传播定律［6］可得Z的测量中误差计算公式为:

式(3)中mh为棱镜觇板高量测误差;mS为测距误差;mα、mβ为竖角测量中误差，包含了测角误差和照准误差两项独立误差的影响，取值为±3″;m△S取为±10 mm。

3.3 Z坐标的测量精度分析

假设平距S分别为50 m、100 m、150 m，α分别为70°、75°、80°和 85°，β 分别为 95°、100°、105°和 110°，由式(3)计算Z坐标的测量中误差，结果如表1所示。

由表1可见，当β角不为90°时，由△S引起的误差显著，且β角越偏离90°，此项误差越大，但从理论上来讲，只要使β角为90°，则能消除此项误差;另外，平距S也是影响测量精度的重要因素。因此，为了提高测量精度，应尽量减小△S，并通过合理选择测站位置，减小测程，并使β角尽量接近90°。如此操作，并严格按照测量规范施测，将测量误差控制在5 mm以内，是容易实现的。

Z坐标的测量中误差计算结果 表1

4 工程实例

某2孔16 m净跨实腹式石拱桥，由于山体滑坡，致使一侧桥台向河中心移动，该桥孔主拱圈产生较严重变形，另一孔主拱圈无明显变形和破损，如图4所示。为制定修复方案，采用本文方法实测了拱圈下缘坐标，实测结果采用最小二乘法拟合，得到现状拱圈线形，并与原设计拱圈线形比较得到拱圈竖向变形值。为验证本文方法的精度，将拱顶标高实测值与水准测量值进行了比较，结果如表2所示。

图4 工程实例示意图

由表2可见，采用本文方法测得的拱顶标高与水准测量值相差4 mm，说明本文方法具有较高的精度，能满足工程测量的需要。主拱圈跨中上拱0.197 m，四分点分别下降0.101 m、0.078 m，均远大于L/600，结合裂缝开展情况，将该桥的总体技术状况评定为V类，并对加固与拆除重建两个方案进行了综合比较，最终推荐拆除重建方案。

拱圈下缘Z坐标实测值 表2

5 结论与建议

(1)免棱镜全站仪悬高测量法测定拱圈线形，测量精度高，操作简便，适应性强，是拱圈线形测量的一种较好方法。

(2)点位偏差和测程对测量误差影响显著，因此，精确定出拱圈测点在桥面的投影点，合理选择测站使得β角尽量接近直角，并尽量减小测程，对减小测量误差至关重要。

(3)跨径较大的拱桥，由于车辆荷载作用会产生振动，实测时应尽量避开，同时通过增加测回数、上下游拱圈测量取平均值等方法尽量减小测量误差。

［1］温庆杰，叶见曙.缺失技术资料的旧拱桥现场调查方法研究［J］.公路交通科技，2006，23(4):62～65

［2］钟正强，罗纪彬，彭振斌.拱轴线形激光断面仪的测试方法［J］.中外公路，2009，29(3):126～128

［3］姚冬青，张健雄，李庆勇等.悬高测量方法的再探讨［J］.测绘科学，2008，33(6):92 ～93

［4］夏立福，李井春，胡友健等.免棱镜全站仪测距性能的测试及精度分析［J］.地理空间信息，2008，6(2):133～135

［5］周洪华.关于全站仪照准误差的测试实验与初步分析［J］.辽宁科技学院学报，2007，9(1):15～17

［6］聂让，施锁云，聂泳等.测量学［M］.北京:中国科学技术出版社，2004:128～129