不同载波观测值线性组合对GPS基线解算的影响

李和旺，任超，吴伟

(桂林理工大学土木与建筑工程学院，广西桂林 541004)

1 前言

基线解算是GPS数据处理中的重要环节［1］。基线解算就是一个复杂的平差计算过程，利用GPS接收机接收到的载波相位观测值作为基本观测值，对其进行差分处理，建立观测值与基线向量的关系，通过最小二乘原理求解基线向量及其精度。选取不同的观测值的线性组合进行基线解算对基线解算的结果会有一定的影响，一些学者对载波观测值组合理论进行了研究［3～7］，介绍了多种线性组合，本文通过实验分析探讨其对基线解算结果的影响。

2 载波观测值的线性组合

假设 L1、L2载波的相位观测值分别为 φ1、φ2，则φ1和 φ2之间线性组合的形式［2］为:

式中:n，m为常数。则:组合观测量频率fn，m和波长 λn，m分别为:

式中:f1、f2和 λ1、λ2分别为 L1、L2的频率和波长。

令 N1、N2分别为 φ1、φ2的模糊度，则组合量的模糊度 Nn，m为:

假定 φ1和 φ2的观测噪声不确定，且 σφ1=σφ2=σ，则组合相位的噪声为:

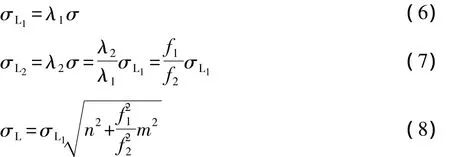
常见的线性组合有:线性组合L1、线性组合L2、消电离层组合Lc、宽巷组合Lw和窄巷组合Ln。

线性组合L1是n=1，m=0时一种特殊形式，线性组合L2是n=0，m=1时的一种形式。

Lc组合称为消电离层组合，它消除了一阶电离层影响，但模糊度不再为整数，且观测噪声比L1放大了3倍，对于短基线(小于15 km)，电离层影响在基线两端有强相关性，即使对站间差分的单频观测，电离层影响也并不显著，用Lc组合非但无益，反而会增加观测噪声，所以Lc组合不宜用于短基线解算。对于中长基线比较有利，因为在这种情况下基线两端的电离层误差已经不相关或弱相关，而且单次差分后残余的电离层延迟误差仍然较大，是影响定位精度的主要误差源，此时采用Lc较合适，可以显著提高中长基线解的精度。

当n=m=1时，组合为宽巷组合 Lw，其波长0.86 m，且模糊度为整数，电离层延迟及观测值噪声也不大，可以加速模糊度的固定，用于中长基线的模糊度的分解。

当n=1，m=－1时，组合为窄巷组合Ln，其波长为0.107 m，且模糊度也为整数，它的观测值噪声最小，常用于短基线高精度GPS定位。Lw组合和Ln组合中电离层影响的大小相等，符号相反。

3 实例分析

为了说明不同载波观测值的线性组合对基线解算结果的影响，选取了某GPS控制网的3条不同长度的基线。利用南方测绘GPS 4.4数据处理软件，分别采取 L1、L2、Lc、Lw、Ln，5 种数据处理中常用线性组合，截取3 h的观测数据进行基线解算。采用不同组合时，各基线分量的中误差及由分量中误差计算的长度中误差，结果如表1所示。

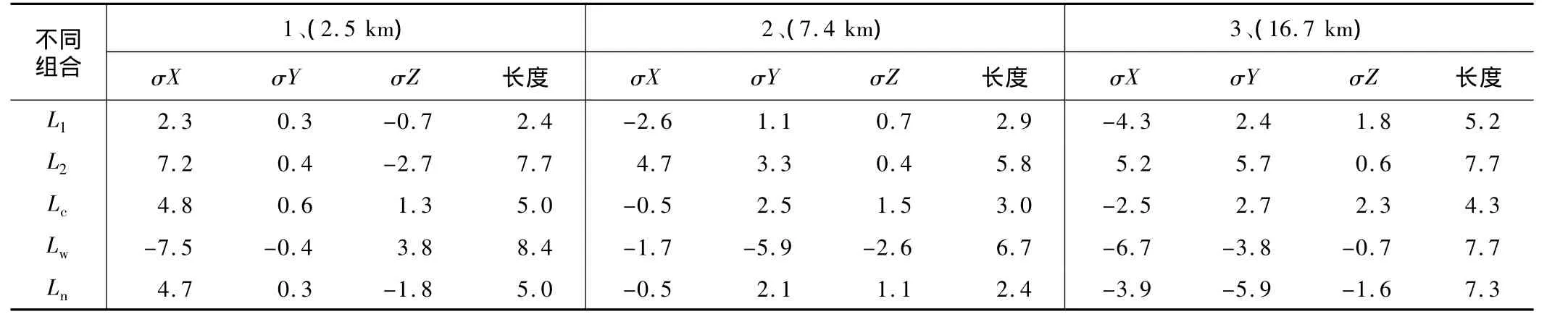
不同观测值组合对基线解算精度的影响(单位/mm) 表1

由表1可以看出:

(1)采用Lc组合进行基线解算的精度优于采用L2线性组合进行解算的精度。

(2)对于相对较短的基线，采用L1线性组合就可以达到较好的精度，采用电离层消除模型反而降低了基线的精度。

(3)随着基线长度的增加，加入电离层改正的必要性增强。

4 结语

通过上述研究，对于长基线可采用消电离层组合模式进行基线解算，解算结果能够得到明显的改善。对于短基线来说，经差分处理后电离层的影响不占主导地位，过分地考虑电离层影响是没有必要的。在GPS基线解算中，选择不同的线性组合对基线精度有一定的影响，在实际应用中，应根据具体的基线情况选择合适的线性组合进行解算，从而能够得到满意的结果。

［1］边少锋.卫星导航系统概论［M］.北京:测绘出版社，2004

［2］魏子卿，葛茂荣.GPS相对定位的数学模型［M］.北京:测绘出版社，1998

［3］常青，柳重堪，张其善.GPS载波相位组合观测值理论研究［J］.航空学报，1998，5(19):612～616

［4］韩绍伟.GPS组合观测值理论及应用［J］.测绘学报，1995，2(21):8 ～13

［5］WU Yue，PAN Yong，FAN Yimin，WANG Xiaojun.Positioning Precision Analysis of GNSS Multi－frequency Carrier Phase Combinations［J］，Geo－spatial Information Science，2007，10(4):245 ～249

［6］YI Bing－xin，HUANG Yong－bo，LIN Gang－chui.Model of combined observations of Galileo and GPS carrier phase［J］.Journal of Chinese Inertial Technology，2008，1(16):58 ～63

［7］陈明剑，郝金明，周凤歧.多频载波相位组合进行单点定位［J］.测绘科学技术学报，2008，25(2):94～97