基于Fluent的孔式静压径向气体轴承承载性能分析

李国芹，吕胜宾，张鹏程

(1.河北工程技术高等专科学校，河北 沧州 061001；2.北京科技大学，北京 100083；3.河北省南运河河务管理处，河北 沧州 061001)

气体轴承具有高速度、高旋转精度、零磨损和长寿命的优点，为了满足高转速、高精度机床的需求，研究气体轴承具有重要意义。静压气体轴承在工程中应用广泛，但其设计工作涉及的计算繁琐，工程中多采用图表法或数值计算法。在求解气体的压力场时，由于轴承间隙中的气体流动是一种极其复杂的三维流动，使用图表法或数值计算法分析气体的压力分布情况和求解压力的大小极其困难，再加上计算过程要做一些假设条件，从而带来一些误差。Fluent软件是一个用来模拟从不可压缩到高度可压缩范围内复杂流动的专用CFD软件[1]，利用其可以更加准确地分析预测出气体流动实际的细节情况，如速度场、压力场、温度场、密度场的分布随时间变化的特性，并且可得到一些规律性的结论。另外传统的设计方法对试验和经验的依赖性大，设计周期长，导致成本较高[2]，而利用Fluent软件作流体分析不需要编程计算，能够节约大量设计时间，缩短设计周期，大大提高工作效率，降低成本。采用Fluent软件对静压气体轴承的承载性能进行准确的计算分析，既简化了工程计算过程，也为研究气体轴承中各参数间的关系提供了直观的分析依据，使产品或工程设计对试验和经验的依赖性大大减小，是一种比较理想的分析设计手段。

1 Fluent软件

Fluent是用于计算流体流动和传热问题的程序，其提供的非结构网格生成程序对相对复杂的几何结构网格生成非常有效。可生成的网格包括二维的三角形和四边形网格，三维的四面体、六面体及混合网格。Fluent还可根据计算结果调整网格，这种网格的自适应能力对于精确求解有较大梯度的流场有实际作用。由于网格自适应和调整只是在需要加密的流动区域里实施，而非整个流场[1]，因此可以节约计算时间。 Fluent程序软件由前处理器GAMBIT、求解器和后处理器3大模块组成。GAMBIT作为专用的前处理软件，具有超强组合建构模型的能力和强大的网格生成能力，支持界面不连续网格、混合网格、动网格以及滑动网格等，还拥有多种基于解的网格的自适应、动态自适应技术以及动网格与网格动态自适应相结合的技术，这对解决各种复杂外形的流动非常有效；其还具有丰富的CAD 接口，可以读入PRO /E，UG，AUTOCAD等多种软件的三维几何模型和ANSYS等多种CAE软件的网格模型[1]。Fluent软件的求解模块是其核心部分，该模块能推出多种优化的物理模型，如定常和非定常流动、层流、紊流、不可压缩和可压缩流动、传热、化学反应等等。针对各种复杂的流动和物理现象，采用不同的离散格式和数值方法，以期在特定的领域内使计算速度、稳定性和精度等方面达到最佳组合，从而高效解决各个领域的复杂流动计算问题。Fluent软件自带的专用图形后处理模块能够显示流场分析中用到的各种图形及曲线，如速度矢量图、等值线图(流线图、等压线图等)、等值面云图(等温面、等Ma数面等)、迹线图、XY-PLOT功能、体积(或面积)积分功能(力、流量等)、用户定义量的显示、残差和计算值的监控等[3]。

2 孔式静压径向气体轴承的结构

所分析轴承具体的结构尺寸参数见表1，具体的结构如图1所示。

表1 静压径向气体轴承结构尺寸

图1 静压径向气体轴承结构图

3 轴承承载性能的数值分析

3.1 孔式静压径向气体轴承模型建立

气体在轴承间隙内流动实际上是三维的非常复杂的运动过程，其精确模型的求解在大多数情况下几乎是不可能的。因此为了简化计算，引用如下假设[4]：

(l)润滑气体为Newton流体，气体黏性系数为常数；

(2)轴承间隙内的气流是层流状态，且流向一致；

(3)在垂直于气膜厚度方向上，速度变化可以忽略，即压力沿膜厚方向无变化；

(4)气流的惯性力与黏性力相比忽略不计；

(5)气膜的质量忽略不计；

(6)气流在轴和轴承表面不存在相对滑动。

分析轴承的承载性能[5-8]，就是主要分析轴承表面压力分布情况和气膜承载力的大小，因此将从节流小孔处到轴承间隙间的流动气体作为主要研究对象，建立三维模型，如图2所示。气膜上的每一点压力的合力就是轴承的承载力W，如果忽略轴的重力，当轴上无载荷时，轴与轴承的中心重合，气膜区的形状是一个厚度均匀的薄壁圆筒，气膜平均厚度为h0，当轴受到某一方向的载荷时，轴将沿载荷方向偏离中心位置，偏心量为e，轴的偏移会引起气膜厚度的变化，导致气膜上压力分布也随之变化。用偏心量e与气膜平均厚度h0的比值定义偏心率ε，即ε=e/h0。

图2 轴承完整结构图

又考虑到轴承的结构具有几何对称性，为了减少网格数目和计算量，选择整个模型的1/4区域的气体作为模拟分析研究对象。

3.2 模型网格化和施加边界条件

由于轴承的供气孔与节流孔连接处孔的横截面发生突变，节流孔的横截面积比供气孔的横截面积小得多，高压气体流经这里时，流速急剧增加，导致速度梯度和压力梯度均变得很大，因此在划分网格时，此处网格密度要相应很高[9]，网格划分如图3所示。然后通过如图4所示的边界条件面板设定所有的边界条件，由于仿真研究对象取整个模型的1/4，因此需施加2个几何平面对称条件，即xOy对称面和xOz对称面；于供气孔、节流孔、轴承接触的气膜表面，施加零速度边界条件，由于轴承固定，研究轴承的静态性能时轴相对轴承没有转动或转动速度较低。还有2个压力边界条件：轴承的端部直接排入大气，出口处的压力即环境压力P0=0，因此，轴承端部气膜表面需加零压力边界条件；供气孔端面的供气压力PS=0.6 MPa为已知条件，因此供气孔端面处的气膜表面加0.6 MPa的压力边界条件。边界条件示意图如图5所示。

图3 轴承网格划分图

图4 边界条件的面板

图5 边界条件示意图

3.3 Fluent数值模拟的结果

3.3.1 气膜压力场分布

节流孔数为8，气膜平均厚度为0.021 mm，取不同的偏心率值进行计算分析，采用图中的坐标系，轴在承载力的作用下向+x方向偏移，观察仿真图的方向由-y向+y方向观察。

由图6可知：当偏心率ε=0时，气场中节流孔位置处压力最高，而轴承端部气体排放口位置处压力最低，为环境压力。整个气膜上的压力分布呈几何对称性，且轴承间隙中的气膜薄厚均匀；随着偏心率的逐渐增大，即轴承承载力沿+x方向不断增加，气膜的厚度不再均匀，气膜左边区域的厚度越来越薄，右边区域的厚度越来越厚，气膜上的压力分布也随之变化，在气膜越薄的区域压力越大，气膜变厚的区域压力变小。偏心率越大，即承载力越大，左、右两边气膜的厚度差越大，高低压力趋于集中而形成较大的压力差，以平衡外载荷的增加，从而提高轴承承载力。

图6 气膜上的压力分布

3.3.2 轴承的承载特性

承载能力随偏心率的变化如图7、图8所示。总体而言，随着偏心率的增大，轴承的承载力也随之增大，但增长的规律不呈线性关系。当偏心率较小(0.1～0.3)时，承载力随着偏心率的增大而增长得比较明显；当偏心率趋向极限值时，即轴与轴套将要处于接触状态时，承载力随偏心率变化增长趋于缓慢。

节流孔数不变，将气膜平均厚度变为0.015 mm和0.025 mm，分别仿真分析轴承承载力随偏心率的变化而变化的关系。由图7可知，承载力随着气膜平均厚度的增大而减小，随着偏心率的增大，气膜平均厚度大的轴承承载力增大的速度较缓慢。

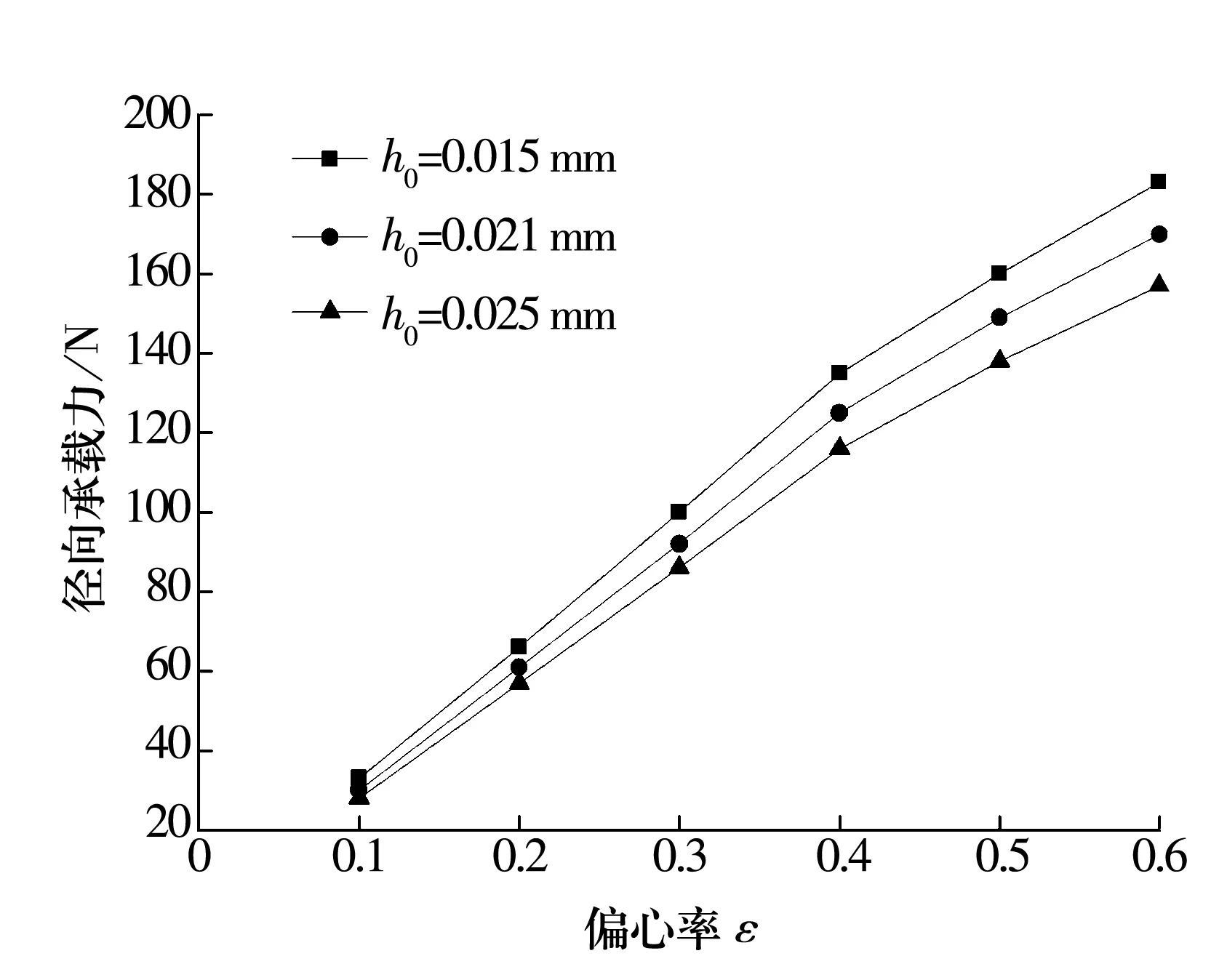
图7 不同气膜厚度时轴承承载力与偏心率的关系

图8 不同节流孔数时轴承承载力与偏心率的关系

轴承间隙的气膜平均厚度不变，将节流孔数变为6，再仿真分析轴承承载力随偏心率的变化关系。由图8可知，承载力随着轴承节流孔数的减少而减小；随着偏心率的增大，节流孔数少的轴承承载力增大的速度较缓慢。

4 结论

(1)应用Fluent数值模拟可以很方便地处理节流小孔进入到气膜内区域的复杂流场流动，易于分析轴承在不同偏心率下气膜上的压力分布。

(2)随着偏心率增大，轴承的承载力也随之增大，但承载力随偏心率的增大不呈线性规律。当偏心率趋于极限值时，即轴与轴套将要接触时，随偏心率的增大，承载力的增大速度变得缓慢。

(3)轴承的承载力随着气膜平均厚度的增大而减小。