基于相空间的滚动轴承振动特征参数的乏信息分析
高磊磊,夏新涛,樊雎,孙小超
(河南科技大学 机电工程学院,河南 洛阳 471003)
滚动轴承的振动水平是轴承动态性能质量的重要反映[1],因此一直受到相关工程与学术界的重视。文献[2-3]基于轴承振动信号数据分别用时域特征和神经网络法进行轴承故障的诊断处理。文献[4]对轴承振动信号数据进行光谱分析等处理并用于轴承的故障诊断。文献[5]用灰自助法对轴承振动数据进行了动态评估与诊断。文献[6]提出了基于Hilbert-Huang变换的轴承振动特性分析的新方法。现有的研究大多尚未关注乏信息系统领域。乏信息是指研究对象所表现出的属性特征信息不完整与不充分。乏信息系统的参数估计,目前是信息科学与系统科学领域的前沿与热点之一,具有重要的理论意义和实用价值。
乏信息系统的相空间重构理论是分析研究非线性动力系统的基础,相空间是描述系统演化与运动最有力的工具。用混沌理论进行相空间重构,能使轴承振动时间序列的原始动力学特征得到最优恢复。
研究表明,轴承振动具有不确定的明显波动和趋势变化,属于概率分布和趋势规律都未知的乏信息系统。下文基于乏信息相空间,用最大熵自助法[7-8]分别建立当前样本和先验样本的概率密度函数,然后结合Bayes统计理论,建立轴承振动特征参数的动态Bayes后验概率密度函数,最后对特征参数进行点估计、区间估计及趋势估计等,从而为轴承性能的非线性动力学特征演变评估奠定新的理论基础。
1 乏信息数学模型
针对轴承振动特征参数的评估,用乏信息系统理论进行相空间重构,并结合最大熵自助法和Bayes统计理论构建数学模型进行参数估计。
1.1 相空间重构
设轴承振动信号的时间序列为
X=(x(1),x(2),…,x(k),…,x(N));k=1,2,…,N;
(1)
式中:x(k)为第k个数据;N为时间序列X中数据的个数。
重构相空间[9],得到一组新的向量序列
X(t)=(x(t),x(t+τ),…,x(t+(k-1)τ),…,x(t+(m-1)τ));t=1,2,…,M;k=1,2,…,m;
(2)
M=N-(m-1)τ;
(3)
式中:x(t)为t时刻的观测值;x(t+(m-1)τ)为延迟值;m为嵌入维数;τ为延迟时间;M为相点个数。
(1)式是由观测值x(t)和延迟值x(t+(m-1)τ)所构成的m维乏信息相空间,其与原始的状态空间微分同构。
至此,乏信息过程的原始动力学特征得到最优恢复。选定当前时刻t,将此刻的相轨迹作为中心轨迹。从当前时刻t往前隔(τ-1)个数据取一个,得到一个含有m个数据的样本X1,即为基于中心轨迹的当前样本。先验样本就是当前时刻t以前的历史轨迹,从时刻(t-1)往前隔(τ-1)个数据取一个,得到一个含有m个数据的样本。让t依次往前滚动递减,重复以上步骤,即可得到多个含有m个数据的样本序列Xi。
借鉴混沌预测的思想,从样本序列Xi中找出与当前样本X1最相似的样本X2,即为基于历史轨迹的先验样本。因为样本序列Xi中很多样本信息对于当前时刻的参数估计已经没有太大价值,应予以剔除。用2-范数法来确定Xi与X1的相似度,
(4)
式中:xij为Xi的第j个元素;x1j为X1的第j个元素。
通过计算,找出(4)式值最小的样本,即为先验样本X2。
由于样本X1和X2中数据较少,还须用自助法抽样,以便建立基于当前样本和先验样本的最大熵概率密度函数。
1.2 自助样本
从X中等概率可放回地抽样,抽取m个数据,得到一个样本Xb,共抽取B次,得到B个自助样本,
Xb=(xb(1),xb(2),…,xb(k),…,xb(m));b=1,2,…,B;
(5)
式中:Xb为第b个自助样本;xb(k)为第b个自助样本的第k个数据,k=1,2,…,m。
求自助样本Xb的均值为
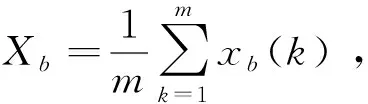
(6)
从而得到一个样本含量为B的自助样本
XBootstrap=(X1,X2,…,Xb,…,XB)。
(7)
用自助法[10]分别对当前样本X1和先验样本X2进行抽样处理,得到当前自助样本X1Bootstrap和先验自助样本X2Bootstrap。
1.3 最大熵概率密度函数
根据最大熵原理,最无主观偏见的概率密度函数应满足熵最大,即
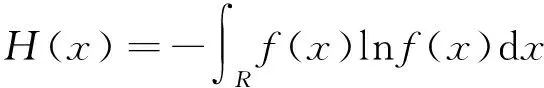
(8)
式中:R为积分空间。约束条件为各阶原点距,
(9)
式中:k为原点距数;wk为第k阶原点距;w为所用到的最高价原点距的阶次,一般w=3~8,常用w=5。
在约束条件下调节f(x)可使熵最大,这是约束优化问题,用Lagrange乘子法可求出f(x)的表达式,
(10)
式中:ck为第k个Lagrange乘子,k=1,2,…,w。第1个Lagrange乘子c0为
(11)
其他w个乘子满足
(12)
将上式用向量表示为
G=G(c)=(gk;k=1,2,…,w)T=0,
(13)
且有
c=(ck;k=1,2,…,w)T,
(14)
式中:c为Lagrange乘子列向量。可用Newton法求解Lagrange乘子向量c,即有
cj+1=cj-G′(cj)-1G(cj) (j=0,1,…) ,
(15)
式中:G′(cj)为迭代到第j步的Jacobi矩阵。迭代收敛的范数准则为
‖Gj+1-Gj‖1≤ε,
(16)
式中:ε为收敛误差,一般取ε=10-12。
上述求解中,第k阶原点距由前面得到的自助样本XBootstrap确定。
用最大熵法分别对当前自助样本X1Bootstrap和先验自助样本X2Bootstrap进行处理,得到当前样本的最大熵概率密度函数f1(x)和先验样本的最大熵概率密度函数f2(x)。最后再结合Bayes统计理论,得到基于相空间的轴承振动特征参数的Bayes后验概率密度函数。
1.4 Bayes概率密度函数
Bayes统计[11]认为,任何一个未知量θ都可以看成随机变量,应用一个概率分布去描述对θ的未知状况。这个概率分布是在抽样前就有的关于θ的先验信息的概率陈述,其称为先验分布。为了在小子样下获得好的参数估计,就必须利用参数的历史资料即先验信息。Bayes统计认为,后验分布综合了先验和样本的信息,可对参数做出较先验分布更合理的估计。
Bayes公式的概率密度函数形式为
(17)
式中:θ为统计推断参数;Θ为参数空间,Θ={θ};x为总体分布产生的一个样本,x=(x1,x2,…,xn);f(θ|x)为在样本x给定下θ的条件分布,即后验分布;h(x|θ)为总体指标X的条件分布;f(θ)为先验分布。
根据当前样本的概率密度函数f1(x)和先验样本的概率密度函数f2(x),再结合Bayes统计原理,得出Bayes后验概率密度函数为
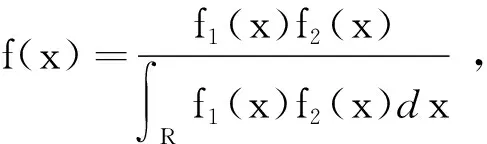
(18)
式中:x为样本均值。
2 特征参数估计
基于Bayes概率密度函数进行参数估计。
估计真值X0为
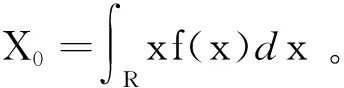
(19)
设显著水平α∈[0,1],估计区间的下边界值XL应满足
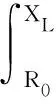
(20)
上边界值Xu应满足
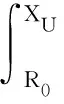
(21)
于是,在置信水平P=(1-α)×100%下,样本均值的估计区间为[XL,XU]。
3 试验研究与讨论
采用美国Case Western Reserve University电气工程实验室的轴承故障模拟试验台的试验数据进行研究分析。选取驱动端转速为1 796 r/min,采样频率为12 kHz时得到的钢球故障数据时间序列进行验证,其中损伤直径为0.1 778 mm。取数据文件里的前1 000个数据作为时间序列进行建模处理。
在计算最大熵概率密度函数时,取w=5,Q=9,ε=10-12,数据的时域信息及利用乏信息数学模型估计得到的结果如图1和图2所示。在计算特征参数时,取α=0.05,B=10 000,图2中选定当前时刻t为1 000个振动数据的第732个,每计算一次让t自动加1,连续计算10次,将估计结果绘制成图像。
由图1可知,在测量过程中,随着轴承的转动(原始数据序列号 从1增加到1000),轴承振动的时域信息具有明显的随机波动和趋势变化特征,可见轴承振动的时域信息很复杂。
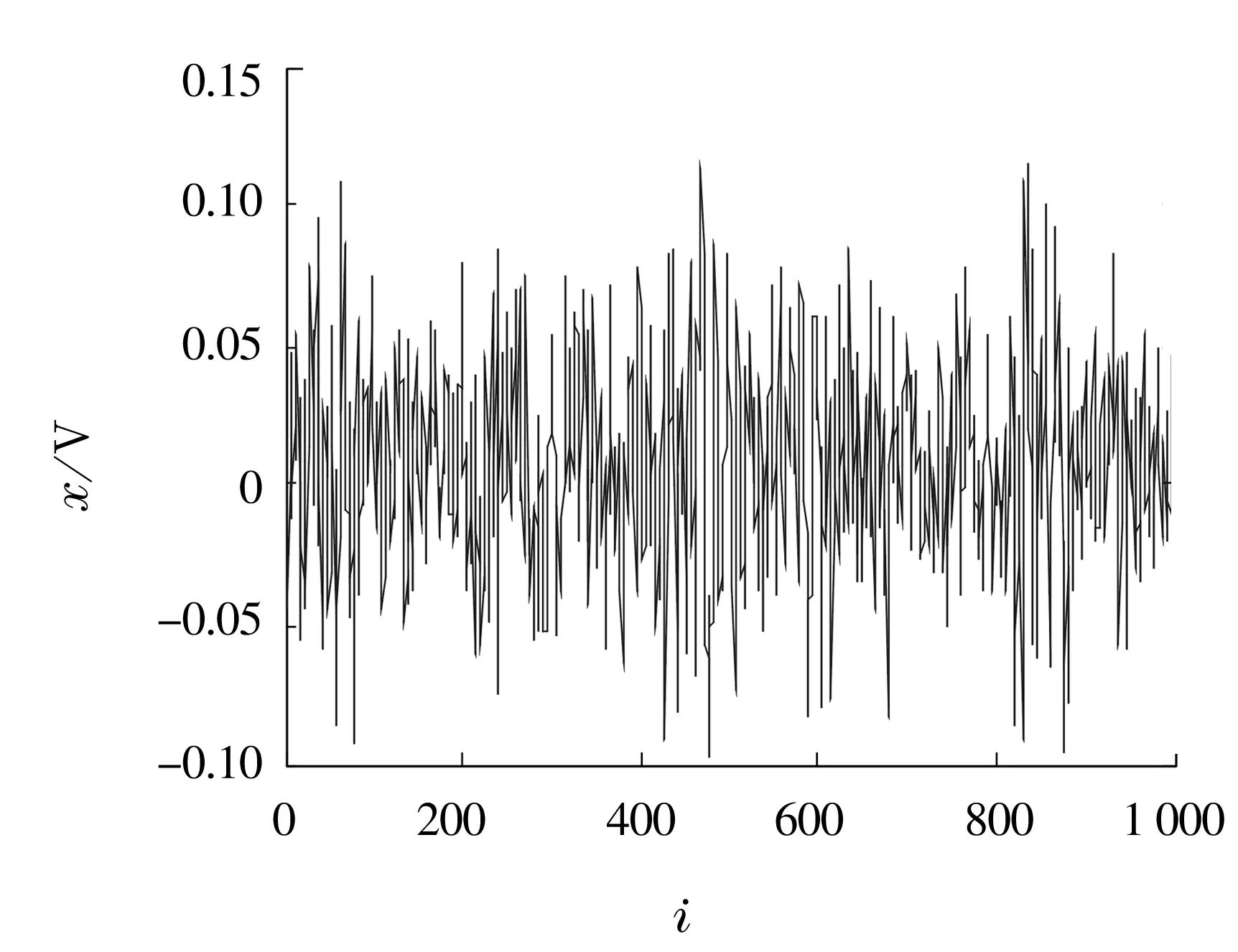
图1 轴承振动数据
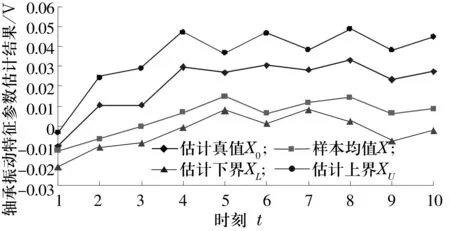
图2 估计区间对样本均值的包络
由t=1~10各时刻的Bayes概率密度函数可知,从t=1~10,轴承振动的Bayes概率密度函数处于不断变化之中,其中t=3时概率密度函数近似于正态分布,其余时刻概率密度函数呈现非对称的单峰形或多峰形(图3),这是随机过程短期的多次实现的结果,可见轴承振动的概率分布信息非常复杂且具有不确定性。这些复杂信息实际上隐含着系统真值的一些特征。
根据图2所示,轴承振动数据的样本均值序列X被完美地包络在估计区间[XL,XU]之中,且估计真值X0与样本均值X非常接近。可以看出,t=1时估计真值X0与样本均值X之间的绝对误差小到0.002 5;t=6时估计真值X0与样本均值X之间的绝对误差最大为0.024 0。这说明利用乏信息数学模型处理振动数据能得到比较合理的结果。因此,估计结果的误差可以满足工程要求。这也证实了所提出的数学模型是合理与可行的,基本上可以真实描述轴承振动的统计特征。
4 结论
相空间是描述系统演化与运动最有力的工具。用混沌理论进行相空间重构,使轴承振动时间序列的原始动力学特征得到最优恢复。在相空间里,建立了基于最大熵自助法和Bayes统计理论的轴承振动的动态Bayes后验概率密度函数。轴承振动的Bayes概率密度函数呈非对称的单峰形或多峰形,这是随机过程短期的多次实现的结果。这刻画了轴承振动不确定的明显波动和趋势变化特征。
以Bayes概率分布函数为基础,提出了轴承振动特征参数的真值估计、区间估计和趋势估计方法。从计算结果来看,轴承振动数据的样本均值都能被估计区间完美地包络,且估计结果和试验结果在数值上很接近,满足工程要求。从而为轴承性能的非线性动力学特征演变评估奠定新的理论基础。
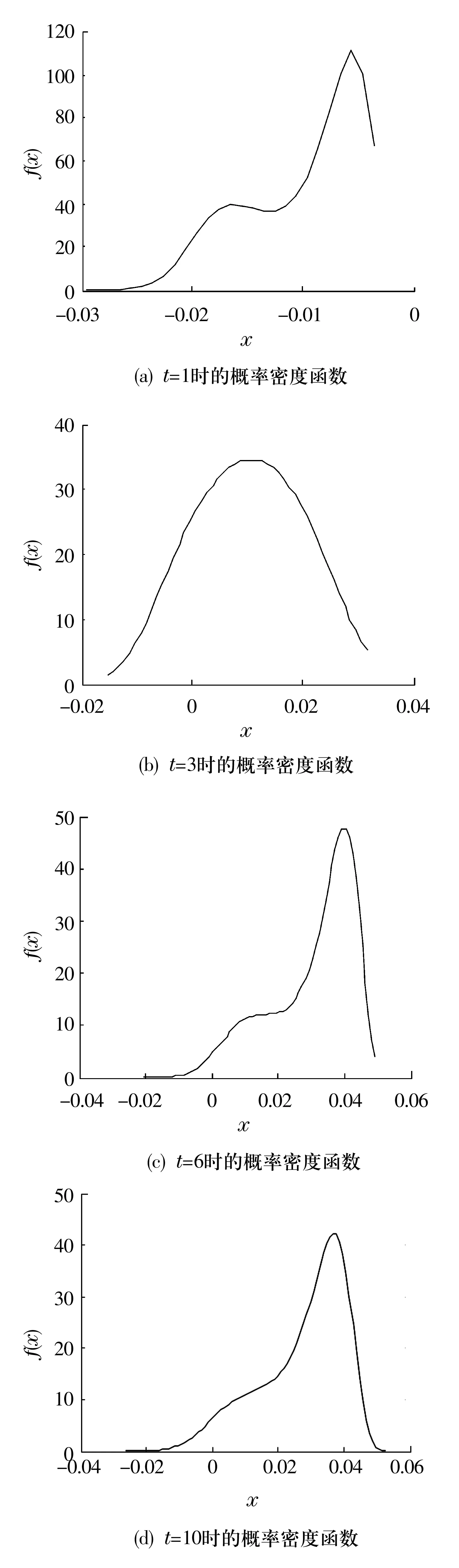
图3 t=1,3,6,10时刻的概率密度函数

